2023-2024学年广东省广州市南沙区八年级(下)期末数学试卷(含答案)
文档属性
| 名称 | 2023-2024学年广东省广州市南沙区八年级(下)期末数学试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 97.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-15 16:09:50 | ||
图片预览




文档简介
2023-2024学年广东省广州市南沙区八年级(下)期末数学试卷
一、选择题:本题共10小题,每小题3分,共30分。在每小题给出的选项中,只有一项是符合题目要求的。
1.下列二次根式中是最简二次根式的是( )
A. B. C. D.
2.一组数据,,,,,,的众数是( )
A. B. C. D.
3.在平行四边形中,,则的度数是( )
A. B. C. D.
4.下列计算正确的是( )
A. B. C. D.
5.在平面直角坐标系中,点,在函数的图象上,则( )
A. B. C. D. 无法判断
6.如图,四边形是平行四边形,,是两条对角线,添加下列条件后能判定四边形是矩形的是( )
A.
B.
C.
D. 平分
7.在中,,,所对的边分别为,,,下列选项中能判定是直角三角形的是( )
A. :::: B. ,,
C. D.
8.已知小丽家、便利店、体育馆在同一直线上,某天小丽从家步行到便利店买了一瓶水,再到体育馆锻炼,最后骑共享单车回家小丽离家距离与时间之间的关系如图所示下列结论错误的是( )
A. 小丽家到便利店距离米
B. 小丽在便利店停留了分钟
C. 小丽步行的速度是
D. 小丽骑自行车的速度是步行速度的倍
9.如图,在 中,对角线与相交于点,是边中点,连接若的长为,的周长为,则的周长是( )
A. B. C. D.
10.如图,在矩形中,点在上,,,作于点,交于,则的长是( )
A.
B.
C.
D.
二、填空题:本题共6小题,每小题3分,共18分。
11.若二次根式在实数范围内有意义,则的取值范围为______.
12.技术员分别从甲、乙两块玉米试验田中随机抽取株玉米苗,测得玉米苗高的平均数相同,方差分别为,,则玉米苗长得更整齐的试验田是______.
13.若直线与轴的交点为,则关于的一元一次方程的解为______.
14.如图,在中,,,点是的中点,,则的度数为______.
15.如图,某港口在南北方向的海岸线上,快、慢两艘船同时离开港口,各自沿一固定方向航行,已知快、慢两船每小时分别航行海里和海里,小时后两船分别位于点,处,且相距海里,如果知道快船沿北偏西方向航行,那么慢船沿______方向航行.
16.如图,一次函数的图象与轴、轴分别交于点和点,点的坐标为,点,分别是线段,上的动点,且,则的长为______;当的值取最小值时,点的坐标为______.
三、解答题:本题共9小题,共72分。解答应写出文字说明,证明过程或演算步骤。
17.本小题分
计算:.
18.本小题分
如图,在中,,,,以点为圆心,长为半径画弧交于点,求的长.
19.本小题分
如图,、为 的对角线上的两点,请你添加一个条件,使得.
你添加的条件是______.
根据你添加的条件和题目的已知条件,求证:.
20.本小题分
小明打算利用暑假阅读名著儒林外史,该书有页,他计划每天看页,设小明看书时间为天,还剩下页书没看.
求与的函数关系.
当小明阅读天后,还剩下多少页书没看.
21.本小题分
年月日,神舟十八号载人飞船发射取得成功,将我国航天事业推向了新的高峰南沙区某中学为了丰富学生们航天知识,组织全校学生进行航天知识竞赛,并随机抽取名学生的成绩,整理成如统计表:
分数
频数
该名同学这次竞赛成绩的中位数是______.
求该名同学这次竞赛成绩的平均数.
若竞赛成绩分以上含分为优秀,该校有名学生,请估计竞赛成绩为优秀的人数.
22.本小题分
已知一次函数的图象不经过第四象限.
求的取值范围.
当时,在给定的平面直角坐标系中画出该函数的图象.
在的情况下,当时,根据图象求出的取值范围.
23.本小题分
在进行二次根式化简时,我们有时会碰上形如的式子,这样的式子我们可以将其进一步化简,,,这种化简的方法叫做分母有理化,请利用分母有理化解答下列问题:
化简; ______. ______.
矩形的面积为,一边长为,求这个矩形的周长.
当时,化简:.
24.本小题分
如图,矩形的一边在轴上,点的坐标为,点的坐标为.
求证:四边形为正方形;
如图,若点为中点,连接,,直线交于点,交轴于点.
求的面积.
点在轴的正半轴上,平面内是否存在点,使以点,,为顶点的四边形是菱形?若存在,请求出点的坐标;若不存在,请说明理由.
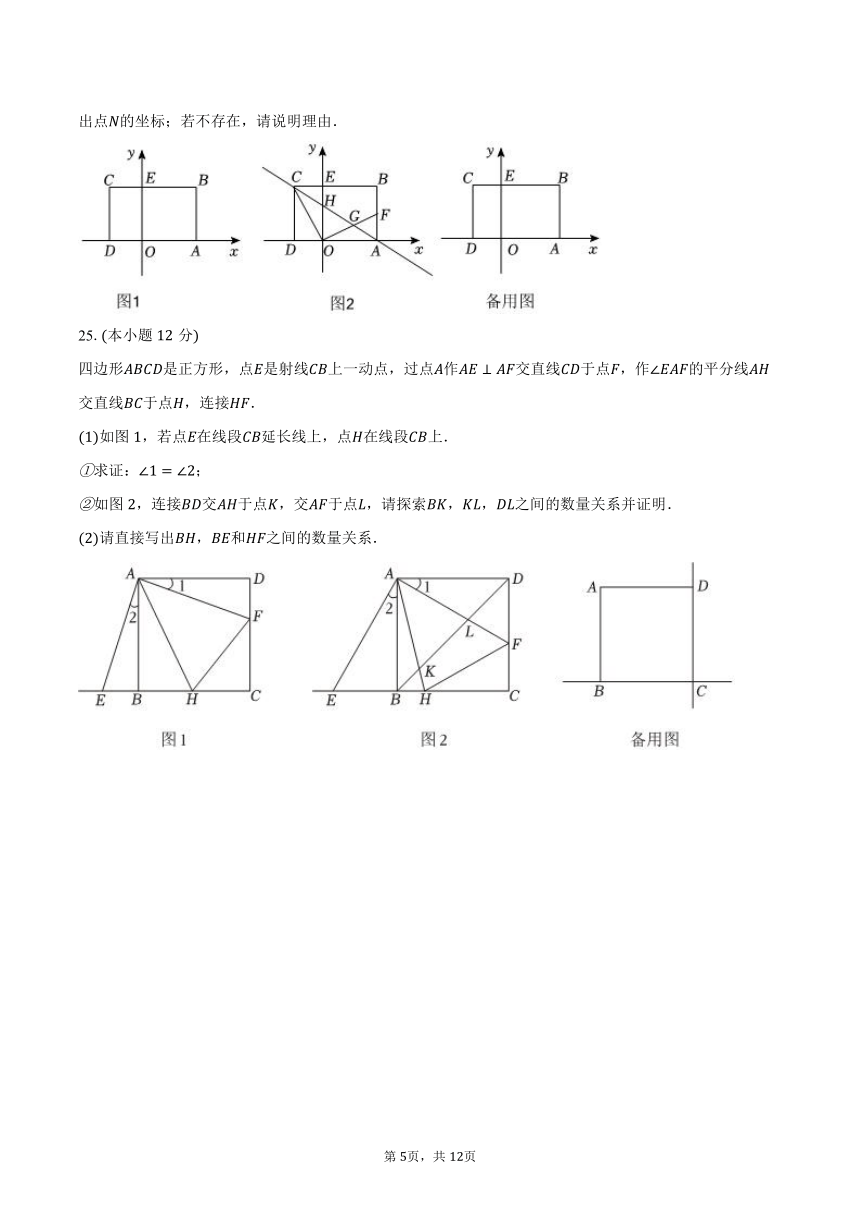
25.本小题分
四边形是正方形,点是射线上一动点,过点作交直线于点,作的平分线交直线于点,连接.
如图,若点在线段延长线上,点在线段上.
求证:;
如图,连接交于点,交于点,请探索,,之间的数量关系并证明.
请直接写出,和之间的数量关系.
参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.甲
13.
14.
15.南偏西
16.
17.解:原式
.
18.解:在中,,,
,
以点为圆心,长为半径画弧,交于点,
,
.
19.答案不唯一;
证明:四边形是平行四边形,
,,
,
在和中,
,
≌,
.
20.解:与的函数关系式:;
时,
页,
当小明阅读天后,还剩下页书没看.
21.;
该名同学这次竞赛成绩的平均数为;
名,
答:估计竞赛成绩为优秀的人数为名.
22.解:一次函数的图象不经过第四象限,
,
解得;
当时,
,
当时,,当时,,
该一次函数的图象如图所示:
由图象可得,当时,的取值范围是.
23.,;
另一边长为:,
所以,
答:这个矩形的周长为;
当时,
.
24.证明:,
,
四边形是矩形,
,
,
四边形是矩形,
,
,
,
,
四边形为正方形;
解:由知,,四边形为正方形,
,
点为中点,
,
由,的直线解析式为,
由,得直线解析式为,
联立,解得,
,
在中,令得,
,
,
,,
,
的面积为;
平面内存在点,使以点,,为顶点的四边形是菱形,理由如下:
设,,
而,,
当,为对角线时,,的中点重合,且,
,
解得,
;
当,为对角线时,,的中点重合,且,
,
解得或此时不在轴正半轴,舍去,
;
当,为对角线时,,的中点重合,且,
,
解得或舍去,
;
综上所述,的坐标为或或
25.证明:四边形是正方形,
,即,
,
,即,
;
解:,证明如下:
在上取点,使,连接,,如图:
在和中,
,
≌,
,,
四边形是正方形,
,
,
,
,
平分,
,
,,
≌,
,
;
解:当在线段延长线上时,如图:
,,,
≌,
,
,,
≌,
,
;
当在线段上时,如图:
,,,
≌,
,
,,
≌,
,
;
综上所述,当在线段延长线上时,;当在线段上时,.
第1页,共1页
一、选择题:本题共10小题,每小题3分,共30分。在每小题给出的选项中,只有一项是符合题目要求的。
1.下列二次根式中是最简二次根式的是( )
A. B. C. D.
2.一组数据,,,,,,的众数是( )
A. B. C. D.
3.在平行四边形中,,则的度数是( )
A. B. C. D.
4.下列计算正确的是( )
A. B. C. D.
5.在平面直角坐标系中,点,在函数的图象上,则( )
A. B. C. D. 无法判断
6.如图,四边形是平行四边形,,是两条对角线,添加下列条件后能判定四边形是矩形的是( )
A.
B.
C.
D. 平分
7.在中,,,所对的边分别为,,,下列选项中能判定是直角三角形的是( )
A. :::: B. ,,
C. D.
8.已知小丽家、便利店、体育馆在同一直线上,某天小丽从家步行到便利店买了一瓶水,再到体育馆锻炼,最后骑共享单车回家小丽离家距离与时间之间的关系如图所示下列结论错误的是( )
A. 小丽家到便利店距离米
B. 小丽在便利店停留了分钟
C. 小丽步行的速度是
D. 小丽骑自行车的速度是步行速度的倍
9.如图,在 中,对角线与相交于点,是边中点,连接若的长为,的周长为,则的周长是( )
A. B. C. D.
10.如图,在矩形中,点在上,,,作于点,交于,则的长是( )
A.
B.
C.
D.
二、填空题:本题共6小题,每小题3分,共18分。
11.若二次根式在实数范围内有意义,则的取值范围为______.
12.技术员分别从甲、乙两块玉米试验田中随机抽取株玉米苗,测得玉米苗高的平均数相同,方差分别为,,则玉米苗长得更整齐的试验田是______.
13.若直线与轴的交点为,则关于的一元一次方程的解为______.
14.如图,在中,,,点是的中点,,则的度数为______.
15.如图,某港口在南北方向的海岸线上,快、慢两艘船同时离开港口,各自沿一固定方向航行,已知快、慢两船每小时分别航行海里和海里,小时后两船分别位于点,处,且相距海里,如果知道快船沿北偏西方向航行,那么慢船沿______方向航行.
16.如图,一次函数的图象与轴、轴分别交于点和点,点的坐标为,点,分别是线段,上的动点,且,则的长为______;当的值取最小值时,点的坐标为______.
三、解答题:本题共9小题,共72分。解答应写出文字说明,证明过程或演算步骤。
17.本小题分
计算:.
18.本小题分
如图,在中,,,,以点为圆心,长为半径画弧交于点,求的长.
19.本小题分
如图,、为 的对角线上的两点,请你添加一个条件,使得.
你添加的条件是______.
根据你添加的条件和题目的已知条件,求证:.
20.本小题分
小明打算利用暑假阅读名著儒林外史,该书有页,他计划每天看页,设小明看书时间为天,还剩下页书没看.
求与的函数关系.
当小明阅读天后,还剩下多少页书没看.
21.本小题分
年月日,神舟十八号载人飞船发射取得成功,将我国航天事业推向了新的高峰南沙区某中学为了丰富学生们航天知识,组织全校学生进行航天知识竞赛,并随机抽取名学生的成绩,整理成如统计表:
分数
频数
该名同学这次竞赛成绩的中位数是______.
求该名同学这次竞赛成绩的平均数.
若竞赛成绩分以上含分为优秀,该校有名学生,请估计竞赛成绩为优秀的人数.
22.本小题分
已知一次函数的图象不经过第四象限.
求的取值范围.
当时,在给定的平面直角坐标系中画出该函数的图象.
在的情况下,当时,根据图象求出的取值范围.
23.本小题分
在进行二次根式化简时,我们有时会碰上形如的式子,这样的式子我们可以将其进一步化简,,,这种化简的方法叫做分母有理化,请利用分母有理化解答下列问题:
化简; ______. ______.
矩形的面积为,一边长为,求这个矩形的周长.
当时,化简:.
24.本小题分
如图,矩形的一边在轴上,点的坐标为,点的坐标为.
求证:四边形为正方形;
如图,若点为中点,连接,,直线交于点,交轴于点.
求的面积.
点在轴的正半轴上,平面内是否存在点,使以点,,为顶点的四边形是菱形?若存在,请求出点的坐标;若不存在,请说明理由.
25.本小题分
四边形是正方形,点是射线上一动点,过点作交直线于点,作的平分线交直线于点,连接.
如图,若点在线段延长线上,点在线段上.
求证:;
如图,连接交于点,交于点,请探索,,之间的数量关系并证明.
请直接写出,和之间的数量关系.
参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.甲
13.
14.
15.南偏西
16.
17.解:原式
.
18.解:在中,,,
,
以点为圆心,长为半径画弧,交于点,
,
.
19.答案不唯一;
证明:四边形是平行四边形,
,,
,
在和中,
,
≌,
.
20.解:与的函数关系式:;
时,
页,
当小明阅读天后,还剩下页书没看.
21.;
该名同学这次竞赛成绩的平均数为;
名,
答:估计竞赛成绩为优秀的人数为名.
22.解:一次函数的图象不经过第四象限,
,
解得;
当时,
,
当时,,当时,,
该一次函数的图象如图所示:
由图象可得,当时,的取值范围是.
23.,;
另一边长为:,
所以,
答:这个矩形的周长为;
当时,
.
24.证明:,
,
四边形是矩形,
,
,
四边形是矩形,
,
,
,
,
四边形为正方形;
解:由知,,四边形为正方形,
,
点为中点,
,
由,的直线解析式为,
由,得直线解析式为,
联立,解得,
,
在中,令得,
,
,
,,
,
的面积为;
平面内存在点,使以点,,为顶点的四边形是菱形,理由如下:
设,,
而,,
当,为对角线时,,的中点重合,且,
,
解得,
;
当,为对角线时,,的中点重合,且,
,
解得或此时不在轴正半轴,舍去,
;
当,为对角线时,,的中点重合,且,
,
解得或舍去,
;
综上所述,的坐标为或或
25.证明:四边形是正方形,
,即,
,
,即,
;
解:,证明如下:
在上取点,使,连接,,如图:
在和中,
,
≌,
,,
四边形是正方形,
,
,
,
,
平分,
,
,,
≌,
,
;
解:当在线段延长线上时,如图:
,,,
≌,
,
,,
≌,
,
;
当在线段上时,如图:
,,,
≌,
,
,,
≌,
,
;
综上所述,当在线段延长线上时,;当在线段上时,.
第1页,共1页
同课章节目录
