2022-2023学年内蒙古包头市青山区七年级(下)期末数学试卷(含答案)
文档属性
| 名称 | 2022-2023学年内蒙古包头市青山区七年级(下)期末数学试卷(含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 431.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-15 16:55:47 | ||
图片预览



文档简介
2022-2023学年内蒙古包头市青山区七年级(下)期末数学试卷
一、选择题:本大题共有8小题,每小题3分,共24分。每小题只有一个正确选项,请将答题卡上对应题目的答案标号涂黑。
1.(3分)围棋起源于中国,古代称之为“弈”,至今已有四千多年的历史,下列图案是轴对称图形的是( )
A. B. C. D.
2.(3分)下列计算正确的是( )
A.b10÷b2=b5 B.m2 m3=m5 C.a5+a5=a10 D.(x3)3=x6
3.(3分)掷一枚质地均匀的硬币5次,下列说法正确的是( )
A.必有5次正面朝上 B.必有2次正面朝上
C.必有3次正面朝上 D.可能有5次正面朝上
4.(3分)世界上最小的开花结果植物是澳大利亚的出水浮萍,这种植物的果实像一个微小的无花果,质量只有0.000000076克,将数0.000000076用科学记数法表示为( )
A.7.6×10﹣8 B.7.6×10﹣9 C.7.6×108 D.7.6×109
5.(3分)如图,点O在直线AB上,OC⊥OD.若∠AOC=120°,则∠BOD的大小为( )
A.30° B.40° C.50° D.60°
6.(3分)某种蔬菜的价格随季节变化如表:
月份x 1 2 3 4 5 6 7 8 9 10 11 12
价格y(元/千克) 5.0 5.5 5.0 4.8 2.0 1.5 1.0 0.9 1.5 3.0 2.5 3.5
根据表中信息,下列结论错误的是( )
A.x是自变量,y是因变量
B.2月份这种蔬菜价格最高,最高为5.5元/千克
C.2~8月份这种蔬菜价格一直在下降
D.8~12月份这种蔬菜价格一直在上升
7.(3分)如图,已知E,B,F,C四点在一条直线上,BC=EF,∠A=∠D,添加以下条件之一,仍不能判定△ABC≌△DEF的是( )
A.∠ABC=∠E B.AC∥DF C.AB∥DE D.AB=DE
8.(3分)如图,在△ABC中,按以下步骤作图:①分别以点B和点C为圆心,以大于的长度为半径作弧,两弧相交于点M和点N;②作直线MN交AB于点D,连接CD.若CD=CA,∠B=25°,则∠ACB的度数为( )
A.105° B.100° C.95° D.90°
二、填空题:本大题共有8小题,每小题3分,共24分。请把答案填在答题卡上对应的横线上。
9.(3分)等腰三角形的顶角为100°,则它的一个底角度数为 .
10.(3分)比较大小:(﹣1)2 50.(填“>”、“<”或“=”)
11.(3分)将一张长方形纸片按如图所示折叠,如果∠1=58°,那么∠2= .
12.(3分)一个不透明的袋子中装有6个球,其中有1个红球、2个绿球和3个黑球,这些球除颜色外都相同,搅匀后任意摸出一个球,摸到绿球的概率是 .
13.(3分)为保护学生的视力,课桌椅的高度均按一定的关系配套设计.已知课桌的高度随着椅子的高度变化而变化,它们之间的关系可以近似地表示为y=1.6x+11,其中y表示课桌的高度(单位:cm),x表示椅子的高度(单位:cm),那么当椅子的高度为40cm时,课桌的高度为 cm.
14.(3分)如图,BD是△ABC的角平分线,若∠C=70°,∠A=40°,则∠ABD= 度.
15.(3分)如图,在△ABC中,AD⊥BC,垂足为D,BE⊥AC,垂足为E,AD与BE相交于点F.AD=BD,若BC=8,DC=3.则AF的长为 .
三、解答题:本大题共有6小题,共52分。请将必要的文字说明、计算过程或推理过程写在答题卡的对应位置。
16.(10分)(1)计算:(2a2)3÷a a3;
(2)计算:[(x﹣2)2+(x+2)(x﹣2)]÷2x.
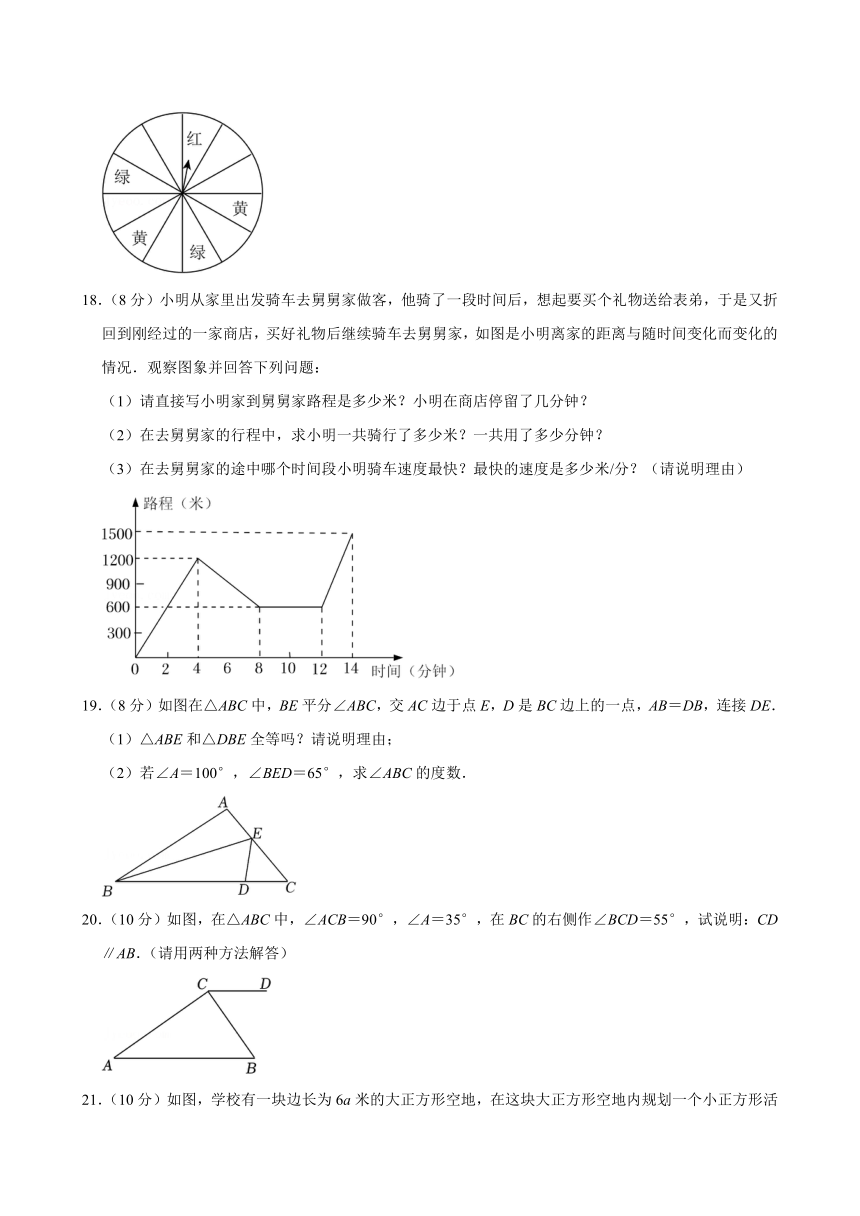
17.(6分)六一儿童节期间,某商场为了吸引顾客,设立了一个可以自由转动的转盘(转盘被等分成12个扇形),并规定:顾客每购买100元的商品,就能获得一次转动转盘的机会.如果转盘停止后,指针正好对准红色、黄色或绿色区域,顾客就可以分别获得相应的奖品(如下表).小明和妈妈购买了125元的商品,可以获得一次转盘的机会,请完成下列问题:
(1)小明获得中性笔的概率是多少?
(2)小明获得奖品的概率是多少?
颜色 奖品
红色 笔袋
黄色 中性笔
绿色 橡皮
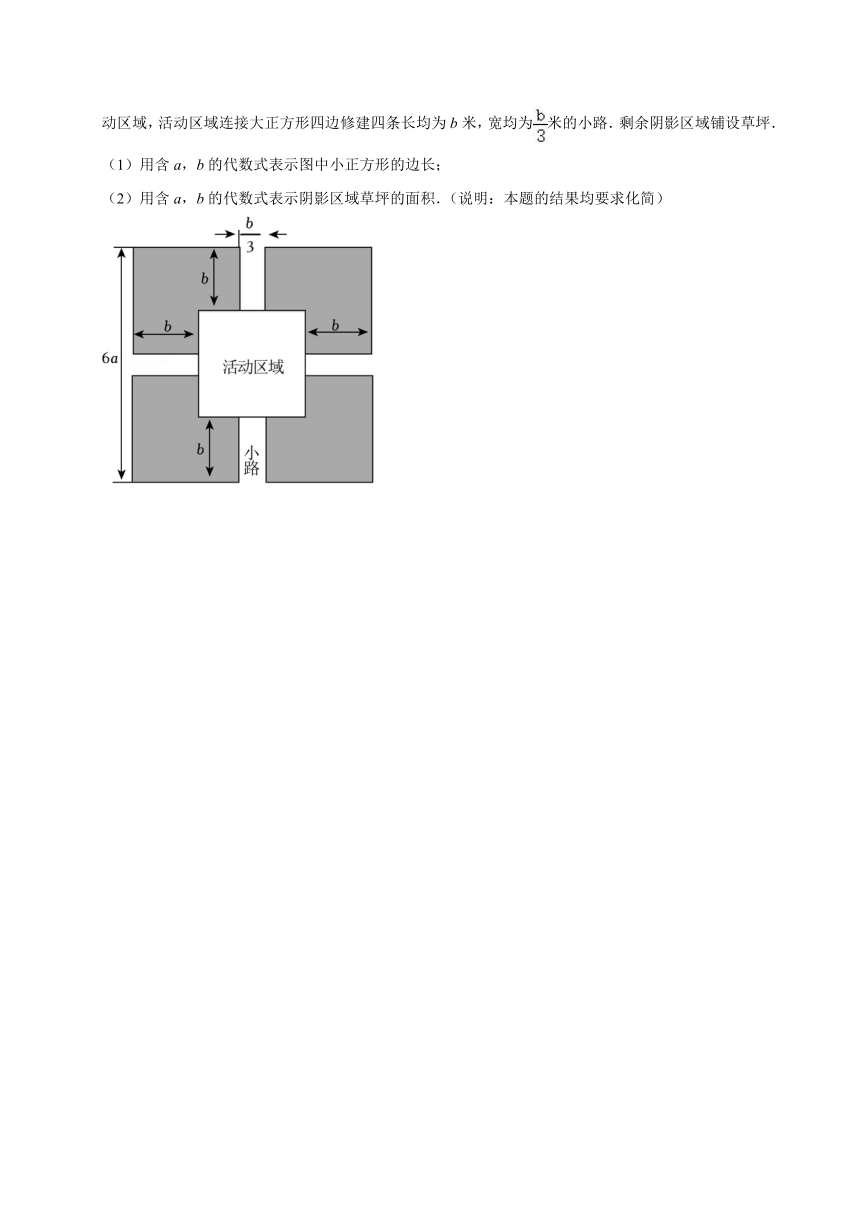
18.(8分)小明从家里出发骑车去舅舅家做客,他骑了一段时间后,想起要买个礼物送给表弟,于是又折回到刚经过的一家商店,买好礼物后继续骑车去舅舅家,如图是小明离家的距离与随时间变化而变化的情况.观察图象并回答下列问题:
(1)请直接写小明家到舅舅家路程是多少米?小明在商店停留了几分钟?
(2)在去舅舅家的行程中,求小明一共骑行了多少米?一共用了多少分钟?
(3)在去舅舅家的途中哪个时间段小明骑车速度最快?最快的速度是多少米/分?(请说明理由)
19.(8分)如图在△ABC中,BE平分∠ABC,交AC边于点E,D是BC边上的一点,AB=DB,连接DE.
(1)△ABE和△DBE全等吗?请说明理由;
(2)若∠A=100°,∠BED=65°,求∠ABC的度数.
20.(10分)如图,在△ABC中,∠ACB=90°,∠A=35°,在BC的右侧作∠BCD=55°,试说明:CD∥AB.(请用两种方法解答)
21.(10分)如图,学校有一块边长为6a米的大正方形空地,在这块大正方形空地内规划一个小正方形活动区域,活动区域连接大正方形四边修建四条长均为b米,宽均为米的小路.剩余阴影区域铺设草坪.
(1)用含a,b的代数式表示图中小正方形的边长;
(2)用含a,b的代数式表示阴影区域草坪的面积.(说明:本题的结果均要求化简)
2022-2023学年内蒙古包头市青山区七年级(下)期末数学试卷
参考答案
一、选择题:本大题共有8小题,每小题3分,共24分。每小题只有一个正确选项,请将答题卡上对应题目的答案标号涂黑。
1.(3分)围棋起源于中国,古代称之为“弈”,至今已有四千多年的历史,下列图案是轴对称图形的是( )
A. B. C. D.
选:C.
2.(3分)下列计算正确的是( )
A.b10÷b2=b5 B.m2 m3=m5 C.a5+a5=a10 D.(x3)3=x6
选:B.
3.(3分)掷一枚质地均匀的硬币5次,下列说法正确的是( )
A.必有5次正面朝上 B.必有2次正面朝上
C.必有3次正面朝上 D.可能有5次正面朝上
选:D.
4.(3分)世界上最小的开花结果植物是澳大利亚的出水浮萍,这种植物的果实像一个微小的无花果,质量只有0.000000076克,将数0.000000076用科学记数法表示为( )
A.7.6×10﹣8 B.7.6×10﹣9 C.7.6×108 D.7.6×109
选:A.
5.(3分)如图,点O在直线AB上,OC⊥OD.若∠AOC=120°,则∠BOD的大小为( )
A.30° B.40° C.50° D.60°
选:A.
6.(3分)某种蔬菜的价格随季节变化如表:
月份x 1 2 3 4 5 6 7 8 9 10 11 12
价格y(元/千克) 5.0 5.5 5.0 4.8 2.0 1.5 1.0 0.9 1.5 3.0 2.5 3.5
根据表中信息,下列结论错误的是( )
A.x是自变量,y是因变量
B.2月份这种蔬菜价格最高,最高为5.5元/千克
C.2~8月份这种蔬菜价格一直在下降
D.8~12月份这种蔬菜价格一直在上升
选:D.
7.(3分)如图,已知E,B,F,C四点在一条直线上,BC=EF,∠A=∠D,添加以下条件之一,仍不能判定△ABC≌△DEF的是( )
A.∠ABC=∠E B.AC∥DF C.AB∥DE D.AB=DE
选:D.
8.(3分)如图,在△ABC中,按以下步骤作图:①分别以点B和点C为圆心,以大于的长度为半径作弧,两弧相交于点M和点N;②作直线MN交AB于点D,连接CD.若CD=CA,∠B=25°,则∠ACB的度数为( )
A.105° B.100° C.95° D.90°
选:A.
二、填空题:本大题共有8小题,每小题3分,共24分。请把答案填在答题卡上对应的横线上。
9.(3分)等腰三角形的顶角为100°,则它的一个底角度数为 40° .
10.(3分)比较大小:(﹣1)2 = 50.(填“>”、“<”或“=”)
11.(3分)将一张长方形纸片按如图所示折叠,如果∠1=58°,那么∠2= 64° .
12.(3分)一个不透明的袋子中装有6个球,其中有1个红球、2个绿球和3个黑球,这些球除颜色外都相同,搅匀后任意摸出一个球,摸到绿球的概率是 .
13.(3分)为保护学生的视力,课桌椅的高度均按一定的关系配套设计.已知课桌的高度随着椅子的高度变化而变化,它们之间的关系可以近似地表示为y=1.6x+11,其中y表示课桌的高度(单位:cm),x表示椅子的高度(单位:cm),那么当椅子的高度为40cm时,课桌的高度为 75 cm.
14.(3分)如图,BD是△ABC的角平分线,若∠C=70°,∠A=40°,则∠ABD= 35 度.
15.(3分)如图,在△ABC中,AD⊥BC,垂足为D,BE⊥AC,垂足为E,AD与BE相交于点F.AD=BD,若BC=8,DC=3.则AF的长为 2 .
三、解答题:本大题共有6小题,共52分。请将必要的文字说明、计算过程或推理过程写在答题卡的对应位置。
16.(10分)(1)计算:(2a2)3÷a a3;
(2)计算:[(x﹣2)2+(x+2)(x﹣2)]÷2x.
【解答】解:(1)(2a2)3÷a a3
=8a6÷a4
=8a2;
(2)[(x﹣2)2+(x+2)(x﹣2)]÷2x
=(x2﹣4x+4+x2﹣4)÷2x
=(2x2﹣4x)÷2x
=x﹣2.
17.(6分)六一儿童节期间,某商场为了吸引顾客,设立了一个可以自由转动的转盘(转盘被等分成12个扇形),并规定:顾客每购买100元的商品,就能获得一次转动转盘的机会.如果转盘停止后,指针正好对准红色、黄色或绿色区域,顾客就可以分别获得相应的奖品(如下表).小明和妈妈购买了125元的商品,可以获得一次转盘的机会,请完成下列问题:
(1)小明获得中性笔的概率是多少?
(2)小明获得奖品的概率是多少?
颜色 奖品
红色 笔袋
黄色 中性笔
绿色 橡皮
【解答】解:(1)∵中性笔对应转盘上黄色区域,转盘停止后,指针正好对准黄色区域,小明就可以获得童话书,而转盘被平均分成12份,而黄色区域有2份,
∴小明获得中性笔的概率是:P==;
(2)∵转盘被平均分成12份,获奖对应的区域有红色区域1份,黄色区域2份,绿色区域2份,
∴小明获得奖品的概率是:P==.
18.(8分)小明从家里出发骑车去舅舅家做客,他骑了一段时间后,想起要买个礼物送给表弟,于是又折回到刚经过的一家商店,买好礼物后继续骑车去舅舅家,如图是小明离家的距离与随时间变化而变化的情况.观察图象并回答下列问题:
(1)请直接写小明家到舅舅家路程是多少米?小明在商店停留了几分钟?
(2)在去舅舅家的行程中,求小明一共骑行了多少米?一共用了多少分钟?
(3)在去舅舅家的途中哪个时间段小明骑车速度最快?最快的速度是多少米/分?(请说明理由)
【解答】解:(1)由所给图象可知,
小明家到舅舅家的路程是1500米,
因为12﹣8=4(分钟),
所以小明在商店停留了4分钟.
(2)因为1200+(1200﹣600)+(1500﹣600)=2700(米),
所以小明一共骑行了2700米.
因为4+(8﹣4)+(14﹣12)=10(分钟),
所以小明一共用了10分钟.
(3)由所给图象可知,
第一段小明的速度为:1200÷4=300(米/分),
第二段小明的速度为:(1200﹣600)÷(8﹣4)=150(米/分),
第三段小明的速度为:(1500﹣600)÷(14﹣12)=450(米/分),
因为450>300>150,
所以小明在12到14分钟骑行的速度最快,最快速度为450米/分.
19.(8分)如图在△ABC中,BE平分∠ABC,交AC边于点E,D是BC边上的一点,AB=DB,连接DE.
(1)△ABE和△DBE全等吗?请说明理由;
(2)若∠A=100°,∠BED=65°,求∠ABC的度数.
【解答】解:(1)△ABE≌△DBE,理由如下:
∵BE平分∠ABC,
∴∠ABE=∠DBE,
在△ABE和△DBE中,
,
∴△ABE≌△DBE(SAS);
(2)由(1)可知,∠ABE=∠DBE,△ABE≌△DBE,
∴∠BEA=∠BED=65°,
∴∠ABE=180°﹣∠A﹣∠BEA=180°﹣100°﹣65°=15°,
∴∠ABC=2∠ABE=30°,
即∠ABC的度数为30°.
20.(10分)如图,在△ABC中,∠ACB=90°,∠A=35°,在BC的右侧作∠BCD=55°,试说明:CD∥AB.(请用两种方法解答)
【解答】证明:方法1,
∵∠ACB=90°,∠A=35°,
∴∠B=90°﹣35°=55°,
∵∠BCD=55°,
∴∠B=∠BCD,
∴CD∥AB.
方法2,
∵∠ACB=90°,∠A=35°,∠BCD=55°,
∴∠A+∠ACB+∠BCD=90°+35°+55°=180°,
∴CD∥AB.
21.(10分)如图,学校有一块边长为6a米的大正方形空地,在这块大正方形空地内规划一个小正方形活动区域,活动区域连接大正方形四边修建四条长均为b米,宽均为米的小路.剩余阴影区域铺设草坪.
(1)用含a,b的代数式表示图中小正方形的边长;
(2)用含a,b的代数式表示阴影区域草坪的面积.(说明:本题的结果均要求化简)
【解答】解:(1)小正方形的边长为(6a﹣2b)米;
(2)阴影区域草坪的面积=大正方形的面积﹣4个长方形的面积﹣中间小正方形的面积
=6a 6a﹣b b×4﹣(6a﹣2b)2
=36a2﹣2b2﹣36a2+24ab﹣4b2
=(﹣6b2+24ab)(平方米).
一、选择题:本大题共有8小题,每小题3分,共24分。每小题只有一个正确选项,请将答题卡上对应题目的答案标号涂黑。
1.(3分)围棋起源于中国,古代称之为“弈”,至今已有四千多年的历史,下列图案是轴对称图形的是( )
A. B. C. D.
2.(3分)下列计算正确的是( )
A.b10÷b2=b5 B.m2 m3=m5 C.a5+a5=a10 D.(x3)3=x6
3.(3分)掷一枚质地均匀的硬币5次,下列说法正确的是( )
A.必有5次正面朝上 B.必有2次正面朝上
C.必有3次正面朝上 D.可能有5次正面朝上
4.(3分)世界上最小的开花结果植物是澳大利亚的出水浮萍,这种植物的果实像一个微小的无花果,质量只有0.000000076克,将数0.000000076用科学记数法表示为( )
A.7.6×10﹣8 B.7.6×10﹣9 C.7.6×108 D.7.6×109
5.(3分)如图,点O在直线AB上,OC⊥OD.若∠AOC=120°,则∠BOD的大小为( )
A.30° B.40° C.50° D.60°
6.(3分)某种蔬菜的价格随季节变化如表:
月份x 1 2 3 4 5 6 7 8 9 10 11 12
价格y(元/千克) 5.0 5.5 5.0 4.8 2.0 1.5 1.0 0.9 1.5 3.0 2.5 3.5
根据表中信息,下列结论错误的是( )
A.x是自变量,y是因变量
B.2月份这种蔬菜价格最高,最高为5.5元/千克
C.2~8月份这种蔬菜价格一直在下降
D.8~12月份这种蔬菜价格一直在上升
7.(3分)如图,已知E,B,F,C四点在一条直线上,BC=EF,∠A=∠D,添加以下条件之一,仍不能判定△ABC≌△DEF的是( )
A.∠ABC=∠E B.AC∥DF C.AB∥DE D.AB=DE
8.(3分)如图,在△ABC中,按以下步骤作图:①分别以点B和点C为圆心,以大于的长度为半径作弧,两弧相交于点M和点N;②作直线MN交AB于点D,连接CD.若CD=CA,∠B=25°,则∠ACB的度数为( )
A.105° B.100° C.95° D.90°
二、填空题:本大题共有8小题,每小题3分,共24分。请把答案填在答题卡上对应的横线上。
9.(3分)等腰三角形的顶角为100°,则它的一个底角度数为 .
10.(3分)比较大小:(﹣1)2 50.(填“>”、“<”或“=”)
11.(3分)将一张长方形纸片按如图所示折叠,如果∠1=58°,那么∠2= .
12.(3分)一个不透明的袋子中装有6个球,其中有1个红球、2个绿球和3个黑球,这些球除颜色外都相同,搅匀后任意摸出一个球,摸到绿球的概率是 .
13.(3分)为保护学生的视力,课桌椅的高度均按一定的关系配套设计.已知课桌的高度随着椅子的高度变化而变化,它们之间的关系可以近似地表示为y=1.6x+11,其中y表示课桌的高度(单位:cm),x表示椅子的高度(单位:cm),那么当椅子的高度为40cm时,课桌的高度为 cm.
14.(3分)如图,BD是△ABC的角平分线,若∠C=70°,∠A=40°,则∠ABD= 度.
15.(3分)如图,在△ABC中,AD⊥BC,垂足为D,BE⊥AC,垂足为E,AD与BE相交于点F.AD=BD,若BC=8,DC=3.则AF的长为 .
三、解答题:本大题共有6小题,共52分。请将必要的文字说明、计算过程或推理过程写在答题卡的对应位置。
16.(10分)(1)计算:(2a2)3÷a a3;
(2)计算:[(x﹣2)2+(x+2)(x﹣2)]÷2x.
17.(6分)六一儿童节期间,某商场为了吸引顾客,设立了一个可以自由转动的转盘(转盘被等分成12个扇形),并规定:顾客每购买100元的商品,就能获得一次转动转盘的机会.如果转盘停止后,指针正好对准红色、黄色或绿色区域,顾客就可以分别获得相应的奖品(如下表).小明和妈妈购买了125元的商品,可以获得一次转盘的机会,请完成下列问题:
(1)小明获得中性笔的概率是多少?
(2)小明获得奖品的概率是多少?
颜色 奖品
红色 笔袋
黄色 中性笔
绿色 橡皮
18.(8分)小明从家里出发骑车去舅舅家做客,他骑了一段时间后,想起要买个礼物送给表弟,于是又折回到刚经过的一家商店,买好礼物后继续骑车去舅舅家,如图是小明离家的距离与随时间变化而变化的情况.观察图象并回答下列问题:
(1)请直接写小明家到舅舅家路程是多少米?小明在商店停留了几分钟?
(2)在去舅舅家的行程中,求小明一共骑行了多少米?一共用了多少分钟?
(3)在去舅舅家的途中哪个时间段小明骑车速度最快?最快的速度是多少米/分?(请说明理由)
19.(8分)如图在△ABC中,BE平分∠ABC,交AC边于点E,D是BC边上的一点,AB=DB,连接DE.
(1)△ABE和△DBE全等吗?请说明理由;
(2)若∠A=100°,∠BED=65°,求∠ABC的度数.
20.(10分)如图,在△ABC中,∠ACB=90°,∠A=35°,在BC的右侧作∠BCD=55°,试说明:CD∥AB.(请用两种方法解答)
21.(10分)如图,学校有一块边长为6a米的大正方形空地,在这块大正方形空地内规划一个小正方形活动区域,活动区域连接大正方形四边修建四条长均为b米,宽均为米的小路.剩余阴影区域铺设草坪.
(1)用含a,b的代数式表示图中小正方形的边长;
(2)用含a,b的代数式表示阴影区域草坪的面积.(说明:本题的结果均要求化简)
2022-2023学年内蒙古包头市青山区七年级(下)期末数学试卷
参考答案
一、选择题:本大题共有8小题,每小题3分,共24分。每小题只有一个正确选项,请将答题卡上对应题目的答案标号涂黑。
1.(3分)围棋起源于中国,古代称之为“弈”,至今已有四千多年的历史,下列图案是轴对称图形的是( )
A. B. C. D.
选:C.
2.(3分)下列计算正确的是( )
A.b10÷b2=b5 B.m2 m3=m5 C.a5+a5=a10 D.(x3)3=x6
选:B.
3.(3分)掷一枚质地均匀的硬币5次,下列说法正确的是( )
A.必有5次正面朝上 B.必有2次正面朝上
C.必有3次正面朝上 D.可能有5次正面朝上
选:D.
4.(3分)世界上最小的开花结果植物是澳大利亚的出水浮萍,这种植物的果实像一个微小的无花果,质量只有0.000000076克,将数0.000000076用科学记数法表示为( )
A.7.6×10﹣8 B.7.6×10﹣9 C.7.6×108 D.7.6×109
选:A.
5.(3分)如图,点O在直线AB上,OC⊥OD.若∠AOC=120°,则∠BOD的大小为( )
A.30° B.40° C.50° D.60°
选:A.
6.(3分)某种蔬菜的价格随季节变化如表:
月份x 1 2 3 4 5 6 7 8 9 10 11 12
价格y(元/千克) 5.0 5.5 5.0 4.8 2.0 1.5 1.0 0.9 1.5 3.0 2.5 3.5
根据表中信息,下列结论错误的是( )
A.x是自变量,y是因变量
B.2月份这种蔬菜价格最高,最高为5.5元/千克
C.2~8月份这种蔬菜价格一直在下降
D.8~12月份这种蔬菜价格一直在上升
选:D.
7.(3分)如图,已知E,B,F,C四点在一条直线上,BC=EF,∠A=∠D,添加以下条件之一,仍不能判定△ABC≌△DEF的是( )
A.∠ABC=∠E B.AC∥DF C.AB∥DE D.AB=DE
选:D.
8.(3分)如图,在△ABC中,按以下步骤作图:①分别以点B和点C为圆心,以大于的长度为半径作弧,两弧相交于点M和点N;②作直线MN交AB于点D,连接CD.若CD=CA,∠B=25°,则∠ACB的度数为( )
A.105° B.100° C.95° D.90°
选:A.
二、填空题:本大题共有8小题,每小题3分,共24分。请把答案填在答题卡上对应的横线上。
9.(3分)等腰三角形的顶角为100°,则它的一个底角度数为 40° .
10.(3分)比较大小:(﹣1)2 = 50.(填“>”、“<”或“=”)
11.(3分)将一张长方形纸片按如图所示折叠,如果∠1=58°,那么∠2= 64° .
12.(3分)一个不透明的袋子中装有6个球,其中有1个红球、2个绿球和3个黑球,这些球除颜色外都相同,搅匀后任意摸出一个球,摸到绿球的概率是 .
13.(3分)为保护学生的视力,课桌椅的高度均按一定的关系配套设计.已知课桌的高度随着椅子的高度变化而变化,它们之间的关系可以近似地表示为y=1.6x+11,其中y表示课桌的高度(单位:cm),x表示椅子的高度(单位:cm),那么当椅子的高度为40cm时,课桌的高度为 75 cm.
14.(3分)如图,BD是△ABC的角平分线,若∠C=70°,∠A=40°,则∠ABD= 35 度.
15.(3分)如图,在△ABC中,AD⊥BC,垂足为D,BE⊥AC,垂足为E,AD与BE相交于点F.AD=BD,若BC=8,DC=3.则AF的长为 2 .
三、解答题:本大题共有6小题,共52分。请将必要的文字说明、计算过程或推理过程写在答题卡的对应位置。
16.(10分)(1)计算:(2a2)3÷a a3;
(2)计算:[(x﹣2)2+(x+2)(x﹣2)]÷2x.
【解答】解:(1)(2a2)3÷a a3
=8a6÷a4
=8a2;
(2)[(x﹣2)2+(x+2)(x﹣2)]÷2x
=(x2﹣4x+4+x2﹣4)÷2x
=(2x2﹣4x)÷2x
=x﹣2.
17.(6分)六一儿童节期间,某商场为了吸引顾客,设立了一个可以自由转动的转盘(转盘被等分成12个扇形),并规定:顾客每购买100元的商品,就能获得一次转动转盘的机会.如果转盘停止后,指针正好对准红色、黄色或绿色区域,顾客就可以分别获得相应的奖品(如下表).小明和妈妈购买了125元的商品,可以获得一次转盘的机会,请完成下列问题:
(1)小明获得中性笔的概率是多少?
(2)小明获得奖品的概率是多少?
颜色 奖品
红色 笔袋
黄色 中性笔
绿色 橡皮
【解答】解:(1)∵中性笔对应转盘上黄色区域,转盘停止后,指针正好对准黄色区域,小明就可以获得童话书,而转盘被平均分成12份,而黄色区域有2份,
∴小明获得中性笔的概率是:P==;
(2)∵转盘被平均分成12份,获奖对应的区域有红色区域1份,黄色区域2份,绿色区域2份,
∴小明获得奖品的概率是:P==.
18.(8分)小明从家里出发骑车去舅舅家做客,他骑了一段时间后,想起要买个礼物送给表弟,于是又折回到刚经过的一家商店,买好礼物后继续骑车去舅舅家,如图是小明离家的距离与随时间变化而变化的情况.观察图象并回答下列问题:
(1)请直接写小明家到舅舅家路程是多少米?小明在商店停留了几分钟?
(2)在去舅舅家的行程中,求小明一共骑行了多少米?一共用了多少分钟?
(3)在去舅舅家的途中哪个时间段小明骑车速度最快?最快的速度是多少米/分?(请说明理由)
【解答】解:(1)由所给图象可知,
小明家到舅舅家的路程是1500米,
因为12﹣8=4(分钟),
所以小明在商店停留了4分钟.
(2)因为1200+(1200﹣600)+(1500﹣600)=2700(米),
所以小明一共骑行了2700米.
因为4+(8﹣4)+(14﹣12)=10(分钟),
所以小明一共用了10分钟.
(3)由所给图象可知,
第一段小明的速度为:1200÷4=300(米/分),
第二段小明的速度为:(1200﹣600)÷(8﹣4)=150(米/分),
第三段小明的速度为:(1500﹣600)÷(14﹣12)=450(米/分),
因为450>300>150,
所以小明在12到14分钟骑行的速度最快,最快速度为450米/分.
19.(8分)如图在△ABC中,BE平分∠ABC,交AC边于点E,D是BC边上的一点,AB=DB,连接DE.
(1)△ABE和△DBE全等吗?请说明理由;
(2)若∠A=100°,∠BED=65°,求∠ABC的度数.
【解答】解:(1)△ABE≌△DBE,理由如下:
∵BE平分∠ABC,
∴∠ABE=∠DBE,
在△ABE和△DBE中,
,
∴△ABE≌△DBE(SAS);
(2)由(1)可知,∠ABE=∠DBE,△ABE≌△DBE,
∴∠BEA=∠BED=65°,
∴∠ABE=180°﹣∠A﹣∠BEA=180°﹣100°﹣65°=15°,
∴∠ABC=2∠ABE=30°,
即∠ABC的度数为30°.
20.(10分)如图,在△ABC中,∠ACB=90°,∠A=35°,在BC的右侧作∠BCD=55°,试说明:CD∥AB.(请用两种方法解答)
【解答】证明:方法1,
∵∠ACB=90°,∠A=35°,
∴∠B=90°﹣35°=55°,
∵∠BCD=55°,
∴∠B=∠BCD,
∴CD∥AB.
方法2,
∵∠ACB=90°,∠A=35°,∠BCD=55°,
∴∠A+∠ACB+∠BCD=90°+35°+55°=180°,
∴CD∥AB.
21.(10分)如图,学校有一块边长为6a米的大正方形空地,在这块大正方形空地内规划一个小正方形活动区域,活动区域连接大正方形四边修建四条长均为b米,宽均为米的小路.剩余阴影区域铺设草坪.
(1)用含a,b的代数式表示图中小正方形的边长;
(2)用含a,b的代数式表示阴影区域草坪的面积.(说明:本题的结果均要求化简)
【解答】解:(1)小正方形的边长为(6a﹣2b)米;
(2)阴影区域草坪的面积=大正方形的面积﹣4个长方形的面积﹣中间小正方形的面积
=6a 6a﹣b b×4﹣(6a﹣2b)2
=36a2﹣2b2﹣36a2+24ab﹣4b2
=(﹣6b2+24ab)(平方米).
同课章节目录
