第26章 反比例函数—九年级下册数学人教版(2012)单元质检卷(A卷)(含答案)
文档属性
| 名称 | 第26章 反比例函数—九年级下册数学人教版(2012)单元质检卷(A卷)(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-16 00:00:00 | ||
图片预览



文档简介
(1)反比例函数—九年级下册数学人教版(2012)单元质检卷(A卷)
【满分:120】
一、选择题:(本大题共10小题,每小题4分,共40分,给出的四个选项中,只有一项是符合题目要求的)
1.若双曲线经过点,则的值是( )
A. B.3 C. D.
2.已知点在反比例函数的图象上,则m的值是( )
A. B. C.6 D.24
3.反比例函数的图象一定经过的点是( )
A. B. C. D.
4.若反比例函数的图象在第二、四象限,则a的值可以为( )
A.2 B.3 C.4 D.5
5.如图,函数和的图象在同一平面直角坐标系中,则该坐标系的原点是( )
A.点M B.点N C.点P D.点Q
6.在平面直角坐标系中,函数的图像与坐标轴的交点个数是( )
A.0 B.1 C.2 D.4
7.点,,,在反比例函数图象上,则,,,中最小的是( )
A. B. C. D.
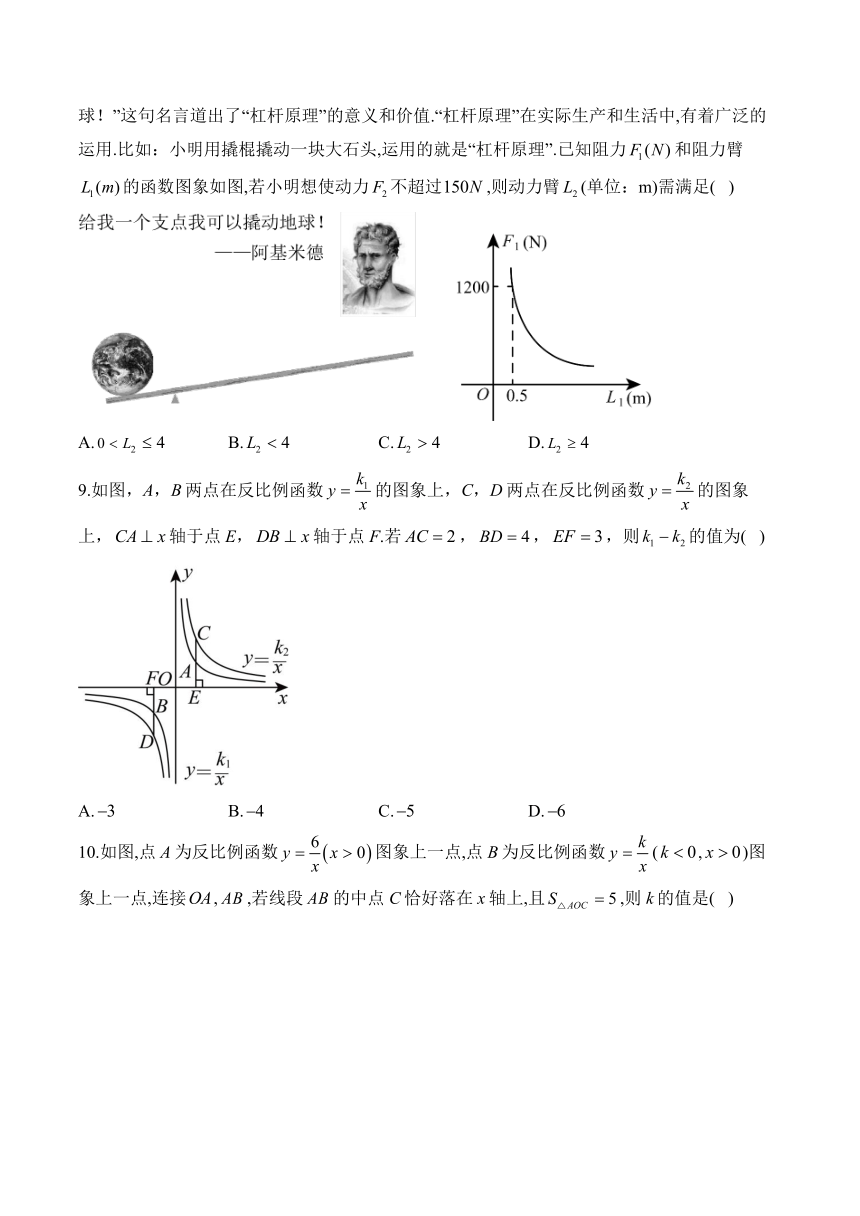
8.伟大的古希腊哲学家、数学家、物理学家阿基米德有句名言:“给我一个支点,我可以撬动地球!”这句名言道出了“杠杆原理”的意义和价值.“杠杆原理”在实际生产和生活中,有着广泛的运用.比如:小明用撬棍撬动一块大石头,运用的就是“杠杆原理”.已知阻力和阻力臂的函数图象如图,若小明想使动力不超过,则动力臂(单位:m)需满足( )
A. B. C. D.
9.如图,A,B两点在反比例函数的图象上,C,D两点在反比例函数的图象上,轴于点E,轴于点F.若,,,则的值为( )
A. B. C. D.
10.如图,点A为反比例函数图象上一点,点B为反比例函数(,)图象上一点,连接,,若线段的中点C恰好落在x轴上,且,则k的值是( )
A. B. C. D.
二、填空题(每小题4分,共20分)
11.已知,和是同一个反比例函数图象上的两个点,则________.
12.如图,反比例函数经过点A、点B,则______.
13.在温度不变的条件下,通过一次又一次地对汽缸顶部的活塞加压,加压后气体对汽缸壁所产生的压强P()与汽缸内气体的体积V()成反比例,P关于V的函数图象如图所示.若压强由加压到,则气体体积压缩了___________.
14.若点,都在反比例函数(k是常数)的图象上,且,则m的范围是_______________.
15.如图,的顶点A在反比例函数的图象上,顶点B在x轴的负半轴上,点E为边的中点,若反比例函数的图象经过点C,E,则m与n的关系为____________.
三、解答题(本大题共6小题,共计60分,解答题应写出演算步骤或证明过程)
16.(8分)已知y是x的反比例函数,且函数图象过点.
(1)求y与x的函数关系式;
(2)当x取何值时,.
17.(8分)某中学组织学生到商场参加社会实践活动,他们参与了某种品牌运动鞋的销售工作.已知该品牌运动鞋每双的进价为120元,为寻求合适的销售价格进行了4天的试销,试销情况如表所示:
第1天 第2天 第3天 第4天
售价x(元/双) 150 200 250 300
销售量y(双) 40 30 24 20
(1)观察表中数据,x,y满足什么关系式?并写出用x表示y的函数表达式;
(2)若商场计划每天的销售利润为2000元,则每双运动鞋的售价应定为多少元?
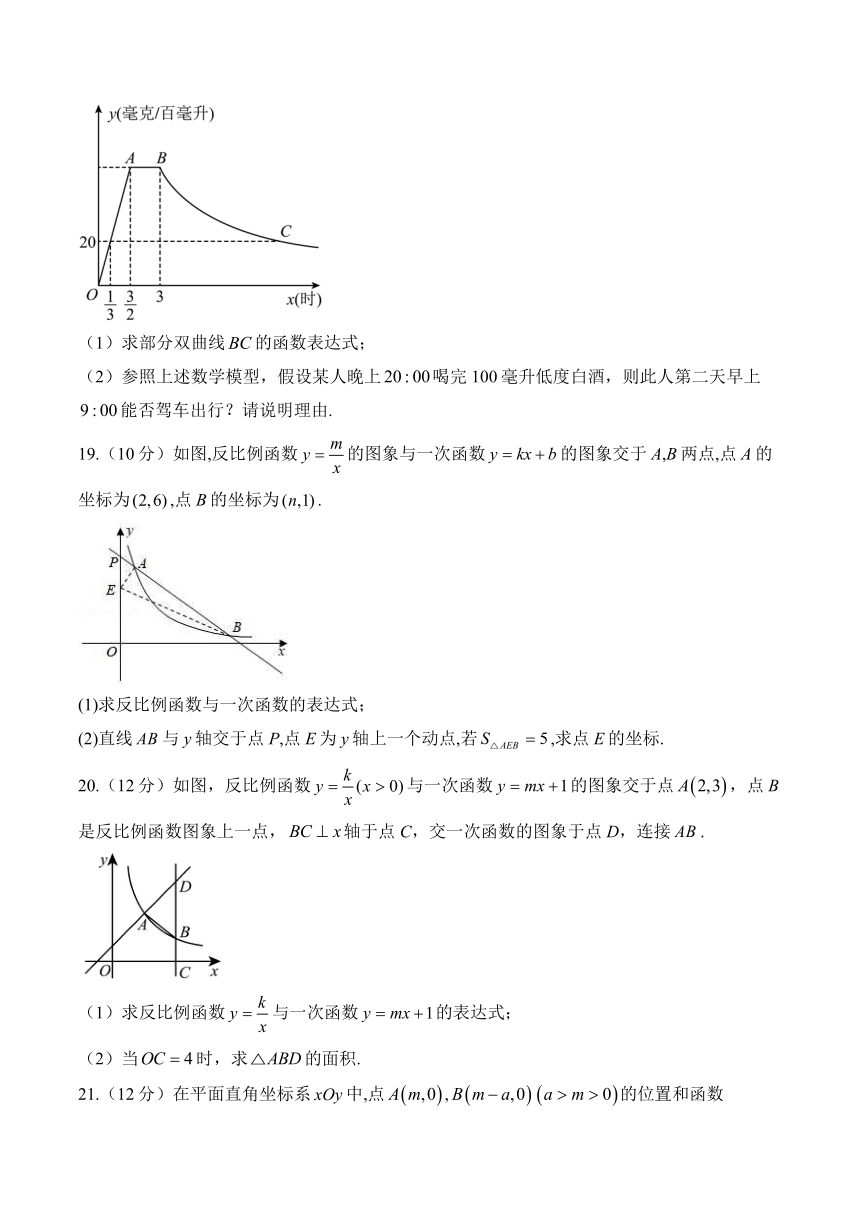
18.(10分)某生物小组探究“酒精对人体的影响”,资料显示,一般饮用低度白酒100毫升后,血液中酒精含量y(毫克/百毫升)与时间x(时)的关系可近似的用如图所示的图象表示.国家规定,人体血液中的酒精含量大于或等于20(毫克/百毫升)时属于“酒后驾驶”,不能驾车上路.
(1)求部分双曲线的函数表达式;
(2)参照上述数学模型,假设某人晚上喝完100毫升低度白酒,则此人第二天早上能否驾车出行?请说明理由.
19.(10分)如图,反比例函数的图象与一次函数的图象交于A,B两点,点A的坐标为,点B的坐标为.
(1)求反比例函数与一次函数的表达式;
(2)直线与y轴交于点P,点E为y轴上一个动点,若,求点E的坐标.
20.(12分)如图,反比例函数与一次函数的图象交于点,点B是反比例函数图象上一点,轴于点C,交一次函数的图象于点D,连接.
(1)求反比例函数与一次函数的表达式;
(2)当时,求的面积.
21.(12分)在平面直角坐标系中,点,的位置和函数、的图象如图所示.以为边在x轴上方作正方形,边与函数的图象相交于点E,边与函数、的图象分别相交于点G、H,一次函数的图象经过点E、G,与y轴相交于点P,连接.
(1)若,,
①求函数的表达式及的面积;
②直接写出使成立的x的范围;
(2)当a、m在满足的条件下任意变化时,的面积是否变化?请说明理由;
答案以及解析
1.答案:B
解析:把代入得:,
解得:,
故选:B.
2.答案:A
解析:把点代入,得:.
故选:A
3.答案:C
解析:反比例函数中,,
A、,此点不在反比例函数的图象上,故本选项不符合题意;
B、,此点不在反比例函数的图象上,故本选项不符合题意;
C、,此点在反比例函数的图象上,故本选项符合题意;
D、,此点不在反比例函数的图象上,故本选项不符合题意;
故选:C.
4.答案:A
解析:∵反比例函数的图象在第二、四象限,
∴,
解得,,
故选:A.
5.答案:B
解析:在函数和中,
∵,,
∴函数的图象在第一象限,函数的图象在第四象限,
∴该坐标系的原点是点N,
故选:B.
6.答案:B
解析:当时,,与y轴的交点为;
由于是分式,且当时,,即,
与x轴没有交点.
函数的图像与坐标轴的交点个数是1个,
故选:B.
7.答案:D
解析:由反比例函数解析式可知:,
∴在每个象限内,y随x的增大而减小,
∵点,,,在反比例函数图象上,
∴,
故选D.
8.答案:D
解析:阻力和阻力臂的函数关系式为,
点在该函数图象上,
,
解得,
阻力和阻力臂的函数关系式为,
,
,
当时,,
小明想使动力不超过,则动力臂(单位:m)需满足,
故选:D.
9.答案:B
解析:设点,,,,则,
,
解得.
同理,可得,
解得.
,
,
解得,
故选:B.
10.答案:D
解析:过点A作轴,垂足为E,过点B作轴,垂足为F,连接,
∴
∵C是线段的中点,
∴,
∵,
∴,
∴,,
∵,
∴,
∵点A为反比例函数图象上一点,
∴,
∴,
∴,
∵点B为反比例函数(,)图象上一点,
∴,
故选:D.
11.答案:-6
解析:,和是同一个反比例函数图象上的两个点,
,
.
故答案为-6.
12.答案:2
解析:由图可知,,
将代入,
得:,
,
将代入得:,
解得:,
故答案为:2.
13.答案:20
解析:设P关于V的函数解析式为,由图象可把点代入得:,
∴P关于V的函数解析式为,
∴当时,则,
当时,则,
∴压强由加压到,则气体体积压缩了;
故答案为20.
14.答案:
解析:由反比例函数(k是常数)可知图象位于一、三象限,每一象限内y随x的增大而减小.
点,都在反比例函数(k是常数)的图象上,且,
点,不在同一象限,
点第一象限,点在第三象限.
,
.
故答案为:.
15.答案:
解析:∵中,,
∴点A和点C纵坐标相同,
∵点A在反比例函数上,点C在反比例函数上,
设,则,
∴,
∴,
∵点E为边的中点,
∴点E坐标为,
即,
∵点E在反比例函数上,
∴,
化简得,
故答案为:.
16.答案:(1)
(2)
解析:(1)设该反比例函数的表达式为:;
将代入得,,解得:
∴.
(2)将代入中,
,解得:.
17.答案:(1),
(2)若商场计划每天的销售利润为2000元,则每双运动鞋的售价应定为180元
解析:(1)由表中数据得:,
,
是x的反比例函数,
故所求函数关系式为.
(2)由题意得:,
把代入得:,
解得:.
经检验,是原方程的根,符合题意.
答:若商场计划每天的销售利润为2000元,则每双运动鞋的售价应定为180元.
18.答案:(1)
(2)不能,理由见解析
解析:(1)依题意,设的解析式为,将点代入得:,
解得:,
,
当时,,即,
,
设双曲线的解析式为,将点代入得:,
;
(2)不能,理由如下
在中,当时,,
从晚上到第二天早上时间间距为13小时,
,
第二天早上不能驾车出行.
19.答案:(1)
(2)或
解析:(1)把点代入,得,
反比例函数的表达式为,点代入,得,
点B的坐标为,
直线过点,,,解得,
一次函数的表达式为;
(2)设点E的坐标为,连接,,则点,
,
,,
,解得,,
点E的坐标为或.
20.答案:(1),
(2)
解析:(1)反比例函数与一次函数的图象交于点,
,,
,,
反比例函数为:,一次函数的解析式为:.
(2),
,
轴于点C,交一次函数的图象于点D,
点B的横坐标为4.点D的横坐标为4.
,,
,,
,
过点B作轴交一次函数的图象交于点E,过点A作与点F,
,点E的纵坐标为,
,
把代入,得,
,
点,
,
.
21.答案:(1)①,
②,
(2)当a、m在满足的条件下任意变化时,的面积不变化,理由见解析
解析:(1)①,,
点,,,,
∴
点,,,
一次函数的图象经过点E、G,
设,则
,,
函数的表达式为,
,
,
;
②当时,则,即,
当或时,;
(2)的面积不变化.理由如下:
点,,,,
点,,,
设,则,
,,
,
.
当a、m在满足的条件下任意变化时,的面积不变化.
【满分:120】
一、选择题:(本大题共10小题,每小题4分,共40分,给出的四个选项中,只有一项是符合题目要求的)
1.若双曲线经过点,则的值是( )
A. B.3 C. D.
2.已知点在反比例函数的图象上,则m的值是( )
A. B. C.6 D.24
3.反比例函数的图象一定经过的点是( )
A. B. C. D.
4.若反比例函数的图象在第二、四象限,则a的值可以为( )
A.2 B.3 C.4 D.5
5.如图,函数和的图象在同一平面直角坐标系中,则该坐标系的原点是( )
A.点M B.点N C.点P D.点Q
6.在平面直角坐标系中,函数的图像与坐标轴的交点个数是( )
A.0 B.1 C.2 D.4
7.点,,,在反比例函数图象上,则,,,中最小的是( )
A. B. C. D.
8.伟大的古希腊哲学家、数学家、物理学家阿基米德有句名言:“给我一个支点,我可以撬动地球!”这句名言道出了“杠杆原理”的意义和价值.“杠杆原理”在实际生产和生活中,有着广泛的运用.比如:小明用撬棍撬动一块大石头,运用的就是“杠杆原理”.已知阻力和阻力臂的函数图象如图,若小明想使动力不超过,则动力臂(单位:m)需满足( )
A. B. C. D.
9.如图,A,B两点在反比例函数的图象上,C,D两点在反比例函数的图象上,轴于点E,轴于点F.若,,,则的值为( )
A. B. C. D.
10.如图,点A为反比例函数图象上一点,点B为反比例函数(,)图象上一点,连接,,若线段的中点C恰好落在x轴上,且,则k的值是( )
A. B. C. D.
二、填空题(每小题4分,共20分)
11.已知,和是同一个反比例函数图象上的两个点,则________.
12.如图,反比例函数经过点A、点B,则______.
13.在温度不变的条件下,通过一次又一次地对汽缸顶部的活塞加压,加压后气体对汽缸壁所产生的压强P()与汽缸内气体的体积V()成反比例,P关于V的函数图象如图所示.若压强由加压到,则气体体积压缩了___________.
14.若点,都在反比例函数(k是常数)的图象上,且,则m的范围是_______________.
15.如图,的顶点A在反比例函数的图象上,顶点B在x轴的负半轴上,点E为边的中点,若反比例函数的图象经过点C,E,则m与n的关系为____________.
三、解答题(本大题共6小题,共计60分,解答题应写出演算步骤或证明过程)
16.(8分)已知y是x的反比例函数,且函数图象过点.
(1)求y与x的函数关系式;
(2)当x取何值时,.
17.(8分)某中学组织学生到商场参加社会实践活动,他们参与了某种品牌运动鞋的销售工作.已知该品牌运动鞋每双的进价为120元,为寻求合适的销售价格进行了4天的试销,试销情况如表所示:
第1天 第2天 第3天 第4天
售价x(元/双) 150 200 250 300
销售量y(双) 40 30 24 20
(1)观察表中数据,x,y满足什么关系式?并写出用x表示y的函数表达式;
(2)若商场计划每天的销售利润为2000元,则每双运动鞋的售价应定为多少元?
18.(10分)某生物小组探究“酒精对人体的影响”,资料显示,一般饮用低度白酒100毫升后,血液中酒精含量y(毫克/百毫升)与时间x(时)的关系可近似的用如图所示的图象表示.国家规定,人体血液中的酒精含量大于或等于20(毫克/百毫升)时属于“酒后驾驶”,不能驾车上路.
(1)求部分双曲线的函数表达式;
(2)参照上述数学模型,假设某人晚上喝完100毫升低度白酒,则此人第二天早上能否驾车出行?请说明理由.
19.(10分)如图,反比例函数的图象与一次函数的图象交于A,B两点,点A的坐标为,点B的坐标为.
(1)求反比例函数与一次函数的表达式;
(2)直线与y轴交于点P,点E为y轴上一个动点,若,求点E的坐标.
20.(12分)如图,反比例函数与一次函数的图象交于点,点B是反比例函数图象上一点,轴于点C,交一次函数的图象于点D,连接.
(1)求反比例函数与一次函数的表达式;
(2)当时,求的面积.
21.(12分)在平面直角坐标系中,点,的位置和函数、的图象如图所示.以为边在x轴上方作正方形,边与函数的图象相交于点E,边与函数、的图象分别相交于点G、H,一次函数的图象经过点E、G,与y轴相交于点P,连接.
(1)若,,
①求函数的表达式及的面积;
②直接写出使成立的x的范围;
(2)当a、m在满足的条件下任意变化时,的面积是否变化?请说明理由;
答案以及解析
1.答案:B
解析:把代入得:,
解得:,
故选:B.
2.答案:A
解析:把点代入,得:.
故选:A
3.答案:C
解析:反比例函数中,,
A、,此点不在反比例函数的图象上,故本选项不符合题意;
B、,此点不在反比例函数的图象上,故本选项不符合题意;
C、,此点在反比例函数的图象上,故本选项符合题意;
D、,此点不在反比例函数的图象上,故本选项不符合题意;
故选:C.
4.答案:A
解析:∵反比例函数的图象在第二、四象限,
∴,
解得,,
故选:A.
5.答案:B
解析:在函数和中,
∵,,
∴函数的图象在第一象限,函数的图象在第四象限,
∴该坐标系的原点是点N,
故选:B.
6.答案:B
解析:当时,,与y轴的交点为;
由于是分式,且当时,,即,
与x轴没有交点.
函数的图像与坐标轴的交点个数是1个,
故选:B.
7.答案:D
解析:由反比例函数解析式可知:,
∴在每个象限内,y随x的增大而减小,
∵点,,,在反比例函数图象上,
∴,
故选D.
8.答案:D
解析:阻力和阻力臂的函数关系式为,
点在该函数图象上,
,
解得,
阻力和阻力臂的函数关系式为,
,
,
当时,,
小明想使动力不超过,则动力臂(单位:m)需满足,
故选:D.
9.答案:B
解析:设点,,,,则,
,
解得.
同理,可得,
解得.
,
,
解得,
故选:B.
10.答案:D
解析:过点A作轴,垂足为E,过点B作轴,垂足为F,连接,
∴
∵C是线段的中点,
∴,
∵,
∴,
∴,,
∵,
∴,
∵点A为反比例函数图象上一点,
∴,
∴,
∴,
∵点B为反比例函数(,)图象上一点,
∴,
故选:D.
11.答案:-6
解析:,和是同一个反比例函数图象上的两个点,
,
.
故答案为-6.
12.答案:2
解析:由图可知,,
将代入,
得:,
,
将代入得:,
解得:,
故答案为:2.
13.答案:20
解析:设P关于V的函数解析式为,由图象可把点代入得:,
∴P关于V的函数解析式为,
∴当时,则,
当时,则,
∴压强由加压到,则气体体积压缩了;
故答案为20.
14.答案:
解析:由反比例函数(k是常数)可知图象位于一、三象限,每一象限内y随x的增大而减小.
点,都在反比例函数(k是常数)的图象上,且,
点,不在同一象限,
点第一象限,点在第三象限.
,
.
故答案为:.
15.答案:
解析:∵中,,
∴点A和点C纵坐标相同,
∵点A在反比例函数上,点C在反比例函数上,
设,则,
∴,
∴,
∵点E为边的中点,
∴点E坐标为,
即,
∵点E在反比例函数上,
∴,
化简得,
故答案为:.
16.答案:(1)
(2)
解析:(1)设该反比例函数的表达式为:;
将代入得,,解得:
∴.
(2)将代入中,
,解得:.
17.答案:(1),
(2)若商场计划每天的销售利润为2000元,则每双运动鞋的售价应定为180元
解析:(1)由表中数据得:,
,
是x的反比例函数,
故所求函数关系式为.
(2)由题意得:,
把代入得:,
解得:.
经检验,是原方程的根,符合题意.
答:若商场计划每天的销售利润为2000元,则每双运动鞋的售价应定为180元.
18.答案:(1)
(2)不能,理由见解析
解析:(1)依题意,设的解析式为,将点代入得:,
解得:,
,
当时,,即,
,
设双曲线的解析式为,将点代入得:,
;
(2)不能,理由如下
在中,当时,,
从晚上到第二天早上时间间距为13小时,
,
第二天早上不能驾车出行.
19.答案:(1)
(2)或
解析:(1)把点代入,得,
反比例函数的表达式为,点代入,得,
点B的坐标为,
直线过点,,,解得,
一次函数的表达式为;
(2)设点E的坐标为,连接,,则点,
,
,,
,解得,,
点E的坐标为或.
20.答案:(1),
(2)
解析:(1)反比例函数与一次函数的图象交于点,
,,
,,
反比例函数为:,一次函数的解析式为:.
(2),
,
轴于点C,交一次函数的图象于点D,
点B的横坐标为4.点D的横坐标为4.
,,
,,
,
过点B作轴交一次函数的图象交于点E,过点A作与点F,
,点E的纵坐标为,
,
把代入,得,
,
点,
,
.
21.答案:(1)①,
②,
(2)当a、m在满足的条件下任意变化时,的面积不变化,理由见解析
解析:(1)①,,
点,,,,
∴
点,,,
一次函数的图象经过点E、G,
设,则
,,
函数的表达式为,
,
,
;
②当时,则,即,
当或时,;
(2)的面积不变化.理由如下:
点,,,,
点,,,
设,则,
,,
,
.
当a、m在满足的条件下任意变化时,的面积不变化.
