第26章 反比例函数—九年级下册数学人教版(2012)单元质检卷(B卷)(含答案)
文档属性
| 名称 | 第26章 反比例函数—九年级下册数学人教版(2012)单元质检卷(B卷)(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1010.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-16 14:42:21 | ||
图片预览



文档简介
(2)反比例函数—九年级下册数学人教版(2012)单元质检卷(B卷)
【满分:120】
一、选择题:(本大题共10小题,每小题4分,共40分,给出的四个选项中,只有一项是符合题目要求的)
1.函数中,自变量的取值范围是( )
A. B. C. D.全体实数
2.若反比例函数的图象经过点,则该函数图象一定经过( )
A. B. C. D.
3.如果点在反比例函数的图象上,则代数式的值为( )
A.0 B. C.2 D.
4.对于反比例函数,在每个象限内y都随x的增大而增大,则下列点可能在这个函数图象上的为( )
A. B. C. D.
5.反比例函数与一次函数在同一平面直角坐标系中的图象大致是( )
A. B. C. D.
6.如图是反比例函数的图象,点是反比例函数图象上任意一点,过点A作轴于点B,连接,则的面积是( )
A.2 B.1 C. D.
7.已知反比例函数,则下列描述正确的是( )
A.图象必经过
B.图象位于一、三象限
C.y随x的增大而增大
D.如果点在它的图象上,则点也在它的图象上
8.密闭容器内有一定质量的二氧化碳,当容器的体积V(单位:)变化时,气体的密度(单位:随之变化.已知密度与体积V是反比例函数关系,它的图象如图所示,当时,.根据图象可知,下列说法不正确的是( )
A.与V的函数关系式是
B.当时,
C.当时,
D.当时,的变化范围是
9.已知点,在反比例函数(k为常数)图像上,.若,则的值为( ).
A.0 B.负数 C.正数 D.非负数
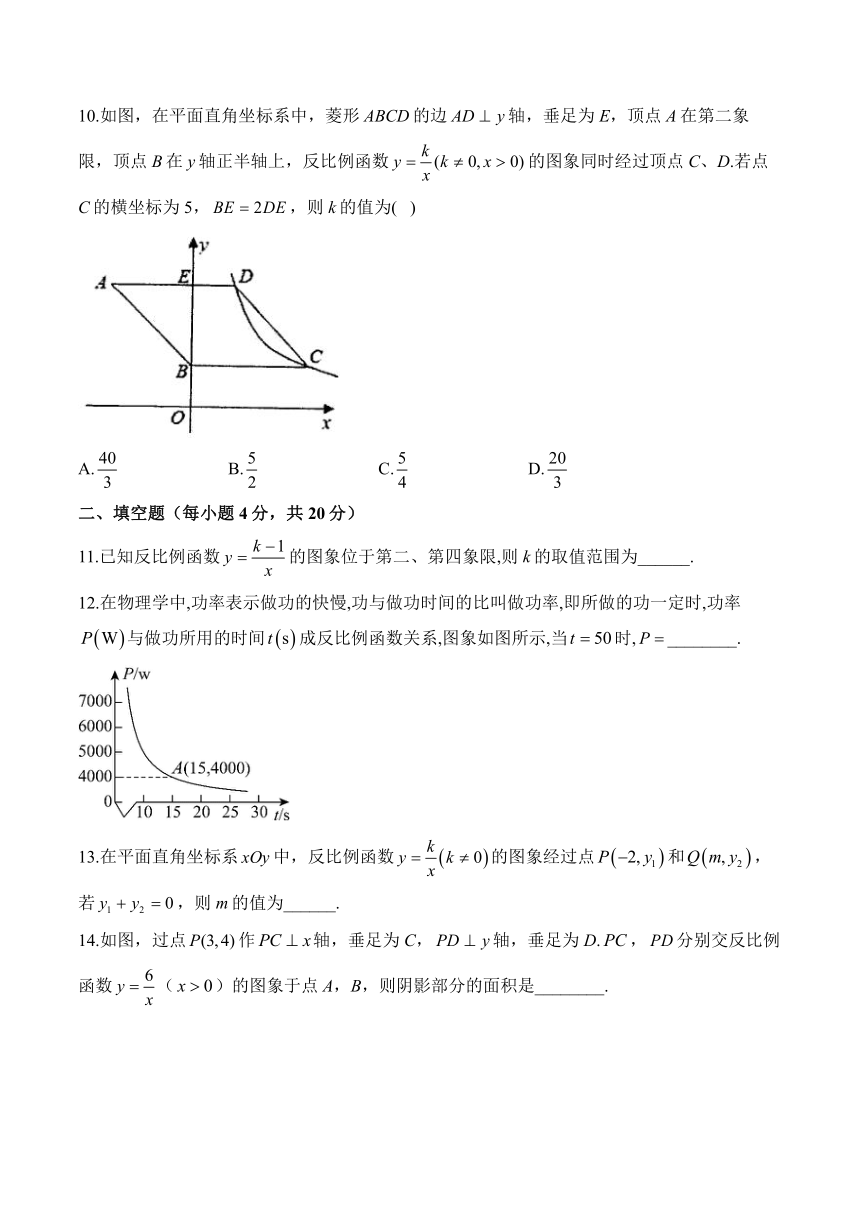
10.如图,在平面直角坐标系中,菱形ABCD的边轴,垂足为E,顶点A在第二象限,顶点B在y轴正半轴上,反比例函数的图象同时经过顶点C、D.若点C的横坐标为5,,则k的值为( )
A. B. C. D.
二、填空题(每小题4分,共20分)
11.已知反比例函数的图象位于第二、第四象限,则k的取值范围为______.
12.在物理学中,功率表示做功的快慢,功与做功时间的比叫做功率,即所做的功一定时,功率与做功所用的时间成反比例函数关系,图象如图所示,当时,________.
13.在平面直角坐标系中,反比例函数的图象经过点和,若,则m的值为______.
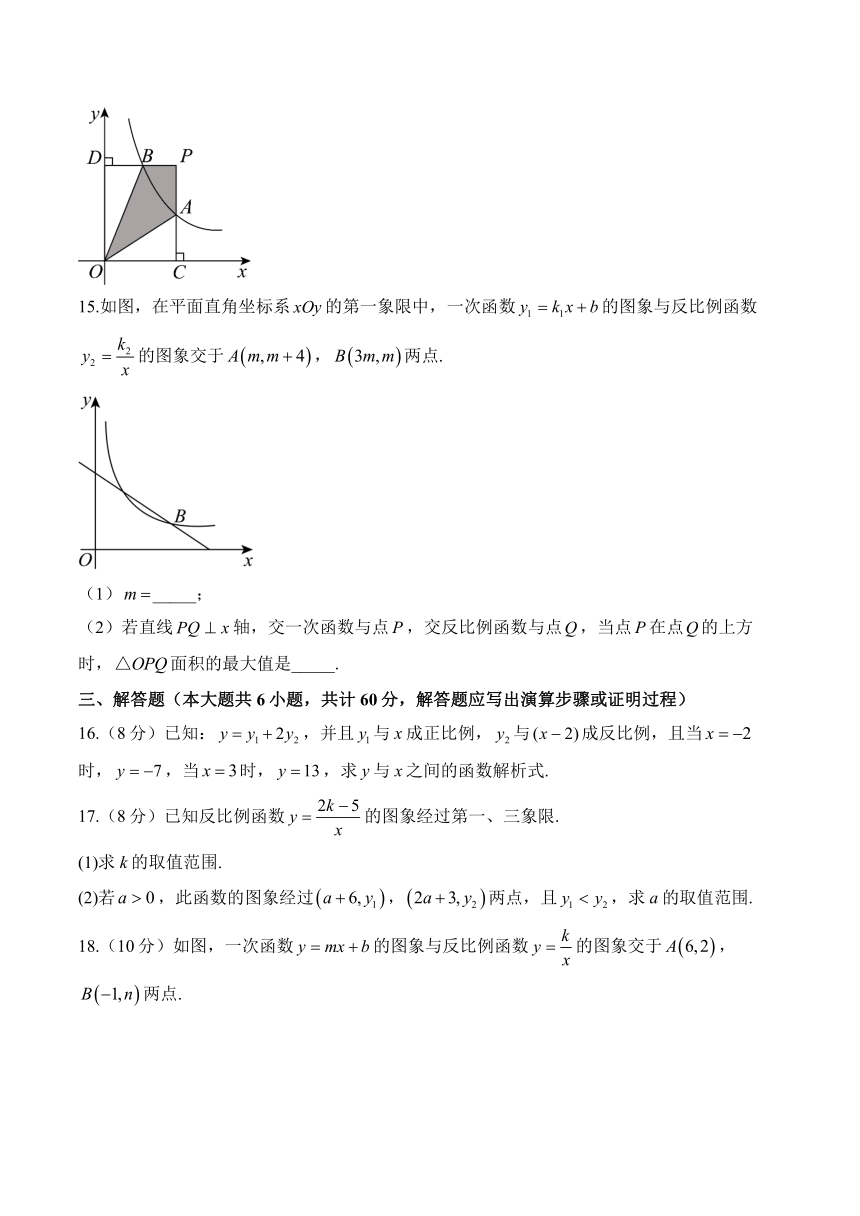
14.如图,过点作轴,垂足为C,轴,垂足为D.,分别交反比例函数()的图象于点A,B,则阴影部分的面积是________.
15.如图,在平面直角坐标系的第一象限中,一次函数的图象与反比例函数的图象交于,两点.
(1)_____;
(2)若直线轴,交一次函数与点,交反比例函数与点,当点在点的上方时,面积的最大值是_____.
三、解答题(本大题共6小题,共计60分,解答题应写出演算步骤或证明过程)
16.(8分)已知:,并且与x成正比例,与成反比例,且当时,,当时,,求y与x之间的函数解析式.
17.(8分)已知反比例函数的图象经过第一、三象限.
(1)求k的取值范围.
(2)若,此函数的图象经过,两点,且,求a的取值范围.
18.(10分)如图,一次函数的图象与反比例函数的图象交于,两点.
(1)求反比例函数的解析式;
(2)求n的值及一次函数的解析式.
19.(10分)小明发现用吸管吹气,能发出不同的音调.通过查阅资料,他得知:用吸管吹气时,吸管内部的空气振动导致声音产生,而吸管的长度影响了空气振动的频率,并最终决定了音调的不同,所以发出不同的音调.
小明和同学动手试验,并按以下步骤操作:①将若干根同规格的吸管剪成不同的长度;②用同样的力气通过吸管吹气,借助仪器记录下吸管中空气振动的频率;③将吸管的长度和相应吸管中空气振动的频率分别记为和,对收集到的数据检查、整理;④将整理所得的数据对应的点在平面直角坐标系中描出,绘制成如图所示的与对应关系的散点图.
(1)表1记录了收集到的四组数据,同学们在仔细检查、整理数据时,发现这四组数据中的一组有错,请直接写出有出错的这组数据______(填写组别代号),不必说明理由;
(表1)
数据组别 A B C D
吸管的长度 60 80 100 100
空气振动的频率 1.43 1.08 0.86 0.42
(2)根据散点图,同学们猜想y与x的对应关系符合初中阶段已学过的一种函数关系,并将由每组数据计算所得的系数(精确到个位)作为y与x的对应关系中的系数.小明根据表2的数据剪出合适长度的吸管,成功地吹奏出的音.
(表2)
音调
频率 026 0.29 033 0.35 0.39 0.44 0.49
你知道小明剪出的吸管长度是多少(精确到个位)?并说明你的理由.
20.(12分)如图,已知点、在反比例函数的图象上,过点A的一次函数的图象与y轴交于点.
(1)求m、n的值和一次函数的表达式;
(2)连结AB,求点C到线段AB的距离.
21.(12分)如图,点,在反比例函数的图象上,轴于点D,轴于点C,.
(1)求m,n的值及反比例函数的表达式.
(2)连接,在线段上是否存在点E,使的面积等于3,若存在,请求出点E的坐标;若不存在,请说明理由.
(3)若P是y轴上的一个动点,请直接写出当的周长最小时点P的坐标.
答案以及解析
1.答案:C
解析:函数中,自变量的取值范围是.
故选:C.
2.答案:D
解析:∵反比例函数的图象经过点,∴,
A、,不合题意;
B、,不合题意;
C、,不合题意;
D、,符合题意;
故选:D.
3.答案:D
解析:点在反比例函数的图象上,
,
,
,
故选:D.
4.答案:A
解析:∵每个象限内y都随x的增大而增大,
∴反比例函数图象分布在二四象限,
A.∵,∴符合题意;
B.∵,∴不符合题意;
C.∵,∴不符合题意;
D.∵在坐标轴上,不在二四象限,∴不符合题意;
故选A.
5.答案:D
解析:A、当时,则,此时一次函数经过一、三、四象限,反比例函数经过二、四象限,故选项不正确,不符合题意;
B、因为一次函数,则其与y轴交点为,故选项不正确,不符合题意;
C、因为一次函数,则其与y轴交点为,故选项不正确,不符合题意;
D、当时,则,此时一次函数经过一、三、四象限,反比例函数经过二、四象限,故选项正确,符合题意.
故选D.
6.答案:B
解析:,,,
A为反比例函数图象上一点,
,
,
故选:B.
7.答案:D
解析:A、在中,当时,,则图象不经过,原说法错误,不符合题意;
B、,
图象位于二、四象限,原说法错误,不符合题意;
C、,
图象位于二、四象限,在每个象限内y随x的增大而增大,原说法错误,不符合题意;
D、如果点在它的图象上,则,则点也在它的图象上,原说法正确,符合题意;
故选:D.
8.答案:C
解析:设,
把代入上式得,,所以,所以,故选项A正确,不符合题意;
当时,,故选项B正确,不符合题意;
由图象可得,当时,,故选项C不正确,符合题意;
当时,,时,,所以时,,故选项D正确,不符合题意.
故选:C.
9.答案:B
解析:
反比例函数图像的两个分支分别在一、三象限,在每个象限内,y随x的增大而减小,
,
,或,,
假设,且,则,
,,
,
同理:当,且时,.
故选B.
10.答案:A
解析:过点D作于F,
由已知,,
四边形ABCD是菱形,
,,
设,则,
,,,
在中,,
,
解得,(舍去),
,,
设,
则点D坐标为,点C坐标为,
点D、C在双曲线上,
,
,
,
故选:A.
11.答案:
解析:∵反比例函数的图象位于第二、四象限,
∴,解得,
故答案为:.
12.答案:1200
解析:设,
∵图像经过点,
∴,解得,
∴
把代入可得.
故答案为:1200.
13.答案:2
解析:反比例函数的图象经过点和,
,,
又,
,
即;
即m的值为2.
故答案为:2.
14.答案:6
解析:点,
,,
.
反比例函数,
,
.
故答案为:6.
15.答案:2;2
解析:(1),都在反比例函数上
解得(舍弃);
(2)如图
一次函数的解析式为
反比例函数的解析式为
设
当时,有最大值为2.
16.答案:
解析:与x成正比例,与成反比例,
设,,
,
当时,,当时,,
,解得,
y与x之间的函数解析式为.
17.答案:(1)
(2)
解析:(1)反比例函数的图象经过第一、三象限,
,解得,
的取值范围是.
(2),
,,
反比例函数的图象经过,两点,且,
,
解得,
a的取值范围是.
18.答案:(1)
(2),
解析:(1)反比例函数的图象过点,
,
解得,
反比例函数的解析式为;
(2)反比例函数的图象过点,
,
解得,
,
一次函数的图象与反比例函数的图象交于,,
,解得,
一次函数的解析式为.
19.答案:(1)D
(2),理由见解析
解析:(1)根据表中数据,可发现y与x的乘积为定值,
所以D组数据是错误的,
故答案为:D.
(2)根据散点图判断,可以用反比例函数来确定y与x的对应关系,
因此可设.
依据表1中A,B,C三组数据求得:
,
,
.
,
,
当时,.
答:小明剪出的吸管长度是.
20.答案:(1)
(2)
解析:(1)点、在反比例函数图象上,
,.
又一次函数过点,,
解得,
一次函数表达式为.
(2)如图,连结BC.
过点A作,垂足为点D,过点C作,垂足为点E.
,,轴,.
点,,,
点,,.
在中,.
又,
即,
,即点C到线段AB的距离为.
21.答案:(1),,
(2)存在,
(3)
解析:(1)点,在反比例函数的图象上,
,
即,
,
,
,,
点,点,
,
反比例函数的表达式为;
(2)设点,
,,,,
,
,
点;
(3)的周长,
又是定值,
当的值最小是,的周长最小,
如图,作点B关于y轴的对称点,连接交y轴于点P,此时有最小值,
设直线的解析式为,
,
解得,
直线的解析式为,
当时,,
点.
【满分:120】
一、选择题:(本大题共10小题,每小题4分,共40分,给出的四个选项中,只有一项是符合题目要求的)
1.函数中,自变量的取值范围是( )
A. B. C. D.全体实数
2.若反比例函数的图象经过点,则该函数图象一定经过( )
A. B. C. D.
3.如果点在反比例函数的图象上,则代数式的值为( )
A.0 B. C.2 D.
4.对于反比例函数,在每个象限内y都随x的增大而增大,则下列点可能在这个函数图象上的为( )
A. B. C. D.
5.反比例函数与一次函数在同一平面直角坐标系中的图象大致是( )
A. B. C. D.
6.如图是反比例函数的图象,点是反比例函数图象上任意一点,过点A作轴于点B,连接,则的面积是( )
A.2 B.1 C. D.
7.已知反比例函数,则下列描述正确的是( )
A.图象必经过
B.图象位于一、三象限
C.y随x的增大而增大
D.如果点在它的图象上,则点也在它的图象上
8.密闭容器内有一定质量的二氧化碳,当容器的体积V(单位:)变化时,气体的密度(单位:随之变化.已知密度与体积V是反比例函数关系,它的图象如图所示,当时,.根据图象可知,下列说法不正确的是( )
A.与V的函数关系式是
B.当时,
C.当时,
D.当时,的变化范围是
9.已知点,在反比例函数(k为常数)图像上,.若,则的值为( ).
A.0 B.负数 C.正数 D.非负数
10.如图,在平面直角坐标系中,菱形ABCD的边轴,垂足为E,顶点A在第二象限,顶点B在y轴正半轴上,反比例函数的图象同时经过顶点C、D.若点C的横坐标为5,,则k的值为( )
A. B. C. D.
二、填空题(每小题4分,共20分)
11.已知反比例函数的图象位于第二、第四象限,则k的取值范围为______.
12.在物理学中,功率表示做功的快慢,功与做功时间的比叫做功率,即所做的功一定时,功率与做功所用的时间成反比例函数关系,图象如图所示,当时,________.
13.在平面直角坐标系中,反比例函数的图象经过点和,若,则m的值为______.
14.如图,过点作轴,垂足为C,轴,垂足为D.,分别交反比例函数()的图象于点A,B,则阴影部分的面积是________.
15.如图,在平面直角坐标系的第一象限中,一次函数的图象与反比例函数的图象交于,两点.
(1)_____;
(2)若直线轴,交一次函数与点,交反比例函数与点,当点在点的上方时,面积的最大值是_____.
三、解答题(本大题共6小题,共计60分,解答题应写出演算步骤或证明过程)
16.(8分)已知:,并且与x成正比例,与成反比例,且当时,,当时,,求y与x之间的函数解析式.
17.(8分)已知反比例函数的图象经过第一、三象限.
(1)求k的取值范围.
(2)若,此函数的图象经过,两点,且,求a的取值范围.
18.(10分)如图,一次函数的图象与反比例函数的图象交于,两点.
(1)求反比例函数的解析式;
(2)求n的值及一次函数的解析式.
19.(10分)小明发现用吸管吹气,能发出不同的音调.通过查阅资料,他得知:用吸管吹气时,吸管内部的空气振动导致声音产生,而吸管的长度影响了空气振动的频率,并最终决定了音调的不同,所以发出不同的音调.
小明和同学动手试验,并按以下步骤操作:①将若干根同规格的吸管剪成不同的长度;②用同样的力气通过吸管吹气,借助仪器记录下吸管中空气振动的频率;③将吸管的长度和相应吸管中空气振动的频率分别记为和,对收集到的数据检查、整理;④将整理所得的数据对应的点在平面直角坐标系中描出,绘制成如图所示的与对应关系的散点图.
(1)表1记录了收集到的四组数据,同学们在仔细检查、整理数据时,发现这四组数据中的一组有错,请直接写出有出错的这组数据______(填写组别代号),不必说明理由;
(表1)
数据组别 A B C D
吸管的长度 60 80 100 100
空气振动的频率 1.43 1.08 0.86 0.42
(2)根据散点图,同学们猜想y与x的对应关系符合初中阶段已学过的一种函数关系,并将由每组数据计算所得的系数(精确到个位)作为y与x的对应关系中的系数.小明根据表2的数据剪出合适长度的吸管,成功地吹奏出的音.
(表2)
音调
频率 026 0.29 033 0.35 0.39 0.44 0.49
你知道小明剪出的吸管长度是多少(精确到个位)?并说明你的理由.
20.(12分)如图,已知点、在反比例函数的图象上,过点A的一次函数的图象与y轴交于点.
(1)求m、n的值和一次函数的表达式;
(2)连结AB,求点C到线段AB的距离.
21.(12分)如图,点,在反比例函数的图象上,轴于点D,轴于点C,.
(1)求m,n的值及反比例函数的表达式.
(2)连接,在线段上是否存在点E,使的面积等于3,若存在,请求出点E的坐标;若不存在,请说明理由.
(3)若P是y轴上的一个动点,请直接写出当的周长最小时点P的坐标.
答案以及解析
1.答案:C
解析:函数中,自变量的取值范围是.
故选:C.
2.答案:D
解析:∵反比例函数的图象经过点,∴,
A、,不合题意;
B、,不合题意;
C、,不合题意;
D、,符合题意;
故选:D.
3.答案:D
解析:点在反比例函数的图象上,
,
,
,
故选:D.
4.答案:A
解析:∵每个象限内y都随x的增大而增大,
∴反比例函数图象分布在二四象限,
A.∵,∴符合题意;
B.∵,∴不符合题意;
C.∵,∴不符合题意;
D.∵在坐标轴上,不在二四象限,∴不符合题意;
故选A.
5.答案:D
解析:A、当时,则,此时一次函数经过一、三、四象限,反比例函数经过二、四象限,故选项不正确,不符合题意;
B、因为一次函数,则其与y轴交点为,故选项不正确,不符合题意;
C、因为一次函数,则其与y轴交点为,故选项不正确,不符合题意;
D、当时,则,此时一次函数经过一、三、四象限,反比例函数经过二、四象限,故选项正确,符合题意.
故选D.
6.答案:B
解析:,,,
A为反比例函数图象上一点,
,
,
故选:B.
7.答案:D
解析:A、在中,当时,,则图象不经过,原说法错误,不符合题意;
B、,
图象位于二、四象限,原说法错误,不符合题意;
C、,
图象位于二、四象限,在每个象限内y随x的增大而增大,原说法错误,不符合题意;
D、如果点在它的图象上,则,则点也在它的图象上,原说法正确,符合题意;
故选:D.
8.答案:C
解析:设,
把代入上式得,,所以,所以,故选项A正确,不符合题意;
当时,,故选项B正确,不符合题意;
由图象可得,当时,,故选项C不正确,符合题意;
当时,,时,,所以时,,故选项D正确,不符合题意.
故选:C.
9.答案:B
解析:
反比例函数图像的两个分支分别在一、三象限,在每个象限内,y随x的增大而减小,
,
,或,,
假设,且,则,
,,
,
同理:当,且时,.
故选B.
10.答案:A
解析:过点D作于F,
由已知,,
四边形ABCD是菱形,
,,
设,则,
,,,
在中,,
,
解得,(舍去),
,,
设,
则点D坐标为,点C坐标为,
点D、C在双曲线上,
,
,
,
故选:A.
11.答案:
解析:∵反比例函数的图象位于第二、四象限,
∴,解得,
故答案为:.
12.答案:1200
解析:设,
∵图像经过点,
∴,解得,
∴
把代入可得.
故答案为:1200.
13.答案:2
解析:反比例函数的图象经过点和,
,,
又,
,
即;
即m的值为2.
故答案为:2.
14.答案:6
解析:点,
,,
.
反比例函数,
,
.
故答案为:6.
15.答案:2;2
解析:(1),都在反比例函数上
解得(舍弃);
(2)如图
一次函数的解析式为
反比例函数的解析式为
设
当时,有最大值为2.
16.答案:
解析:与x成正比例,与成反比例,
设,,
,
当时,,当时,,
,解得,
y与x之间的函数解析式为.
17.答案:(1)
(2)
解析:(1)反比例函数的图象经过第一、三象限,
,解得,
的取值范围是.
(2),
,,
反比例函数的图象经过,两点,且,
,
解得,
a的取值范围是.
18.答案:(1)
(2),
解析:(1)反比例函数的图象过点,
,
解得,
反比例函数的解析式为;
(2)反比例函数的图象过点,
,
解得,
,
一次函数的图象与反比例函数的图象交于,,
,解得,
一次函数的解析式为.
19.答案:(1)D
(2),理由见解析
解析:(1)根据表中数据,可发现y与x的乘积为定值,
所以D组数据是错误的,
故答案为:D.
(2)根据散点图判断,可以用反比例函数来确定y与x的对应关系,
因此可设.
依据表1中A,B,C三组数据求得:
,
,
.
,
,
当时,.
答:小明剪出的吸管长度是.
20.答案:(1)
(2)
解析:(1)点、在反比例函数图象上,
,.
又一次函数过点,,
解得,
一次函数表达式为.
(2)如图,连结BC.
过点A作,垂足为点D,过点C作,垂足为点E.
,,轴,.
点,,,
点,,.
在中,.
又,
即,
,即点C到线段AB的距离为.
21.答案:(1),,
(2)存在,
(3)
解析:(1)点,在反比例函数的图象上,
,
即,
,
,
,,
点,点,
,
反比例函数的表达式为;
(2)设点,
,,,,
,
,
点;
(3)的周长,
又是定值,
当的值最小是,的周长最小,
如图,作点B关于y轴的对称点,连接交y轴于点P,此时有最小值,
设直线的解析式为,
,
解得,
直线的解析式为,
当时,,
点.
