第2章 解直角三角形单元测试(B卷提升篇)(含解析)
文档属性
| 名称 | 第2章 解直角三角形单元测试(B卷提升篇)(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-15 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
青岛版9上数学第2章解直角三角形单元测试( B卷提升篇)(含解析)
学校:___________姓名:___________班级:___________考号:___________
注意事项:
1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡对应题目的答案标号涂黑;如需改动,用橡皮擦干净后,再选涂其他答案标号。回答非选择题时,将答案写在答题卡上,写在试卷上无效。
3.考试结束后,本试卷和答题卡一并交回。
第I卷(选择题)
一、选择题:本题共10小题,每小题3分,共30分。在每小题给出的选项中,只有一项是符合题目要求的。
1.三角函数、、之间的大小关系是( )
A. B.
C. D.
2.点P的坐标为,A是x轴正半轴上一点,O为原点,则的值为( )
A. 3 B. C. D.
3.如图,圆规两脚OA,OB张开的角度为,,则两脚张开的距离AB为( )
A. B. C. D.
4.如图,点A为边上的任意一点,作于点C,于点D,下列用线段比表示的值,错误的是( )
A. B. C. D.
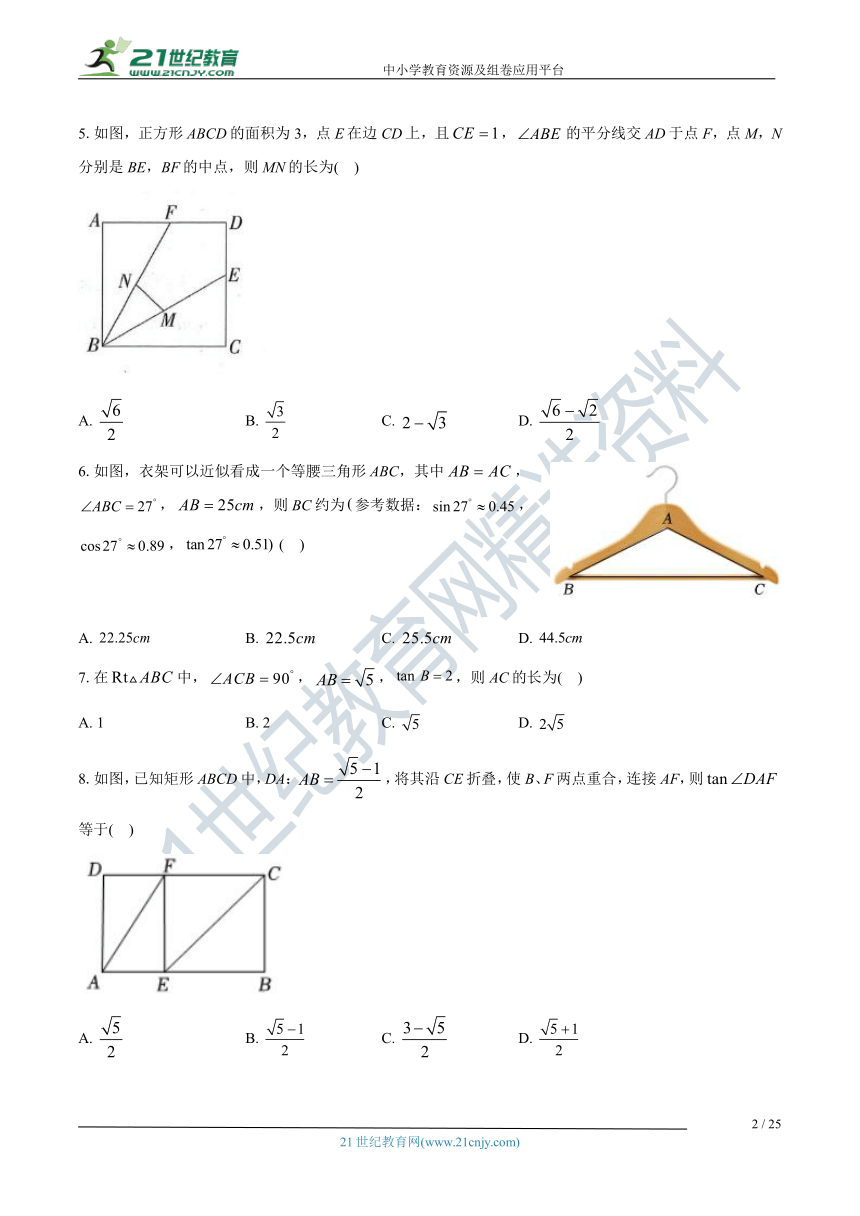
5.如图,正方形ABCD的面积为3,点E在边CD上,且,的平分线交AD于点F,点M,N分别是BE,BF的中点,则MN的长为( )
A. B. C. D.
6.如图,衣架可以近似看成一个等腰三角形ABC,其中,,,则BC约为参考数据:,, ( )
A. B. C. D.
7.在中,,,,则AC的长为( )
A. 1 B. 2 C. D.
8.如图,已知矩形ABCD中,DA:,将其沿CE折叠,使B、F两点重合,连接AF,则等于( )
A. B. C. D.
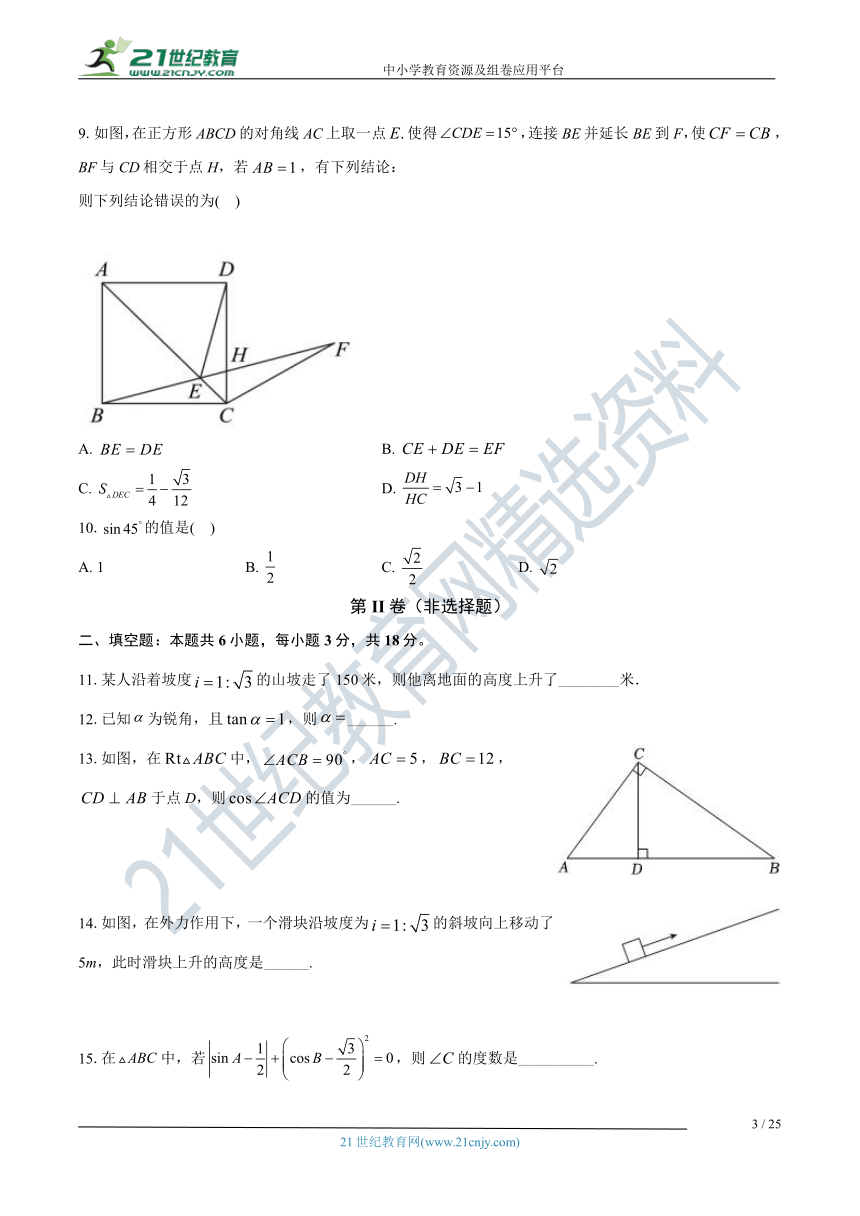
9.如图,在正方形ABCD的对角线AC上取一点使得,连接BE并延长BE到F,使,BF与CD相交于点H,若,有下列结论:
则下列结论错误的为( )
A. B.
C. D.
10.的值是( )
A. 1 B. C. D.
第II卷(非选择题)
二、填空题:本题共6小题,每小题3分,共18分。
11.某人沿着坡度的山坡走了150米,则他离地面的高度上升了________米.
12.已知为锐角,且,则______.
13.如图,在中,,,,于点D,则的值为______.
14.如图,在外力作用下,一个滑块沿坡度为的斜坡向上移动了5m,此时滑块上升的高度是______.
15.在中,若,则的度数是__________.
16.如图,在中,,,D是BC的中点,,则AB的长为__________.
三、解答题:本题共8小题,共74分。解答应写出文字说明,证明过程或演算步骤。
17.本小题6分
计算:;
化简:
18.本小题6分
如图,一艘渔船位于小岛B的北偏东方向,距离小岛20千米的点A处,它沿着点A的南偏东的方向航行.
填空:______度,______度;
渔船航行多远时距离小岛B最近?结果保留根号
渔船到达距离小岛B最近点后,按原航向继续航行千米到点C处时突然发生事故,渔船马上向小岛B上的救援队求救,问救援队从B处出发沿着哪个方向航行到达事故地点航程最短,最短航程是多少?结果精确到1千米,参考数据,,
19.本小题8分
如图,五边形ABCDE是某公园的游览步道,把公园的五个景点连接起来,为方便游览,增设了步道经勘测,,景点C在景点A的东北方向,且在景点B的南偏东方向的800米处,景点D在景点C的正南方向500米处,参考数据:,
求景点A与景点E的距离;结果精确到1米
甲、乙两人同时从景点A出发,选择相反的路线依次游览其余四个景点,最后回到景点A,两人在各景点处停留时间忽略不计.其中甲的游览路线是,甲游览的平均速度是100米/分,乙游览的平均速度是80米/分.请通过计算说明在游览过程中,甲、乙谁先到达景点C?
20.本小题8分
如图,某商场开业之际,为了美化和宣传,该商场在楼上悬挂一块长为3m的宣传牌,即数学小组的同学要在双休日测量宣传牌的底部点D到地面的距离.根据所学的相关知识,他们分别在点A和点B处放置两个测倾仪,它们的高度是,站在点A处的同学测得宣传牌底部点D的仰角为,站在点B处的同学测得宣传牌顶部点C的仰角为,依据他们测量的数据能否求出宣传牌底部点D到地面的距离DH的长?若能,请求出;若不能,请说明理由图中点A,B,C,D,E,F,H在同一平面内.参考数据:,,
21.本小题10分
北斗卫星导航系统是中国自行研制的卫星导航系统,其由空间段,地面段和用户段三部分组成,可在全球范围内全天候、全天时为各类用户提供高精度、高可靠定位、导航、授时服务.如图,小敏一家自驾到风景区C游玩,到达A地后,导航显示车辆应沿北偏西方向行驶4千米至B地,再沿北偏东方向行驶一段距离到达风景区C,小敏发现风景区C在A地的北偏东方向.
求的度数;
求A、C两地的距离如果运算结果有根号,请保留根号
22.本小题12分
为了增强学生体质、锤炼学生意志,某校组织一次定向越野拉练活动.如图,A为出发点,途中设置两个检查点,分别为B,C,行进路线为检查点B在出发点A的南偏东方向上的处,检查点C在出发点A的北偏东方向上,行进路线AB和BC所在直线的夹角为求:
行进路线BC和CA所在直线的夹角的度数;
检查点B,C之间的距离结果保留根号
23.本小题12分
如图,小睿为测量公园的一凉亭AB的高度,他先在水平地面点E处用高的测角仪DE测得,然后沿EB方向向前走4m到达点G处,在点G处用高的测角仪FG测得求凉亭AB的高度.三点共线,,,,结果精确到参考数据:,,,,,
24.本小题12分
某数学兴趣小组借助无人机测量一条河流的宽度如图所示,一架水平飞行的无人机在A处测得河流左岸C处的俯角为,无人机沿水平线AF方向继续飞行12米至B处,测得河流右岸D处的俯角为,线段米为无人机距地面的铅直高度,点M,C,D在同一条直线上,其中求河流的宽度结果精确到1米,参考数据:
答案和解析
1.【答案】C
【解析】解:,
正弦函数是增函数,函数值随角度的增大而增大,
,
即
故选:
先根据正弦和余弦之间的关系把其中的变换成正弦函数,然后根据锐角三角函数的增减性判断几个三角函数值的大小即可解决问题.
本题主要考查三角函数的增减性和正弦余弦之间的关系,深入理解题意是解决问题的关键.
2.【答案】B
【解析】解:过点P作,垂足为B,如图:
,
,,
,
,
故选:
过点P作,垂足为B,在中,利用勾股定理求出OP的长,然后利用锐角三角函数的定义进行计算可解答.
本题考查了解直角三角形,坐标与图形性质,根据题目的已知条件画出图形进行分析是解题的关键.
3.【答案】C
【解析】【分析】
本题主要考查解直角三角形的应用,等腰三角形的性质.
作于点C,得出,,,再解直角三角形即可.
【解答】
解:如图:作于点C,
,,
,,,
,
,
4.【答案】C
【解析】解:,,
,
,
,
选项A、B、D不符合题意,选项C符合题意;
故选:
证出,进而利用锐角三角函数关系得出答案.
此题主要考查了锐角三角函数的定义,得出是解题关键.
5.【答案】D
【解析】如图,连接EF,
正方形ABCD的面积为3,
,,
,,
平分,
在中,,
,
,又,
是等腰直角三角形,
,N分别是BE,BF的中点,
是的中位线,
故选
6.【答案】D
【解析】解:过点A作,垂足为D,
在中,,,
,
,,
,
约为,
故选:
过点A作,垂足为D,在中,利用锐角三角函数的定义求出BD的长,然后利用等腰三角形的三线合一性质进行计算,即可解答.
本题考查了解直角三角形的应用,等腰三角形的性质,根据题目的已知条件并结合图形添加适当的辅助线是解题的关键.
7.【答案】B
【解析】【分析】
本题考查的是锐角三角函数的定义、勾股定理,掌握锐角A的对边a与邻边b的比叫做的正切是解题的关键.根据正切的定义得到,根据勾股定理列式计算即可.
【解答】
解:在中,,,
,
,
由勾股定理得,,即,
解得,
故选
8.【答案】B
【解析】解:在矩形ABCD中,,,,
:,
设,则,
,
由折叠可知:,
,
在中,
故选:
设,则,根据矩形性质可得,由折叠可得,所以,然后利用正切定义即可解决问题.
本题考查了翻折变换,矩形的性质,正切定义,解决本题的关键是掌握翻折的性质.
9.【答案】D
【解析】【分析】
此题考查正方形的性质、全等三角形的判定与性质、相似三角形的判定与性质、锐角三角函数,解直角三角形等知识,此题难度较大,应注意检验结果的正确性.
连接BD交AC于点O,由正方形的性质可得AC垂直平分BD,则,可判断A;在EF上截取,连接CG,则是等边三角形,证明≌,可证明,则,可判断B;由可求得,可判断C;通过证明得∽,则可以求得,可判断
【解答】
解:如图,连接BD交AC于点O,
四边形ABCD是正方形,
垂直平分BD,
,故A正确;
,,
,
,
,
,
,,又,
≌,
,
,
,
,
在EF上截取,连接CG,则是等边三角形,
,,
,
,
≌,
,
,故B正确;
,,
,
,,
,
,
,
,
,故C正确;
,
,
,
,
∽,
,,
,故D错误,
故选:
10.【答案】C
【解析】解:由特殊角的三角函数值可知,
故选:
直接根据特殊角的三角函数值进行解答即可.
本题考查的是特殊角的三角函数值,熟记各特殊角度的三角函数值是解答此题的关键.
11.【答案】
【解析】【分析】根据题意可以设出某人沿着坡度的山坡走了150米时的竖直高度,然后根据勾股定理即可解答本题.
【详解】解:设某人沿着坡度的山坡走了150米时的竖直高度为x米,
则此时走的水平距离为米,
由勾股定理可得,,
解得,负值已舍去,
故答案为:
本题考查解直角三角形的应用-坡度坡角问题、勾股定理,明确坡度的含义是解答此类题目的关键.
12.【答案】
【解析】解:为锐角,且,
故答案为:
由特殊角的正切值,即可得到答案.
本题考查特殊角的三角函数值,关键是熟记特殊角的三角函数值.
13.【答案】
【解析】解:在中,,,,
,
,,
,,
,
故答案为:
首先在中利用勾股定理求出AB,再根据同角的余角相等得出,进而利用锐角三角函数关系即可求出的值.
此题主要考查了锐角三角函数关系的定义,得出是解题关键.
14.【答案】
【解析】解:斜坡AB的坡度:,
,
,
,
故答案为:
根据坡度的概念求出,再根据正弦的定义计算即可.
本题考查的是解直角三角形的应用-坡度坡角问题,熟记坡度是坡面的铅直高度h和水平宽度l的比是解题的关键.
15.【答案】
【解析】解:,
,,
,,
,,
,
故答案为:
根据绝对值和偶次方的非负性可得,,从而可得,,然后利用特殊角的三角函数值可得,,最后利用三角形内角和定理进行计算即可解答.
本题考查了特殊角的三角函数值,绝对值和偶次方的非负性,熟练掌握特殊角的三角函数值是解题的关键.
16.【答案】
【解析】略
17.【答案】解:原式
;
原式
【解析】先根据负整数指数幂,特殊角的三角函数值,二次根式的性质,零指数幂进行计算,再算加减即可;
先算括号内的加法,再把除法变成乘法,最后算乘法即可.
本题考查了零指数幂,负整数指数幂,实数的混合运算,特殊角的三角函数值,分式的混合运算等知识点,能正确运用实数和分式的运算法则进行计算是解此题的关键,注意运算顺序.
18.【答案】60 45
【解析】解:如图:
由题意得:,,,
,
,
由题意得:,
,
故答案为:60;45;
过点B作,垂足为G,
在中,,,
,
渔船航行时,距离小岛B最近;
如图:
在中,,,
,,
由题意得:,
在中,,
,
,
,
,
救援队从B处出发沿着南偏东方向航行到达事故地点航程最短,最短航程约为
根据题意可得:,,,从而可得,进而可得,然后再根据题意可得:,从而利用角的和差关系可得,即可解答;
过点B作,垂足为G,在中,利用锐角三角函数的定义求出AG的长,即可解答;
先在中,求出BG的长和的度数,再根据题意可得:,从而在中,利用锐角三角函数的定义求出,然后根据特殊角的三角函数值可得,再利用锐角三角函数的定义求出BC的长,最后利用平角定义求出的度数,即可解答.
本题考查了解直角三角形的应用-方向角问题,根据题目的已知条件并结合图形添加适当的辅助线是解题的关键.
19.【答案】解:延长AE,CD交于点G,连接AC,过点C作于点F,如图,
由题意得:米,米,,
景点C在景点A的东北方向,
在中,
,
,
米,米
,,
米,
米,
,,
米,
米,
,
,
米,
米,
米
答:景点A与景点E的距离359米.
乙先到达景点C,理由:
由知:米,
米,
甲到达点C所有的时间为分,
乙到达点C所有的时间为分,
,
乙先到达景点
【解析】延长AE,CD交于点G,连接AC,过点C作于点F,利用含角的直角三角形的性质,等腰直角三角形的性质解答即可;
利用的结论分别计算出甲,乙两人的走的路程,再计算出到达点C的时间即可.
本题主要考查了直角三角形的应用,含角的直角三角形的性质,等腰直角三角形的性质,勾股定理,方向角,近似数和有效数字,恰当的构造直角三角形是解题的关键.
20.【答案】解:能,理由如下:
延长EF交CH于N,如图所示:
则,
,
,
设,则,
,
在中,,
,
,
解得:,
,
答:点D到地面的距离DH的长约为
【解析】延长EF交CH于N,根据等腰直角三角形的性质得到,根据正切的定义求出DN,结合图形计算即可.
本题考查了解直角三角形的应用-仰角俯角问题,掌握仰角俯角的概念、熟记锐角三角函数的定义是解题的关键.
21.【答案】解:由题意得,,,
过点B作于点D,
,
,
,
千米,
在中,,
解得,
,
千米,
千米.
答:A、C两地的距离为千米.
【解析】由题意得,,则
过点B作于点D,在中,可得千米,千米,在中,可得千米,根据可得答案.
本题考查解直角三角形的应用-方向角问题,熟练掌握锐角三角函数的定义是解答本题的关键.
22.【答案】【小题1】
由题意,得,,
,
行进路线BC和CA所在直线的夹角的度数为
【小题2】
如图,过点A作,垂足为
在中,,,
,
在中,,
检查点B,C之间的距离为
【解析】见答案
见答案
23.【答案】解:由题意得:
,,,
设,
,
在中,,
,
在中,,
,
,
解得,
,
凉亭AB的高约为
【解析】本题考查了解直角三角形的应用-仰角俯角问题,熟练掌握锐角三角函数的定义是解题的关键.根据题意可得,,,然后设,则,在和中,利用锐角三角函数的定义分别求出AC的长,从而列出关于x的方程,进行计算即可解答.
24.【答案】解:过点B作于点则四边形AMEB是矩形.
,米,
,
在中,,
,
,
米,
在中,,,
,
,
米,
米
答:河流的宽度CD约为64米.
【解析】过点B作于点E,分别解、即可.
本题考查了关于俯仰角的解直角三角形的问题,作垂线构造直角三角形是解答本题的关键.
21世纪教育网(www.21cnjy.com)
青岛版9上数学第2章解直角三角形单元测试( B卷提升篇)(含解析)
学校:___________姓名:___________班级:___________考号:___________
注意事项:
1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡对应题目的答案标号涂黑;如需改动,用橡皮擦干净后,再选涂其他答案标号。回答非选择题时,将答案写在答题卡上,写在试卷上无效。
3.考试结束后,本试卷和答题卡一并交回。
第I卷(选择题)
一、选择题:本题共10小题,每小题3分,共30分。在每小题给出的选项中,只有一项是符合题目要求的。
1.三角函数、、之间的大小关系是( )
A. B.
C. D.
2.点P的坐标为,A是x轴正半轴上一点,O为原点,则的值为( )
A. 3 B. C. D.
3.如图,圆规两脚OA,OB张开的角度为,,则两脚张开的距离AB为( )
A. B. C. D.
4.如图,点A为边上的任意一点,作于点C,于点D,下列用线段比表示的值,错误的是( )
A. B. C. D.
5.如图,正方形ABCD的面积为3,点E在边CD上,且,的平分线交AD于点F,点M,N分别是BE,BF的中点,则MN的长为( )
A. B. C. D.
6.如图,衣架可以近似看成一个等腰三角形ABC,其中,,,则BC约为参考数据:,, ( )
A. B. C. D.
7.在中,,,,则AC的长为( )
A. 1 B. 2 C. D.
8.如图,已知矩形ABCD中,DA:,将其沿CE折叠,使B、F两点重合,连接AF,则等于( )
A. B. C. D.
9.如图,在正方形ABCD的对角线AC上取一点使得,连接BE并延长BE到F,使,BF与CD相交于点H,若,有下列结论:
则下列结论错误的为( )
A. B.
C. D.
10.的值是( )
A. 1 B. C. D.
第II卷(非选择题)
二、填空题:本题共6小题,每小题3分,共18分。
11.某人沿着坡度的山坡走了150米,则他离地面的高度上升了________米.
12.已知为锐角,且,则______.
13.如图,在中,,,,于点D,则的值为______.
14.如图,在外力作用下,一个滑块沿坡度为的斜坡向上移动了5m,此时滑块上升的高度是______.
15.在中,若,则的度数是__________.
16.如图,在中,,,D是BC的中点,,则AB的长为__________.
三、解答题:本题共8小题,共74分。解答应写出文字说明,证明过程或演算步骤。
17.本小题6分
计算:;
化简:
18.本小题6分
如图,一艘渔船位于小岛B的北偏东方向,距离小岛20千米的点A处,它沿着点A的南偏东的方向航行.
填空:______度,______度;
渔船航行多远时距离小岛B最近?结果保留根号
渔船到达距离小岛B最近点后,按原航向继续航行千米到点C处时突然发生事故,渔船马上向小岛B上的救援队求救,问救援队从B处出发沿着哪个方向航行到达事故地点航程最短,最短航程是多少?结果精确到1千米,参考数据,,
19.本小题8分
如图,五边形ABCDE是某公园的游览步道,把公园的五个景点连接起来,为方便游览,增设了步道经勘测,,景点C在景点A的东北方向,且在景点B的南偏东方向的800米处,景点D在景点C的正南方向500米处,参考数据:,
求景点A与景点E的距离;结果精确到1米
甲、乙两人同时从景点A出发,选择相反的路线依次游览其余四个景点,最后回到景点A,两人在各景点处停留时间忽略不计.其中甲的游览路线是,甲游览的平均速度是100米/分,乙游览的平均速度是80米/分.请通过计算说明在游览过程中,甲、乙谁先到达景点C?
20.本小题8分
如图,某商场开业之际,为了美化和宣传,该商场在楼上悬挂一块长为3m的宣传牌,即数学小组的同学要在双休日测量宣传牌的底部点D到地面的距离.根据所学的相关知识,他们分别在点A和点B处放置两个测倾仪,它们的高度是,站在点A处的同学测得宣传牌底部点D的仰角为,站在点B处的同学测得宣传牌顶部点C的仰角为,依据他们测量的数据能否求出宣传牌底部点D到地面的距离DH的长?若能,请求出;若不能,请说明理由图中点A,B,C,D,E,F,H在同一平面内.参考数据:,,
21.本小题10分
北斗卫星导航系统是中国自行研制的卫星导航系统,其由空间段,地面段和用户段三部分组成,可在全球范围内全天候、全天时为各类用户提供高精度、高可靠定位、导航、授时服务.如图,小敏一家自驾到风景区C游玩,到达A地后,导航显示车辆应沿北偏西方向行驶4千米至B地,再沿北偏东方向行驶一段距离到达风景区C,小敏发现风景区C在A地的北偏东方向.
求的度数;
求A、C两地的距离如果运算结果有根号,请保留根号
22.本小题12分
为了增强学生体质、锤炼学生意志,某校组织一次定向越野拉练活动.如图,A为出发点,途中设置两个检查点,分别为B,C,行进路线为检查点B在出发点A的南偏东方向上的处,检查点C在出发点A的北偏东方向上,行进路线AB和BC所在直线的夹角为求:
行进路线BC和CA所在直线的夹角的度数;
检查点B,C之间的距离结果保留根号
23.本小题12分
如图,小睿为测量公园的一凉亭AB的高度,他先在水平地面点E处用高的测角仪DE测得,然后沿EB方向向前走4m到达点G处,在点G处用高的测角仪FG测得求凉亭AB的高度.三点共线,,,,结果精确到参考数据:,,,,,
24.本小题12分
某数学兴趣小组借助无人机测量一条河流的宽度如图所示,一架水平飞行的无人机在A处测得河流左岸C处的俯角为,无人机沿水平线AF方向继续飞行12米至B处,测得河流右岸D处的俯角为,线段米为无人机距地面的铅直高度,点M,C,D在同一条直线上,其中求河流的宽度结果精确到1米,参考数据:
答案和解析
1.【答案】C
【解析】解:,
正弦函数是增函数,函数值随角度的增大而增大,
,
即
故选:
先根据正弦和余弦之间的关系把其中的变换成正弦函数,然后根据锐角三角函数的增减性判断几个三角函数值的大小即可解决问题.
本题主要考查三角函数的增减性和正弦余弦之间的关系,深入理解题意是解决问题的关键.
2.【答案】B
【解析】解:过点P作,垂足为B,如图:
,
,,
,
,
故选:
过点P作,垂足为B,在中,利用勾股定理求出OP的长,然后利用锐角三角函数的定义进行计算可解答.
本题考查了解直角三角形,坐标与图形性质,根据题目的已知条件画出图形进行分析是解题的关键.
3.【答案】C
【解析】【分析】
本题主要考查解直角三角形的应用,等腰三角形的性质.
作于点C,得出,,,再解直角三角形即可.
【解答】
解:如图:作于点C,
,,
,,,
,
,
4.【答案】C
【解析】解:,,
,
,
,
选项A、B、D不符合题意,选项C符合题意;
故选:
证出,进而利用锐角三角函数关系得出答案.
此题主要考查了锐角三角函数的定义,得出是解题关键.
5.【答案】D
【解析】如图,连接EF,
正方形ABCD的面积为3,
,,
,,
平分,
在中,,
,
,又,
是等腰直角三角形,
,N分别是BE,BF的中点,
是的中位线,
故选
6.【答案】D
【解析】解:过点A作,垂足为D,
在中,,,
,
,,
,
约为,
故选:
过点A作,垂足为D,在中,利用锐角三角函数的定义求出BD的长,然后利用等腰三角形的三线合一性质进行计算,即可解答.
本题考查了解直角三角形的应用,等腰三角形的性质,根据题目的已知条件并结合图形添加适当的辅助线是解题的关键.
7.【答案】B
【解析】【分析】
本题考查的是锐角三角函数的定义、勾股定理,掌握锐角A的对边a与邻边b的比叫做的正切是解题的关键.根据正切的定义得到,根据勾股定理列式计算即可.
【解答】
解:在中,,,
,
,
由勾股定理得,,即,
解得,
故选
8.【答案】B
【解析】解:在矩形ABCD中,,,,
:,
设,则,
,
由折叠可知:,
,
在中,
故选:
设,则,根据矩形性质可得,由折叠可得,所以,然后利用正切定义即可解决问题.
本题考查了翻折变换,矩形的性质,正切定义,解决本题的关键是掌握翻折的性质.
9.【答案】D
【解析】【分析】
此题考查正方形的性质、全等三角形的判定与性质、相似三角形的判定与性质、锐角三角函数,解直角三角形等知识,此题难度较大,应注意检验结果的正确性.
连接BD交AC于点O,由正方形的性质可得AC垂直平分BD,则,可判断A;在EF上截取,连接CG,则是等边三角形,证明≌,可证明,则,可判断B;由可求得,可判断C;通过证明得∽,则可以求得,可判断
【解答】
解:如图,连接BD交AC于点O,
四边形ABCD是正方形,
垂直平分BD,
,故A正确;
,,
,
,
,
,
,,又,
≌,
,
,
,
,
在EF上截取,连接CG,则是等边三角形,
,,
,
,
≌,
,
,故B正确;
,,
,
,,
,
,
,
,
,故C正确;
,
,
,
,
∽,
,,
,故D错误,
故选:
10.【答案】C
【解析】解:由特殊角的三角函数值可知,
故选:
直接根据特殊角的三角函数值进行解答即可.
本题考查的是特殊角的三角函数值,熟记各特殊角度的三角函数值是解答此题的关键.
11.【答案】
【解析】【分析】根据题意可以设出某人沿着坡度的山坡走了150米时的竖直高度,然后根据勾股定理即可解答本题.
【详解】解:设某人沿着坡度的山坡走了150米时的竖直高度为x米,
则此时走的水平距离为米,
由勾股定理可得,,
解得,负值已舍去,
故答案为:
本题考查解直角三角形的应用-坡度坡角问题、勾股定理,明确坡度的含义是解答此类题目的关键.
12.【答案】
【解析】解:为锐角,且,
故答案为:
由特殊角的正切值,即可得到答案.
本题考查特殊角的三角函数值,关键是熟记特殊角的三角函数值.
13.【答案】
【解析】解:在中,,,,
,
,,
,,
,
故答案为:
首先在中利用勾股定理求出AB,再根据同角的余角相等得出,进而利用锐角三角函数关系即可求出的值.
此题主要考查了锐角三角函数关系的定义,得出是解题关键.
14.【答案】
【解析】解:斜坡AB的坡度:,
,
,
,
故答案为:
根据坡度的概念求出,再根据正弦的定义计算即可.
本题考查的是解直角三角形的应用-坡度坡角问题,熟记坡度是坡面的铅直高度h和水平宽度l的比是解题的关键.
15.【答案】
【解析】解:,
,,
,,
,,
,
故答案为:
根据绝对值和偶次方的非负性可得,,从而可得,,然后利用特殊角的三角函数值可得,,最后利用三角形内角和定理进行计算即可解答.
本题考查了特殊角的三角函数值,绝对值和偶次方的非负性,熟练掌握特殊角的三角函数值是解题的关键.
16.【答案】
【解析】略
17.【答案】解:原式
;
原式
【解析】先根据负整数指数幂,特殊角的三角函数值,二次根式的性质,零指数幂进行计算,再算加减即可;
先算括号内的加法,再把除法变成乘法,最后算乘法即可.
本题考查了零指数幂,负整数指数幂,实数的混合运算,特殊角的三角函数值,分式的混合运算等知识点,能正确运用实数和分式的运算法则进行计算是解此题的关键,注意运算顺序.
18.【答案】60 45
【解析】解:如图:
由题意得:,,,
,
,
由题意得:,
,
故答案为:60;45;
过点B作,垂足为G,
在中,,,
,
渔船航行时,距离小岛B最近;
如图:
在中,,,
,,
由题意得:,
在中,,
,
,
,
,
救援队从B处出发沿着南偏东方向航行到达事故地点航程最短,最短航程约为
根据题意可得:,,,从而可得,进而可得,然后再根据题意可得:,从而利用角的和差关系可得,即可解答;
过点B作,垂足为G,在中,利用锐角三角函数的定义求出AG的长,即可解答;
先在中,求出BG的长和的度数,再根据题意可得:,从而在中,利用锐角三角函数的定义求出,然后根据特殊角的三角函数值可得,再利用锐角三角函数的定义求出BC的长,最后利用平角定义求出的度数,即可解答.
本题考查了解直角三角形的应用-方向角问题,根据题目的已知条件并结合图形添加适当的辅助线是解题的关键.
19.【答案】解:延长AE,CD交于点G,连接AC,过点C作于点F,如图,
由题意得:米,米,,
景点C在景点A的东北方向,
在中,
,
,
米,米
,,
米,
米,
,,
米,
米,
,
,
米,
米,
米
答:景点A与景点E的距离359米.
乙先到达景点C,理由:
由知:米,
米,
甲到达点C所有的时间为分,
乙到达点C所有的时间为分,
,
乙先到达景点
【解析】延长AE,CD交于点G,连接AC,过点C作于点F,利用含角的直角三角形的性质,等腰直角三角形的性质解答即可;
利用的结论分别计算出甲,乙两人的走的路程,再计算出到达点C的时间即可.
本题主要考查了直角三角形的应用,含角的直角三角形的性质,等腰直角三角形的性质,勾股定理,方向角,近似数和有效数字,恰当的构造直角三角形是解题的关键.
20.【答案】解:能,理由如下:
延长EF交CH于N,如图所示:
则,
,
,
设,则,
,
在中,,
,
,
解得:,
,
答:点D到地面的距离DH的长约为
【解析】延长EF交CH于N,根据等腰直角三角形的性质得到,根据正切的定义求出DN,结合图形计算即可.
本题考查了解直角三角形的应用-仰角俯角问题,掌握仰角俯角的概念、熟记锐角三角函数的定义是解题的关键.
21.【答案】解:由题意得,,,
过点B作于点D,
,
,
,
千米,
在中,,
解得,
,
千米,
千米.
答:A、C两地的距离为千米.
【解析】由题意得,,则
过点B作于点D,在中,可得千米,千米,在中,可得千米,根据可得答案.
本题考查解直角三角形的应用-方向角问题,熟练掌握锐角三角函数的定义是解答本题的关键.
22.【答案】【小题1】
由题意,得,,
,
行进路线BC和CA所在直线的夹角的度数为
【小题2】
如图,过点A作,垂足为
在中,,,
,
在中,,
检查点B,C之间的距离为
【解析】见答案
见答案
23.【答案】解:由题意得:
,,,
设,
,
在中,,
,
在中,,
,
,
解得,
,
凉亭AB的高约为
【解析】本题考查了解直角三角形的应用-仰角俯角问题,熟练掌握锐角三角函数的定义是解题的关键.根据题意可得,,,然后设,则,在和中,利用锐角三角函数的定义分别求出AC的长,从而列出关于x的方程,进行计算即可解答.
24.【答案】解:过点B作于点则四边形AMEB是矩形.
,米,
,
在中,,
,
,
米,
在中,,,
,
,
米,
米
答:河流的宽度CD约为64米.
【解析】过点B作于点E,分别解、即可.
本题考查了关于俯仰角的解直角三角形的问题,作垂线构造直角三角形是解答本题的关键.
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第1章 图形的相似
- 1.1 相似多边形
- 1.2 怎样判定三角形相似
- 1.3 相似三角形的性质
- 1.4 图形的位似
- 第2章 解直角三角形
- 2.1 锐角三角比
- 2.2 30°,45°,60°角的三角比
- 2.3 用计算器求锐角三角比
- 2.4 解直角三角形
- 2.5 解直角三角形的应用
- 第3章 对圆的进一步认识
- 3.1 圆的对称性
- 3.2 确定圆的条件
- 3.3 圆周角
- 3.4 直线与圆的位置关系
- 3.5 三角形的内切圆
- 3.6 弧长及扇形面积的计算
- 3.7 正多边形与圆
- 课题学习 图形变换与图案设计
- 第4章 一元二次方程
- 4.1 一元二次方程
- 4.2 用配方法解一元二次方程
- 4.3 用公式法解一元二次方程
- 4.4 用因式分解法解一元二次方程
- 4.5 一元二次方程的应用
- 4.6 一元二次方程根与系数的关系
