29.2三视图 (44张PPT)
文档属性
| 名称 | 29.2三视图 (44张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 6.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-01-11 00:00:00 | ||
图片预览





文档简介
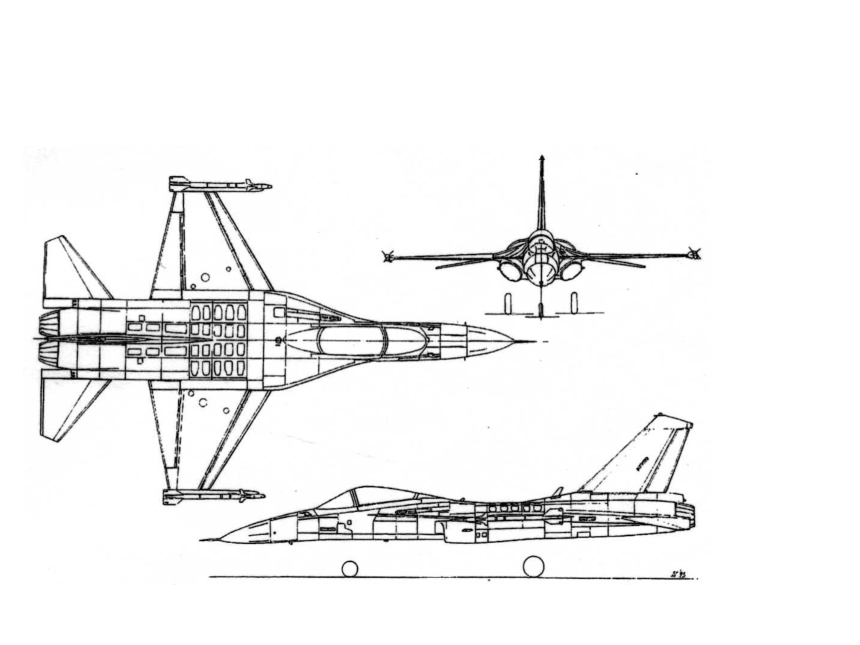
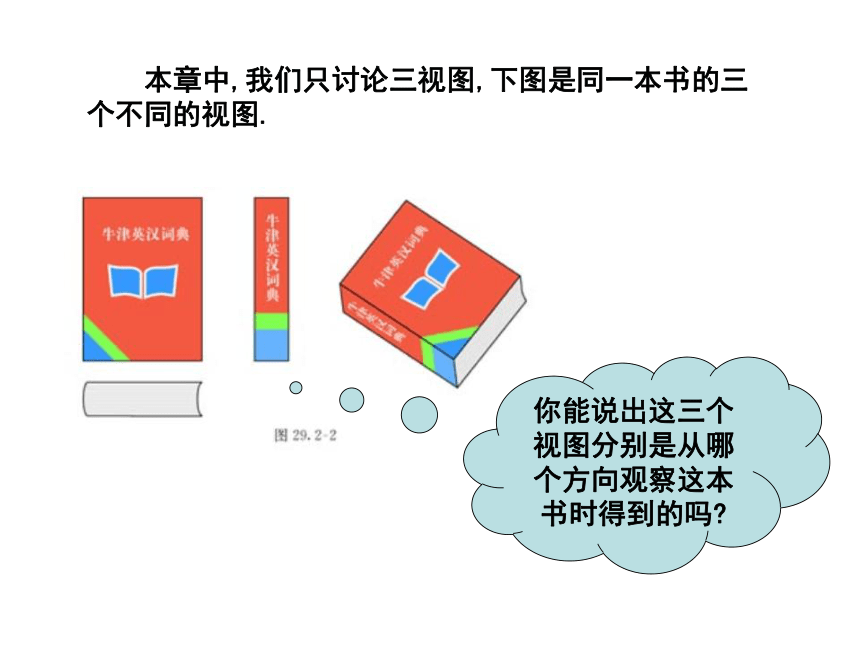
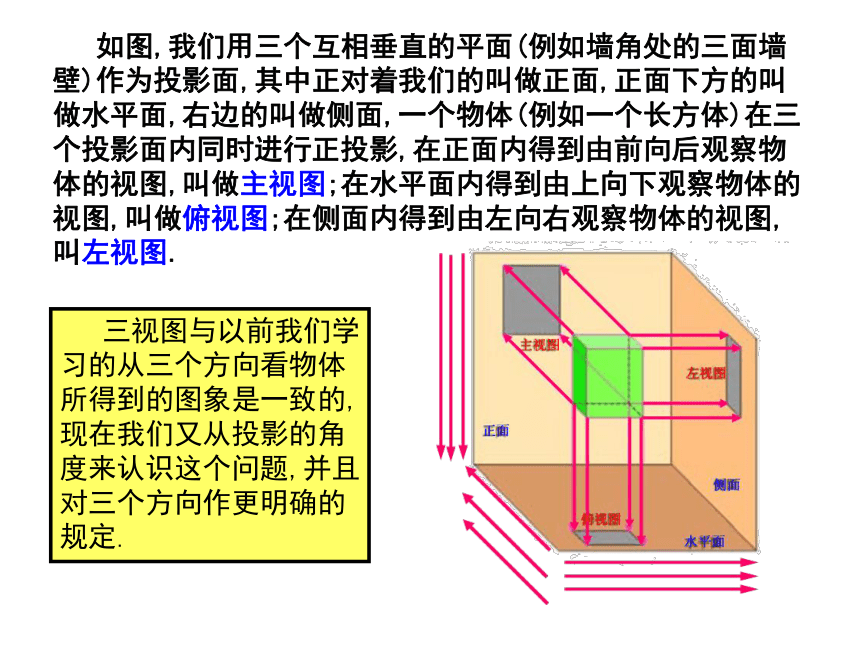
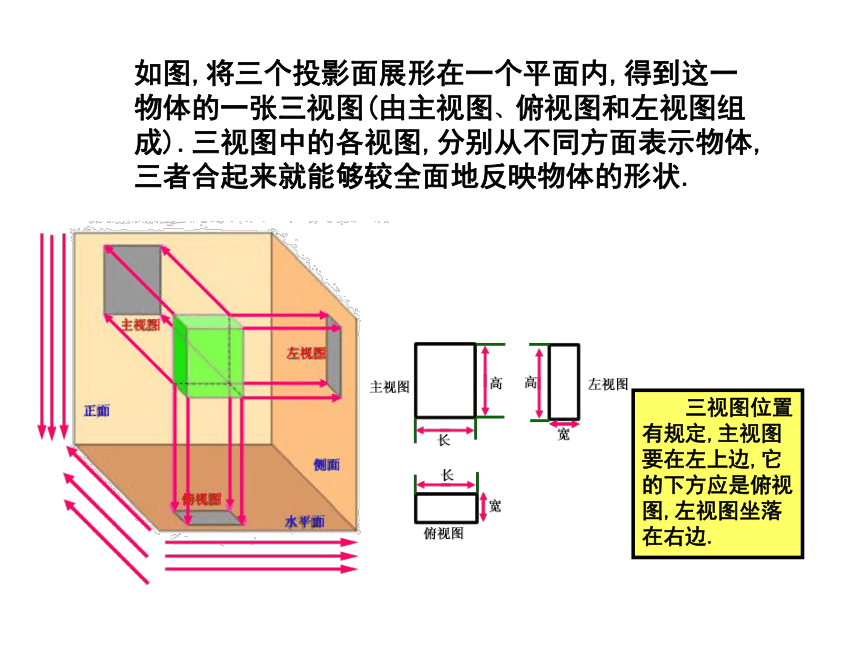
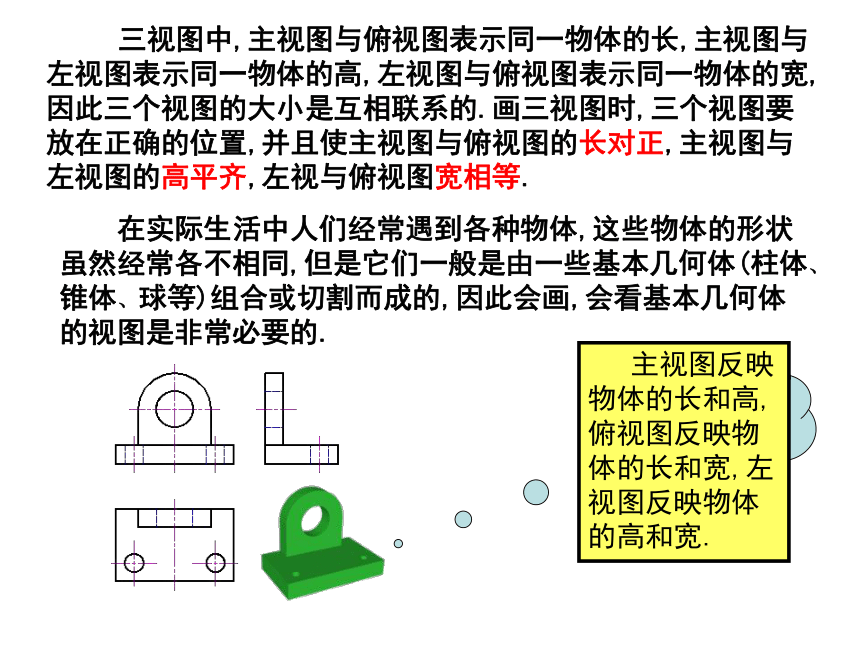
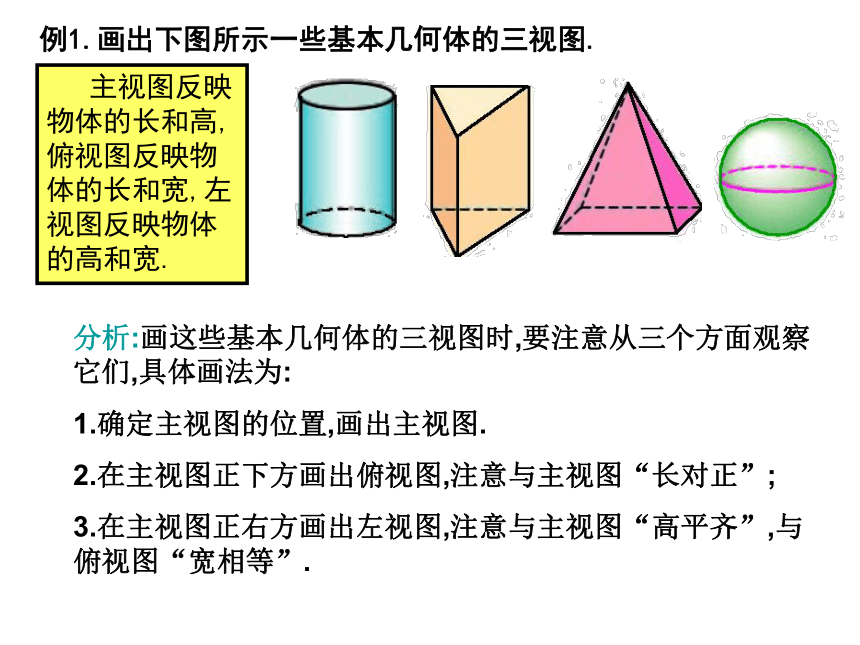
课件44张PPT。29.2三视图 从我们从某一角度观察一个物体时,所看到图象叫做物体的一个视图(vicw).视图也可以看作物体在某一角度的光线下的投影,对于同一物体,如果从不同角度观察,所得到的视图可能不同. 我们知道,单一的视图通常只能反映物体的一个方面的形状,为了全面地反映物体的形状,生产实践中往往采用多个视图来反映物体不同方面的形状.例如图中右侧的视图,可以多角度地反映飞机的形状. 本章中,我们只讨论三视图,下图是同一本书的三个不同的视图.你能说出这三个视图分别是从哪个方向观察这本书时得到的吗? 三视图与以前我们学习的从三个方向看物体所得到的图象是一致的,现在我们又从投影的角度来认识这个问题,并且对三个方向作更明确的规定. 如图,我们用三个互相垂直的平面(例如墙角处的三面墙壁)作为投影面,其中正对着我们的叫做正面,正面下方的叫做水平面,右边的叫做侧面,一个物体(例如一个长方体)在三个投影面内同时进行正投影,在正面内得到由前向后观察物体的视图,叫做主视图;在水平面内得到由上向下观察物体的视图,叫做俯视图;在侧面内得到由左向右观察物体的视图,叫左视图.如图,将三个投影面展形在一个平面内,得到这一物体的一张三视图(由主视图、俯视图和左视图组成).三视图中的各视图,分别从不同方面表示物体,三者合起来就能够较全面地反映物体的形状. 三视图位置有规定,主视图要在左上边,它的下方应是俯视图,左视图坐落在右边.三视图中各视图的大小有什么关系? 三视图中,主视图与俯视图表示同一物体的长,主视图与左视图表示同一物体的高,左视图与俯视图表示同一物体的宽,因此三个视图的大小是互相联系的.画三视图时,三个视图要放在正确的位置,并且使主视图与俯视图的长对正,主视图与左视图的高平齐,左视与俯视图宽相等. 在实际生活中人们经常遇到各种物体,这些物体的形状虽然经常各不相同,但是它们一般是由一些基本几何体(柱体、锥体、球等)组合或切割而成的,因此会画,会看基本几何体的视图是非常必要的. 主视图反映物体的长和高,俯视图反映物体的长和宽,左视图反映物体的高和宽.例1.画出下图所示一些基本几何体的三视图. 主视图反映物体的长和高,俯视图反映物体的长和宽,左视图反映物体的高和宽.分析:画这些基本几何体的三视图时,要注意从三个方面观察它们,具体画法为:
1.确定主视图的位置,画出主视图.
2.在主视图正下方画出俯视图,注意与主视图“长对正”;
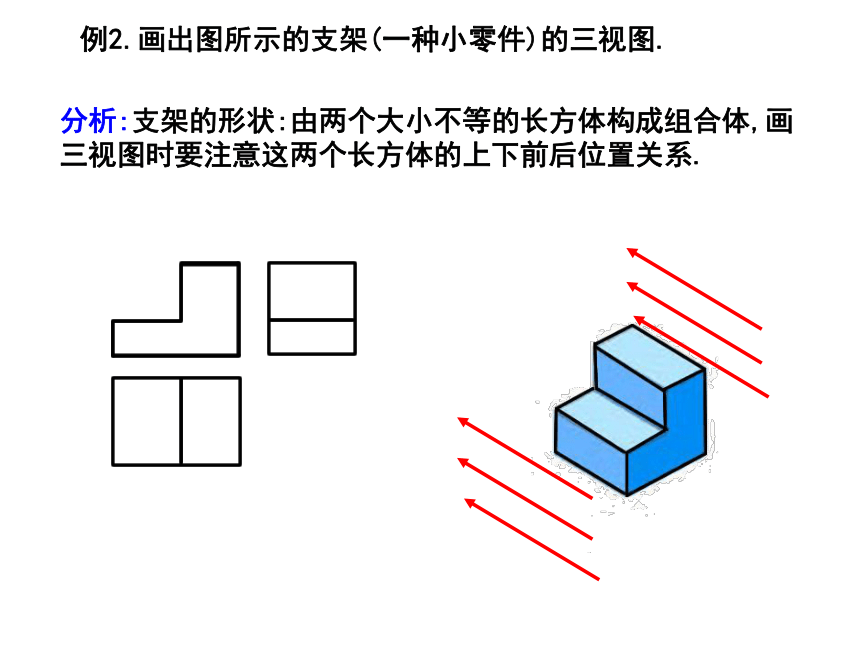
3.在主视图正右方画出左视图,注意与主视图“高平齐”,与俯视图“宽相等”.例2.画出图所示的支架(一种小零件)的三视图.分析:支架的形状:由两个大小不等的长方体构成组合体,画三视图时要注意这两个长方体的上下前后位置关系.例3.下图是一根钢管直观图,画出它的三视图.分析:钢管有内外壁,从一定角度看它时,看不见内壁,为全面地反映立体图形的形状,画图时规定:看得见部分的轮廊画成实线,因被其他部分遮挡面看不见部分的轮廓线画成虚线.解:右图为钢管的三视图,其中虚线表示钢管的内壁.1.画出如图所示的三棱柱的三视图(这个三棱柱上下底是正三角形).练习2.画出半球和圆锥的三视图.2.画出半球和圆锥的三视图.3.图中的立体图形可以看成由哪些基本几何体经过怎样的变化得到的?画出它的三视图. 前面我们讨论了由立体图形(实物)画出三视图,下面我们讨论由三视图想象出的立体图形(实物).分析:由三视图想象立体图形时,要先分别根据主视图、俯视图和左视图想象立体图形的前面上面和左侧面,然后再综合起来考虑整体图形. 前面我们讨论了由立体图形(实物)画出三视图,下面我们讨论由三视图想象出的立体图形(实物).解:(1)从三个方向看立体图形,图象都是矩形,可以想象出:整体是长方体.(2)从正面、侧面看立体图形,图象都是等腰三角形;从上面看,图角是图;可以想象出:整体是圆锥.例5根据物体的三视图,描述物体的形状.请对照在三视图与想象出的立体图形,指出三视图中各线条分别是立体图形哪部分的投影. 分析:由主视图可知,物体正面是画正五边形;由俯视图可知,由上向下看物体是矩形的,且有一条棱(中间的实线)可见到,两条棱(虚线)被遮挡;由左视图可知,物体的侧面是矩形的,且有一条棱(中间实线)可见到,综合各视图可知,物体是五棱柱形.解:物体是五棱柱形状的.练习由三视图想象实物形状;练习由三视图想象实物形状;例6 某工厂要加工一密罐,设计者给出了密封罐的三视图,请你按照三视图确定制作每个密封罐所需钢板的面积.分析:对于某些立体图形,沿着其中一些线(例如棱柱的棱)剪开,可以把立体图形的表面展开成一个平面图形----展形图,在实际的生产中,三视图和展开图往往结合在一起使用,解决本题的思路是:三视图想象出密封罐的立体形状,再进一步画出展开图,从而计算面积.解:由展开图可知,制作一个密封罐所需钢板的面积为:练习根据几何体的三视图画出它的表面展开图:请您欣赏再见
1.确定主视图的位置,画出主视图.
2.在主视图正下方画出俯视图,注意与主视图“长对正”;
3.在主视图正右方画出左视图,注意与主视图“高平齐”,与俯视图“宽相等”.例2.画出图所示的支架(一种小零件)的三视图.分析:支架的形状:由两个大小不等的长方体构成组合体,画三视图时要注意这两个长方体的上下前后位置关系.例3.下图是一根钢管直观图,画出它的三视图.分析:钢管有内外壁,从一定角度看它时,看不见内壁,为全面地反映立体图形的形状,画图时规定:看得见部分的轮廊画成实线,因被其他部分遮挡面看不见部分的轮廓线画成虚线.解:右图为钢管的三视图,其中虚线表示钢管的内壁.1.画出如图所示的三棱柱的三视图(这个三棱柱上下底是正三角形).练习2.画出半球和圆锥的三视图.2.画出半球和圆锥的三视图.3.图中的立体图形可以看成由哪些基本几何体经过怎样的变化得到的?画出它的三视图. 前面我们讨论了由立体图形(实物)画出三视图,下面我们讨论由三视图想象出的立体图形(实物).分析:由三视图想象立体图形时,要先分别根据主视图、俯视图和左视图想象立体图形的前面上面和左侧面,然后再综合起来考虑整体图形. 前面我们讨论了由立体图形(实物)画出三视图,下面我们讨论由三视图想象出的立体图形(实物).解:(1)从三个方向看立体图形,图象都是矩形,可以想象出:整体是长方体.(2)从正面、侧面看立体图形,图象都是等腰三角形;从上面看,图角是图;可以想象出:整体是圆锥.例5根据物体的三视图,描述物体的形状.请对照在三视图与想象出的立体图形,指出三视图中各线条分别是立体图形哪部分的投影. 分析:由主视图可知,物体正面是画正五边形;由俯视图可知,由上向下看物体是矩形的,且有一条棱(中间的实线)可见到,两条棱(虚线)被遮挡;由左视图可知,物体的侧面是矩形的,且有一条棱(中间实线)可见到,综合各视图可知,物体是五棱柱形.解:物体是五棱柱形状的.练习由三视图想象实物形状;练习由三视图想象实物形状;例6 某工厂要加工一密罐,设计者给出了密封罐的三视图,请你按照三视图确定制作每个密封罐所需钢板的面积.分析:对于某些立体图形,沿着其中一些线(例如棱柱的棱)剪开,可以把立体图形的表面展开成一个平面图形----展形图,在实际的生产中,三视图和展开图往往结合在一起使用,解决本题的思路是:三视图想象出密封罐的立体形状,再进一步画出展开图,从而计算面积.解:由展开图可知,制作一个密封罐所需钢板的面积为:练习根据几何体的三视图画出它的表面展开图:请您欣赏再见
