上海市各区县2016届高三上学期期末考试数学理试题汇编:函数
文档属性
| 名称 | 上海市各区县2016届高三上学期期末考试数学理试题汇编:函数 |  | |
| 格式 | zip | ||
| 文件大小 | 329.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-01-11 15:31:01 | ||
图片预览



文档简介
上海市各区县2016届高三上学期期末考试数学理试题汇编
函数
一、填空题
1、(宝山区2016届高三上学期期末)方程的解集为 .
2、(崇明县2016届高三上学期期末)已 ( http: / / www.21cnjy.com )知 f (x)、g(x)分别是定义在R上的偶函数和奇函数,且 f (x) g(x) =2x+x,则f (1) +g(1) =
3、(奉贤区2016届高三上学期期末)方程的实数解为_________
4、(虹口区2016届高三上学期期末)函数的反函数
5、(黄浦区2016届高三上学期期末)若函数为偶函数且非奇函数,则实数的取值范围为 .
6、(金山区2016届高三上学期期末)方程4x– 62x +8=0的解是
7、(静安区2016届高三上学期期末)方程的解为 .
8、(闵行区2016届高三上学期期末)方程的解为 .
9、(普陀区2016届高三上学期期末)若函数,,则________.
10、(青浦区2016届高三上学期期末)函数,若,则实数的取值范围是 .
11、(松江区2016届高三上学期期末)若幂函数的图像过点,则= ▲ .
12、(杨浦区2016届高三上学期期末)已知函数 ,则方程的解 = _____________.
13、(闸北区2016届高三上学期期末)函数的单调性为 ;奇偶性为 ;
14、(长宁区2016届高三上学期期末)方程9x +3x -2 = 0的解是___________.
15、(闵行区2016届高三上学期期末)若函数满足,且在上单调递增,则实数的最小值等于 .
16、(青浦区2016届高三上学期期末)函数的定义域为 .
17、(松江区2016届高三上学期期末)已知函数,对任意的,恒有成立, 且当时,. 则方程在区间上所有根的和为 ▲ .
18、(杨浦区2016届高三上学期期末)已知是定义在上的奇函数,当时,,当时,,若直线与函数的图象恰有11个不同的公共点,则实数的取值范围为____________.
19、(长宁区2016届高三上学期期末)设函数 y =f(x)的反函数是 y =f-1(x),且函数 y=f(x)过点P(2,-1),则
f-1(-1)= ___________.
二、选择题
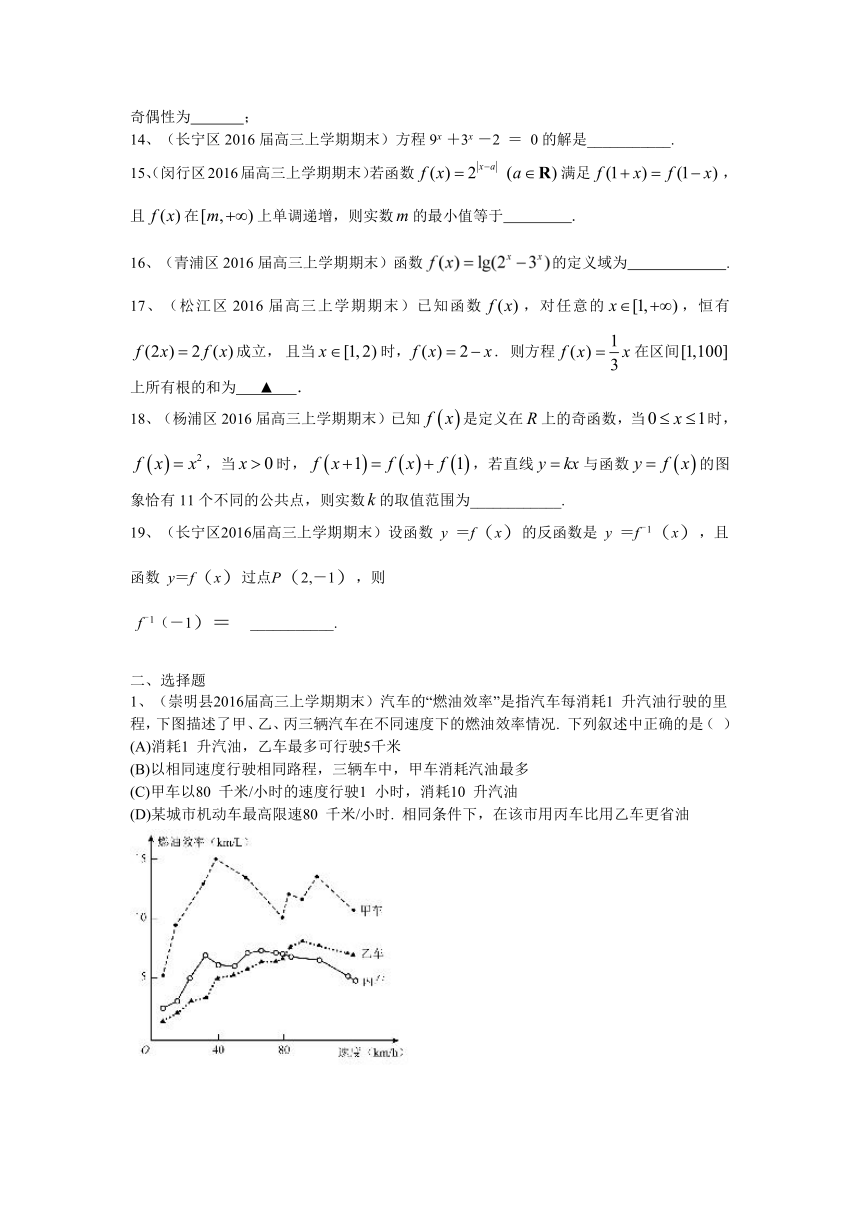
1、(崇明县2016届高三上学期期末)汽车 ( http: / / www.21cnjy.com )的“燃油效率”是指汽车每消耗1 升汽油行驶的里程,下图描述了甲、乙、丙三辆汽车在不同速度下的燃油效率情况. 下列叙述中正确的是( )
(A)消耗1 升汽油,乙车最多可行驶5千米
(B)以相同速度行驶相同路程,三辆车中,甲车消耗汽油最多
(C)甲车以80 千米/小时的速度行驶1 小时,消耗10 升汽油
(D)某城市机动车最高限速80 千米/小时. 相同条件下,在该市用丙车比用乙车更省油
( http: / / www.21cnjy.com )
2、(虹口区2016届高三上学期期末)设函数 若关于的方程有四个不同的解
且则的取值范围是 ( )
(A) (B) (C) (D)
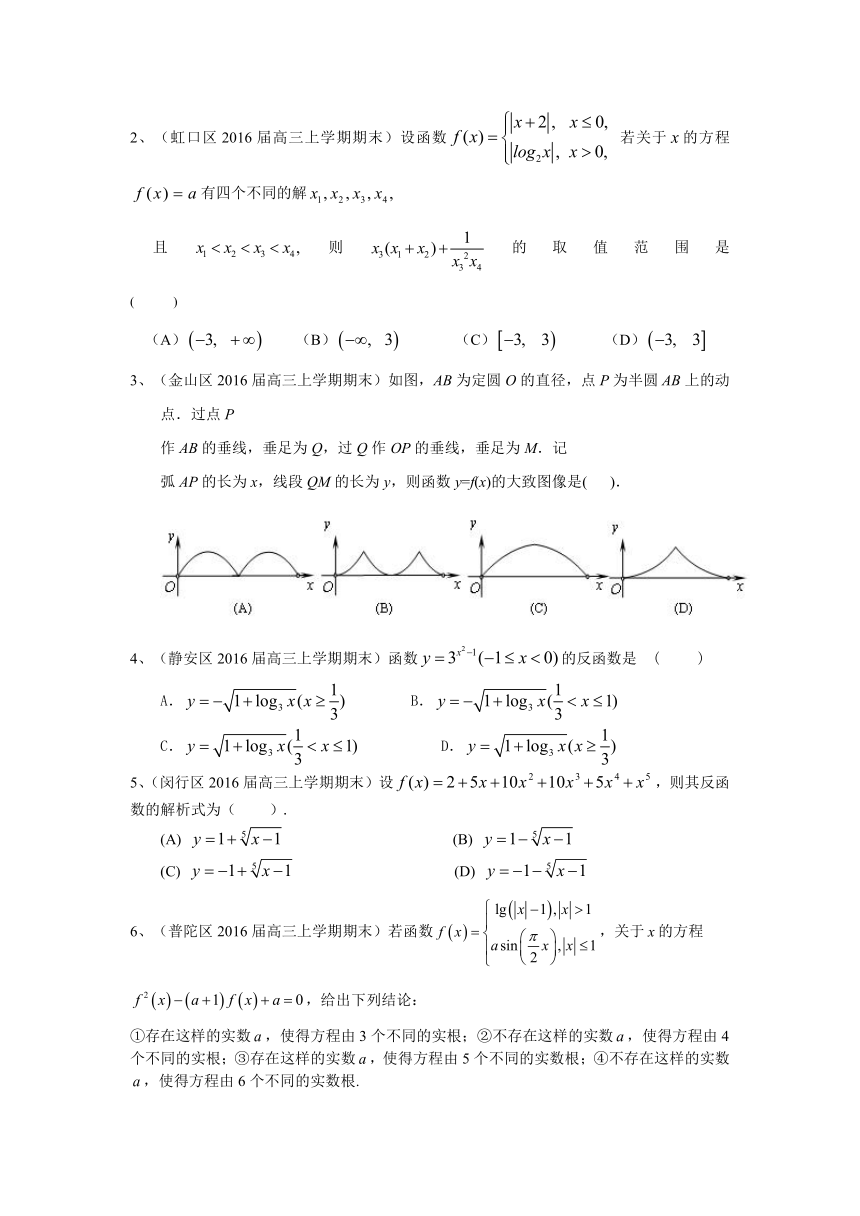
3、(金山区2016届高三上学期期末)如图,AB为定圆O的直径,点P为半圆AB上的动点.过点P
作AB的垂线,垂足为Q,过Q作OP的垂线,垂足为M.记
弧AP的长为x,线段QM的长为y,则函数y=f(x)的大致图像是( ).
( http: / / www.21cnjy.com )
4、(静安区2016届高三上学期期末)函数的反函数是 ( )
A. B.
C. D.
5、(闵行区2016届高三上学期期末)设,则其反函数的解析式为( ).
(A) (B)
(C) (D)
6、(普陀区2016届高三上学期期末)若函数,关于的方程
,给出下列结论:
①存在这样的实数,使得方程由3个不同的实根;②不存在这样的实数,使得方程由4个不同的实根;③存在这样的实数,使得方程由5个不同的实数根;④不存在这样的实数,使得方程由6个不同的实数根.
其中正确的个数是( )
1个 2个 3个 4个
7、(杨浦区2016届高三上学期期末)下列函数中,既是偶函数,又在 上递增的函数的个数是 ( )
① ② ③ ④
A. 1个 B. 2个 C. 3个 D. 4个
8、(长宁区2016届高三上学期期末)关于函数,有下列四个命题:①的值域是;
② 是奇函数;③ 在上单调递增;④方程总有四个不同的解.其中正确的是 ( )
A. ①② B. ②③ C. ②④ D. ③④
三、解答题
1、(奉贤区2016届高三上学期期末)已知函数是单调递增函数,其反函数是.
(1)、若,求并写出定义域;
(2)、对于(1)的和,设任意,
求证:;
(3)、若和有交点,那么交点一定在上.
2、(虹口区2016届高三上学期期末)
对于函数定义已知偶函数的定义域为
(1)求并求出函数的解析式;
(2) 若存在实数使得函数上的值域为,求实数的取值范围.
3、(静安区2016届高三上学期期末)已知定义在实数集R上的偶函数和奇函数满足.
(1)求与的解析式;
(2)若定义在实数集R上的以2为最小正周期的周期函数,当时,,试求在闭区间上的表达式,并证明在闭区间上单调递减;
(3)设(其中m为常数),若对于恒成立,求m的取值范围.
4、(普陀区2016届高三上学期期末)已知集合是满足下列性质的函数的全体,存在实数,对于定义域内的任意均有成立,称数对为函数的“伴随数对”
(1)判断是否属于集合,并说明理由;
(2)若函数,求满足条件的函数的所有“伴随数对”;
(3)若都是函数的“伴随数对”,当时,;
当时,.求当时,函数的解析式和零点.
5、(杨浦区2016届高三上学期期末)已知函数,若存在常数T(T>0),对任意都有,则称函数为T倍周期函数
(1)判断是否是T倍周期函数,并说明理由.
(2)证明是T倍周期函数,且T的值是唯一的.
(3)若是2倍周期函数,,, 表示的前n 项和,,若恒成立,求a的取值范围.
6、(长宁区2016届高三上学期期末)已知函数,如果对于定义域D内的任意实数x,对于给定的非零常数m ,总存在非零常数T ,恒有成立,则称函数是D上的m 级类增周期函数,周期为T .若恒有成立,则称函数 是D上的m 级类周期函数,周期为T .
(1)已知函数上的周期为 1 的 2 级类增周期函数,求实数a的取值范围;
(2)已知上的m 级类周期函数,且上的单调递增函数,当时,,求实数m 的取值范围.
参考答案
一、填空题
1、 2、- 3、 4、 5、
6、x=1或x=2 7、 8、 9、 10、
11、 12、1 13、单调递增,奇函数 14、x=0 15、1
16、 17、 18、(,) 19、2
二、选择题
1、D 2、D 3、A 4、B 5、C 6、C 7、A 8、B
三、解答题
1、解:(1)、 3+2=5分
(2)、 7分
, 9分
, 10分
11分
(3)、设是和有交点
即, 12分
当,显然在上 13分
当,函数是单调递增函数,矛盾 15分
当,函数是单调递增函数,矛盾 16分
因此,若和的交点一定在上 16分
2、解:(1)因为
故对任意的
于是
由为偶函数,
. ……(6分)
(2) 由于的定义域为,
又
且 ……(8分)
函数的图像,如图所示. 由题意,有
……(10分)
故是方程的两个不相等的负实数根,即方程在上有
两个不相等的实根,于是
……(12分)
综合上述,得:实数的取值范围为 ……(14分)
注:若采用数形结合,得出直线与曲线有两个不同交点,并进行求解也可.
3、解:(1)假设①,因为是偶函数, 是奇函数
所以有,即 ②
∵,定义在实数集R上,
由①和②解得,
,.
(2) 是R上以2为正周期的周期函数, 所以当时, ,,即在闭区间上的表达式为.
下面证明在闭区间上递减:
,当且仅当,即时等号成立.对于任意,,
因为,所以,,,,,
从而,所以当时, 递减.
(证明在上递减,再根据周期性或者复合函数单调性得到也可)
(3)∵在单调递增,∴.
∴对于恒成立,
∴对于恒成立,
令,则,当且仅当时,等号成立,且所以在区间上单调递减,
∴,∴为m的取值范围.
4、
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
5、(1) 设:
则 对任意x恒成立 (2分)
无解
不是T倍周期函数 (2分)
(2) 设:
则 对任意x恒成立 (2分)
(2分)
下证唯一性:
若, 矛盾
若, 矛盾
是唯一的 (2分)
(3)
(2分)
同理:
同理:
(2分)
显然: 且
即单调递减
(2分)
恒成立,
① 时 解得 :
② 时 解得 :
或 (2分)
6、1)由题意可知:f(x+1)>2f(x),即-(x+1)2+a(x+1)>2(-x2+ax)对一切[3,+∞)恒成立,
整理得:(x-1)a<x2-2x-1,
∵x≥3,
令x-1=t,则t∈[2,+∞),g(t)=t-
在[2,+∞)上单调递增,
∴g(t)mi ( http: / / www.21cnjy.com )n=g(2)=1,
∴a<1.
(2)∵x∈[0,1)时,f(x)=2x,
∴当x∈[1,2)时,f(x)=mf(x-1)=m 2x-1,…
当x∈[n,n+1)时,f(x)=mf(x-1)=m2f(x-2)=…=mnf(x-n)=mn 2x-n,
即x∈[n,n+1)时,f(x)=mn 2x-n,n∈N*,
∵f(x)在[0,+∞)上单调递增,
∴m>0且mn 2n-n≥mn-1 2n-(n-1),
即m≥2.
函数
一、填空题
1、(宝山区2016届高三上学期期末)方程的解集为 .
2、(崇明县2016届高三上学期期末)已 ( http: / / www.21cnjy.com )知 f (x)、g(x)分别是定义在R上的偶函数和奇函数,且 f (x) g(x) =2x+x,则f (1) +g(1) =
3、(奉贤区2016届高三上学期期末)方程的实数解为_________
4、(虹口区2016届高三上学期期末)函数的反函数
5、(黄浦区2016届高三上学期期末)若函数为偶函数且非奇函数,则实数的取值范围为 .
6、(金山区2016届高三上学期期末)方程4x– 62x +8=0的解是
7、(静安区2016届高三上学期期末)方程的解为 .
8、(闵行区2016届高三上学期期末)方程的解为 .
9、(普陀区2016届高三上学期期末)若函数,,则________.
10、(青浦区2016届高三上学期期末)函数,若,则实数的取值范围是 .
11、(松江区2016届高三上学期期末)若幂函数的图像过点,则= ▲ .
12、(杨浦区2016届高三上学期期末)已知函数 ,则方程的解 = _____________.
13、(闸北区2016届高三上学期期末)函数的单调性为 ;奇偶性为 ;
14、(长宁区2016届高三上学期期末)方程9x +3x -2 = 0的解是___________.
15、(闵行区2016届高三上学期期末)若函数满足,且在上单调递增,则实数的最小值等于 .
16、(青浦区2016届高三上学期期末)函数的定义域为 .
17、(松江区2016届高三上学期期末)已知函数,对任意的,恒有成立, 且当时,. 则方程在区间上所有根的和为 ▲ .
18、(杨浦区2016届高三上学期期末)已知是定义在上的奇函数,当时,,当时,,若直线与函数的图象恰有11个不同的公共点,则实数的取值范围为____________.
19、(长宁区2016届高三上学期期末)设函数 y =f(x)的反函数是 y =f-1(x),且函数 y=f(x)过点P(2,-1),则
f-1(-1)= ___________.
二、选择题
1、(崇明县2016届高三上学期期末)汽车 ( http: / / www.21cnjy.com )的“燃油效率”是指汽车每消耗1 升汽油行驶的里程,下图描述了甲、乙、丙三辆汽车在不同速度下的燃油效率情况. 下列叙述中正确的是( )
(A)消耗1 升汽油,乙车最多可行驶5千米
(B)以相同速度行驶相同路程,三辆车中,甲车消耗汽油最多
(C)甲车以80 千米/小时的速度行驶1 小时,消耗10 升汽油
(D)某城市机动车最高限速80 千米/小时. 相同条件下,在该市用丙车比用乙车更省油
( http: / / www.21cnjy.com )
2、(虹口区2016届高三上学期期末)设函数 若关于的方程有四个不同的解
且则的取值范围是 ( )
(A) (B) (C) (D)
3、(金山区2016届高三上学期期末)如图,AB为定圆O的直径,点P为半圆AB上的动点.过点P
作AB的垂线,垂足为Q,过Q作OP的垂线,垂足为M.记
弧AP的长为x,线段QM的长为y,则函数y=f(x)的大致图像是( ).
( http: / / www.21cnjy.com )
4、(静安区2016届高三上学期期末)函数的反函数是 ( )
A. B.
C. D.
5、(闵行区2016届高三上学期期末)设,则其反函数的解析式为( ).
(A) (B)
(C) (D)
6、(普陀区2016届高三上学期期末)若函数,关于的方程
,给出下列结论:
①存在这样的实数,使得方程由3个不同的实根;②不存在这样的实数,使得方程由4个不同的实根;③存在这样的实数,使得方程由5个不同的实数根;④不存在这样的实数,使得方程由6个不同的实数根.
其中正确的个数是( )
1个 2个 3个 4个
7、(杨浦区2016届高三上学期期末)下列函数中,既是偶函数,又在 上递增的函数的个数是 ( )
① ② ③ ④
A. 1个 B. 2个 C. 3个 D. 4个
8、(长宁区2016届高三上学期期末)关于函数,有下列四个命题:①的值域是;
② 是奇函数;③ 在上单调递增;④方程总有四个不同的解.其中正确的是 ( )
A. ①② B. ②③ C. ②④ D. ③④
三、解答题
1、(奉贤区2016届高三上学期期末)已知函数是单调递增函数,其反函数是.
(1)、若,求并写出定义域;
(2)、对于(1)的和,设任意,
求证:;
(3)、若和有交点,那么交点一定在上.
2、(虹口区2016届高三上学期期末)
对于函数定义已知偶函数的定义域为
(1)求并求出函数的解析式;
(2) 若存在实数使得函数上的值域为,求实数的取值范围.
3、(静安区2016届高三上学期期末)已知定义在实数集R上的偶函数和奇函数满足.
(1)求与的解析式;
(2)若定义在实数集R上的以2为最小正周期的周期函数,当时,,试求在闭区间上的表达式,并证明在闭区间上单调递减;
(3)设(其中m为常数),若对于恒成立,求m的取值范围.
4、(普陀区2016届高三上学期期末)已知集合是满足下列性质的函数的全体,存在实数,对于定义域内的任意均有成立,称数对为函数的“伴随数对”
(1)判断是否属于集合,并说明理由;
(2)若函数,求满足条件的函数的所有“伴随数对”;
(3)若都是函数的“伴随数对”,当时,;
当时,.求当时,函数的解析式和零点.
5、(杨浦区2016届高三上学期期末)已知函数,若存在常数T(T>0),对任意都有,则称函数为T倍周期函数
(1)判断是否是T倍周期函数,并说明理由.
(2)证明是T倍周期函数,且T的值是唯一的.
(3)若是2倍周期函数,,, 表示的前n 项和,,若恒成立,求a的取值范围.
6、(长宁区2016届高三上学期期末)已知函数,如果对于定义域D内的任意实数x,对于给定的非零常数m ,总存在非零常数T ,恒有成立,则称函数是D上的m 级类增周期函数,周期为T .若恒有成立,则称函数 是D上的m 级类周期函数,周期为T .
(1)已知函数上的周期为 1 的 2 级类增周期函数,求实数a的取值范围;
(2)已知上的m 级类周期函数,且上的单调递增函数,当时,,求实数m 的取值范围.
参考答案
一、填空题
1、 2、- 3、 4、 5、
6、x=1或x=2 7、 8、 9、 10、
11、 12、1 13、单调递增,奇函数 14、x=0 15、1
16、 17、 18、(,) 19、2
二、选择题
1、D 2、D 3、A 4、B 5、C 6、C 7、A 8、B
三、解答题
1、解:(1)、 3+2=5分
(2)、 7分
, 9分
, 10分
11分
(3)、设是和有交点
即, 12分
当,显然在上 13分
当,函数是单调递增函数,矛盾 15分
当,函数是单调递增函数,矛盾 16分
因此,若和的交点一定在上 16分
2、解:(1)因为
故对任意的
于是
由为偶函数,
. ……(6分)
(2) 由于的定义域为,
又
且 ……(8分)
函数的图像,如图所示. 由题意,有
……(10分)
故是方程的两个不相等的负实数根,即方程在上有
两个不相等的实根,于是
……(12分)
综合上述,得:实数的取值范围为 ……(14分)
注:若采用数形结合,得出直线与曲线有两个不同交点,并进行求解也可.
3、解:(1)假设①,因为是偶函数, 是奇函数
所以有,即 ②
∵,定义在实数集R上,
由①和②解得,
,.
(2) 是R上以2为正周期的周期函数, 所以当时, ,,即在闭区间上的表达式为.
下面证明在闭区间上递减:
,当且仅当,即时等号成立.对于任意,,
因为,所以,,,,,
从而,所以当时, 递减.
(证明在上递减,再根据周期性或者复合函数单调性得到也可)
(3)∵在单调递增,∴.
∴对于恒成立,
∴对于恒成立,
令,则,当且仅当时,等号成立,且所以在区间上单调递减,
∴,∴为m的取值范围.
4、
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
5、(1) 设:
则 对任意x恒成立 (2分)
无解
不是T倍周期函数 (2分)
(2) 设:
则 对任意x恒成立 (2分)
(2分)
下证唯一性:
若, 矛盾
若, 矛盾
是唯一的 (2分)
(3)
(2分)
同理:
同理:
(2分)
显然: 且
即单调递减
(2分)
恒成立,
① 时 解得 :
② 时 解得 :
或 (2分)
6、1)由题意可知:f(x+1)>2f(x),即-(x+1)2+a(x+1)>2(-x2+ax)对一切[3,+∞)恒成立,
整理得:(x-1)a<x2-2x-1,
∵x≥3,
令x-1=t,则t∈[2,+∞),g(t)=t-
在[2,+∞)上单调递增,
∴g(t)mi ( http: / / www.21cnjy.com )n=g(2)=1,
∴a<1.
(2)∵x∈[0,1)时,f(x)=2x,
∴当x∈[1,2)时,f(x)=mf(x-1)=m 2x-1,…
当x∈[n,n+1)时,f(x)=mf(x-1)=m2f(x-2)=…=mnf(x-n)=mn 2x-n,
即x∈[n,n+1)时,f(x)=mn 2x-n,n∈N*,
∵f(x)在[0,+∞)上单调递增,
∴m>0且mn 2n-n≥mn-1 2n-(n-1),
即m≥2.
同课章节目录
