作轴对称图形
图片预览





文档简介
课件43张PPT。对称是一种思想,通过它,人们毕生追求,
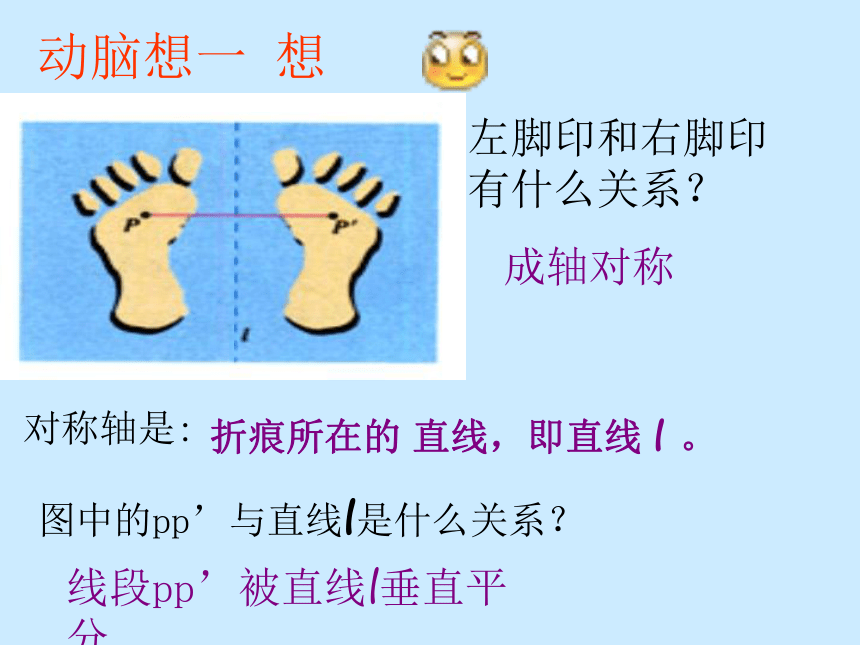
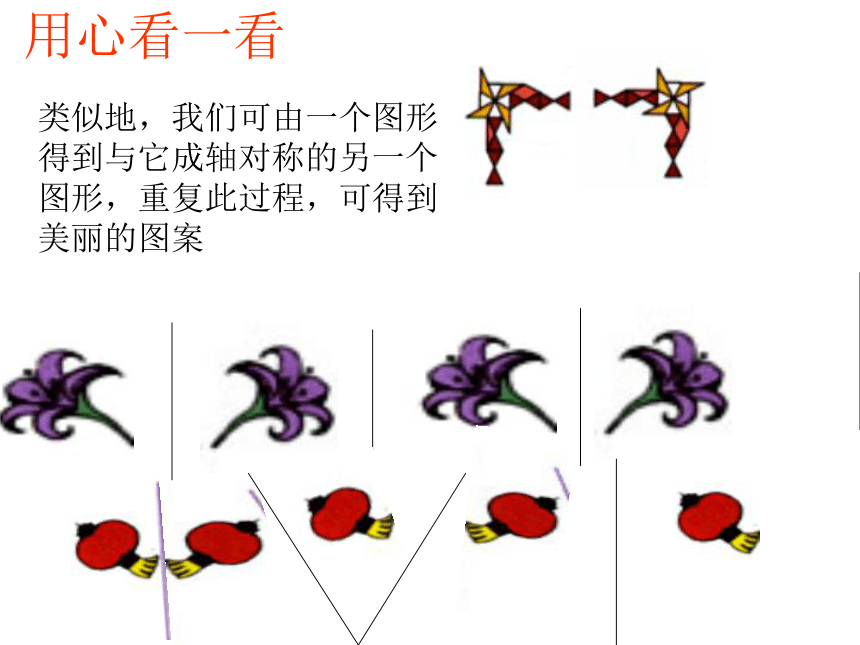
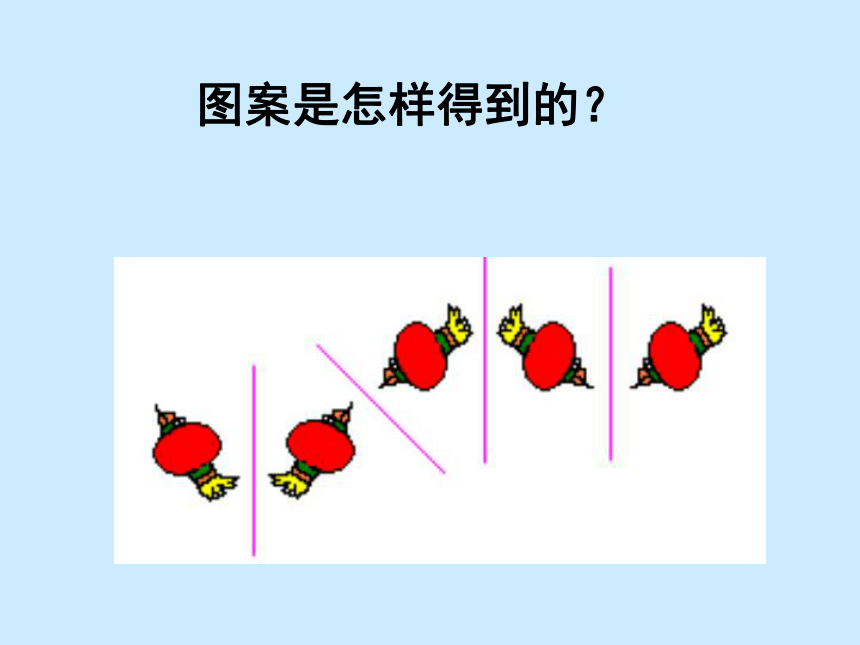
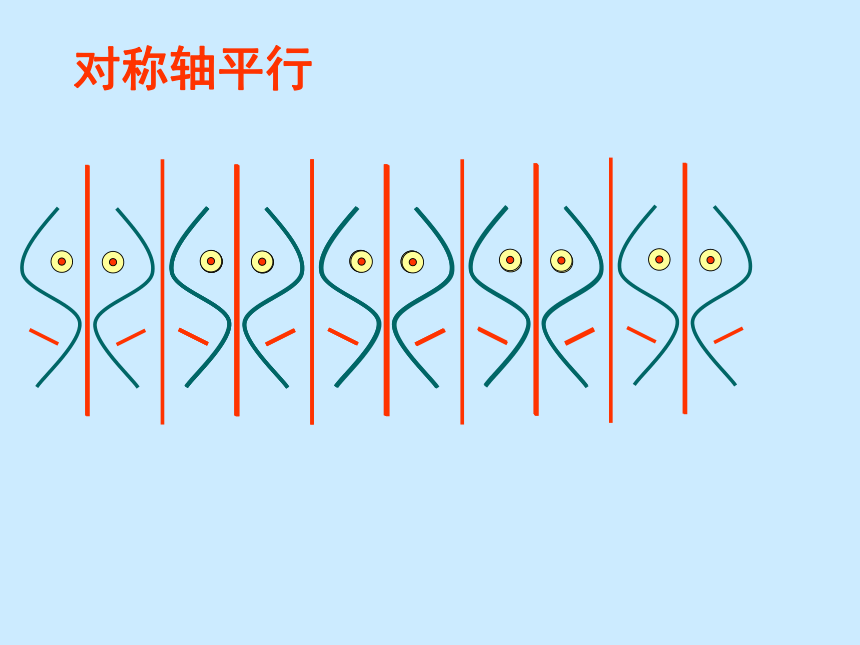
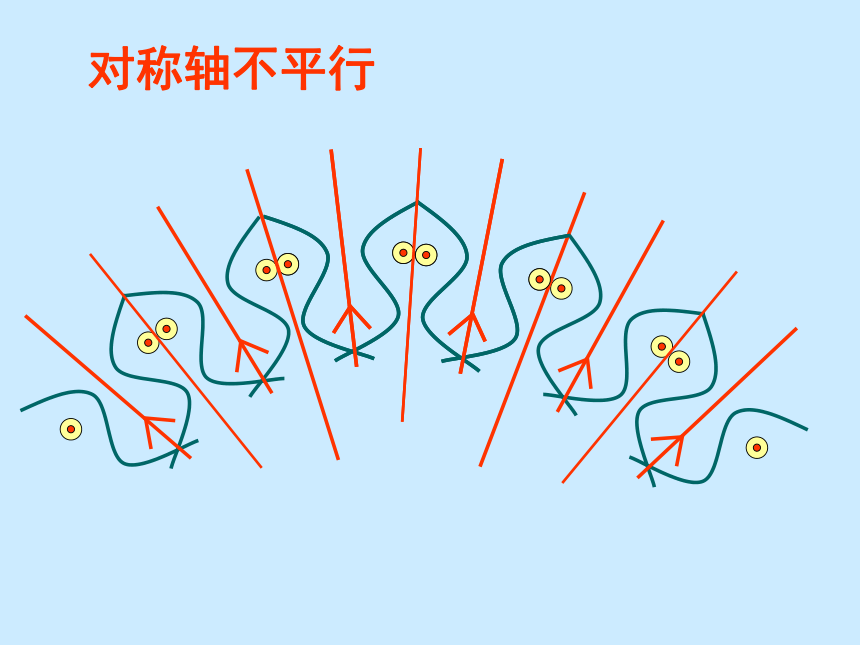
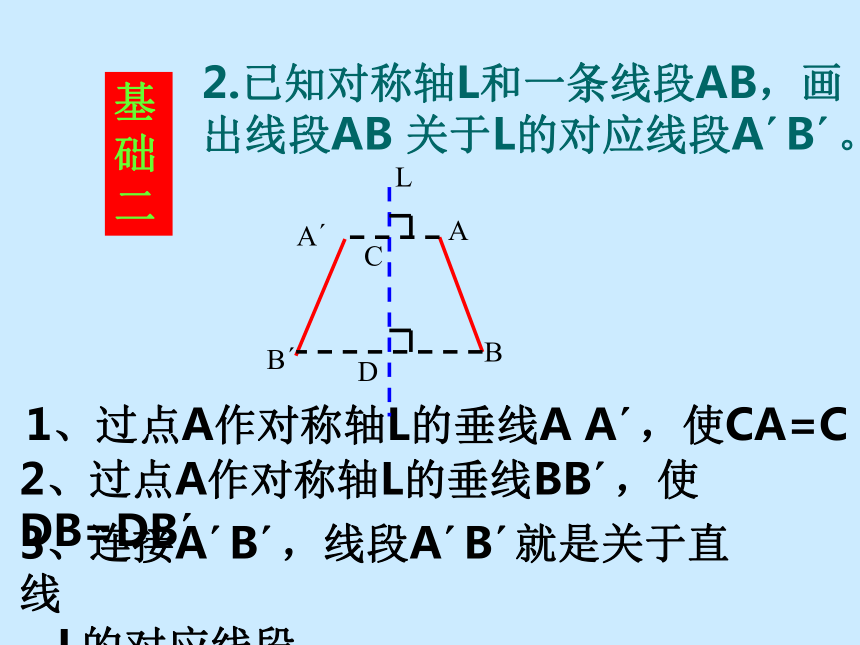
并创造次序、美丽和完善…… ------赫尔曼·外尔 12.2 .1作轴对称图形动手试一试一 张半透明的纸的左边画有一只左脚印,把这张纸对折后描图,打开对折的纸。就能得到相应的右脚印动脑想一 想左脚印和右脚印有什么关系?成轴对称对称轴是:折痕所在的 直线,即直线 l 。图中的pp’与直线l是什么关系?线段pp’被直线l垂直平分类似地,我们可由一个图形得到与它成轴对称的另一个图形,重复此过程,可得到美丽的图案用心看一看图案是怎样得到的?对称轴平行对称轴不平行①对称轴方向和位置发生变化时,得到的图形的方向和位置也 会发生变化。②由一个平面图形可以得到它关于一条直线L对称的图形,这个图形与原图形的形状、大小完全一样;③新图形上的每一点,都是原图形上的某一点关于直线L的对称点;④连接任意一 对对于的对应点的线段被对称轴垂直平分。小结:一个轴对称图形也可以看作以他的一部分为基础,经轴对称变换扩展而成的。 成轴对称的两个图形中的任何一个可以看作由另一个图形经过轴对称变换后得到。1、过点A作对称轴L的垂线A A′,使CA=C A′2.已知对称轴L和一条线段AB,画出线段AB 关于L的对应线段A′B′。ABA′B′L2、过点A作对称轴L的垂线BB′,使DB=DB′3、连接A′B′,线段A′B′就是关于直线
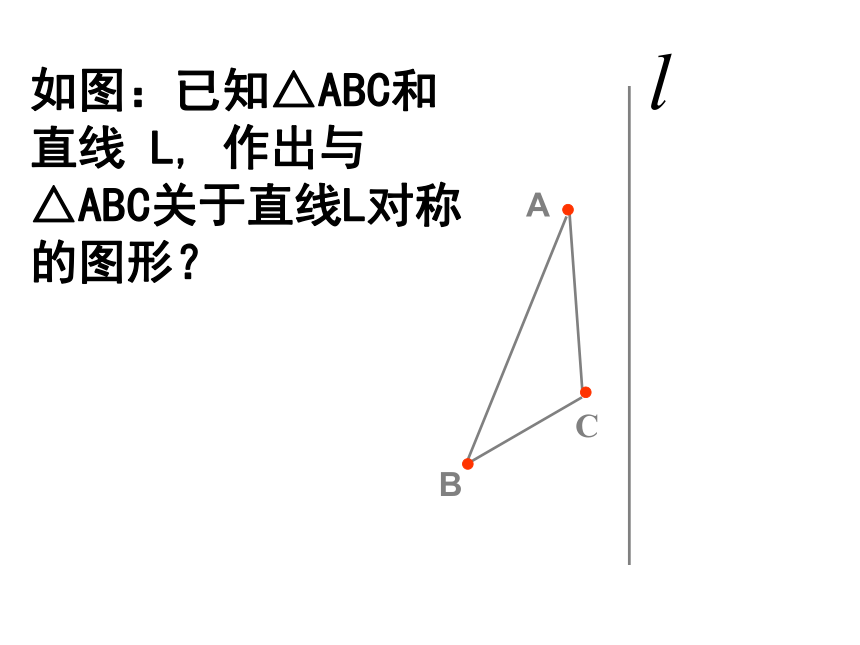
L的对应线段CD基础二如图:已知△ABC和直线 L, 作出与△ABC关于直线L对称的图形?B找关键点作出其对称点,
顺次连结线段构成三角形.AB如图:
已知△ABC和直线 L, 作出与△ABC关于直线L对称的图形?C如图给出了一个图案的一半,其中的直线 是这个图案的对称轴.
(1)整个图案是个什么形状?
(2)请准确地画出它的另一半.2、下图是在方格纸上画出的一半,以树干为对称轴画出数的另一半。3.下面的第二个时间可由第一个怎样变换而得到(四)镜面、水面与轴对称4. 如图所示的是在一面镜子里看到的一个算式,该算式的实际情况是怎样的?演示(二)数形结合,利用轴对称找规律5. 如图,是一只停泊在平静水面上的小船,它的“倒影”应是图中的( ).B演示试一试:6、一次晚会上,主持人出了一道题目:“如何 变成一个真正的等式“,很长时间没有人答出,小兰仅仅拿出了一面镜子,就很快解决了这道题目,你知道她是怎样做的吗?演示例5.如图所示,把一个正方形三次对折后沿虚 线剪下一角,则展开后所得的图形是( ). 轴对称图形的还原问题演示例9.晓慧同学学习了轴对称知识后,忽然想起来过去做过的一道题:有一组数排列成方阵,如下图所示,试计算这组数的和.晓慧想方阵就像正方形,正方形是轴对称图形,能不能利用轴对称的思想来解决方阵的计算问题呢?晓慧试了试,竟得到了非常巧妙的方法,你也能试试看吗?解题要点:将对角线上的5看作是对称轴,将正方形对折,对称位置上的两个数之和都是10,从而使问题简单化. 解题启示:
在求一组有规律的数的和时,经常会用到对称思想.解:方阵中数的和=10×10+5×5=125.
张店区政府为了方便居民的生活,计划在三个住宅小区A、B、C之间修建一个购物中心,试问,该购物中心应建于何处,才能使得它到三个小区的距离相等。ABC实际问题12、如图,在直线L上求作一点P,使PA=PB.LAB实际问题2PA=PB数学问题源于生活实践,反过来数学又为生活实践服务OAB. M. N3、有两条公路OA,OB,两个村庄M、N。你能选择一个纺织厂的厂址P,使P到公路的距离相等,且使M、N两村的工人上下班的路程一样吗?问题探讨思维点拨:与M、N两点的距离相等,说明要找的点在线段MN的垂直平分线上;
到∠AOB两边的距离相等,说明要找的点又在∠AOB的平分线上.
故符合条件的点是MN的垂直平分线与∠AOB的平分线的交点. 到达目的地可能有很多条路,能找出一条合理的路径,并解释为什么合理,这就是人的智慧的展现。如图,有一个小和尚住在A处,B处是一所庙宇。B理由:两点之间线段最短。问题(1) 若小和尚每天要从住处A出发直接送东西去B处,他该怎么走路程最短呢?∴线段AB就是所走的最短路程。问题(2) 若在A与B之间有一条小河L,有一天,方丈要求小和尚先从住处A出发到河边L取水,再把水送到庙宇B,小和尚该如何走,使走的路程最短呢?BLP∴他沿A→P→B走是最短路程。思路:将不同线的三点转化为同线的三点。问题(3) 若在A与B同侧有一条小河L,方丈还是要求小和尚先从住处A出发到河边取水,再送到庙宇B,小和尚又该如何走,使走的路程最短呢?BLPA’∴他沿A→P→B走是最短路程。思路:利用轴对称将点同侧变异侧求线段和最短。思考与拓展: 问题(4)方丈比较喜欢数学,现在他将A,B两个点放在平面直角坐标系中,得A(1,1),B(5,3),且记小河为X轴,若方丈还是要求小和尚先去河边取水,再送到B,为了使自己走的路程最短,小和尚该如何确定取水点坐标? AB012345-3-2-1XY54321-1-2AP思考与拓展: (4)现在庙宇B的旁边又多了一所小庙宇C,方丈还是要求小和尚先去河边取水,再送到B,然后送到C,最后回到A,此时,小和尚又该怎么走路程最短呢? ABCL思路:将陌生问题转化为熟悉问题。PA’ 问题(5) 有一天,方丈没有任务交给小和尚去做,此时,小和尚想先去住处A边的长街M买东西,再到河边取水,然后回到A,小和尚又该怎么走,使一天走的路程最短呢?LM思考与拓展: 通过我们帮小和尚进行路径的合理选择,你能谈谈我们都用了哪些数学知识? 课堂总结: (1)两点之间线段最短。 (2)三角形中任意两边之和大于第三边。 (4)线段垂直平分线的性质。 (3)轴对称变换的知识。 从中你又学到了什么数学思想? 转化思想。 练习1:
如图,要在燃气管道L上修建一个泵站 ,分别向A,B两镇供气。泵站应修在管道的什么地方,可使所用的输气管线最短?LAB练习2.如图1,某公路的同一侧有A、B、C三个村庄,要在公路边建一货栈D,向A、B、C三个村庄送农用物资,路线是:D→A→B→C→D和D→C→B→A→D.1.试问在公路边上是否存在一点D,使送货路程最短?(把公路边近似看作公路上)
2.将A、B、C三点放在平面直角坐标系中,把x轴建立在公路上,坐标如图所示.请画出D点所在的位置,并写出画法.
3.求出D点在该坐标系中的坐标(要求有运算过程)
3. 利用轴对称解决线路最短问题 分析:要求送货路程最短,实质就是要AD+CD最小. 思维点拨:
(1)存在;
(2)作点A关于x轴的对称点A’,
连结A’C与x轴的交点即为点D;
(3)先用待定系数法求出直线A’C
的解析式,再求D点的坐标.
D(3,0) 例7.如图,在锐角∠AOB内有一定点P,试在OA、OB上确定两点C、D,使△PCD的周长最短. ……2. 利用轴对称解决周长最小问题 如图:A为马厩,B为帐篷牧马人某一天要从马厩牵出马,先到草地边某一处牧马,再到河边饮马,然后回到帐篷.请你帮他确定这一天的最短路线.请你帮忙例8.如图1,A为厩,B为帐篷,牧马人某一天要从马厩牵出马,先到草地某一处牧马,再到河边饮马,然后回到帐篷.请你帮他确定这一天的最短路线.分析:本题的实质是在MN上确定一点(如C),在NH上确定一点(如D),使AC+CD+DB最小.可利用轴对称解决问题.作业:
再见例12.如图,在平面直角坐标系中,
点P(2,3),Q(3,2),请在x轴和
y轴上分别找到M点和N点,使四边形PQMN周长最小.
(1)作出M点和N点.
(2)求出M点和N点的坐标.解(1)略
(2)直线P1Q1的解析式为:y=-x+1
M(1,0),N(0,1)//
并创造次序、美丽和完善…… ------赫尔曼·外尔 12.2 .1作轴对称图形动手试一试一 张半透明的纸的左边画有一只左脚印,把这张纸对折后描图,打开对折的纸。就能得到相应的右脚印动脑想一 想左脚印和右脚印有什么关系?成轴对称对称轴是:折痕所在的 直线,即直线 l 。图中的pp’与直线l是什么关系?线段pp’被直线l垂直平分类似地,我们可由一个图形得到与它成轴对称的另一个图形,重复此过程,可得到美丽的图案用心看一看图案是怎样得到的?对称轴平行对称轴不平行①对称轴方向和位置发生变化时,得到的图形的方向和位置也 会发生变化。②由一个平面图形可以得到它关于一条直线L对称的图形,这个图形与原图形的形状、大小完全一样;③新图形上的每一点,都是原图形上的某一点关于直线L的对称点;④连接任意一 对对于的对应点的线段被对称轴垂直平分。小结:一个轴对称图形也可以看作以他的一部分为基础,经轴对称变换扩展而成的。 成轴对称的两个图形中的任何一个可以看作由另一个图形经过轴对称变换后得到。1、过点A作对称轴L的垂线A A′,使CA=C A′2.已知对称轴L和一条线段AB,画出线段AB 关于L的对应线段A′B′。ABA′B′L2、过点A作对称轴L的垂线BB′,使DB=DB′3、连接A′B′,线段A′B′就是关于直线
L的对应线段CD基础二如图:已知△ABC和直线 L, 作出与△ABC关于直线L对称的图形?B找关键点作出其对称点,
顺次连结线段构成三角形.AB如图:
已知△ABC和直线 L, 作出与△ABC关于直线L对称的图形?C如图给出了一个图案的一半,其中的直线 是这个图案的对称轴.
(1)整个图案是个什么形状?
(2)请准确地画出它的另一半.2、下图是在方格纸上画出的一半,以树干为对称轴画出数的另一半。3.下面的第二个时间可由第一个怎样变换而得到(四)镜面、水面与轴对称4. 如图所示的是在一面镜子里看到的一个算式,该算式的实际情况是怎样的?演示(二)数形结合,利用轴对称找规律5. 如图,是一只停泊在平静水面上的小船,它的“倒影”应是图中的( ).B演示试一试:6、一次晚会上,主持人出了一道题目:“如何 变成一个真正的等式“,很长时间没有人答出,小兰仅仅拿出了一面镜子,就很快解决了这道题目,你知道她是怎样做的吗?演示例5.如图所示,把一个正方形三次对折后沿虚 线剪下一角,则展开后所得的图形是( ). 轴对称图形的还原问题演示例9.晓慧同学学习了轴对称知识后,忽然想起来过去做过的一道题:有一组数排列成方阵,如下图所示,试计算这组数的和.晓慧想方阵就像正方形,正方形是轴对称图形,能不能利用轴对称的思想来解决方阵的计算问题呢?晓慧试了试,竟得到了非常巧妙的方法,你也能试试看吗?解题要点:将对角线上的5看作是对称轴,将正方形对折,对称位置上的两个数之和都是10,从而使问题简单化. 解题启示:
在求一组有规律的数的和时,经常会用到对称思想.解:方阵中数的和=10×10+5×5=125.
张店区政府为了方便居民的生活,计划在三个住宅小区A、B、C之间修建一个购物中心,试问,该购物中心应建于何处,才能使得它到三个小区的距离相等。ABC实际问题12、如图,在直线L上求作一点P,使PA=PB.LAB实际问题2PA=PB数学问题源于生活实践,反过来数学又为生活实践服务OAB. M. N3、有两条公路OA,OB,两个村庄M、N。你能选择一个纺织厂的厂址P,使P到公路的距离相等,且使M、N两村的工人上下班的路程一样吗?问题探讨思维点拨:与M、N两点的距离相等,说明要找的点在线段MN的垂直平分线上;
到∠AOB两边的距离相等,说明要找的点又在∠AOB的平分线上.
故符合条件的点是MN的垂直平分线与∠AOB的平分线的交点. 到达目的地可能有很多条路,能找出一条合理的路径,并解释为什么合理,这就是人的智慧的展现。如图,有一个小和尚住在A处,B处是一所庙宇。B理由:两点之间线段最短。问题(1) 若小和尚每天要从住处A出发直接送东西去B处,他该怎么走路程最短呢?∴线段AB就是所走的最短路程。问题(2) 若在A与B之间有一条小河L,有一天,方丈要求小和尚先从住处A出发到河边L取水,再把水送到庙宇B,小和尚该如何走,使走的路程最短呢?BLP∴他沿A→P→B走是最短路程。思路:将不同线的三点转化为同线的三点。问题(3) 若在A与B同侧有一条小河L,方丈还是要求小和尚先从住处A出发到河边取水,再送到庙宇B,小和尚又该如何走,使走的路程最短呢?BLPA’∴他沿A→P→B走是最短路程。思路:利用轴对称将点同侧变异侧求线段和最短。思考与拓展: 问题(4)方丈比较喜欢数学,现在他将A,B两个点放在平面直角坐标系中,得A(1,1),B(5,3),且记小河为X轴,若方丈还是要求小和尚先去河边取水,再送到B,为了使自己走的路程最短,小和尚该如何确定取水点坐标? AB012345-3-2-1XY54321-1-2AP思考与拓展: (4)现在庙宇B的旁边又多了一所小庙宇C,方丈还是要求小和尚先去河边取水,再送到B,然后送到C,最后回到A,此时,小和尚又该怎么走路程最短呢? ABCL思路:将陌生问题转化为熟悉问题。PA’ 问题(5) 有一天,方丈没有任务交给小和尚去做,此时,小和尚想先去住处A边的长街M买东西,再到河边取水,然后回到A,小和尚又该怎么走,使一天走的路程最短呢?LM思考与拓展: 通过我们帮小和尚进行路径的合理选择,你能谈谈我们都用了哪些数学知识? 课堂总结: (1)两点之间线段最短。 (2)三角形中任意两边之和大于第三边。 (4)线段垂直平分线的性质。 (3)轴对称变换的知识。 从中你又学到了什么数学思想? 转化思想。 练习1:
如图,要在燃气管道L上修建一个泵站 ,分别向A,B两镇供气。泵站应修在管道的什么地方,可使所用的输气管线最短?LAB练习2.如图1,某公路的同一侧有A、B、C三个村庄,要在公路边建一货栈D,向A、B、C三个村庄送农用物资,路线是:D→A→B→C→D和D→C→B→A→D.1.试问在公路边上是否存在一点D,使送货路程最短?(把公路边近似看作公路上)
2.将A、B、C三点放在平面直角坐标系中,把x轴建立在公路上,坐标如图所示.请画出D点所在的位置,并写出画法.
3.求出D点在该坐标系中的坐标(要求有运算过程)
3. 利用轴对称解决线路最短问题 分析:要求送货路程最短,实质就是要AD+CD最小. 思维点拨:
(1)存在;
(2)作点A关于x轴的对称点A’,
连结A’C与x轴的交点即为点D;
(3)先用待定系数法求出直线A’C
的解析式,再求D点的坐标.
D(3,0) 例7.如图,在锐角∠AOB内有一定点P,试在OA、OB上确定两点C、D,使△PCD的周长最短. ……2. 利用轴对称解决周长最小问题 如图:A为马厩,B为帐篷牧马人某一天要从马厩牵出马,先到草地边某一处牧马,再到河边饮马,然后回到帐篷.请你帮他确定这一天的最短路线.请你帮忙例8.如图1,A为厩,B为帐篷,牧马人某一天要从马厩牵出马,先到草地某一处牧马,再到河边饮马,然后回到帐篷.请你帮他确定这一天的最短路线.分析:本题的实质是在MN上确定一点(如C),在NH上确定一点(如D),使AC+CD+DB最小.可利用轴对称解决问题.作业:
再见例12.如图,在平面直角坐标系中,
点P(2,3),Q(3,2),请在x轴和
y轴上分别找到M点和N点,使四边形PQMN周长最小.
(1)作出M点和N点.
(2)求出M点和N点的坐标.解(1)略
(2)直线P1Q1的解析式为:y=-x+1
M(1,0),N(0,1)//
