2024学年新教科版高一物理必修一第二章第三节2.3匀变速直线运动的位移与时间的关系 课件(14页)
文档属性
| 名称 | 2024学年新教科版高一物理必修一第二章第三节2.3匀变速直线运动的位移与时间的关系 课件(14页) |  | |
| 格式 | pptx | ||
| 文件大小 | 10.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 教科版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2024-08-19 14:47:06 | ||
图片预览






文档简介
(共14张PPT)
第二章第3节
匀变速直线运动
位移与时间的关系
匀速直线运动的位移
位移公式
公式法
v – t 图线的面积表示位移
图象法
v/m.s-1
3
2
1
0
1
2
3
4
t/s
5
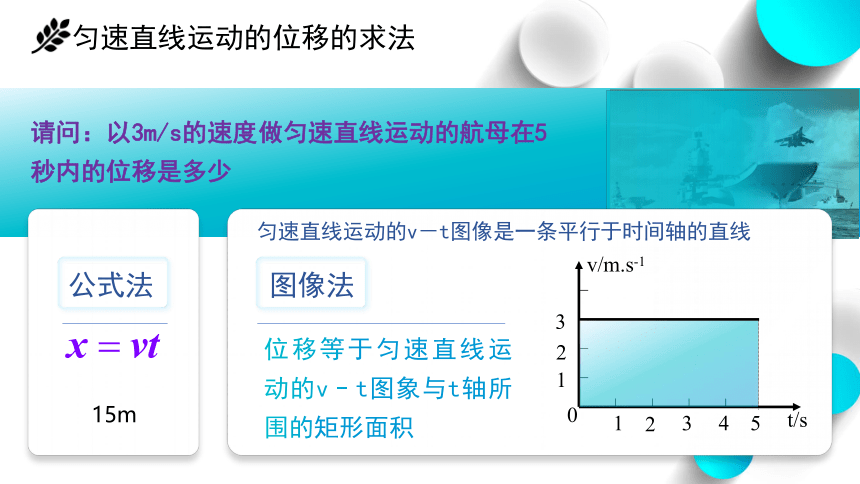
匀速直线运动的位移的求法
v/m.s-1
3
2
1
0
1
2
3
4
t/s
5
匀速直线运动的v-t图像是一条平行于时间轴的直线
位移等于匀速直线运动的v–t图象与t轴所围的矩形面积
公式法
图像法
15m
请问:以3m/s的速度做匀速直线运动的航母在5秒内的位移是多少
想一想:当速度为正值和为负值时,位移有什么不同?
v/m·s-1
t/s
2
6
4
3
4
0
2
1
-2
-4
x
X1
X2
5
7
8
9
6
面积也有正负
X1
X2
面积
表示位移的方向为正方向
面积
表示位移的方向为负方向
正
负
X1
X2
猜想:能!
思考
匀变速直线运动的位移是否也有类似的关系
是否也可以用v-t图象与t轴所围的“面积”表示呢?
匀速直线运动的v–t 图象与t轴所围的矩形“面积”就等于“位移”
v/m.s-1
3
2
1
0
1
2
3
4
t/s
5
v0
v
0
t
v0
v
0
t
v0
v
0
t
v0
v
0
t
t时间内位移等于图像中的梯形面积
探究用v-t图像能否表示匀变速直线运动的位移
50%
70%
90%
100%
时间轴无限分割
假如把时间轴无限分割,情况会怎么样呢?
微元求和
在每一小段内,可粗略认为物体做匀速直线运动
各段位移可以用一个又窄又高的小矩形的面积代表
小矩形的面积之和近似地代表物体在整个运动过程中的位移
A
A′
B′
B
C
C′
D
D′
?
v0
v
t
O
t
t1
t2
t3
O
t
t1
t2
t3
t4
t5
t6
t7
假如把时间轴无限分割,情况会怎么样呢?
面积
v (m/s)
t (s)
v (m/s)
t (s)
v (m/s)
t (s)
粗略地表示位移
较精确地表示位移
由图可知:梯形OABC的面积
S=(OC+AB)×OA/2
v=v0+at
推导匀变速直线运动的位移公式
位移公式推导
C
B
A
得:
代入各物理量得:
又
匀变速直线运动v-t图像
(位移方程)
匀变速直线运动的位移
匀变速直线运动的位移方程
选正方向
矢量式
时间间隔
两种特殊形式
初速度为零的匀加速直线运动
匀速直线运动
1
2
位移
初速度
加速度
单位
统一
第二章第3节
匀变速直线运动
位移与时间的关系
匀速直线运动的位移
位移公式
公式法
v – t 图线的面积表示位移
图象法
v/m.s-1
3
2
1
0
1
2
3
4
t/s
5
匀速直线运动的位移的求法
v/m.s-1
3
2
1
0
1
2
3
4
t/s
5
匀速直线运动的v-t图像是一条平行于时间轴的直线
位移等于匀速直线运动的v–t图象与t轴所围的矩形面积
公式法
图像法
15m
请问:以3m/s的速度做匀速直线运动的航母在5秒内的位移是多少
想一想:当速度为正值和为负值时,位移有什么不同?
v/m·s-1
t/s
2
6
4
3
4
0
2
1
-2
-4
x
X1
X2
5
7
8
9
6
面积也有正负
X1
X2
面积
表示位移的方向为正方向
面积
表示位移的方向为负方向
正
负
X1
X2
猜想:能!
思考
匀变速直线运动的位移是否也有类似的关系
是否也可以用v-t图象与t轴所围的“面积”表示呢?
匀速直线运动的v–t 图象与t轴所围的矩形“面积”就等于“位移”
v/m.s-1
3
2
1
0
1
2
3
4
t/s
5
v0
v
0
t
v0
v
0
t
v0
v
0
t
v0
v
0
t
t时间内位移等于图像中的梯形面积
探究用v-t图像能否表示匀变速直线运动的位移
50%
70%
90%
100%
时间轴无限分割
假如把时间轴无限分割,情况会怎么样呢?
微元求和
在每一小段内,可粗略认为物体做匀速直线运动
各段位移可以用一个又窄又高的小矩形的面积代表
小矩形的面积之和近似地代表物体在整个运动过程中的位移
A
A′
B′
B
C
C′
D
D′
?
v0
v
t
O
t
t1
t2
t3
O
t
t1
t2
t3
t4
t5
t6
t7
假如把时间轴无限分割,情况会怎么样呢?
面积
v (m/s)
t (s)
v (m/s)
t (s)
v (m/s)
t (s)
粗略地表示位移
较精确地表示位移
由图可知:梯形OABC的面积
S=(OC+AB)×OA/2
v=v0+at
推导匀变速直线运动的位移公式
位移公式推导
C
B
A
得:
代入各物理量得:
又
匀变速直线运动v-t图像
(位移方程)
匀变速直线运动的位移
匀变速直线运动的位移方程
选正方向
矢量式
时间间隔
两种特殊形式
初速度为零的匀加速直线运动
匀速直线运动
1
2
位移
初速度
加速度
单位
统一
同课章节目录
- 第一章 描述运动的基本概念
- 1 参考系 时间 质点
- 2 位置 位移
- 3 位置变化的快慢与方向——速度
- 4 实验:用打点计时器测量小车的速度
- 5 速度变化的快慢与方向——加速度
- 第二章 匀变速直线运动的规律
- 1 匀变速直线运动的研究
- 2 匀变速直线运动速度与时间的关系
- 3 匀变速直线运动位移与时间的关系
- 4 匀变速直线运动规律的应用
- 5 自由落体运动
- 第三章 相互作用
- 1 力 重力
- 2 弹力
- 3 摩擦力
- 4 力的合成
- 5 力的分解
- 6 共点力作用下物体的平衡
- 第四章 牛顿运动定律
- 1 牛顿第一定律
- 2 探究加速度与力、质量的关系
- 3 牛顿第二定律
- 4 力学单位制
- 5 牛顿第三定律
- 6 牛顿运动定律的应用
- 7 超重与失重
