人教版数学八年级上册12.1全等三角形 精品同步练习(含解析)
文档属性
| 名称 | 人教版数学八年级上册12.1全等三角形 精品同步练习(含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-16 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
人教版八年级上册数学 12.1全等三角形 同步练习
(考试时间:60分钟 满分:100分)
选择题(本大题共10小题,每小题3分,共30分。下列各题的备选答案中,只有一项是最符合题意的,请选出。)
1.下列四组图形中,是全等图形的一组是
A. B.
C. D.
2.如下图,已知△ABE≌△ACD,∠1=∠2,∠B=∠C,不正确的等式是
A.AB=AC B.∠BAE=∠CAD
C.BE=DC D.AD=DE
3.若△ABC≌△DEF,且△ABC的周长为20,AB=5,BC=8,则DF=
A.5 B.8
C.7 D.5或8
4.如图,△ABF≌△CDE,则
A.∠B=∠ECD B.∠A=∠ECD
C.AF=CE D.AB=CE
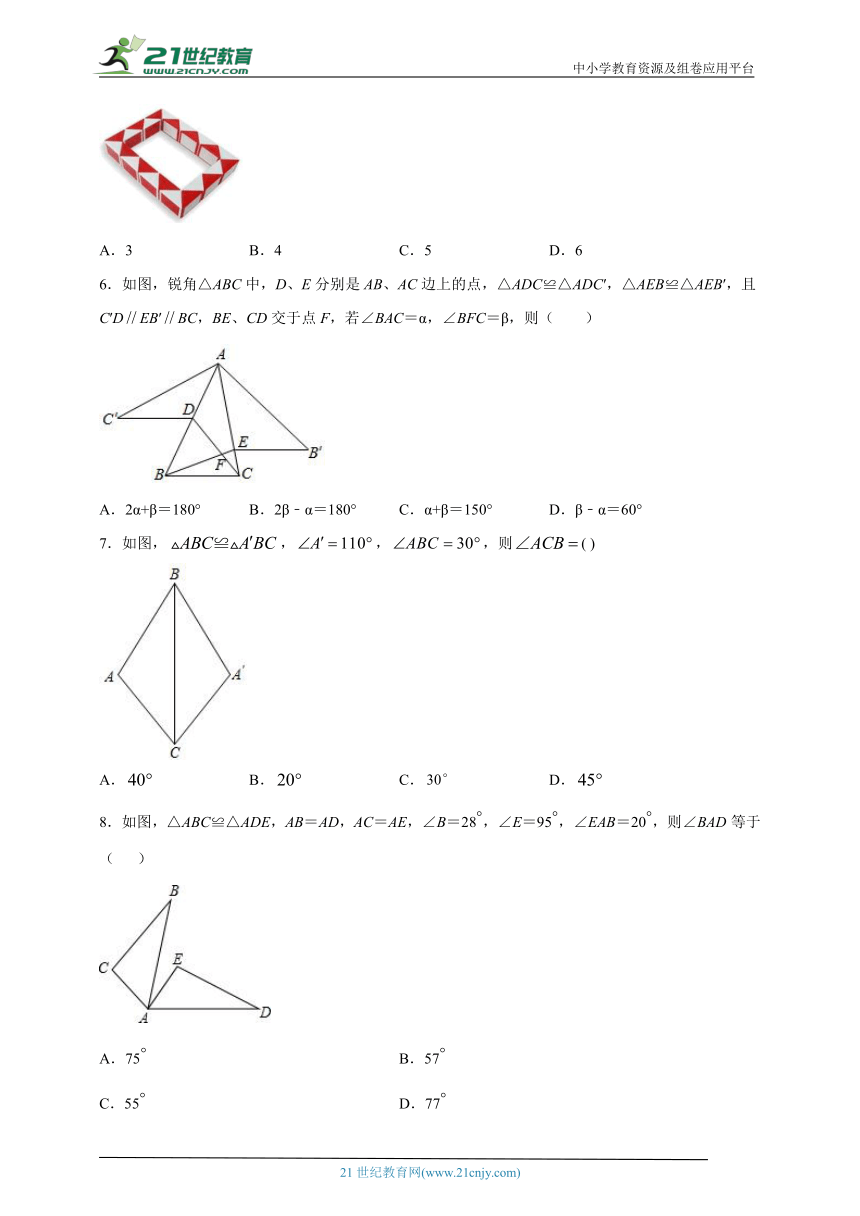
5.百变魔尺,魅力无穷,如图是用24段魔尺(24个等腰直角三角形,把等腰直角三角形最长边看做1)围成的长为4宽为3的长方形.用该魔尺能围出不全等的长方形个数为( )
A.3 B.4 C.5 D.6
6.如图,锐角△ABC中,D、E分别是AB、AC边上的点,△ADC≌△ADC′,△AEB≌△AEB′,且C′DEB′BC,BE、CD交于点F,若∠BAC=α,∠BFC=β,则( )
A.2α+β=180° B.2β﹣α=180° C.α+β=150° D.β﹣α=60°
7.如图,,,,则( )
A. B. C. D.
8.如图,△ABC≌△ADE,AB=AD,AC=AE,∠B=28,∠E=95,∠EAB=20,则∠BAD等于( )
A.75 B.57
C.55 D.77
9.下列命题的逆命题是真命题的是( )
A.两个全等三角形的对应角相等
B.若一个三角形的两个内角分别为和,则这个三角形是直角三角形
C.两个全等三角形的面积相等
D.如果一个数是无限不循环小数,那么这个数是无理数
10.下列命题的逆命题是真命题的是( ).
A.的平方根是3 B.是无理数
C.1的立方根是1 D.全等三角形的周长相等
填空题(本大题共5小题,每小题4分,共20分。)
11.如图,将△ABC沿BC所在的直线平移到△A'B'C'的位置,则△ABC__________△A'B'C',图中∠A与__________,∠B与__________,∠ACB与__________是对应角.
12.如图,两个三角形全等,其中已知某些边的长度和某些角的度数,则x=__________.
13.如图,,点、、、在同一条直线上,、交于点,,则的度数是______°.
14.如图,,,,,则______.
15.如图,,B、E、C、F在同一直线上,,,则CF的长为___________.
三、解答题(本大题共5小题,每小题10分,共50分。解答应写出文字说明、证明过程或演算步骤.)
16.如图,已知△ABC≌△EDC,指出其对应边和对应角.
17.在的方格纸中,每格的边长为1,请按下列要求画图.
(1)在图1中画一个格点,使与全等,且所画格点三角形的顶点均不与点B,C重合.
(2)在图2中画一个面积为7的格点四边形,且为锐角.
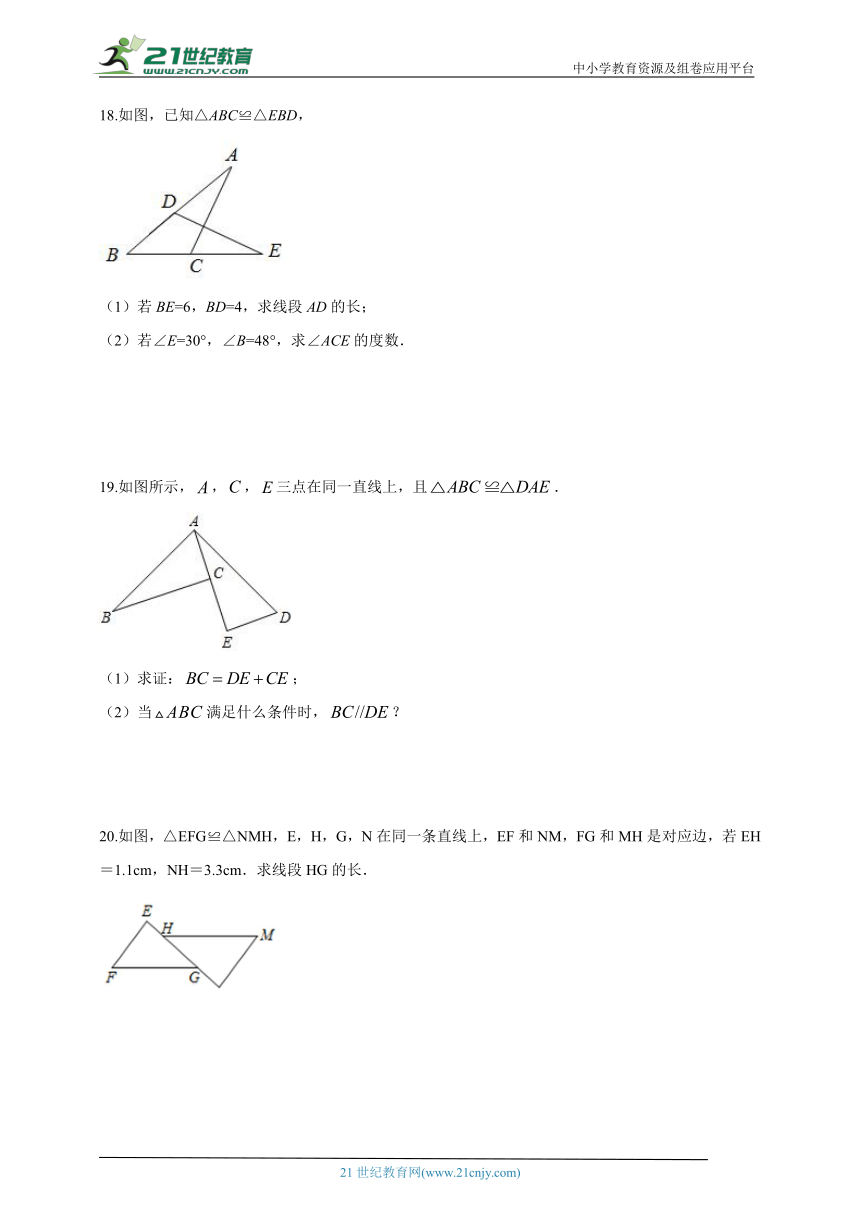
18.如图,已知△ABC≌△EBD,
(1)若BE=6,BD=4,求线段AD的长;
(2)若∠E=30°,∠B=48°,求∠ACE的度数.
19.如图所示,,,三点在同一直线上,且.
(1)求证:;
(2)当满足什么条件时,?
20.如图,△EFG≌△NMH,E,H,G,N在同一条直线上,EF和NM,FG和MH是对应边,若EH=1.1cm,NH=3.3cm.求线段HG的长.
参考答案
选择题
1.【答案】D
【解析】由全等形的概念可知:A、B中的两个图形大小不同,C中的形状不同,D则完全相同.故选D.
2.【答案】D
【解析】由于△ABE≌△ACD,所以对应边、对应角都相等,A、B、C三项正确,而AD和AE是相等的,所以D项是错误的.故选D.
3.【答案】C
【解析】∵△ABC的周长为20,AB=5,BC=8,∴AC=7,∵△ABC≌△DEF,∴DF=AC=7,故选C.
4.【答案】C
【解析】∵△ABF≌△CDE,∴∠B=∠D,AF=CE,AB=CD,而顶点A处不能用一个大写字母表示任何一个角,故选C.
5.【答案】A
【分析】根据14=(1+6)×2=(2+5)×2=(3+4)×2,可知能围出不全等的长方形有3个.
【详解】∵长为4、宽为3的长方形,
∴周长为2×(3+4)=14
14=(1+6)×2=(2+5)×2=(3+4)×2,
∴能围出不全等的长方形有3个,
故选:A.
6.【答案】A
【分析】延长C′D交AC于M,如图,根据全等的性质得∠C′=∠ACD,∠C′AD=∠CAD=∠B′AE=α,再利用三角形外角性质得∠C′MC=∠C′+∠C′AM=∠C′+2α,接着利用C′D∥B′E得到∠AEB=∠C′MC,而根据三角形内角和定理,三角形外角性质和等角代换,进一步变形后即可得到答案.
【详解】延长C′D交AC于M,如图,
∵△ADC≌△ADC′,△AEB≌△AEB′,
∴∠C′=∠ACD,∠C′AD=∠CAD=∠B′AE=α,
∴∠C′MC=∠C′+∠C′AM=∠C′+2α,
∵C′D∥B′E,
∴∠AEB′=∠C′MC,
∵∠AEB′=180°﹣∠B′﹣∠B′AE=180°﹣∠B′﹣α,
∴∠C′+2α=180°﹣∠B′﹣α,
∴∠C′+∠B′=180°﹣3α,
∵β=∠BFC=∠BDF+∠DBF
=∠DAC+∠ACD+∠B'
=α+∠ACD+∠B′=α+∠C′+∠B′
=α+180°﹣3α=180°﹣2α,
即:2α+β=180°.
故选:A.
7.【答案】A
【分析】根据全等三角形对应角相等即可求解;
【详解】∵ ,
∴ ∠A=∠=110°,
∵∠ABC=30°,
∴∠ACB=180°-110°-30°=40°,
故选:A.
8.【答案】D
【分析】先根据全等三角形的对应角相等得出∠B=∠D=28°,再由三角形内角和为180°,求出∠DAE=57°,然后根据∠BAD=∠DAE+∠EAB即可得出∠BAD的度数.
【详解】∵△ABC≌△ADE,
∴∠B=∠D=28°,
又∵∠D+∠E+∠DAE=180°,∠E=95°,
∴∠DAE=180°-28°-95°=57°,
∵∠EAB=20°,
∴∠BAD=∠DAE+∠EAB=77°.
故选:D.
9.【答案】D
【分析】根据原命题分别写出逆命题,然后再判断真假即可.
【详解】A、两个全等三角形的对应角相等,
逆命题是:对应角相等的两个三角形全等,是假命题;
B、若一个三角形的两个内角分别为 30° 和 60° ,则这个三角形是直角三角形,
逆命题是:如果一个三角形是直角三角形,那么它的两个内角分别为 30° 和 60° ,是假命题;
C、两个全等三角形的面积相等,
逆命题是:面积相等的两个三角形全等,是假命题;
D、如果一个数是无限不循环小数,那么这个数是无理数,
逆命题是:如果一个数是无理数,那么这个数是无限不循环小数 ,是真命题.
故选:D
10.【答案】C
【分析】根据把一个命题的条件和结论互换就得到它的逆命题,先得出逆命题,再进行判断即可.
【详解】A、的平方根是3的逆命题是:3是的平方根,是假命题;
B、是无理数的逆命题是:无理数是,是假命题;
C、1的立方根是1的逆命题是:1是1的立方根,是真命题;
D、全等三角形的周长相等的逆命题是:周长相等的三角形全等,是假命题;
故选:C.
填空题
11.【答案】≌;∠A';∠A'B'C';∠C'
【解析】∵△ABC沿BC所在的直线平移到△A'B'C'的位置,∴△ABC≌△A'B'C',∴∠A=∠A',∠B=
∠A'B'C',∠ACB=∠C',∴∠A与∠A',∠B与∠A'B'C',∠ACB与∠C'是对应角,
故答案为:≌;∠A';∠A'B'C';∠C'.
12.【答案】60°
【解析】△ABC中,∠C=180°-65°-55°=60°,根据全等三角形的对应角相等可知x=60°.故答案为:60°.
13.【答案】60
【分析】根据全等三角形的性质得到∠DFE=∠ACB=30°,根据三角形的外角性质计算,得到答案.
【详解】∵△ABC≌△DEF,
∴∠DFE=∠ACB=30°,
∵∠AMF是△MFC的一个外角,
∴∠AMF=∠DFE+∠ACB=60°,
故答案为:60.
14.【答案】3
【分析】根据全等三角形对应边相等可得AC=BD,再求出AB=CD,然后代入数据进行计算即可得解.
【详解】∵△ACE≌△DBF,
∴AC=DB,
∴AC-BC=BD-BC,
即AB=CD,
∵AD=8,BC=2,
∴AB=(AD-BC)=×(8-2)=3.
故答案为:3.
15.【答案】3
【分析】直接用全等三角形的性质可得CF=EF-CE=BC-CE,然后进行求解即可;
【详解】∵△ABC≌△DEF,
∴ BC=EF,
∵ BC=7,EC=4,
∴ CF=7-4=3,
故答案为:3.
解答题
16.【解析】∵△ABC≌△EDC,
∴AB的对应边是ED,AC的对应边是EC,BC的对应边是DC,
∠A的对应角是∠E,∠B的对应角是∠D,∠ACB的对应角是∠ECD.
17.【答案】(1)见解析;(2)见解析
【分析】(1)利用轴对称的性质解决问题即可.
(2)构造梯形,利用数形结合的思想解决问题即可.
【详解】(1)如图1中,△ADE即为所求.
(2)如图2中,四边形ABCD即为所求.
18.【答案】(1)2;(2)78°.
【分析】(1)根据△ABC≌△EBD,得AB=BE=6,根据AD=AB-BD计算即可;
(2)根据△ABC≌△EBD,得∠A=30°,利用∠ACE=∠A+∠B计算即可.
【详解】(1)∵△ABC≌△EBD,
∴AB=BE=6,
∵AD=AB-BD,BD=4,
∴AD=6-4=2;
(2)∵△ABC≌△EBD,
∴∠A=∠E=30°,
∵∠ACE=∠A+∠B,∠B=48°,
∴∠ACE=30°+48°
=78°.
19.【答案】(1)证明见解析;(2)为直角时,
【分析】(1)根据全等三角形的性质求出BD=AE,AD=CE,代入求出即可;
2)根据全等三角形的性质求出∠E=∠BDA= ,推出∠BDE= ,根据平行线的判定求出即可.
【详解】(1)证明:∵,
∴AE=BC,AC=DE,
又∵,
∴.
(2)若,则,
又∵,
∴,
∴,
又∵,
∴,
即当满足为直角时,.
20.【答案】2.2 cm
【分析】根据,可得,从而有,再计算HG的长即可.
【详解】(1),EF和NM,FG和MH是对应边,
,
,
又EH=1.1cm,NH=3.3cm,
cm,
答:线段HG的长为2.2 cm;
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
人教版八年级上册数学 12.1全等三角形 同步练习
(考试时间:60分钟 满分:100分)
选择题(本大题共10小题,每小题3分,共30分。下列各题的备选答案中,只有一项是最符合题意的,请选出。)
1.下列四组图形中,是全等图形的一组是
A. B.
C. D.
2.如下图,已知△ABE≌△ACD,∠1=∠2,∠B=∠C,不正确的等式是
A.AB=AC B.∠BAE=∠CAD
C.BE=DC D.AD=DE
3.若△ABC≌△DEF,且△ABC的周长为20,AB=5,BC=8,则DF=
A.5 B.8
C.7 D.5或8
4.如图,△ABF≌△CDE,则
A.∠B=∠ECD B.∠A=∠ECD
C.AF=CE D.AB=CE
5.百变魔尺,魅力无穷,如图是用24段魔尺(24个等腰直角三角形,把等腰直角三角形最长边看做1)围成的长为4宽为3的长方形.用该魔尺能围出不全等的长方形个数为( )
A.3 B.4 C.5 D.6
6.如图,锐角△ABC中,D、E分别是AB、AC边上的点,△ADC≌△ADC′,△AEB≌△AEB′,且C′DEB′BC,BE、CD交于点F,若∠BAC=α,∠BFC=β,则( )
A.2α+β=180° B.2β﹣α=180° C.α+β=150° D.β﹣α=60°
7.如图,,,,则( )
A. B. C. D.
8.如图,△ABC≌△ADE,AB=AD,AC=AE,∠B=28,∠E=95,∠EAB=20,则∠BAD等于( )
A.75 B.57
C.55 D.77
9.下列命题的逆命题是真命题的是( )
A.两个全等三角形的对应角相等
B.若一个三角形的两个内角分别为和,则这个三角形是直角三角形
C.两个全等三角形的面积相等
D.如果一个数是无限不循环小数,那么这个数是无理数
10.下列命题的逆命题是真命题的是( ).
A.的平方根是3 B.是无理数
C.1的立方根是1 D.全等三角形的周长相等
填空题(本大题共5小题,每小题4分,共20分。)
11.如图,将△ABC沿BC所在的直线平移到△A'B'C'的位置,则△ABC__________△A'B'C',图中∠A与__________,∠B与__________,∠ACB与__________是对应角.
12.如图,两个三角形全等,其中已知某些边的长度和某些角的度数,则x=__________.
13.如图,,点、、、在同一条直线上,、交于点,,则的度数是______°.
14.如图,,,,,则______.
15.如图,,B、E、C、F在同一直线上,,,则CF的长为___________.
三、解答题(本大题共5小题,每小题10分,共50分。解答应写出文字说明、证明过程或演算步骤.)
16.如图,已知△ABC≌△EDC,指出其对应边和对应角.
17.在的方格纸中,每格的边长为1,请按下列要求画图.
(1)在图1中画一个格点,使与全等,且所画格点三角形的顶点均不与点B,C重合.
(2)在图2中画一个面积为7的格点四边形,且为锐角.
18.如图,已知△ABC≌△EBD,
(1)若BE=6,BD=4,求线段AD的长;
(2)若∠E=30°,∠B=48°,求∠ACE的度数.
19.如图所示,,,三点在同一直线上,且.
(1)求证:;
(2)当满足什么条件时,?
20.如图,△EFG≌△NMH,E,H,G,N在同一条直线上,EF和NM,FG和MH是对应边,若EH=1.1cm,NH=3.3cm.求线段HG的长.
参考答案
选择题
1.【答案】D
【解析】由全等形的概念可知:A、B中的两个图形大小不同,C中的形状不同,D则完全相同.故选D.
2.【答案】D
【解析】由于△ABE≌△ACD,所以对应边、对应角都相等,A、B、C三项正确,而AD和AE是相等的,所以D项是错误的.故选D.
3.【答案】C
【解析】∵△ABC的周长为20,AB=5,BC=8,∴AC=7,∵△ABC≌△DEF,∴DF=AC=7,故选C.
4.【答案】C
【解析】∵△ABF≌△CDE,∴∠B=∠D,AF=CE,AB=CD,而顶点A处不能用一个大写字母表示任何一个角,故选C.
5.【答案】A
【分析】根据14=(1+6)×2=(2+5)×2=(3+4)×2,可知能围出不全等的长方形有3个.
【详解】∵长为4、宽为3的长方形,
∴周长为2×(3+4)=14
14=(1+6)×2=(2+5)×2=(3+4)×2,
∴能围出不全等的长方形有3个,
故选:A.
6.【答案】A
【分析】延长C′D交AC于M,如图,根据全等的性质得∠C′=∠ACD,∠C′AD=∠CAD=∠B′AE=α,再利用三角形外角性质得∠C′MC=∠C′+∠C′AM=∠C′+2α,接着利用C′D∥B′E得到∠AEB=∠C′MC,而根据三角形内角和定理,三角形外角性质和等角代换,进一步变形后即可得到答案.
【详解】延长C′D交AC于M,如图,
∵△ADC≌△ADC′,△AEB≌△AEB′,
∴∠C′=∠ACD,∠C′AD=∠CAD=∠B′AE=α,
∴∠C′MC=∠C′+∠C′AM=∠C′+2α,
∵C′D∥B′E,
∴∠AEB′=∠C′MC,
∵∠AEB′=180°﹣∠B′﹣∠B′AE=180°﹣∠B′﹣α,
∴∠C′+2α=180°﹣∠B′﹣α,
∴∠C′+∠B′=180°﹣3α,
∵β=∠BFC=∠BDF+∠DBF
=∠DAC+∠ACD+∠B'
=α+∠ACD+∠B′=α+∠C′+∠B′
=α+180°﹣3α=180°﹣2α,
即:2α+β=180°.
故选:A.
7.【答案】A
【分析】根据全等三角形对应角相等即可求解;
【详解】∵ ,
∴ ∠A=∠=110°,
∵∠ABC=30°,
∴∠ACB=180°-110°-30°=40°,
故选:A.
8.【答案】D
【分析】先根据全等三角形的对应角相等得出∠B=∠D=28°,再由三角形内角和为180°,求出∠DAE=57°,然后根据∠BAD=∠DAE+∠EAB即可得出∠BAD的度数.
【详解】∵△ABC≌△ADE,
∴∠B=∠D=28°,
又∵∠D+∠E+∠DAE=180°,∠E=95°,
∴∠DAE=180°-28°-95°=57°,
∵∠EAB=20°,
∴∠BAD=∠DAE+∠EAB=77°.
故选:D.
9.【答案】D
【分析】根据原命题分别写出逆命题,然后再判断真假即可.
【详解】A、两个全等三角形的对应角相等,
逆命题是:对应角相等的两个三角形全等,是假命题;
B、若一个三角形的两个内角分别为 30° 和 60° ,则这个三角形是直角三角形,
逆命题是:如果一个三角形是直角三角形,那么它的两个内角分别为 30° 和 60° ,是假命题;
C、两个全等三角形的面积相等,
逆命题是:面积相等的两个三角形全等,是假命题;
D、如果一个数是无限不循环小数,那么这个数是无理数,
逆命题是:如果一个数是无理数,那么这个数是无限不循环小数 ,是真命题.
故选:D
10.【答案】C
【分析】根据把一个命题的条件和结论互换就得到它的逆命题,先得出逆命题,再进行判断即可.
【详解】A、的平方根是3的逆命题是:3是的平方根,是假命题;
B、是无理数的逆命题是:无理数是,是假命题;
C、1的立方根是1的逆命题是:1是1的立方根,是真命题;
D、全等三角形的周长相等的逆命题是:周长相等的三角形全等,是假命题;
故选:C.
填空题
11.【答案】≌;∠A';∠A'B'C';∠C'
【解析】∵△ABC沿BC所在的直线平移到△A'B'C'的位置,∴△ABC≌△A'B'C',∴∠A=∠A',∠B=
∠A'B'C',∠ACB=∠C',∴∠A与∠A',∠B与∠A'B'C',∠ACB与∠C'是对应角,
故答案为:≌;∠A';∠A'B'C';∠C'.
12.【答案】60°
【解析】△ABC中,∠C=180°-65°-55°=60°,根据全等三角形的对应角相等可知x=60°.故答案为:60°.
13.【答案】60
【分析】根据全等三角形的性质得到∠DFE=∠ACB=30°,根据三角形的外角性质计算,得到答案.
【详解】∵△ABC≌△DEF,
∴∠DFE=∠ACB=30°,
∵∠AMF是△MFC的一个外角,
∴∠AMF=∠DFE+∠ACB=60°,
故答案为:60.
14.【答案】3
【分析】根据全等三角形对应边相等可得AC=BD,再求出AB=CD,然后代入数据进行计算即可得解.
【详解】∵△ACE≌△DBF,
∴AC=DB,
∴AC-BC=BD-BC,
即AB=CD,
∵AD=8,BC=2,
∴AB=(AD-BC)=×(8-2)=3.
故答案为:3.
15.【答案】3
【分析】直接用全等三角形的性质可得CF=EF-CE=BC-CE,然后进行求解即可;
【详解】∵△ABC≌△DEF,
∴ BC=EF,
∵ BC=7,EC=4,
∴ CF=7-4=3,
故答案为:3.
解答题
16.【解析】∵△ABC≌△EDC,
∴AB的对应边是ED,AC的对应边是EC,BC的对应边是DC,
∠A的对应角是∠E,∠B的对应角是∠D,∠ACB的对应角是∠ECD.
17.【答案】(1)见解析;(2)见解析
【分析】(1)利用轴对称的性质解决问题即可.
(2)构造梯形,利用数形结合的思想解决问题即可.
【详解】(1)如图1中,△ADE即为所求.
(2)如图2中,四边形ABCD即为所求.
18.【答案】(1)2;(2)78°.
【分析】(1)根据△ABC≌△EBD,得AB=BE=6,根据AD=AB-BD计算即可;
(2)根据△ABC≌△EBD,得∠A=30°,利用∠ACE=∠A+∠B计算即可.
【详解】(1)∵△ABC≌△EBD,
∴AB=BE=6,
∵AD=AB-BD,BD=4,
∴AD=6-4=2;
(2)∵△ABC≌△EBD,
∴∠A=∠E=30°,
∵∠ACE=∠A+∠B,∠B=48°,
∴∠ACE=30°+48°
=78°.
19.【答案】(1)证明见解析;(2)为直角时,
【分析】(1)根据全等三角形的性质求出BD=AE,AD=CE,代入求出即可;
2)根据全等三角形的性质求出∠E=∠BDA= ,推出∠BDE= ,根据平行线的判定求出即可.
【详解】(1)证明:∵,
∴AE=BC,AC=DE,
又∵,
∴.
(2)若,则,
又∵,
∴,
∴,
又∵,
∴,
即当满足为直角时,.
20.【答案】2.2 cm
【分析】根据,可得,从而有,再计算HG的长即可.
【详解】(1),EF和NM,FG和MH是对应边,
,
,
又EH=1.1cm,NH=3.3cm,
cm,
答:线段HG的长为2.2 cm;
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
