22.2 二次函数与一元二次方程—九年级数学人教版上册课时优化训练(含解析)
文档属性
| 名称 | 22.2 二次函数与一元二次方程—九年级数学人教版上册课时优化训练(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 572.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-17 15:25:50 | ||
图片预览


文档简介
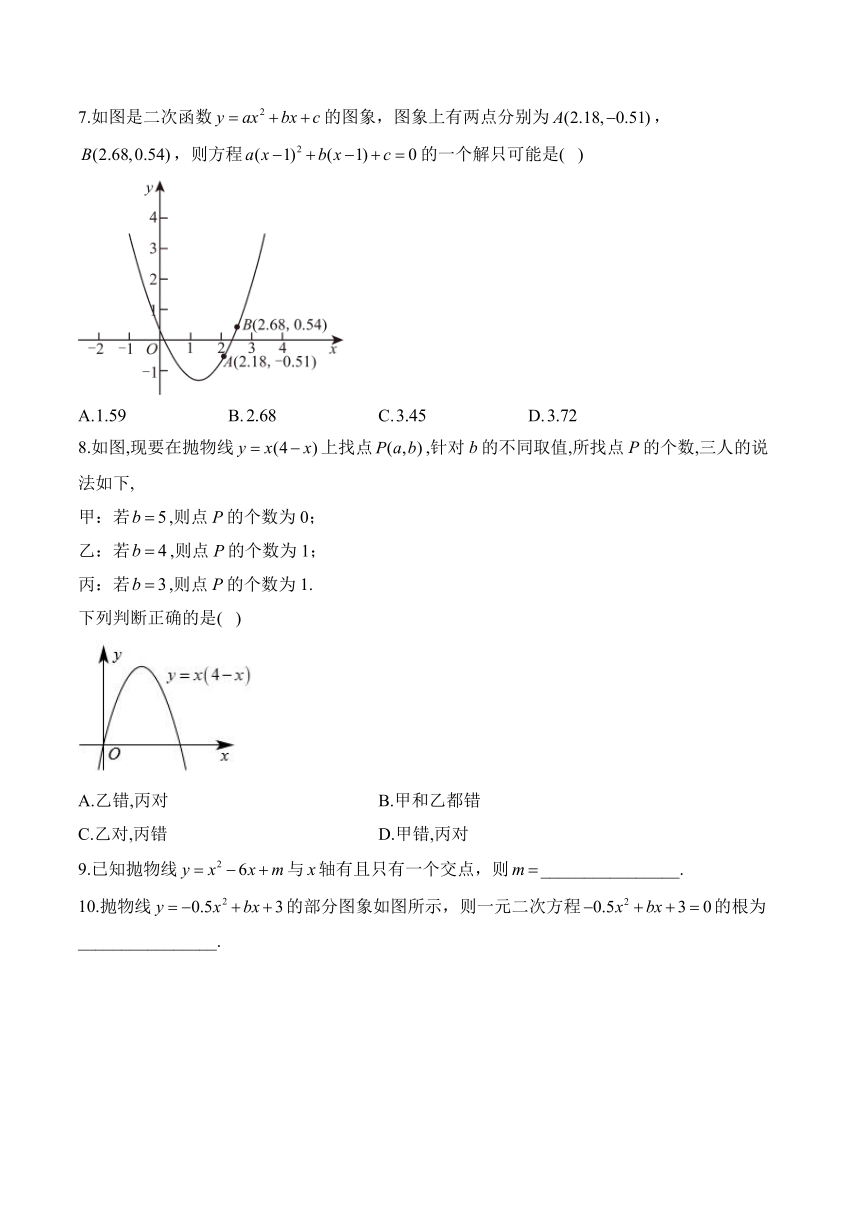
22.2 二次函数与一元二次方程—九年级数学人教版上册课时优化训练
1.图是二次函数的图象,则方程( )
A.只有一个实数根 B.有两个相等的实数根
C.有两个不相等的实数根 D.没有实数根
2.铅球运动是利用人体全身的力量,将一定重量的铅球从肩上用手臂推出的田径运动项目之一.如图,将一位运动员所推铅球的行进路线近似地看成一条抛物线,其中铅球行进高度y(m)与水平距离x(m)之间的函数关系式为,则该运动员所推铅球的水平距离为( )
A. B. C. D.
3.抛物线与坐标轴的交点个数为( )
A.0个 B.1个 C.2个 D.3个
4.若抛物线与x轴有两个不同的交点,则k的取值范围为( )
A. B. C.且 D.且
5.若关于的一元二次方程的两根分别为,,则二次函数的对称轴为直线( )
A. B. C. D.
6.一个小球以的初速度向上竖直弹出,它在空中的高度与时间满足关系式,当小球的高度为时,t为( )
A.1s B.2s C.1s或2s D.以上都不对
7.如图是二次函数的图象,图象上有两点分别为,,则方程的一个解只可能是( )
A. B. C. D.
8.如图,现要在抛物线上找点,针对b的不同取值,所找点P的个数,三人的说法如下,
甲:若,则点P的个数为0;
乙:若,则点P的个数为1;
丙:若,则点P的个数为1.
下列判断正确的是( )
A.乙错,丙对 B.甲和乙都错
C.乙对,丙错 D.甲错,丙对
9.已知抛物线与轴有且只有一个交点,则________________.
10.抛物线的部分图象如图所示,则一元二次方程的根为________________.
11.若关于x的二次函数的图象与x轴有2个公共点,则m的取值范围是______.
12.抛物线经过点、两点,则关于x的一元二次方程的解是______.
13.已知二次函数(m为常数)
(1)二次函数图像经过某定点,求出定点坐标:
(2)求证:不论m取何值,该二次函数图像与x轴总有两个交点.
14.已知的图象如图所示,根据图象回答下列问题.
(1)求方程的解;
(2)如果方程无实数根,求的取值范围.
答案以及解析
1.答案:B
解析:根据函数图象可得,二次函数与x轴只有一个交点,
方程有两个相等的实数根,
故选:B.
2.答案:A
解析:当时,
解得或,
该运动员所推铅球的水平距离为,
故选:A.
3.答案:D
解析:在中,
令,则,
,
方程有两个不相等的实数根,
时,,
抛物线与y轴的交点为,
抛物线的图象与坐标轴的交点个数为3.
故选:D.
4.答案:C
解析:∵二次函数的图象与x轴有两个交点,
∴,
∴,
∵抛物线为二次函数,
∴,
则k的取值范围为且,
故选C.
5.答案:C
解析:∵一元二次方程ax2+bx+c=0的两个根为 2和4,
∴x1+x2= =2.
∴二次函数的对称轴为x= =×2=1.
故选:C.
6.答案:C
解析:把代入,得:,
整理,得:,
因式分解,得:,
解得或.
故当秒或2秒时,小球能达到10米的高度.
故选:C.
7.答案:C
解析:二次函数图象上有两点分别为,,
方程的一个解,
方程的解为:,
即.
故选:C.
8.答案:C
解析:当时,令,整理得:,,因此点P的个数为0,甲的说法正确;
当时,令,整理得:,,因此点P有1个,乙的说法正确;
当时,令,整理得:,,因此点P有2个,丙的说法不正确;
故选:C.
9.答案:9
解析:抛物线与x轴有且只有一个交点,
方程有唯一解.
即,
解得:.
故答案为:9.
10.答案:,
解析:由图象得:抛物线与x轴的一个交点为,且对称轴为直线,
抛物线与x轴的另一个交点为,
故一元二次方程的根为:,
故答案为:,
11.答案:且
解析:关于x的二次函数的图象与x轴有2个公共点,
且,
且,
解得:且,
故答案为:且.
12.答案:,
解析:关于x的一元二次方程
变形为
因为抛物线经过点
,
所以方程的解为,
对于方程,则或,解得或,
所以一元二方程的解为,.
故答案为,.
13.答案:(1)
(2)见解析
解析:(1)
令,即,解得
即二次函数过定点
(2)将代入可得
判别式,
一元二次方程有两个不相等的实数根
则不论m取何值,该二次函数图像与x轴总有两个交点.
14.答案:(1),;
(2).
解析:(1)观察函数图象可知,图象与轴的交点坐标为,,与轴的交点坐标为,
将方程变形为,
由图象可知方程的解为,,
∴方程的解为,;
(2)若方程无实数根,
则由图象可得,
∴.
1.图是二次函数的图象,则方程( )
A.只有一个实数根 B.有两个相等的实数根
C.有两个不相等的实数根 D.没有实数根
2.铅球运动是利用人体全身的力量,将一定重量的铅球从肩上用手臂推出的田径运动项目之一.如图,将一位运动员所推铅球的行进路线近似地看成一条抛物线,其中铅球行进高度y(m)与水平距离x(m)之间的函数关系式为,则该运动员所推铅球的水平距离为( )
A. B. C. D.
3.抛物线与坐标轴的交点个数为( )
A.0个 B.1个 C.2个 D.3个
4.若抛物线与x轴有两个不同的交点,则k的取值范围为( )
A. B. C.且 D.且
5.若关于的一元二次方程的两根分别为,,则二次函数的对称轴为直线( )
A. B. C. D.
6.一个小球以的初速度向上竖直弹出,它在空中的高度与时间满足关系式,当小球的高度为时,t为( )
A.1s B.2s C.1s或2s D.以上都不对
7.如图是二次函数的图象,图象上有两点分别为,,则方程的一个解只可能是( )
A. B. C. D.
8.如图,现要在抛物线上找点,针对b的不同取值,所找点P的个数,三人的说法如下,
甲:若,则点P的个数为0;
乙:若,则点P的个数为1;
丙:若,则点P的个数为1.
下列判断正确的是( )
A.乙错,丙对 B.甲和乙都错
C.乙对,丙错 D.甲错,丙对
9.已知抛物线与轴有且只有一个交点,则________________.
10.抛物线的部分图象如图所示,则一元二次方程的根为________________.
11.若关于x的二次函数的图象与x轴有2个公共点,则m的取值范围是______.
12.抛物线经过点、两点,则关于x的一元二次方程的解是______.
13.已知二次函数(m为常数)
(1)二次函数图像经过某定点,求出定点坐标:
(2)求证:不论m取何值,该二次函数图像与x轴总有两个交点.
14.已知的图象如图所示,根据图象回答下列问题.
(1)求方程的解;
(2)如果方程无实数根,求的取值范围.
答案以及解析
1.答案:B
解析:根据函数图象可得,二次函数与x轴只有一个交点,
方程有两个相等的实数根,
故选:B.
2.答案:A
解析:当时,
解得或,
该运动员所推铅球的水平距离为,
故选:A.
3.答案:D
解析:在中,
令,则,
,
方程有两个不相等的实数根,
时,,
抛物线与y轴的交点为,
抛物线的图象与坐标轴的交点个数为3.
故选:D.
4.答案:C
解析:∵二次函数的图象与x轴有两个交点,
∴,
∴,
∵抛物线为二次函数,
∴,
则k的取值范围为且,
故选C.
5.答案:C
解析:∵一元二次方程ax2+bx+c=0的两个根为 2和4,
∴x1+x2= =2.
∴二次函数的对称轴为x= =×2=1.
故选:C.
6.答案:C
解析:把代入,得:,
整理,得:,
因式分解,得:,
解得或.
故当秒或2秒时,小球能达到10米的高度.
故选:C.
7.答案:C
解析:二次函数图象上有两点分别为,,
方程的一个解,
方程的解为:,
即.
故选:C.
8.答案:C
解析:当时,令,整理得:,,因此点P的个数为0,甲的说法正确;
当时,令,整理得:,,因此点P有1个,乙的说法正确;
当时,令,整理得:,,因此点P有2个,丙的说法不正确;
故选:C.
9.答案:9
解析:抛物线与x轴有且只有一个交点,
方程有唯一解.
即,
解得:.
故答案为:9.
10.答案:,
解析:由图象得:抛物线与x轴的一个交点为,且对称轴为直线,
抛物线与x轴的另一个交点为,
故一元二次方程的根为:,
故答案为:,
11.答案:且
解析:关于x的二次函数的图象与x轴有2个公共点,
且,
且,
解得:且,
故答案为:且.
12.答案:,
解析:关于x的一元二次方程
变形为
因为抛物线经过点
,
所以方程的解为,
对于方程,则或,解得或,
所以一元二方程的解为,.
故答案为,.
13.答案:(1)
(2)见解析
解析:(1)
令,即,解得
即二次函数过定点
(2)将代入可得
判别式,
一元二次方程有两个不相等的实数根
则不论m取何值,该二次函数图像与x轴总有两个交点.
14.答案:(1),;
(2).
解析:(1)观察函数图象可知,图象与轴的交点坐标为,,与轴的交点坐标为,
将方程变形为,
由图象可知方程的解为,,
∴方程的解为,;
(2)若方程无实数根,
则由图象可得,
∴.
同课章节目录
