22.3 实际问题与二次函数—九年级数学人教版上册课时优化训练(含解析)
文档属性
| 名称 | 22.3 实际问题与二次函数—九年级数学人教版上册课时优化训练(含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 488.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-17 15:26:20 | ||
图片预览



文档简介
22.3 实际问题与二次函数—九年级数学人教版上册课时优化训练
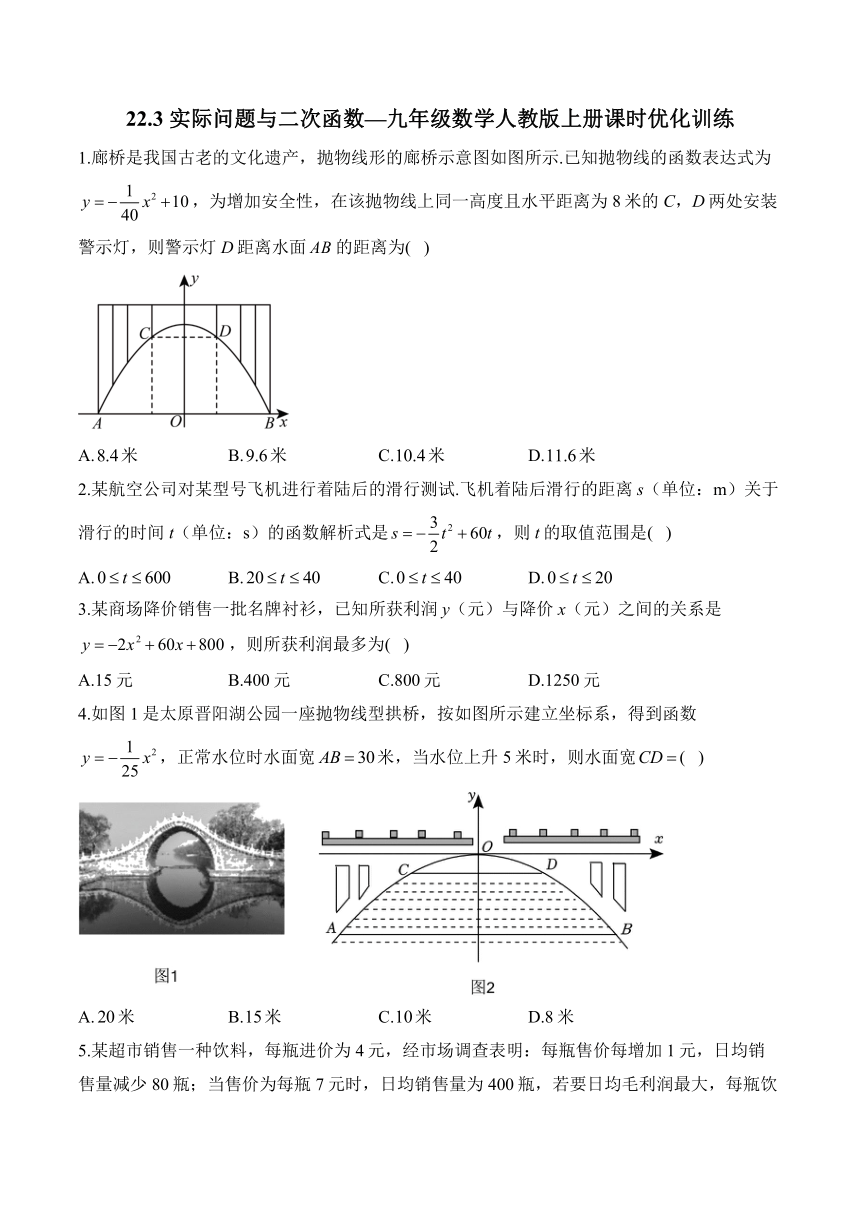
1.廊桥是我国古老的文化遗产,抛物线形的廊桥示意图如图所示.已知抛物线的函数表达式为,为增加安全性,在该抛物线上同一高度且水平距离为8米的C,D两处安装警示灯,则警示灯D距离水面的距离为( )
A.米 B.米 C.米 D.米
2.某航空公司对某型号飞机进行着陆后的滑行测试.飞机着陆后滑行的距离s(单位:m)关于滑行的时间t(单位:s)的函数解析式是,则t的取值范围是( )
A. B. C. D.
3.某商场降价销售一批名牌衬衫,已知所获利润y(元)与降价x(元)之间的关系是,则所获利润最多为( )
A.15元 B.400元 C.800元 D.1250元
4.如图1是太原晋阳湖公园一座抛物线型拱桥,按如图所示建立坐标系,得到函数,正常水位时水面宽米,当水位上升5米时,则水面宽( )
A.米 B.米 C.米 D.8米
5.某超市销售一种饮料,每瓶进价为4元,经市场调查表明:每瓶售价每增加1元,日均销售量减少80瓶;当售价为每瓶7元时,日均销售量为400瓶,若要日均毛利润最大,每瓶饮料的售价应是( )
A.6元 B.7元 C.8元 D.9元
6.用一段长度为的篱笆围成一个矩形菜地,能围成菜地的面积不可能是( ).
A. B. C. D.
7.如图,以某速度将小球沿与地面成一定角度的方向击出时,小球的飞行路线将是一条抛物线.如果不考虑空气阻力,小球在时落地,小球的飞行高度h(单位:m)与飞行时间t(单位:s)之间具有函数关系(a为常数,).有下列结论:
①a值为;
②小球的飞行高度最高可达到;
③小球有两个飞行的时间使小球的高度刚好达到.
其中,正确结论的个数是( )
A.0 B.1 C.2 D.3
8.如图所示,是一座抛物线型的拱桥,当桥下水面宽度是时,拱顶到水面的距离是,当水面下降后,水面的宽度是( )m.
A.6 B. C. D.
9.公园草坪上,自动浇水喷头喷出的水线呈一条抛物线,水线上水珠的高度y(米)关于水珠与喷头的水平距离x(米)的函数解析式是.水珠可以达到的最大高度是__________米.
10.某汽车在某速度下刹车后行驶的距离s(单位:m)与刹车后行驶的时间t(单位:s)的函数关系式为,则该汽车在该速度下从刹车后到停下来共行驶了________米.
11.东方商厦将进货单价为70元的某种商品按零售价100元一个售出时,每天能卖出20个,若这种商品的零售价在一定范围内每降价1元,其日销量就增加1个,为了获取最大利润,则应降价_________元.
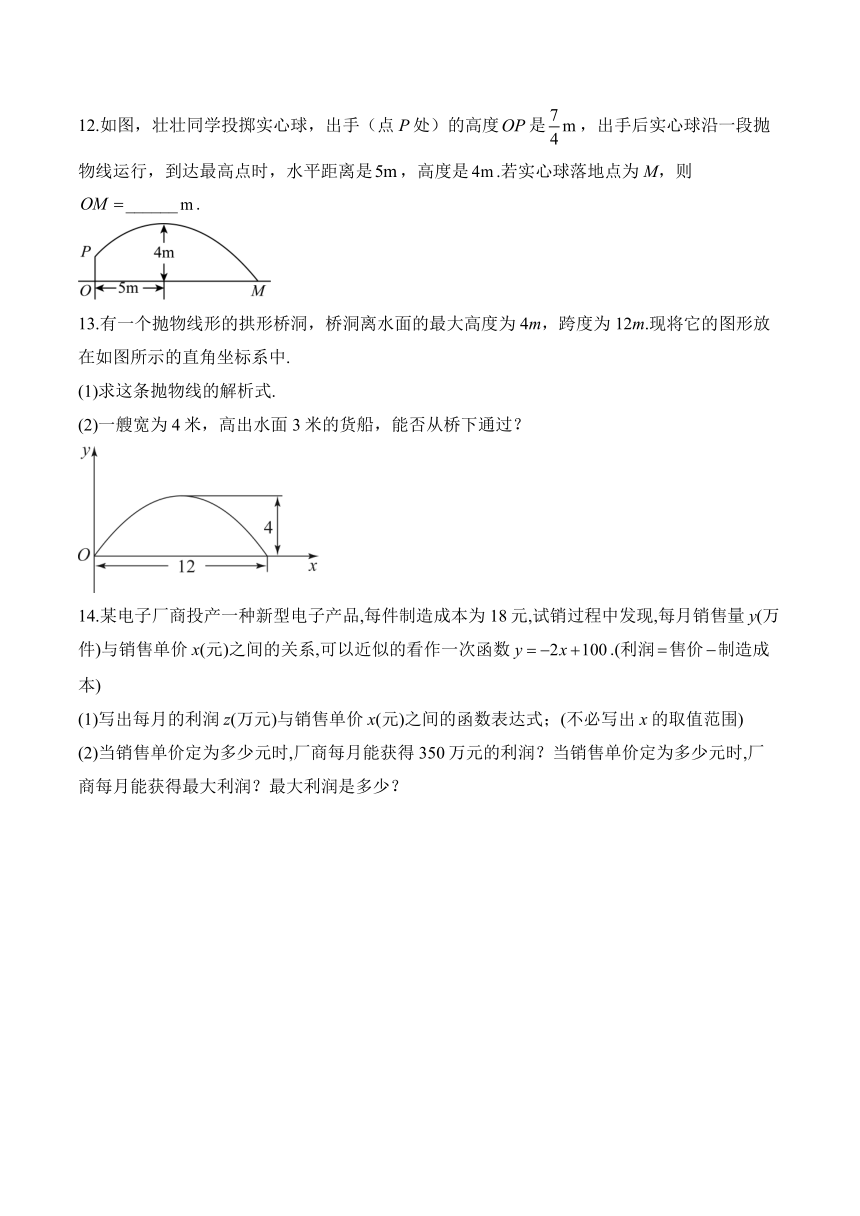
12.如图,壮壮同学投掷实心球,出手(点P处)的高度是,出手后实心球沿一段抛物线运行,到达最高点时,水平距离是,高度是.若实心球落地点为M,则______.
13.有一个抛物线形的拱形桥洞,桥洞离水面的最大高度为4m,跨度为12m.现将它的图形放在如图所示的直角坐标系中.
(1)求这条抛物线的解析式.
(2)一艘宽为4米,高出水面3米的货船,能否从桥下通过?
14.某电子厂商投产一种新型电子产品,每件制造成本为18元,试销过程中发现,每月销售量y(万件)与销售单价x(元)之间的关系,可以近似的看作一次函数.(利润售价制造成本)
(1)写出每月的利润z(万元)与销售单价x(元)之间的函数表达式;(不必写出x的取值范围)
(2)当销售单价定为多少元时,厂商每月能获得350万元的利润?当销售单价定为多少元时,厂商每月能获得最大利润?最大利润是多少?
答案以及解析
1.答案:B
解析:依题意,D的横坐标为4,
令,即,
故选B.
2.答案:D
解析:,
当s取得最大值时,飞机停下来,即,飞机停下来,
因此t的取值范围是;
故选:D.
3.答案:D
解析:,因为,所以当时,y有最大值,最大值为1250,即所获利润最多为1250元.
4.答案:A
解析:米,
当时,,
当水位上升5米时,,
把代入得,,
解得,
此时水面宽米,
故选:A.
5.答案:C
解析:设每瓶的售价为x元,日均利润为y元,由题意得;
;
;
;
当时,y有最大值;
故选:C.
6.答案:D
解析:设菜地的长为,面积为,则宽为,,
依题意得,,
,
当时,面积最大,最大值为,
,
能围成菜地的面积不可能是,
故选:D.
7.答案:C
解析:由题意得,解得,①结论正确;
函数关系,
∵,
∴小球的飞行高度最高可达到,②结论错误;
解方程,
得或,
∴小球有两个飞行的时间使小球的高度刚好达到,③结论正确.
故选:C.
8.答案:C
解析:以水面所在的直线为x轴,以这座抛物线型拱桥的对称轴为y轴,建立直角坐标系,
设抛物线的函数关系式为:,
∵抛物线过点,
∴
又∵当桥下水面宽度是时,拱顶到水面的距离是,
∴抛物线经过点,
∴,
解得
当水面下降后,
解得:,
∴水面的宽度是米,
故选:C.
9.答案:14
解析:∵,
∴时,y取最大值14,
∴水珠可以达到的最大高度是14米.
故答案为:14.
10.答案:
解析:,,
当时,s最大,
该汽车刹车后到停下来所行驶的路程为米,
故答案为:.
11.答案:5
解析:设应降价x元,每天总利润为y元,依题意:
,
,
当时,y有最大值.
故答案为5.
12.答案:
解析:以点O为坐标原点,射线方向为x轴正半轴,射线方向为y轴正半轴,建立平面直角坐标系,
出手后实心球沿一段抛物线运行,到达最高点时,水平距离是,高度是.
设抛物线解析式为:,
把点代入得:,
解得:,
抛物线解析式为:;
当时,,
解得,(舍去),,
即此次实心球被推出的水平距离为.
故答案为:.
13.答案:(1)
(2)一艘宽为4米,高出水面3米的货船,能从桥下通过,理由见解析.
解析:(1)根据题意抛物线经过了原点,设抛物线为:
把代入抛物线的解析式得:
解得:
所以抛物线为:
(2)因为一艘宽为4米,高出水面3米的货船行驶时航线在正中间,
所以当时,
而
所以一艘宽为4米,高出水面3米的货船,能从桥下通过.
14.答案:(1)
(2)25元或43元;34元,512万元
解析:(1)由题意得,
;
故答案为:;
(2)当时,
,
解得:,.
答:当销售单价为25元或43元时,厂商每月获得的利润为350万元.
,
当销售单价定为34元时,厂商每月能获得最大利润,最大利润是512万元.
1.廊桥是我国古老的文化遗产,抛物线形的廊桥示意图如图所示.已知抛物线的函数表达式为,为增加安全性,在该抛物线上同一高度且水平距离为8米的C,D两处安装警示灯,则警示灯D距离水面的距离为( )
A.米 B.米 C.米 D.米
2.某航空公司对某型号飞机进行着陆后的滑行测试.飞机着陆后滑行的距离s(单位:m)关于滑行的时间t(单位:s)的函数解析式是,则t的取值范围是( )
A. B. C. D.
3.某商场降价销售一批名牌衬衫,已知所获利润y(元)与降价x(元)之间的关系是,则所获利润最多为( )
A.15元 B.400元 C.800元 D.1250元
4.如图1是太原晋阳湖公园一座抛物线型拱桥,按如图所示建立坐标系,得到函数,正常水位时水面宽米,当水位上升5米时,则水面宽( )
A.米 B.米 C.米 D.8米
5.某超市销售一种饮料,每瓶进价为4元,经市场调查表明:每瓶售价每增加1元,日均销售量减少80瓶;当售价为每瓶7元时,日均销售量为400瓶,若要日均毛利润最大,每瓶饮料的售价应是( )
A.6元 B.7元 C.8元 D.9元
6.用一段长度为的篱笆围成一个矩形菜地,能围成菜地的面积不可能是( ).
A. B. C. D.
7.如图,以某速度将小球沿与地面成一定角度的方向击出时,小球的飞行路线将是一条抛物线.如果不考虑空气阻力,小球在时落地,小球的飞行高度h(单位:m)与飞行时间t(单位:s)之间具有函数关系(a为常数,).有下列结论:
①a值为;
②小球的飞行高度最高可达到;
③小球有两个飞行的时间使小球的高度刚好达到.
其中,正确结论的个数是( )
A.0 B.1 C.2 D.3
8.如图所示,是一座抛物线型的拱桥,当桥下水面宽度是时,拱顶到水面的距离是,当水面下降后,水面的宽度是( )m.
A.6 B. C. D.
9.公园草坪上,自动浇水喷头喷出的水线呈一条抛物线,水线上水珠的高度y(米)关于水珠与喷头的水平距离x(米)的函数解析式是.水珠可以达到的最大高度是__________米.
10.某汽车在某速度下刹车后行驶的距离s(单位:m)与刹车后行驶的时间t(单位:s)的函数关系式为,则该汽车在该速度下从刹车后到停下来共行驶了________米.
11.东方商厦将进货单价为70元的某种商品按零售价100元一个售出时,每天能卖出20个,若这种商品的零售价在一定范围内每降价1元,其日销量就增加1个,为了获取最大利润,则应降价_________元.
12.如图,壮壮同学投掷实心球,出手(点P处)的高度是,出手后实心球沿一段抛物线运行,到达最高点时,水平距离是,高度是.若实心球落地点为M,则______.
13.有一个抛物线形的拱形桥洞,桥洞离水面的最大高度为4m,跨度为12m.现将它的图形放在如图所示的直角坐标系中.
(1)求这条抛物线的解析式.
(2)一艘宽为4米,高出水面3米的货船,能否从桥下通过?
14.某电子厂商投产一种新型电子产品,每件制造成本为18元,试销过程中发现,每月销售量y(万件)与销售单价x(元)之间的关系,可以近似的看作一次函数.(利润售价制造成本)
(1)写出每月的利润z(万元)与销售单价x(元)之间的函数表达式;(不必写出x的取值范围)
(2)当销售单价定为多少元时,厂商每月能获得350万元的利润?当销售单价定为多少元时,厂商每月能获得最大利润?最大利润是多少?
答案以及解析
1.答案:B
解析:依题意,D的横坐标为4,
令,即,
故选B.
2.答案:D
解析:,
当s取得最大值时,飞机停下来,即,飞机停下来,
因此t的取值范围是;
故选:D.
3.答案:D
解析:,因为,所以当时,y有最大值,最大值为1250,即所获利润最多为1250元.
4.答案:A
解析:米,
当时,,
当水位上升5米时,,
把代入得,,
解得,
此时水面宽米,
故选:A.
5.答案:C
解析:设每瓶的售价为x元,日均利润为y元,由题意得;
;
;
;
当时,y有最大值;
故选:C.
6.答案:D
解析:设菜地的长为,面积为,则宽为,,
依题意得,,
,
当时,面积最大,最大值为,
,
能围成菜地的面积不可能是,
故选:D.
7.答案:C
解析:由题意得,解得,①结论正确;
函数关系,
∵,
∴小球的飞行高度最高可达到,②结论错误;
解方程,
得或,
∴小球有两个飞行的时间使小球的高度刚好达到,③结论正确.
故选:C.
8.答案:C
解析:以水面所在的直线为x轴,以这座抛物线型拱桥的对称轴为y轴,建立直角坐标系,
设抛物线的函数关系式为:,
∵抛物线过点,
∴
又∵当桥下水面宽度是时,拱顶到水面的距离是,
∴抛物线经过点,
∴,
解得
当水面下降后,
解得:,
∴水面的宽度是米,
故选:C.
9.答案:14
解析:∵,
∴时,y取最大值14,
∴水珠可以达到的最大高度是14米.
故答案为:14.
10.答案:
解析:,,
当时,s最大,
该汽车刹车后到停下来所行驶的路程为米,
故答案为:.
11.答案:5
解析:设应降价x元,每天总利润为y元,依题意:
,
,
当时,y有最大值.
故答案为5.
12.答案:
解析:以点O为坐标原点,射线方向为x轴正半轴,射线方向为y轴正半轴,建立平面直角坐标系,
出手后实心球沿一段抛物线运行,到达最高点时,水平距离是,高度是.
设抛物线解析式为:,
把点代入得:,
解得:,
抛物线解析式为:;
当时,,
解得,(舍去),,
即此次实心球被推出的水平距离为.
故答案为:.
13.答案:(1)
(2)一艘宽为4米,高出水面3米的货船,能从桥下通过,理由见解析.
解析:(1)根据题意抛物线经过了原点,设抛物线为:
把代入抛物线的解析式得:
解得:
所以抛物线为:
(2)因为一艘宽为4米,高出水面3米的货船行驶时航线在正中间,
所以当时,
而
所以一艘宽为4米,高出水面3米的货船,能从桥下通过.
14.答案:(1)
(2)25元或43元;34元,512万元
解析:(1)由题意得,
;
故答案为:;
(2)当时,
,
解得:,.
答:当销售单价为25元或43元时,厂商每月获得的利润为350万元.
,
当销售单价定为34元时,厂商每月能获得最大利润,最大利润是512万元.
同课章节目录
