24.2.2 直线与圆的位置关系
文档属性
| 名称 | 24.2.2 直线与圆的位置关系 |  | |
| 格式 | rar | ||
| 文件大小 | 736.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-10-05 15:20:00 | ||
图片预览



文档简介
课件18张PPT。24.2.2 直线和圆的位置关系南门学校 九年(1)(2)班直线和圆的位置有
何关系???图 1b.A.O图 2c.
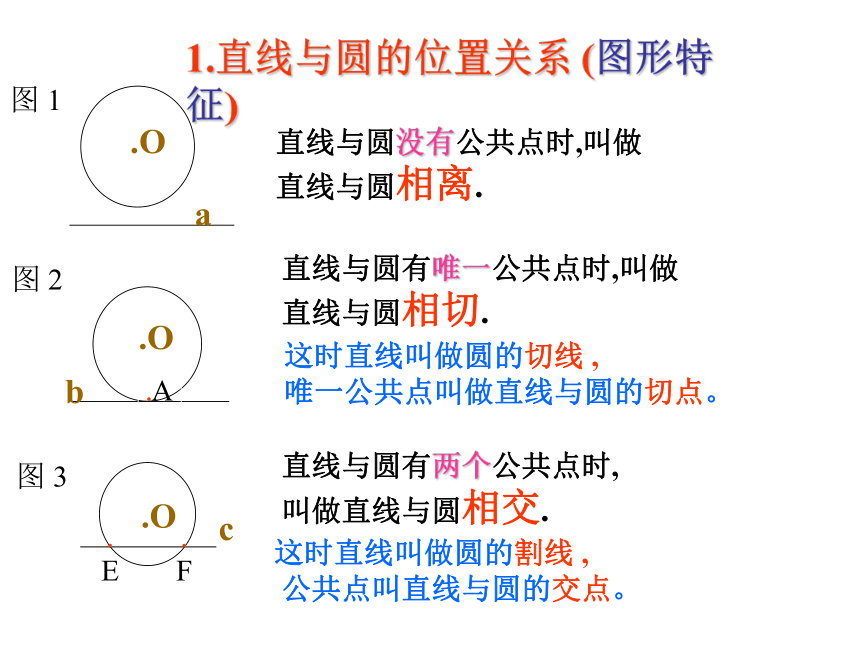
F.E.O图 3这时直线叫做圆的割线 ,
公共点叫直线与圆的交点。直线与圆没有公共点时,叫做直线与圆相离.直线与圆有唯一公共点时,叫做直线与圆相切.直线与圆有两个公共点时,叫做直线与圆相交. 这时直线叫做圆的切线 ,
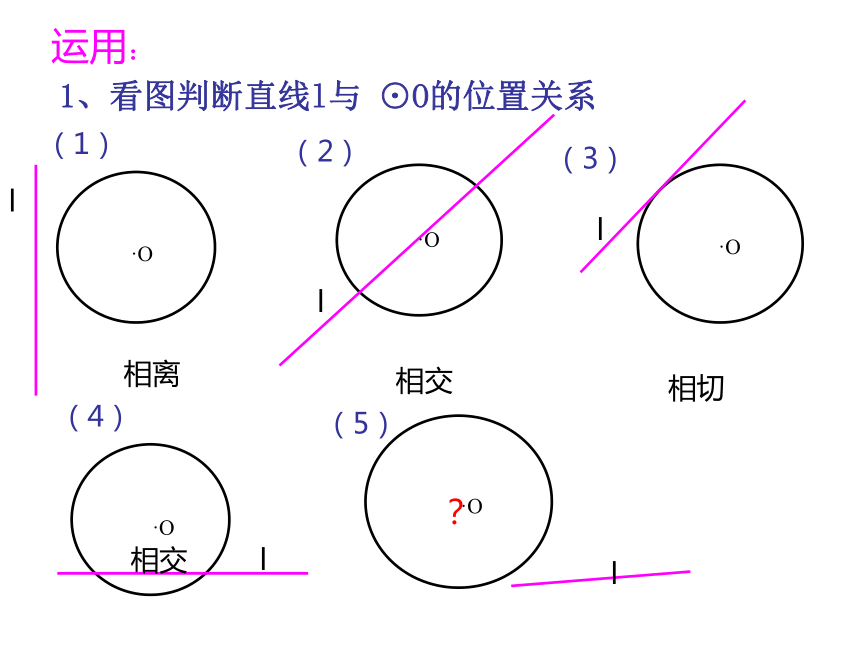
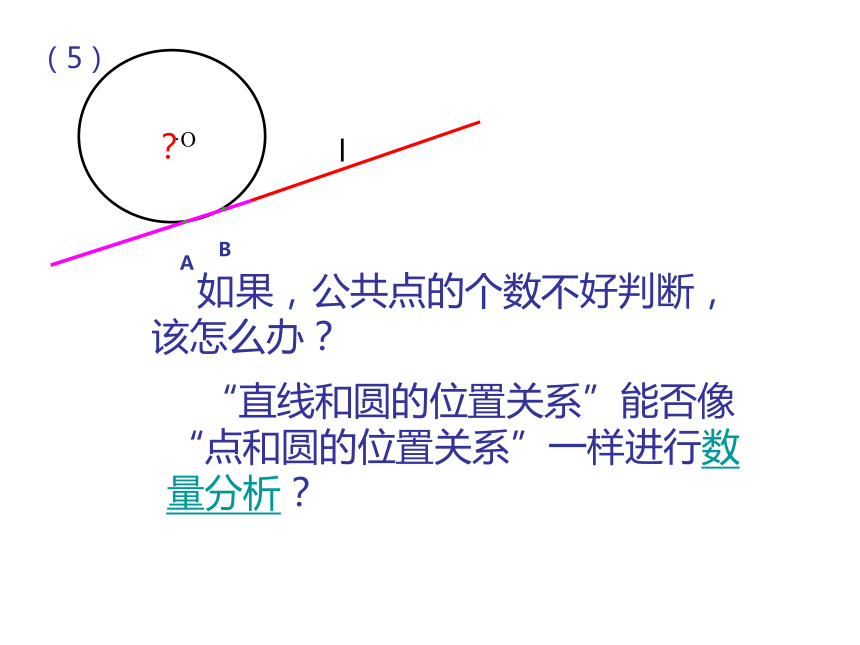
唯一公共点叫做直线与圆的切点。1.直线与圆的位置关系 (图形特征)运用:1、看图判断直线l与 ⊙O的位置关系(1)(2)(3)(4)(5)相离相切相交相交?lllll·O·O·O·O·O(5)?l 如果,公共点的个数不好判断,该怎么办?·O “直线和圆的位置关系”能否像“点和圆的位置关系”一样进行数量分析?·
A·
Bddd.O.O.Orrr相离相切相交看一看想一想lll.A.B.
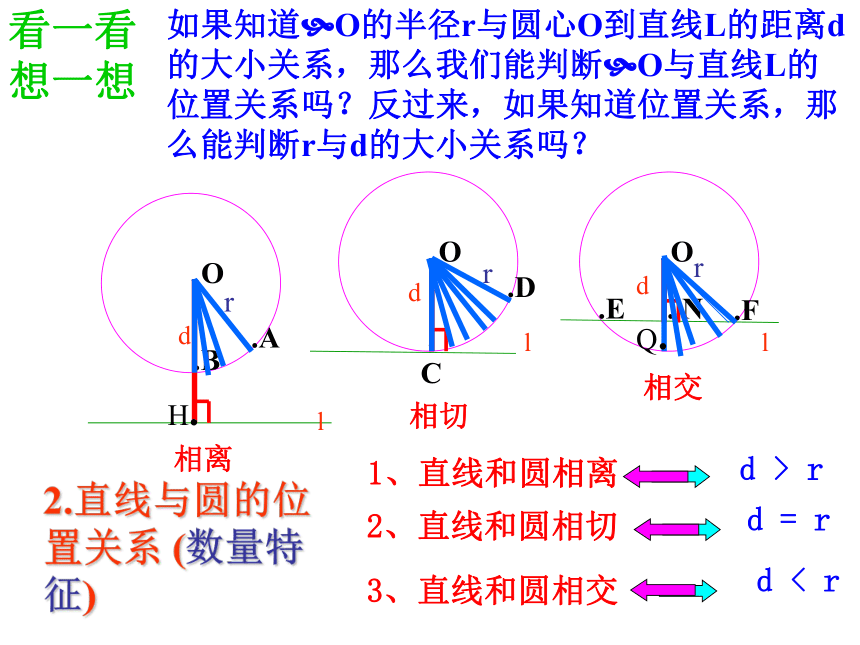
C.D.E.F. NH.Q.如果知道?O的半径r与圆心O到直线L的距离d的大小关系,那么我们能判断?O与直线L的位置关系吗?反过来,如果知道位置关系,那么能判断r与d的大小关系吗?1、直线和圆相离d > r2、直线和圆相切d = r3、直线和圆相交d < r2.直线与圆的位置关系 (数量特征)例1:填空:1、已知⊙O的半径为5cm,点O到直线a的距离
为3cm,则⊙O与直线a的位置关系是_____;
直线a与⊙O的公共点个数是____.相交 相切两个3、已知⊙O的直径为10cm,点O到直线a的距离
为7cm,则⊙O与直线a的位置关系是 ___ _;
直线a与⊙O的公共点个数是____。零相离一个小结:利用圆心到直线的距离与半径的大小关
系来识别直线与圆的位置关系2、已知⊙O的直径是11cm,点O到直线a的距离
是5.5cm,则⊙O与直线a的位置关系是 ___ _;
直线a与⊙O的公共点个数是____.4、直线m上一点A到圆心O的距离等于⊙O的半径,
则直线m与⊙O的位置关系是 。相切 或相交例题2:分析在Rt△ABC中,∠C=90°,AC=3cm,BC=4cm,以C为圆心,r为半径的圆
与AB有怎样的位置关系?为什么?
(1)r=2cm;(2)r=2.4cm (3)r=3cm。BCAD4532.4cm即圆心C到AB的距离d=2.4cm。(1)当r=2cm时, ∵d>r,
∴⊙C与AB相离。(2)当r=2.4cm时,∵d=r,
∴⊙C与AB相切。(3)当r=3cm时, ∵d<r,
∴⊙C与AB相交。解:过C作CD⊥AB,垂足为D。在Rt△ABC中,AB= ==5(cm)根据三角形面积公式有CD·AB=AC·BC∴CD= =2222=2.4(cm)。ABCAD453d=2.4例: Rt△ABC,∠C=90°AC=3cm,BC=4cm,以C为圆心,r为半径的圆与AB有怎样的位置关系?为什么?
(1)r=2cm;(2)r=2.4cm
(3)r=3cm。1、当r满足________________时,⊙C与直线AB相离。2、当r满足____________ 时,⊙C与直线AB相切。3、当r满足____________时,
⊙C与直线AB相交。BCAD45d=2.4cm30cmBC=4cm,以C为圆心,r为半径作圆。在Rt△ABC中,∠C=90°,
AC=3cm,BC=4cm,
以C为圆心,r为半径作圆。想一想?4.当r满足___________
_____________ 时,⊙C与线段AB只有一个公共点. r=2.4cmBCAD453d=2.4cm 或3cmOABM课堂练习2.如图,已知∠AOB=β(β为锐角) ,M为OB上一点,OM=5cm,以M为圆心、以2.5为半径作圆
(1)⊙M与直线OA的位置关系由 大小决定.
(2)若⊙M与直线OA相切,则β=
(3)若⊙M与直线OA相交,则β的取值范围是β30°0°≤β≤30°β0°≤β<30° 1.若⊙O与直线m的距离为d,⊙O 的半径为r,若d,r 的两个根,则直线m与⊙O的位置若d,r是方程与⊙O的位置关系是相切,则a的值是 。关系是 。小结:0d>r1d=r切点切线2d二 直线和圆位置关系的性质与判定
( r与d的数量大小关系)(性质)(判定)相切
相交
1.:如图,正三角形ABC的边长为6 厘米,⊙O的半径为r厘米,当圆心O从点A出发,沿着线路AB一BC一CA运动,回到点A时,⊙O随着点O的运动而移动.在⊙O移动过程中,从切点的个数来考虑,相切有几种不同的情况?写出不同情况下,r的取值范围及相应的切点个数.ABC2.如图:菱形ABCD的边长为5cm,∠B=60°当以A为圆心的圆与BC相切时,半径是 ,此时⊙A与CD的位置关系是 。3.如图,一热带风暴中心O距A岛为2千米,风暴影响圈的半径为1千米.有一条船从A岛出发沿AB方向航行,问∠BAO的度数是多少时船就会进入风暴影响圈?4.如图,在直角梯形ABCD中,∠B=90°,AD∥BC, ∠C= 30° ,AD=1,AB=2.
试猜想在BC是否存在一点P,使得⊙P与线段CD、
AB都相切,如存在,请确定⊙P的半径. 挑战自我!再见
何关系???图 1b.A.O图 2c.
F.E.O图 3这时直线叫做圆的割线 ,
公共点叫直线与圆的交点。直线与圆没有公共点时,叫做直线与圆相离.直线与圆有唯一公共点时,叫做直线与圆相切.直线与圆有两个公共点时,叫做直线与圆相交. 这时直线叫做圆的切线 ,
唯一公共点叫做直线与圆的切点。1.直线与圆的位置关系 (图形特征)运用:1、看图判断直线l与 ⊙O的位置关系(1)(2)(3)(4)(5)相离相切相交相交?lllll·O·O·O·O·O(5)?l 如果,公共点的个数不好判断,该怎么办?·O “直线和圆的位置关系”能否像“点和圆的位置关系”一样进行数量分析?·
A·
Bddd.O.O.Orrr相离相切相交看一看想一想lll.A.B.
C.D.E.F. NH.Q.如果知道?O的半径r与圆心O到直线L的距离d的大小关系,那么我们能判断?O与直线L的位置关系吗?反过来,如果知道位置关系,那么能判断r与d的大小关系吗?1、直线和圆相离d > r2、直线和圆相切d = r3、直线和圆相交d < r2.直线与圆的位置关系 (数量特征)例1:填空:1、已知⊙O的半径为5cm,点O到直线a的距离
为3cm,则⊙O与直线a的位置关系是_____;
直线a与⊙O的公共点个数是____.相交 相切两个3、已知⊙O的直径为10cm,点O到直线a的距离
为7cm,则⊙O与直线a的位置关系是 ___ _;
直线a与⊙O的公共点个数是____。零相离一个小结:利用圆心到直线的距离与半径的大小关
系来识别直线与圆的位置关系2、已知⊙O的直径是11cm,点O到直线a的距离
是5.5cm,则⊙O与直线a的位置关系是 ___ _;
直线a与⊙O的公共点个数是____.4、直线m上一点A到圆心O的距离等于⊙O的半径,
则直线m与⊙O的位置关系是 。相切 或相交例题2:分析在Rt△ABC中,∠C=90°,AC=3cm,BC=4cm,以C为圆心,r为半径的圆
与AB有怎样的位置关系?为什么?
(1)r=2cm;(2)r=2.4cm (3)r=3cm。BCAD4532.4cm即圆心C到AB的距离d=2.4cm。(1)当r=2cm时, ∵d>r,
∴⊙C与AB相离。(2)当r=2.4cm时,∵d=r,
∴⊙C与AB相切。(3)当r=3cm时, ∵d<r,
∴⊙C与AB相交。解:过C作CD⊥AB,垂足为D。在Rt△ABC中,AB= ==5(cm)根据三角形面积公式有CD·AB=AC·BC∴CD= =2222=2.4(cm)。ABCAD453d=2.4例: Rt△ABC,∠C=90°AC=3cm,BC=4cm,以C为圆心,r为半径的圆与AB有怎样的位置关系?为什么?
(1)r=2cm;(2)r=2.4cm
(3)r=3cm。1、当r满足________________时,⊙C与直线AB相离。2、当r满足____________ 时,⊙C与直线AB相切。3、当r满足____________时,
⊙C与直线AB相交。BCAD45d=2.4cm30cm
AC=3cm,BC=4cm,
以C为圆心,r为半径作圆。想一想?4.当r满足___________
_____________ 时,⊙C与线段AB只有一个公共点. r=2.4cmBCAD453d=2.4cm 或3cm
(1)⊙M与直线OA的位置关系由 大小决定.
(2)若⊙M与直线OA相切,则β=
(3)若⊙M与直线OA相交,则β的取值范围是β30°0°≤β≤30°β0°≤β<30° 1.若⊙O与直线m的距离为d,⊙O 的半径为r,若d,r 的两个根,则直线m与⊙O的位置若d,r是方程与⊙O的位置关系是相切,则a的值是 。关系是 。小结:0d>r1d=r切点切线2d
( r与d的数量大小关系)(性质)(判定)相切
相交
1.:如图,正三角形ABC的边长为6 厘米,⊙O的半径为r厘米,当圆心O从点A出发,沿着线路AB一BC一CA运动,回到点A时,⊙O随着点O的运动而移动.在⊙O移动过程中,从切点的个数来考虑,相切有几种不同的情况?写出不同情况下,r的取值范围及相应的切点个数.ABC2.如图:菱形ABCD的边长为5cm,∠B=60°当以A为圆心的圆与BC相切时,半径是 ,此时⊙A与CD的位置关系是 。3.如图,一热带风暴中心O距A岛为2千米,风暴影响圈的半径为1千米.有一条船从A岛出发沿AB方向航行,问∠BAO的度数是多少时船就会进入风暴影响圈?4.如图,在直角梯形ABCD中,∠B=90°,AD∥BC, ∠C= 30° ,AD=1,AB=2.
试猜想在BC是否存在一点P,使得⊙P与线段CD、
AB都相切,如存在,请确定⊙P的半径. 挑战自我!再见
同课章节目录
