第二章 轴对称 3 简单的轴对称图形 第3 课时 等腰三角形的性质
文档属性
| 名称 | 第二章 轴对称 3 简单的轴对称图形 第3 课时 等腰三角形的性质 |

|
|
| 格式 | docx | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-17 00:00:00 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
第二章 轴对称
3 简单的轴对称图形
第3 课时 等腰三角形的性质
列清单·划重点
知识点① 等腰三角形的性质
1.等腰三角形是____________图形.
2.等腰三角形顶角的________、底边上的________、底边上的________互相重合(也称“三线合一”),它们所在的_________都是等腰三角形的对称轴.
3.等腰三角形的两个__________相等.
知识点② 等边三角形的性质
1.边:三边____________,每边上“三线合一”.
2.角:三个角都是____________.
3.对称性:等边三角形是____________图形,有____________条对称轴.
明考点·识方法
考点① 等腰三角形的性质
典例 1 如图所示,在△ABC中,AB=AC,AD⊥BC 于点 D,若 AB=6,CD=4,则△ABC的周长是___________.
思路导析 因为 AB=AC,AD⊥BC 于点 D,CD=4,所以 BD=CD=4,又因为AB=6,所以 △ABC的周长为AB+AC+BD+CD=6+6+4+4=20.
变式1 等腰三角形的一个内角为70°,则另外两个内角的度数分别是 ( )
A.55°,55° B.70°,40°或70°,55°
C.70°,40° D.55°,55°或70°,40°
变式2 如图所示,在△ABC中,AB=AC,点 D 为BC 的中点,∠BAD=20°,则∠C 的度数是 ( )
考点② 等边三角形的性质 典例微课
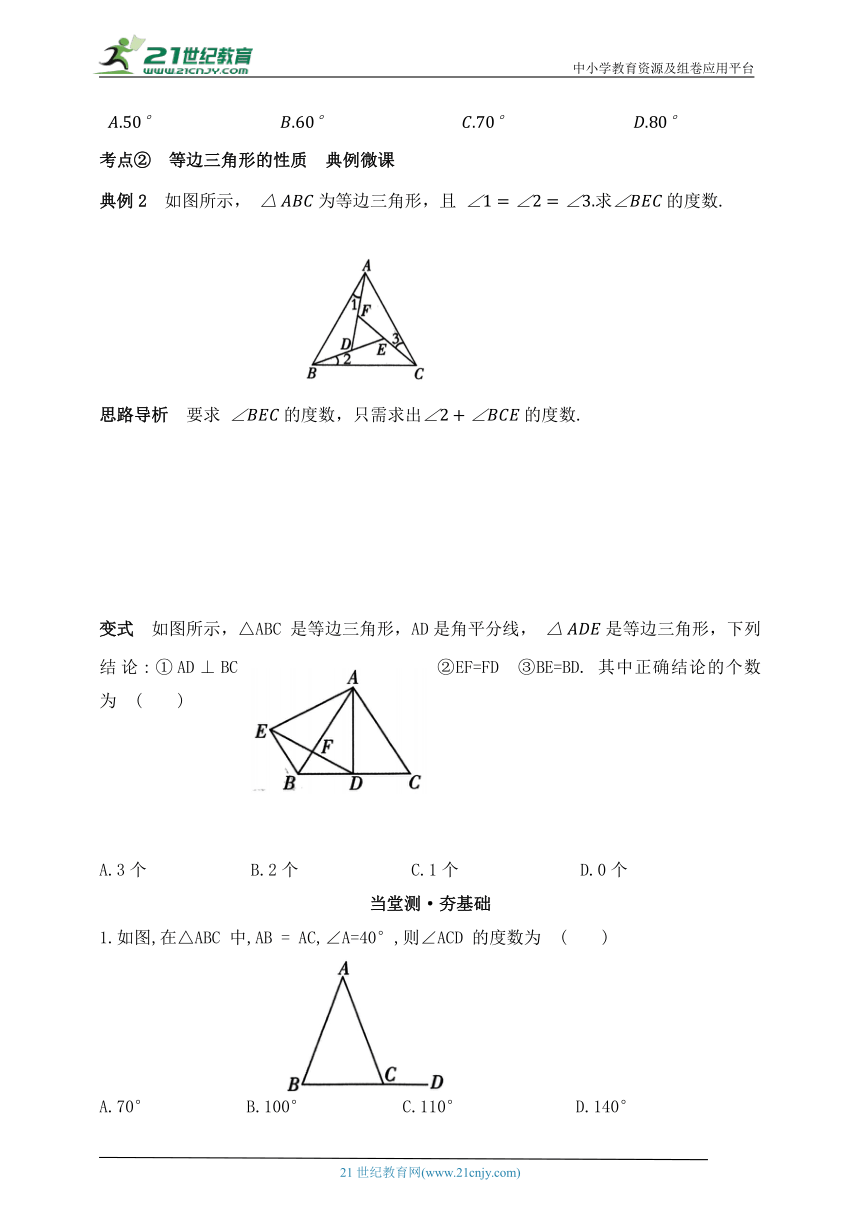
典例2 如图所示, 为等边三角形,且 求的度数.
思路导析 要求 的度数,只需求出的度数.
变式 如图所示,△ABC 是等边三角形,AD是角平分线, 是等边三角形,下列结论:①AD⊥BC ②EF=FD ③BE=BD. 其中正确结论的个数为 ( )
A.3个 B.2个 C.1个 D.0个
当堂测·夯基础
1.如图,在△ABC 中,AB = AC,∠A=40°,则∠ACD 的度数为 ( )
A.70° B.100° C.110° D.140°
2.一个等腰三角形一边长为 4 cm,另一边长为 5 cm ,那么这个等腰三角形的周长是 ( )
A.13 cm B.14 cm C.13 cm或 14 cm D.以上都不对
3.如图所示,在等边△ABC中,点 D,E 分别在边 BC,AB上,且 BD=AE,AD与CE 交于点 F,则∠FDC+∠FCD的度数为 ( )
A.60° B.120° C.110° D.135°
第3题图 第4题图
4.如图所示,在等边△ABC中,点 E 为AB 上一点,且 DE⊥AC,则∠AED=___________.
5.如图,在等边△ABC中,点 D 是 AC 边上一点,点 E是BC 延长线上一点,连接 BD,DE,若∠ABD= 20°, BD= DE. 求∠CDE 的度数.
参考答案
【列清单·划重点】
知识点1
1.轴对称
2.平分线 中线 高 直线
3.底角
知识点2
1.相等 2.60° 3.轴对称 三
【明考点·识方法】
典例 1 20 变式 1 D 变式2 C
典例2 解:因为△ABC为等边三角形,所以∠BAC=∠ABC=∠ACB=60°.
又因为∠2=∠3,所以∠2+∠BCE=∠3+∠BCE=∠ACB=60°.
在△BEC中,∠2+∠BCE+∠BEC=180°,所以∠BEC=180°-60°=120°.
变式 A
【当堂测·夯基础】
1. C 2. C 3. B 4.30°
5.解:因为△ABC是等边三角形,所以∠ABC=∠ACB=60°,
因为∠ABD=20°,所以∠DBC=∠ABC=∠ABD=40°.
因为 BD=DE,所以∠DBC=∠E=40°.
因为∠ACB=60°,所以∠ACE=120°,
所以∠CDE=180°-∠ACE-∠E=180°-120°-40°=20°,
所以∠CDE的度数为20°.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第二章 轴对称
3 简单的轴对称图形
第3 课时 等腰三角形的性质
列清单·划重点
知识点① 等腰三角形的性质
1.等腰三角形是____________图形.
2.等腰三角形顶角的________、底边上的________、底边上的________互相重合(也称“三线合一”),它们所在的_________都是等腰三角形的对称轴.
3.等腰三角形的两个__________相等.
知识点② 等边三角形的性质
1.边:三边____________,每边上“三线合一”.
2.角:三个角都是____________.
3.对称性:等边三角形是____________图形,有____________条对称轴.
明考点·识方法
考点① 等腰三角形的性质
典例 1 如图所示,在△ABC中,AB=AC,AD⊥BC 于点 D,若 AB=6,CD=4,则△ABC的周长是___________.
思路导析 因为 AB=AC,AD⊥BC 于点 D,CD=4,所以 BD=CD=4,又因为AB=6,所以 △ABC的周长为AB+AC+BD+CD=6+6+4+4=20.
变式1 等腰三角形的一个内角为70°,则另外两个内角的度数分别是 ( )
A.55°,55° B.70°,40°或70°,55°
C.70°,40° D.55°,55°或70°,40°
变式2 如图所示,在△ABC中,AB=AC,点 D 为BC 的中点,∠BAD=20°,则∠C 的度数是 ( )
考点② 等边三角形的性质 典例微课
典例2 如图所示, 为等边三角形,且 求的度数.
思路导析 要求 的度数,只需求出的度数.
变式 如图所示,△ABC 是等边三角形,AD是角平分线, 是等边三角形,下列结论:①AD⊥BC ②EF=FD ③BE=BD. 其中正确结论的个数为 ( )
A.3个 B.2个 C.1个 D.0个
当堂测·夯基础
1.如图,在△ABC 中,AB = AC,∠A=40°,则∠ACD 的度数为 ( )
A.70° B.100° C.110° D.140°
2.一个等腰三角形一边长为 4 cm,另一边长为 5 cm ,那么这个等腰三角形的周长是 ( )
A.13 cm B.14 cm C.13 cm或 14 cm D.以上都不对
3.如图所示,在等边△ABC中,点 D,E 分别在边 BC,AB上,且 BD=AE,AD与CE 交于点 F,则∠FDC+∠FCD的度数为 ( )
A.60° B.120° C.110° D.135°
第3题图 第4题图
4.如图所示,在等边△ABC中,点 E 为AB 上一点,且 DE⊥AC,则∠AED=___________.
5.如图,在等边△ABC中,点 D 是 AC 边上一点,点 E是BC 延长线上一点,连接 BD,DE,若∠ABD= 20°, BD= DE. 求∠CDE 的度数.
参考答案
【列清单·划重点】
知识点1
1.轴对称
2.平分线 中线 高 直线
3.底角
知识点2
1.相等 2.60° 3.轴对称 三
【明考点·识方法】
典例 1 20 变式 1 D 变式2 C
典例2 解:因为△ABC为等边三角形,所以∠BAC=∠ABC=∠ACB=60°.
又因为∠2=∠3,所以∠2+∠BCE=∠3+∠BCE=∠ACB=60°.
在△BEC中,∠2+∠BCE+∠BEC=180°,所以∠BEC=180°-60°=120°.
变式 A
【当堂测·夯基础】
1. C 2. C 3. B 4.30°
5.解:因为△ABC是等边三角形,所以∠ABC=∠ACB=60°,
因为∠ABD=20°,所以∠DBC=∠ABC=∠ABD=40°.
因为 BD=DE,所以∠DBC=∠E=40°.
因为∠ACB=60°,所以∠ACE=120°,
所以∠CDE=180°-∠ACE-∠E=180°-120°-40°=20°,
所以∠CDE的度数为20°.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
