人教版数学八年级上册13.1.1轴对称 精品同步练习(含解析)
文档属性
| 名称 | 人教版数学八年级上册13.1.1轴对称 精品同步练习(含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-17 13:52:31 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
人教版八年级上册数学 13.1.1轴对称 同步练习
(考试时间:60分钟 满分:100分)
选择题(本大题共10小题,每小题3分,共30分。下列各题的备选答案中,只有一项是最符合题意的,请选出。)
1.下列字母中:H、F、A、O、M、W、Y、E,轴对称图形的个数是()
A.5 B.4 C.6 D.7
2.等腰三角形、直角三角形、等边三角形、锐角三角形、钝角三角形和等腰直角三角形中,一定是轴对称图形的有()
A.3个 B.4个 C.5个 D.2个
3.下列图案中,不能用折叠剪纸方法得到的是()
A. B. C. D.
4.下列四个图形分别是节能、节水、绿色食品和低碳标志,其中轴对称图形是( )
A. B. C. D.
5.如图,在中,,将沿直线翻折,点落在点的位置,则的度数是( )
A. B. C. D.
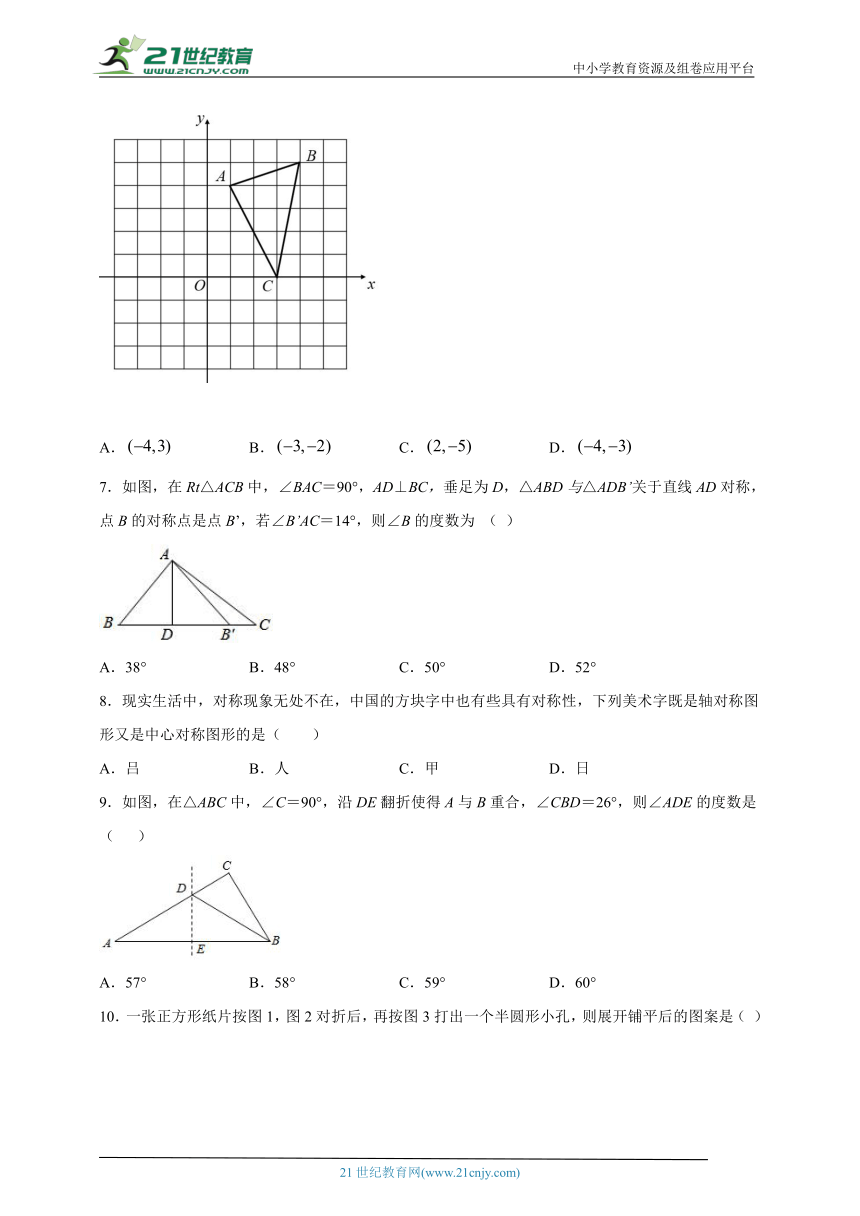
6.是网格中的格点三角形(三角形的各顶点都在网格的交叉点上),如图建立直角坐标系,将该三角形先向下平移2个单位,然后再将平移后的图形沿y轴翻折,得到,则点B对应点的坐标为( )
A. B. C. D.
7.如图,在Rt△ACB中,∠BAC=90°,AD⊥BC,垂足为D,△ABD与△ADB’关于直线AD对称,点B的对称点是点B’,若∠B’AC=14°,则∠B的度数为 ( )
A.38° B.48° C.50° D.52°
8.现实生活中,对称现象无处不在,中国的方块字中也有些具有对称性,下列美术字既是轴对称图形又是中心对称图形的是( )
A.吕 B.人 C.甲 D.日
9.如图,在△ABC中,∠C=90°,沿DE翻折使得A与B重合,∠CBD=26°,则∠ADE的度数是( )
A.57° B.58° C.59° D.60°
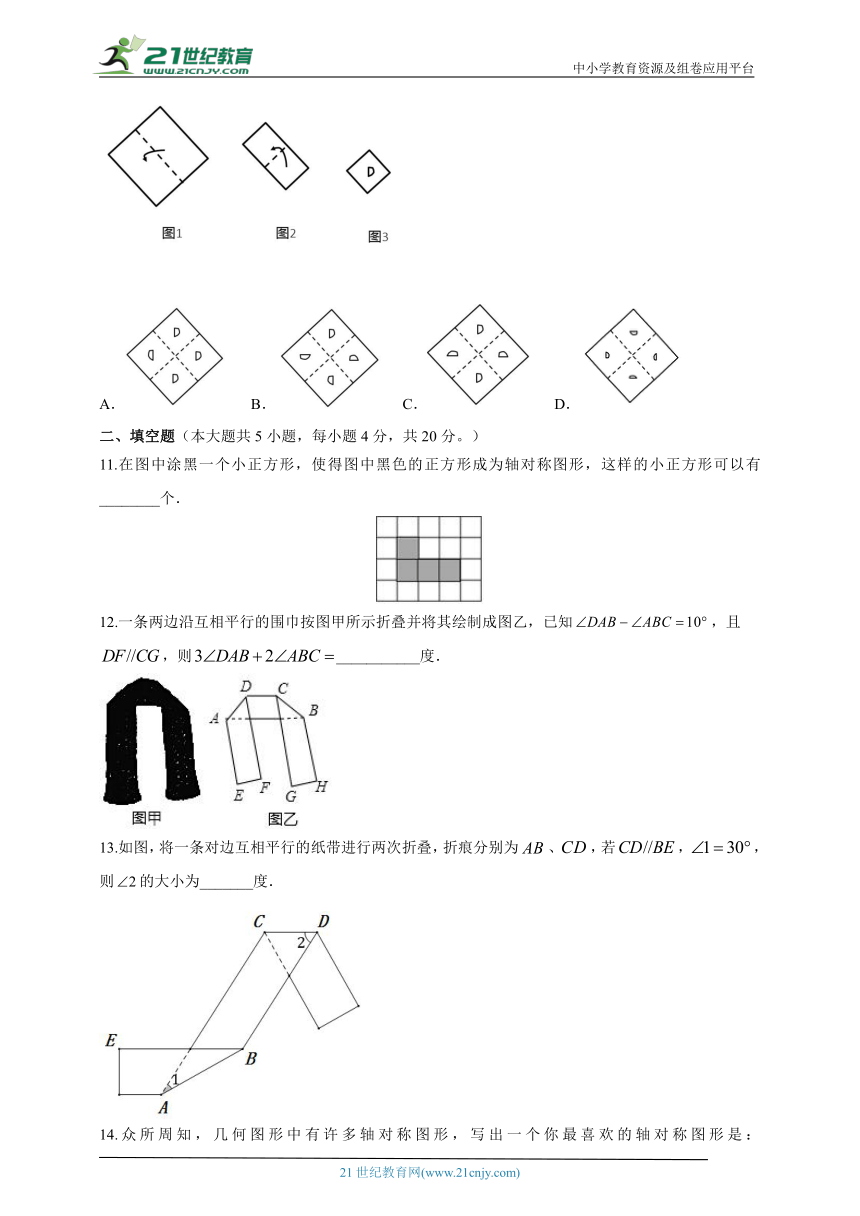
10.一张正方形纸片按图1,图2对折后,再按图3打出一个半圆形小孔,则展开铺平后的图案是( )
A. B. C. D.
二、填空题(本大题共5小题,每小题4分,共20分。)
11.在图中涂黑一个小正方形,使得图中黑色的正方形成为轴对称图形,这样的小正方形可以有________个.
12.一条两边沿互相平行的围巾按图甲所示折叠并将其绘制成图乙,已知,且,则___________度.
13.如图,将一条对边互相平行的纸带进行两次折叠,折痕分别为、,若,,则的大小为_______度.
14.众所周知,几何图形中有许多轴对称图形,写出一个你最喜欢的轴对称图形是:______________________.(答案不唯一)
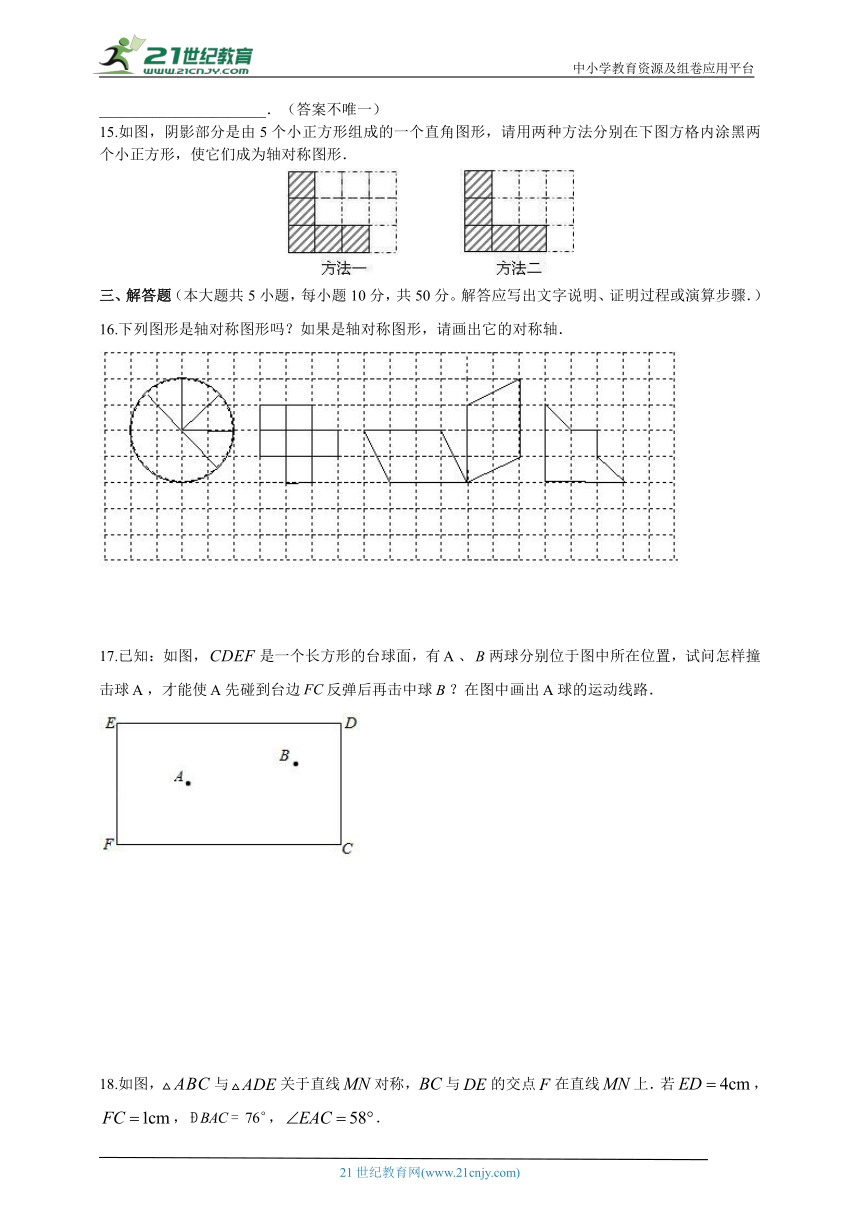
15.如图,阴影部分是由5个小正方形组成的一个直角图形,请用两种方法分别在下图方格内涂黑两个小正方形,使它们成为轴对称图形.
三、解答题(本大题共5小题,每小题10分,共50分。解答应写出文字说明、证明过程或演算步骤.)
16.下列图形是轴对称图形吗?如果是轴对称图形,请画出它的对称轴.
17.已知:如图,是一个长方形的台球面,有、两球分别位于图中所在位置,试问怎样撞击球,才能使先碰到台边反弹后再击中球?在图中画出球的运动线路.
18.如图,与关于直线对称,与的交点在直线上.若,,,.
(1)求出的长度;
(2)求的度数.
19.如图,数轴上、、三个数所对应的点分别为、、,已知,与距离2个单位,与距离6个单位.
(1)①直接写出数、的值;
②求代数式的值;
(2)若将数轴折叠,使得点与点重合,求与点重合的点表示的数.
20.如图,△ABC和△A′B′C′关于直线m对称.
(1)结合图形指出对称点.
(2)连接A、A′,直线m与线段AA′有什么关系?
(3)延长线段AC与A′C′,它们的交点与直线m有怎样的关系?其他对应线段(或其延长线)的交点呢?你发现了什么规律,请叙述出来与同伴交流.
参考答案
选择题
1.【答案】D
【解析】从第一个字母研究,只要能够找到一条对称轴,令这个字母沿这条对称轴折叠后,两边的部分能够互相重合,就是轴对称图形,可以得出:字母H、A、O、M、W、Y、E这七个字母,属于轴对称图形.故选D.
2.【答案】A
【解析】等腰三角形、等边三角形、等腰直角三角形都是轴对称图形,是轴对称图形的有3个.故选A.
3.【答案】C
【解析】由给出的图案,结合轴对称的性质,可知C是旋转一定的角度后与原来的图案对称的,不是一个轴对称图形,故选C.
4.【答案】C
【分析】根据轴对称图形的概念对各选项分析判断即可得到答案.
【详解】A.不是轴对称图形,故本选项错误;
B.不是轴对称图形,故本选项错误;
C.是轴对称图形,故本选项正确;
D.不是轴对称图形,故本选项错误.
故选:C.
5.【答案】C
【分析】由折叠可知,,再根据三角形的外角等于与它不相邻的两个内角的和分别表示出和,进而得出,最终得出答案.
【详解】如图,
如图,设直线与分别交于点,点,
令与的交点为,且,
沿直线翻折,点落在点上,
,
在中,,
在中,,
,
,
即
故选:C.
6.【答案】A
【分析】根据网格求出点B坐标,向下平移2个单位,点 B的横坐标不变,纵坐标减2得对应点B1的坐标,再沿y轴翻折,横坐标变为相反数,纵坐标不变即可得出点B′(-4,3).
【详解】∵点B坐标为(4,5)
向下平移2个单位,得点B对应点的坐标B1(4,5-2),即B1(4,3),
再沿y轴翻折,
点B′(-4,3),
故选择A.
7.【答案】D
【分析】由对称的性质得,根据∠BAC=90°可得,再根据直角三角形两锐角关系求解即可.
【详解】∵△ABD与△ADB’关于直线AD对称,
∴
∵∠BAC=90°,∠B’AC=14°
∴
∴
∴
故选D.
8.【答案】D
【分析】根据轴对称图形与中心对称图形的概念求解.
【详解】A、“吕”字是轴对称图形,不是中心对称图形,故本选项不合题意;
B、“人”字是轴对称图形,不是中心对称图形,故本选项不合题意;
C、“甲”字是轴对称图形,不是中心对称图形,故本选项不合题意;
D、“日”字既是轴对称图形,又是中心对称图形,故本选项符合题意.
故选:D.
9.【答案】B
【分析】求出∠CDB的度数,再根据翻折求出∠ADE的度数即可.
【详解】∵∠C=90°,∠CBD=26°,
∴∠CDB=90°-∠CBD=64°,
∴∠ADB=116°,
由翻折可知,∠ADE=∠BDE=58°;
故选:B.
10.【答案】D
【分析】依据轴对称的性质,将纸片依次展开还原,即可得到正确结论.
【详解】将图3展开可得小孔位于图2中虚线的左右两侧,且关于该虚线对称;
把图2展开可得小孔位于图1中虚线的上下两侧,且关于该虚线对称;
故选:D.
填空题
11.【答案】3
【解析】如图,涂黑一个小正方形,使得图中黑色的正方形成为轴对称图形,这样的小正方形共有3个.
12.【答案】230
【分析】将围巾展开,根据折叠的性质得:则∠ADM=∠ADF,∠KCB=∠BCN,设∠ABC=x,根据平行线的性质得:∠FDC=∠KCG=2x,由平角的定义列式:∠FDC+∠FDM=180°,可得x的值,从而得结论.
【详解】如图乙,将围巾展开,则∠ADM=∠ADF,∠KCB=∠BCN,
设∠ABC=x,则∠DAB=x+10°,
∵CD∥AB,
∴∠ADM=∠DAB=x+10°=∠ADF,
∵DF∥CG,
∴∠FDC=∠KCG=2x,
∵∠FDC+∠FDM=180°,
∴2x+2(x+10°)=180°,
x=40°,
∴3∠DAB+2∠ABC=3(x+10°)+2x=5x+30°=230°,
故答案为:230.
13.【答案】60
【分析】由折叠的性质可得∠3=∠1=30°,从而求得∠4=120°,再根据平行线的性质定理求出∠ACD=∠4=120°,最后再根据平行线性质定理求出∠2=60°.
【详解】如图,延长FA,由折叠的性质,可得∠3=∠1=30°,
∴∠4=180°-30°-30°=120°,
∵CD∥BE,BE∥AF,
∴∠ACD=∠4=120°,
又∵AC∥BD,
∴∠2=180°-∠ACD=180°-120°=60°.
故答案为:60.
14.圆、正三角形、菱形、长方形、正方形、线段等
15.如图所示:
解答题
16.【解析】第一、二、四中图形是轴对称图形,如图所示:
17.【答案】见解析
【分析】首先作出点A关于FC的对称点,再连接交FC于点P,连接AP,PB,可得A球的运动路线.
【详解】如图所示:运动路线:.
18.【答案】(1)=3cm;(2)=18°
【分析】(1)根据△ABC与△ADE关于直线MN对称确定对称点,从而确定对称线段相等即BC=ED,即可求出的值;
(2)根据△ABC与△ADE关于直线MN对称,利用轴对称的性质得出对称角∠EAD=∠BAC,即可解决问题;
【详解】(1)∵△ABC与△ADE关于直线MN对称,ED=4cm,FC=1cm,
∴BC=ED=4cm,
∴BF=BC FC=3cm.
(2)∵△ABC与△ADE关于直线MN对称,∠BAC=76°,∠EAC=58°,
∴∠EAD=∠BAC=76°,
∴∠CAD=∠EAD ∠EAC=76° 58°=18°.
19.【答案】(1)①,;②4;(2)5
【分析】(1)①根据数轴上两点间的距离可求;②将代数式利用完全平方公式化简后,将a、b的值代入后可求;
(2)根据轴对称的性质,设点B与点M重合,利用线段的中点的性质,求出线段DM的长度即可求出点M表示的数.
【详解】(1)①∵
∴,.
②原式=.
(2)设AC的中点为D.
∵AC=AB+BC=2+6=8,
∴.
∴.
设折叠后点B与点M重合,且点M表示的数为m,如图所示.
∴.
∴.
∴.
∴与点重合的点表示的数5.
20.解:(1)对称点有A和A',B和B',C和C'.
(2)连接A、A′,直线m是线段AA′的垂直平分线.
(3)延长线段AC与A′C′,它们的交点在直线m上,其他对应线段(或其延长线)的交点也在直线m上,即若两线段关于直线m对称,且不平行,则它们的交点或它们的延长线的交点在对称轴上.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
人教版八年级上册数学 13.1.1轴对称 同步练习
(考试时间:60分钟 满分:100分)
选择题(本大题共10小题,每小题3分,共30分。下列各题的备选答案中,只有一项是最符合题意的,请选出。)
1.下列字母中:H、F、A、O、M、W、Y、E,轴对称图形的个数是()
A.5 B.4 C.6 D.7
2.等腰三角形、直角三角形、等边三角形、锐角三角形、钝角三角形和等腰直角三角形中,一定是轴对称图形的有()
A.3个 B.4个 C.5个 D.2个
3.下列图案中,不能用折叠剪纸方法得到的是()
A. B. C. D.
4.下列四个图形分别是节能、节水、绿色食品和低碳标志,其中轴对称图形是( )
A. B. C. D.
5.如图,在中,,将沿直线翻折,点落在点的位置,则的度数是( )
A. B. C. D.
6.是网格中的格点三角形(三角形的各顶点都在网格的交叉点上),如图建立直角坐标系,将该三角形先向下平移2个单位,然后再将平移后的图形沿y轴翻折,得到,则点B对应点的坐标为( )
A. B. C. D.
7.如图,在Rt△ACB中,∠BAC=90°,AD⊥BC,垂足为D,△ABD与△ADB’关于直线AD对称,点B的对称点是点B’,若∠B’AC=14°,则∠B的度数为 ( )
A.38° B.48° C.50° D.52°
8.现实生活中,对称现象无处不在,中国的方块字中也有些具有对称性,下列美术字既是轴对称图形又是中心对称图形的是( )
A.吕 B.人 C.甲 D.日
9.如图,在△ABC中,∠C=90°,沿DE翻折使得A与B重合,∠CBD=26°,则∠ADE的度数是( )
A.57° B.58° C.59° D.60°
10.一张正方形纸片按图1,图2对折后,再按图3打出一个半圆形小孔,则展开铺平后的图案是( )
A. B. C. D.
二、填空题(本大题共5小题,每小题4分,共20分。)
11.在图中涂黑一个小正方形,使得图中黑色的正方形成为轴对称图形,这样的小正方形可以有________个.
12.一条两边沿互相平行的围巾按图甲所示折叠并将其绘制成图乙,已知,且,则___________度.
13.如图,将一条对边互相平行的纸带进行两次折叠,折痕分别为、,若,,则的大小为_______度.
14.众所周知,几何图形中有许多轴对称图形,写出一个你最喜欢的轴对称图形是:______________________.(答案不唯一)
15.如图,阴影部分是由5个小正方形组成的一个直角图形,请用两种方法分别在下图方格内涂黑两个小正方形,使它们成为轴对称图形.
三、解答题(本大题共5小题,每小题10分,共50分。解答应写出文字说明、证明过程或演算步骤.)
16.下列图形是轴对称图形吗?如果是轴对称图形,请画出它的对称轴.
17.已知:如图,是一个长方形的台球面,有、两球分别位于图中所在位置,试问怎样撞击球,才能使先碰到台边反弹后再击中球?在图中画出球的运动线路.
18.如图,与关于直线对称,与的交点在直线上.若,,,.
(1)求出的长度;
(2)求的度数.
19.如图,数轴上、、三个数所对应的点分别为、、,已知,与距离2个单位,与距离6个单位.
(1)①直接写出数、的值;
②求代数式的值;
(2)若将数轴折叠,使得点与点重合,求与点重合的点表示的数.
20.如图,△ABC和△A′B′C′关于直线m对称.
(1)结合图形指出对称点.
(2)连接A、A′,直线m与线段AA′有什么关系?
(3)延长线段AC与A′C′,它们的交点与直线m有怎样的关系?其他对应线段(或其延长线)的交点呢?你发现了什么规律,请叙述出来与同伴交流.
参考答案
选择题
1.【答案】D
【解析】从第一个字母研究,只要能够找到一条对称轴,令这个字母沿这条对称轴折叠后,两边的部分能够互相重合,就是轴对称图形,可以得出:字母H、A、O、M、W、Y、E这七个字母,属于轴对称图形.故选D.
2.【答案】A
【解析】等腰三角形、等边三角形、等腰直角三角形都是轴对称图形,是轴对称图形的有3个.故选A.
3.【答案】C
【解析】由给出的图案,结合轴对称的性质,可知C是旋转一定的角度后与原来的图案对称的,不是一个轴对称图形,故选C.
4.【答案】C
【分析】根据轴对称图形的概念对各选项分析判断即可得到答案.
【详解】A.不是轴对称图形,故本选项错误;
B.不是轴对称图形,故本选项错误;
C.是轴对称图形,故本选项正确;
D.不是轴对称图形,故本选项错误.
故选:C.
5.【答案】C
【分析】由折叠可知,,再根据三角形的外角等于与它不相邻的两个内角的和分别表示出和,进而得出,最终得出答案.
【详解】如图,
如图,设直线与分别交于点,点,
令与的交点为,且,
沿直线翻折,点落在点上,
,
在中,,
在中,,
,
,
即
故选:C.
6.【答案】A
【分析】根据网格求出点B坐标,向下平移2个单位,点 B的横坐标不变,纵坐标减2得对应点B1的坐标,再沿y轴翻折,横坐标变为相反数,纵坐标不变即可得出点B′(-4,3).
【详解】∵点B坐标为(4,5)
向下平移2个单位,得点B对应点的坐标B1(4,5-2),即B1(4,3),
再沿y轴翻折,
点B′(-4,3),
故选择A.
7.【答案】D
【分析】由对称的性质得,根据∠BAC=90°可得,再根据直角三角形两锐角关系求解即可.
【详解】∵△ABD与△ADB’关于直线AD对称,
∴
∵∠BAC=90°,∠B’AC=14°
∴
∴
∴
故选D.
8.【答案】D
【分析】根据轴对称图形与中心对称图形的概念求解.
【详解】A、“吕”字是轴对称图形,不是中心对称图形,故本选项不合题意;
B、“人”字是轴对称图形,不是中心对称图形,故本选项不合题意;
C、“甲”字是轴对称图形,不是中心对称图形,故本选项不合题意;
D、“日”字既是轴对称图形,又是中心对称图形,故本选项符合题意.
故选:D.
9.【答案】B
【分析】求出∠CDB的度数,再根据翻折求出∠ADE的度数即可.
【详解】∵∠C=90°,∠CBD=26°,
∴∠CDB=90°-∠CBD=64°,
∴∠ADB=116°,
由翻折可知,∠ADE=∠BDE=58°;
故选:B.
10.【答案】D
【分析】依据轴对称的性质,将纸片依次展开还原,即可得到正确结论.
【详解】将图3展开可得小孔位于图2中虚线的左右两侧,且关于该虚线对称;
把图2展开可得小孔位于图1中虚线的上下两侧,且关于该虚线对称;
故选:D.
填空题
11.【答案】3
【解析】如图,涂黑一个小正方形,使得图中黑色的正方形成为轴对称图形,这样的小正方形共有3个.
12.【答案】230
【分析】将围巾展开,根据折叠的性质得:则∠ADM=∠ADF,∠KCB=∠BCN,设∠ABC=x,根据平行线的性质得:∠FDC=∠KCG=2x,由平角的定义列式:∠FDC+∠FDM=180°,可得x的值,从而得结论.
【详解】如图乙,将围巾展开,则∠ADM=∠ADF,∠KCB=∠BCN,
设∠ABC=x,则∠DAB=x+10°,
∵CD∥AB,
∴∠ADM=∠DAB=x+10°=∠ADF,
∵DF∥CG,
∴∠FDC=∠KCG=2x,
∵∠FDC+∠FDM=180°,
∴2x+2(x+10°)=180°,
x=40°,
∴3∠DAB+2∠ABC=3(x+10°)+2x=5x+30°=230°,
故答案为:230.
13.【答案】60
【分析】由折叠的性质可得∠3=∠1=30°,从而求得∠4=120°,再根据平行线的性质定理求出∠ACD=∠4=120°,最后再根据平行线性质定理求出∠2=60°.
【详解】如图,延长FA,由折叠的性质,可得∠3=∠1=30°,
∴∠4=180°-30°-30°=120°,
∵CD∥BE,BE∥AF,
∴∠ACD=∠4=120°,
又∵AC∥BD,
∴∠2=180°-∠ACD=180°-120°=60°.
故答案为:60.
14.圆、正三角形、菱形、长方形、正方形、线段等
15.如图所示:
解答题
16.【解析】第一、二、四中图形是轴对称图形,如图所示:
17.【答案】见解析
【分析】首先作出点A关于FC的对称点,再连接交FC于点P,连接AP,PB,可得A球的运动路线.
【详解】如图所示:运动路线:.
18.【答案】(1)=3cm;(2)=18°
【分析】(1)根据△ABC与△ADE关于直线MN对称确定对称点,从而确定对称线段相等即BC=ED,即可求出的值;
(2)根据△ABC与△ADE关于直线MN对称,利用轴对称的性质得出对称角∠EAD=∠BAC,即可解决问题;
【详解】(1)∵△ABC与△ADE关于直线MN对称,ED=4cm,FC=1cm,
∴BC=ED=4cm,
∴BF=BC FC=3cm.
(2)∵△ABC与△ADE关于直线MN对称,∠BAC=76°,∠EAC=58°,
∴∠EAD=∠BAC=76°,
∴∠CAD=∠EAD ∠EAC=76° 58°=18°.
19.【答案】(1)①,;②4;(2)5
【分析】(1)①根据数轴上两点间的距离可求;②将代数式利用完全平方公式化简后,将a、b的值代入后可求;
(2)根据轴对称的性质,设点B与点M重合,利用线段的中点的性质,求出线段DM的长度即可求出点M表示的数.
【详解】(1)①∵
∴,.
②原式=.
(2)设AC的中点为D.
∵AC=AB+BC=2+6=8,
∴.
∴.
设折叠后点B与点M重合,且点M表示的数为m,如图所示.
∴.
∴.
∴.
∴与点重合的点表示的数5.
20.解:(1)对称点有A和A',B和B',C和C'.
(2)连接A、A′,直线m是线段AA′的垂直平分线.
(3)延长线段AC与A′C′,它们的交点在直线m上,其他对应线段(或其延长线)的交点也在直线m上,即若两线段关于直线m对称,且不平行,则它们的交点或它们的延长线的交点在对称轴上.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
