1.2 怎样判定三角形相似 第1课时 课件(共20张PPT) 2024-2025学年数学青岛版九年级上册
文档属性
| 名称 | 1.2 怎样判定三角形相似 第1课时 课件(共20张PPT) 2024-2025学年数学青岛版九年级上册 |
|
|
| 格式 | ppt | ||
| 文件大小 | 729.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-17 15:43:08 | ||
图片预览




文档简介
(共20张PPT)
1.2 怎样判定三角形相似
第1课时
l3
a
b
l1
l2
A
B
C
D
E
F
A
B
C
D
E
F
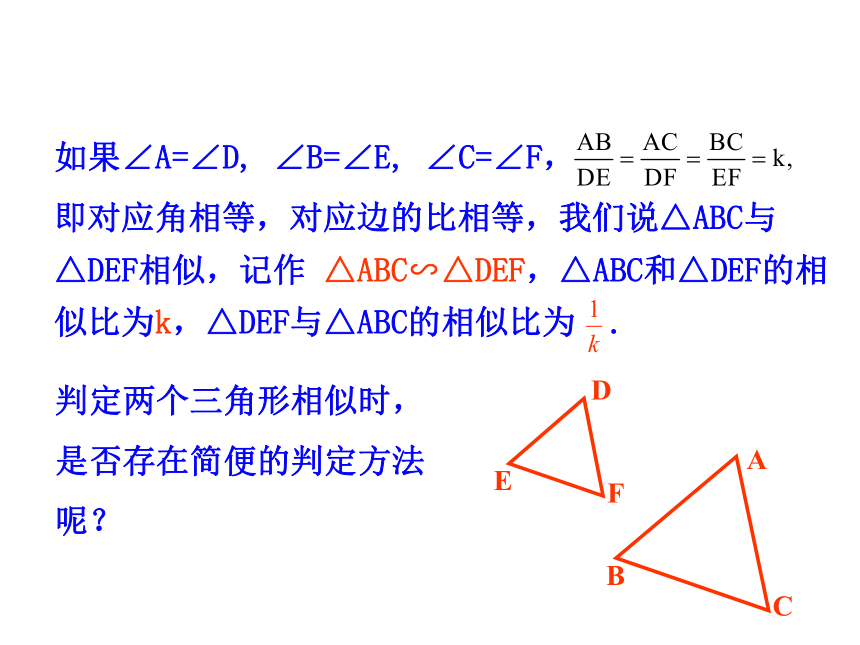
即对应角相等,对应边的比相等,我们说△ABC与
△DEF相似,记作 △ABC∽△DEF,△ABC和△DEF的相
似比为k,△DEF与△ABC的相似比为 .
如果∠A=∠D, ∠B=∠E, ∠C=∠F,
判定两个三角形相似时,是否存在简便的判定方法呢?
1.理解第9个基本事实及其推论.
2.能利用第9个基本事实及其推论解决问题.
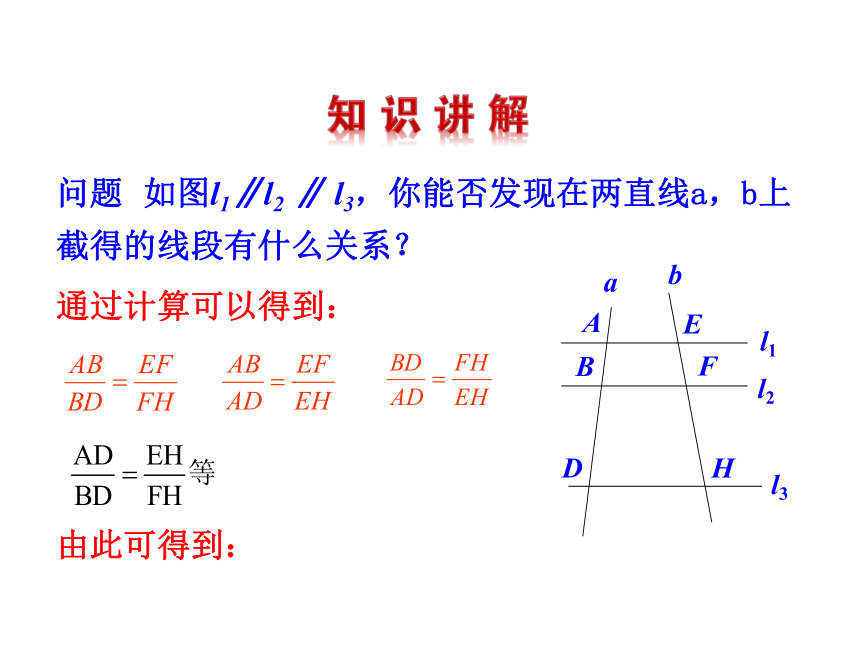
问题 如图l1∥l2 ∥ l3,你能否发现在两直线a,b上截得的线段有什么关系?
l3
l1
l2
A
B
D
E
F
H
a
b
通过计算可以得到:
由此可得到:
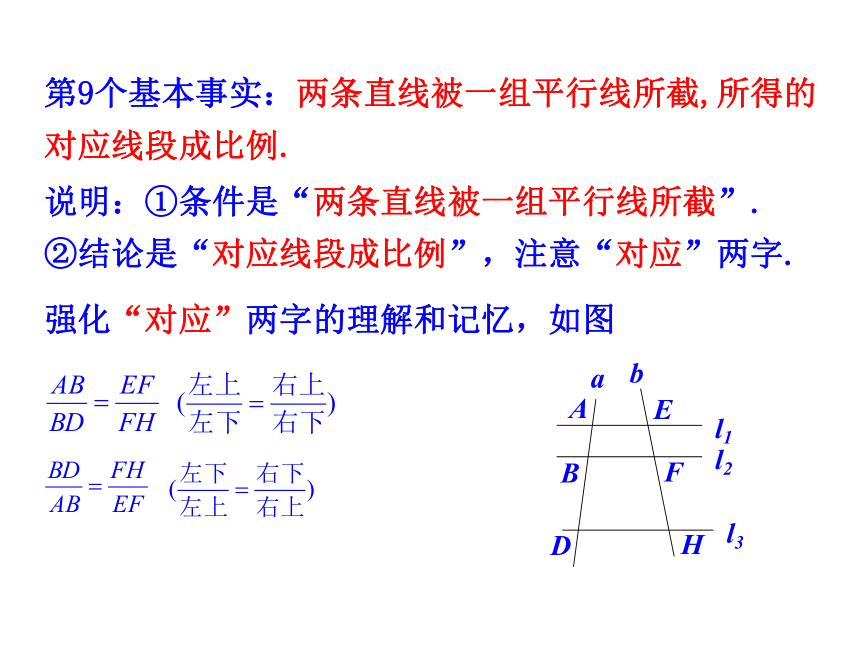
第9个基本事实:两条直线被一组平行线所截,所得的对应线段成比例.
说明:①条件是“两条直线被一组平行线所截”.
②结论是“对应线段成比例”,注意“对应”两字.
强化“对应”两字的理解和记忆,如图
l3
l1
l2
A
B
D
E
F
H
a
b
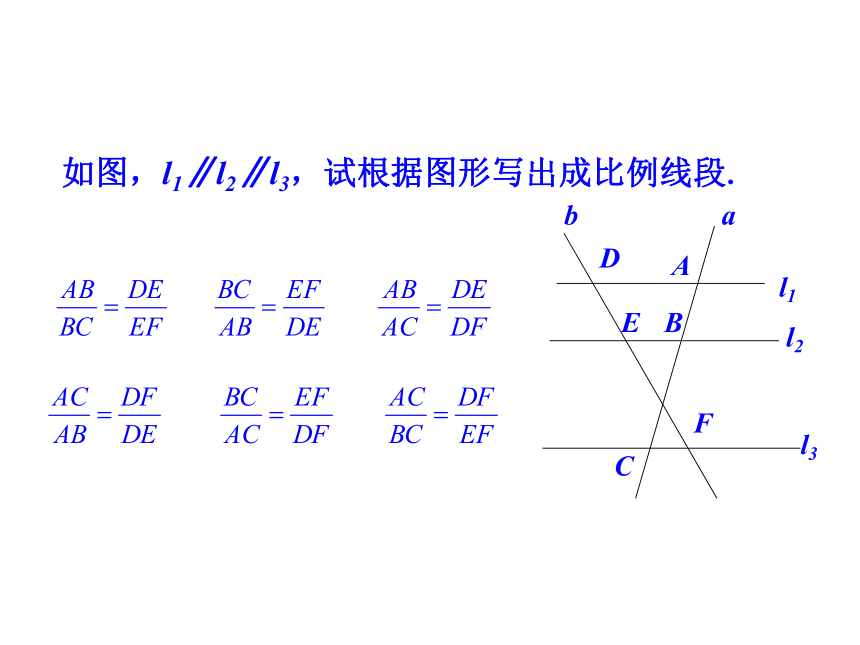
如图,l1∥l2∥l3,试根据图形写出成比例线段.
l3
a
b
l1
l2
A
B
C
D
E
F
已知:在三角形ABC的边AB上任取一点D,作直线DE平行于BC交AC于点E.
A
B
C
D
E
求证:
证明:连接BE、CD,过点E作AB上垂线段h,
l3
l1
l3
l
l
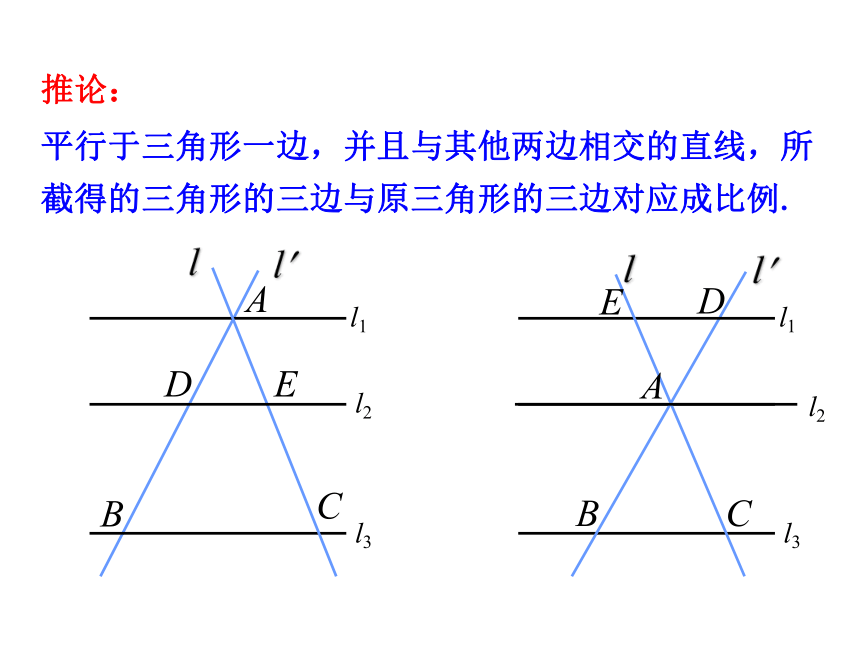
平行于三角形一边,并且与其他两边相交的直线,所截得的三角形的三边与原三角形的三边对应成比例.
A
B
C
D
E
l2
A
B
C
D
E
l1
l
l
推论:
l2
【例题】
如图,已知AA1∥BB1∥CC1,AB=2,BC=3,A1B1=1.5,
求B1C1的长.
解:由平行线分线段成比例定理,得
即
因此
【跟踪训练】
1.如图,在△ABC中,DE∥BC,AC=4,AB=3,EC=1.求AD和BD.
∴AE=3.
解∵AC=4,EC=1,
∵DE∥BC,
∴AD=2.25,
∴BD=0.75.
2.如图,直线AB∥CD∥EF,若AC=3,CE=4,则
的值是________.
3.如图l1∥l2∥l3,试根据图形写出成比例线段.
l3
a
b
l1
l2
A
B
C
D
E
F
一、第9个基本事实与其推论是什么?
三、要熟悉该定理的几种基本图形
二、第9个基本事实:
两条直线被一组平行线所截,所得的对应线段成比例.
(关键要能熟练地找出对应线段)
三、第9个基本事实的推论:
平行于三角形的一边,并且与其他两边相交的直线,所
截得的三角形的三边与原三角形的三边对应成比例.
1.如图,在△ABC中,DG∥EH∥FI∥BC,如果AD=1,
DB=3,那么DG﹕BC=_______.
A
B
C
D
E
F
G
H
I
1﹕4
2. 如图,A、B两点被池塘隔开,在AB外取一点C,连接
AC、BC,在AC上取点M,使AM=3MC,作MN∥AB交BC于点
N,量得MN=38cm,则AB的长为 .
152cm
A
B
C
D
E
F
l1
l3
l2
3
4
2
4.如图,在△ABC中,DE//BC,DF//AC,AE=4,EC=2, BC=8.求BF和CF的长.
F
A
C
B
解: ∵AE=4,EC=2, ∴AC=6.∵DE//BC
∵DF//AC
D
E
A
B
C
D
E
F
E′
F′
5.已知,如图AC、DF被三条平行线所截.
求证:
【解析】过A作DF的平行线分别交BE,CF于点E′,F′,这时
而四边形AE′ED和四边形E′F′FE都是平行四边形,所以AE′=DE,E′F′=EF, ,问题得证.
本来无望的事,大胆尝试,往往能成功。
——莎士比亚
1.2 怎样判定三角形相似
第1课时
l3
a
b
l1
l2
A
B
C
D
E
F
A
B
C
D
E
F
即对应角相等,对应边的比相等,我们说△ABC与
△DEF相似,记作 △ABC∽△DEF,△ABC和△DEF的相
似比为k,△DEF与△ABC的相似比为 .
如果∠A=∠D, ∠B=∠E, ∠C=∠F,
判定两个三角形相似时,是否存在简便的判定方法呢?
1.理解第9个基本事实及其推论.
2.能利用第9个基本事实及其推论解决问题.
问题 如图l1∥l2 ∥ l3,你能否发现在两直线a,b上截得的线段有什么关系?
l3
l1
l2
A
B
D
E
F
H
a
b
通过计算可以得到:
由此可得到:
第9个基本事实:两条直线被一组平行线所截,所得的对应线段成比例.
说明:①条件是“两条直线被一组平行线所截”.
②结论是“对应线段成比例”,注意“对应”两字.
强化“对应”两字的理解和记忆,如图
l3
l1
l2
A
B
D
E
F
H
a
b
如图,l1∥l2∥l3,试根据图形写出成比例线段.
l3
a
b
l1
l2
A
B
C
D
E
F
已知:在三角形ABC的边AB上任取一点D,作直线DE平行于BC交AC于点E.
A
B
C
D
E
求证:
证明:连接BE、CD,过点E作AB上垂线段h,
l3
l1
l3
l
l
平行于三角形一边,并且与其他两边相交的直线,所截得的三角形的三边与原三角形的三边对应成比例.
A
B
C
D
E
l2
A
B
C
D
E
l1
l
l
推论:
l2
【例题】
如图,已知AA1∥BB1∥CC1,AB=2,BC=3,A1B1=1.5,
求B1C1的长.
解:由平行线分线段成比例定理,得
即
因此
【跟踪训练】
1.如图,在△ABC中,DE∥BC,AC=4,AB=3,EC=1.求AD和BD.
∴AE=3.
解∵AC=4,EC=1,
∵DE∥BC,
∴AD=2.25,
∴BD=0.75.
2.如图,直线AB∥CD∥EF,若AC=3,CE=4,则
的值是________.
3.如图l1∥l2∥l3,试根据图形写出成比例线段.
l3
a
b
l1
l2
A
B
C
D
E
F
一、第9个基本事实与其推论是什么?
三、要熟悉该定理的几种基本图形
二、第9个基本事实:
两条直线被一组平行线所截,所得的对应线段成比例.
(关键要能熟练地找出对应线段)
三、第9个基本事实的推论:
平行于三角形的一边,并且与其他两边相交的直线,所
截得的三角形的三边与原三角形的三边对应成比例.
1.如图,在△ABC中,DG∥EH∥FI∥BC,如果AD=1,
DB=3,那么DG﹕BC=_______.
A
B
C
D
E
F
G
H
I
1﹕4
2. 如图,A、B两点被池塘隔开,在AB外取一点C,连接
AC、BC,在AC上取点M,使AM=3MC,作MN∥AB交BC于点
N,量得MN=38cm,则AB的长为 .
152cm
A
B
C
D
E
F
l1
l3
l2
3
4
2
4.如图,在△ABC中,DE//BC,DF//AC,AE=4,EC=2, BC=8.求BF和CF的长.
F
A
C
B
解: ∵AE=4,EC=2, ∴AC=6.∵DE//BC
∵DF//AC
D
E
A
B
C
D
E
F
E′
F′
5.已知,如图AC、DF被三条平行线所截.
求证:
【解析】过A作DF的平行线分别交BE,CF于点E′,F′,这时
而四边形AE′ED和四边形E′F′FE都是平行四边形,所以AE′=DE,E′F′=EF, ,问题得证.
本来无望的事,大胆尝试,往往能成功。
——莎士比亚
同课章节目录
- 第1章 图形的相似
- 1.1 相似多边形
- 1.2 怎样判定三角形相似
- 1.3 相似三角形的性质
- 1.4 图形的位似
- 第2章 解直角三角形
- 2.1 锐角三角比
- 2.2 30°,45°,60°角的三角比
- 2.3 用计算器求锐角三角比
- 2.4 解直角三角形
- 2.5 解直角三角形的应用
- 第3章 对圆的进一步认识
- 3.1 圆的对称性
- 3.2 确定圆的条件
- 3.3 圆周角
- 3.4 直线与圆的位置关系
- 3.5 三角形的内切圆
- 3.6 弧长及扇形面积的计算
- 3.7 正多边形与圆
- 课题学习 图形变换与图案设计
- 第4章 一元二次方程
- 4.1 一元二次方程
- 4.2 用配方法解一元二次方程
- 4.3 用公式法解一元二次方程
- 4.4 用因式分解法解一元二次方程
- 4.5 一元二次方程的应用
- 4.6 一元二次方程根与系数的关系
