1.2 怎样判定三角形相似 第4课时 课件 (共19张PPT)2024-2025学年数学青岛版九年级上册
文档属性
| 名称 | 1.2 怎样判定三角形相似 第4课时 课件 (共19张PPT)2024-2025学年数学青岛版九年级上册 |
|
|
| 格式 | ppt | ||
| 文件大小 | 569.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-17 15:55:23 | ||
图片预览




文档简介
(共19张PPT)
1.2 怎样判定三角形相似
第4课时
A
B
C
D
E
1. 对应角_______, 对应边 的两个三角形,
叫做相似三角形 .
2.相似三角形的____________, 各对应边 .
相等
的比相等
对应角相等
的比相等
3.如何识别两三角形是否相似
∵DE∥BC,
∴△ADE∽△ABC.
平行于三角形一边的直线和其他两边(或两边的延长线)
相交,所构成的三角形与原三角形相似.
D
E
A
B
C
A
B
C
D
E
思考:有没有其他简单的办法判断两个三角形相似
∵DE∥BC,
∴△ADE∽△ACB.
1.理解定理“三边成比例的两个三角形相似.”
2.培养学生与他人交流、合作的意识.
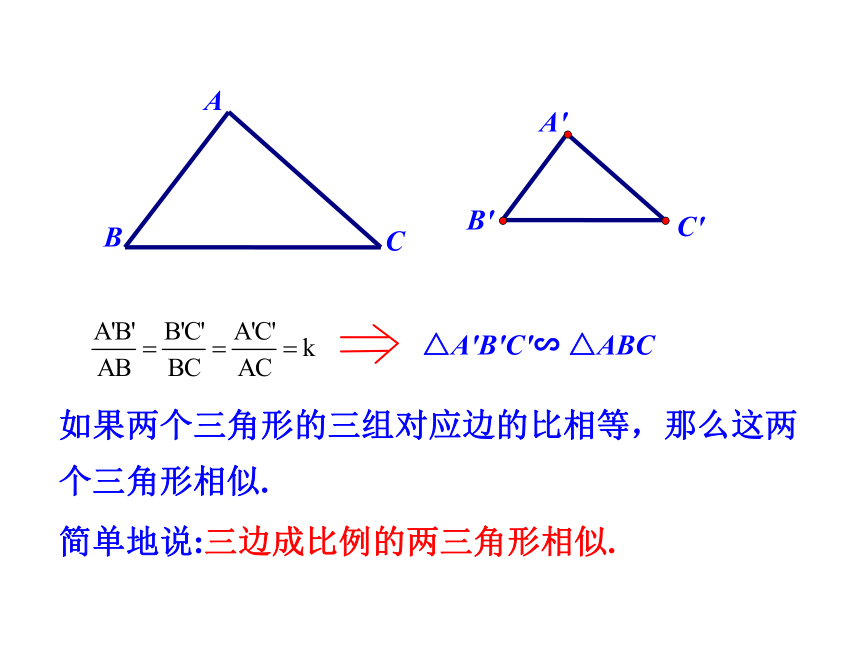
是否有△ABC∽△A′B′C′?
A
B
C
C′
B ′
A′
三边成比例
证明:在△ABC的边AB(或延长线)上截取AD=A′B′,
A′
B′
C′
A
B
C
D
E
过点D作DE∥BC交AC于点E.
又A′B′﹕AB=B′C′﹕BC=C′A′﹕CA.
∴AD﹕AB=AE﹕AC, ∴△ADE∽△ABC.
∵AD=A′B′,∴AD﹕AB=A′B′﹕AB.
∴DE﹕BC=B′C′﹕BC,EA﹕CA=C′A′﹕CA.
因此DE=B′C′,EA=C′A′.
∴△A′B′C′∽△ABC.
∴△ADE≌△A′B′C′,
已知:如图△ABC和△A′B′C′中,A′B′︰AB
=A′C′︰AC=B′C′︰BC.求证:△A′B′C′∽△ABC.
A
B
C
C′
B′
A′
△A′B′C′∽ △ABC
如果两个三角形的三组对应边的比相等,那么这两个三角形相似.
简单地说:三边成比例的两三角形相似.
例1 在△ABC和△A′B′C′中,已知:AB=6cm,
BC=8cm,AC=10cm,A′B′=18cm,B′C′=24cm,
A′C′=30cm.证明△ABC与△A′B′C′相似.
证明:∵
∴
∴△ABC∽△A′B′C′.
【例题】
例2 图中的两个三角形是否相似?为什么?
A
B
C
D
E
F
3cm
4cm
3.5cm
1.8cm
2.4cm
2.1cm
解:在ABC中,BC>AC>AB,
在DEF中,EF>DF>DE,
因此
从而△ ABC ∽△ DEF.
试说明∠BAD=∠CAE.
A
D
C
E
B
∴ΔABC∽ΔADE,
∴∠BAC=∠DAE,
∴∠BAC-∠DAC=∠DAE-∠DAC,
即∠BAD=∠CAE.
【跟踪训练】
答案:相似.
相似比为2﹕1.
设其他两边分别为x,y
①4:2=5:x=6:y
②4:x=5:2=6:y
③4:x=5:y=6:2
④4:y=5:x=6:2
⑤4:2=5:y=6:x
要作两个形状相同的三角形框架,其中一个三角形的三边的长分别为4,5,6,另一个三角形框架的一边长为2,怎样选料可使这两个三角形相似 这个问题有其他答案吗
4
5
6
2
1.平行于三角形一边的直线和其他两边(或两边的延长线)相交,所构成的三角形与原三角形相似.
2.两角分别相等的两个三角形相似.
3.两边成比例且夹角相等的两个三角形相似.
4.三边成比例的两个三角形相似.
相似三角形的判定方法:
1.(泰州·中考)一个铝质三角形框架三条边长分别
为24cm,30cm,36cm,要做一个与它相似的铝质三角
形框架,现有长为27cm,45cm的两根铝材,要求以其
中的一根为一边,从另一根上截下两段(允许有余
料)作为另外两边.截法有( )
A.0种 B. 1种 C. 2种 D. 3种
B
2.(衢州·中考)如图,方格纸中每个小正方形的边长为1,△ABC和△DEF的顶点都在方格纸的格点上.
(1)判断△ABC和△DEF是否相似,并说明理由.
(2)P1,P2,P3,P4,P5,D,F是△DEF边上的7个格点,请在这7个格点中选取3个点作为三角形的顶点,使构成的三角形与△ABC相似(要求写出2个符合条件的三角形,并在图中连接相应线段,不必说明理由).
A
C
B
F
E
D
P1
P2
P3
P4
P5
【解析】(1)△ABC和△DEF相似.根据勾股定理,得 , ,BC=5; , ,
.
∵ ,∴△ABC∽△DEF.
(2)答案不唯一,下面6个三角形中的任意2个均可.
△P2P5D,△P4P5F,△P2P4D,
△P4P5D,△P2P4 P5,△P1FD.
A
C
B
F
E
D
P1
P2
P3
P4
P5
3.(成都·中考)如图,已知线段AB∥CD,AD与BC相交于
点K,E是线段AD上一动点.
(1)若BK= KC,求 的值.
(2)连接BE,若BE平分∠ABC,则当AE= AD时,猜想线段
AB、BC、CD三者之间有怎样的等量关系 请写出你的结论
并予以证明.再探究:当AE= AD (n>2),而其余条件不
变时,线段AB、BC、CD三者之间又有怎样的等量关系
请直接写出你的结论,不必证明.
【解析】(1)∵AB∥CD,BK= KC,∴ = = .
(2)如图所示,分别过C,D作CF∥DG∥BE分别交AB
的延长线于F,G两点,
∵BE∥DG,点E是AD中点,∴AB=BG;∵CD∥FG,CF∥DG,∴四边形CDGF是平行四边形,∴CD=FG.
∵∠ABE=∠EBC,BE∥CF,∴∠EBC=∠BCF,∠ABE=∠BFC,∴∠BFC=∠BCF,∴BC=BF,
∴AB-CD=BG-FG=BF=BC,∴AB=BC+CD.
当AE= AD(n>2)时,(n-1)AB=BC+CD.
真理的大海,让未发现的一切事物躺卧在我的眼前,任我去探寻。
——牛顿
1.2 怎样判定三角形相似
第4课时
A
B
C
D
E
1. 对应角_______, 对应边 的两个三角形,
叫做相似三角形 .
2.相似三角形的____________, 各对应边 .
相等
的比相等
对应角相等
的比相等
3.如何识别两三角形是否相似
∵DE∥BC,
∴△ADE∽△ABC.
平行于三角形一边的直线和其他两边(或两边的延长线)
相交,所构成的三角形与原三角形相似.
D
E
A
B
C
A
B
C
D
E
思考:有没有其他简单的办法判断两个三角形相似
∵DE∥BC,
∴△ADE∽△ACB.
1.理解定理“三边成比例的两个三角形相似.”
2.培养学生与他人交流、合作的意识.
是否有△ABC∽△A′B′C′?
A
B
C
C′
B ′
A′
三边成比例
证明:在△ABC的边AB(或延长线)上截取AD=A′B′,
A′
B′
C′
A
B
C
D
E
过点D作DE∥BC交AC于点E.
又A′B′﹕AB=B′C′﹕BC=C′A′﹕CA.
∴AD﹕AB=AE﹕AC, ∴△ADE∽△ABC.
∵AD=A′B′,∴AD﹕AB=A′B′﹕AB.
∴DE﹕BC=B′C′﹕BC,EA﹕CA=C′A′﹕CA.
因此DE=B′C′,EA=C′A′.
∴△A′B′C′∽△ABC.
∴△ADE≌△A′B′C′,
已知:如图△ABC和△A′B′C′中,A′B′︰AB
=A′C′︰AC=B′C′︰BC.求证:△A′B′C′∽△ABC.
A
B
C
C′
B′
A′
△A′B′C′∽ △ABC
如果两个三角形的三组对应边的比相等,那么这两个三角形相似.
简单地说:三边成比例的两三角形相似.
例1 在△ABC和△A′B′C′中,已知:AB=6cm,
BC=8cm,AC=10cm,A′B′=18cm,B′C′=24cm,
A′C′=30cm.证明△ABC与△A′B′C′相似.
证明:∵
∴
∴△ABC∽△A′B′C′.
【例题】
例2 图中的两个三角形是否相似?为什么?
A
B
C
D
E
F
3cm
4cm
3.5cm
1.8cm
2.4cm
2.1cm
解:在ABC中,BC>AC>AB,
在DEF中,EF>DF>DE,
因此
从而△ ABC ∽△ DEF.
试说明∠BAD=∠CAE.
A
D
C
E
B
∴ΔABC∽ΔADE,
∴∠BAC=∠DAE,
∴∠BAC-∠DAC=∠DAE-∠DAC,
即∠BAD=∠CAE.
【跟踪训练】
答案:相似.
相似比为2﹕1.
设其他两边分别为x,y
①4:2=5:x=6:y
②4:x=5:2=6:y
③4:x=5:y=6:2
④4:y=5:x=6:2
⑤4:2=5:y=6:x
要作两个形状相同的三角形框架,其中一个三角形的三边的长分别为4,5,6,另一个三角形框架的一边长为2,怎样选料可使这两个三角形相似 这个问题有其他答案吗
4
5
6
2
1.平行于三角形一边的直线和其他两边(或两边的延长线)相交,所构成的三角形与原三角形相似.
2.两角分别相等的两个三角形相似.
3.两边成比例且夹角相等的两个三角形相似.
4.三边成比例的两个三角形相似.
相似三角形的判定方法:
1.(泰州·中考)一个铝质三角形框架三条边长分别
为24cm,30cm,36cm,要做一个与它相似的铝质三角
形框架,现有长为27cm,45cm的两根铝材,要求以其
中的一根为一边,从另一根上截下两段(允许有余
料)作为另外两边.截法有( )
A.0种 B. 1种 C. 2种 D. 3种
B
2.(衢州·中考)如图,方格纸中每个小正方形的边长为1,△ABC和△DEF的顶点都在方格纸的格点上.
(1)判断△ABC和△DEF是否相似,并说明理由.
(2)P1,P2,P3,P4,P5,D,F是△DEF边上的7个格点,请在这7个格点中选取3个点作为三角形的顶点,使构成的三角形与△ABC相似(要求写出2个符合条件的三角形,并在图中连接相应线段,不必说明理由).
A
C
B
F
E
D
P1
P2
P3
P4
P5
【解析】(1)△ABC和△DEF相似.根据勾股定理,得 , ,BC=5; , ,
.
∵ ,∴△ABC∽△DEF.
(2)答案不唯一,下面6个三角形中的任意2个均可.
△P2P5D,△P4P5F,△P2P4D,
△P4P5D,△P2P4 P5,△P1FD.
A
C
B
F
E
D
P1
P2
P3
P4
P5
3.(成都·中考)如图,已知线段AB∥CD,AD与BC相交于
点K,E是线段AD上一动点.
(1)若BK= KC,求 的值.
(2)连接BE,若BE平分∠ABC,则当AE= AD时,猜想线段
AB、BC、CD三者之间有怎样的等量关系 请写出你的结论
并予以证明.再探究:当AE= AD (n>2),而其余条件不
变时,线段AB、BC、CD三者之间又有怎样的等量关系
请直接写出你的结论,不必证明.
【解析】(1)∵AB∥CD,BK= KC,∴ = = .
(2)如图所示,分别过C,D作CF∥DG∥BE分别交AB
的延长线于F,G两点,
∵BE∥DG,点E是AD中点,∴AB=BG;∵CD∥FG,CF∥DG,∴四边形CDGF是平行四边形,∴CD=FG.
∵∠ABE=∠EBC,BE∥CF,∴∠EBC=∠BCF,∠ABE=∠BFC,∴∠BFC=∠BCF,∴BC=BF,
∴AB-CD=BG-FG=BF=BC,∴AB=BC+CD.
当AE= AD(n>2)时,(n-1)AB=BC+CD.
真理的大海,让未发现的一切事物躺卧在我的眼前,任我去探寻。
——牛顿
同课章节目录
- 第1章 图形的相似
- 1.1 相似多边形
- 1.2 怎样判定三角形相似
- 1.3 相似三角形的性质
- 1.4 图形的位似
- 第2章 解直角三角形
- 2.1 锐角三角比
- 2.2 30°,45°,60°角的三角比
- 2.3 用计算器求锐角三角比
- 2.4 解直角三角形
- 2.5 解直角三角形的应用
- 第3章 对圆的进一步认识
- 3.1 圆的对称性
- 3.2 确定圆的条件
- 3.3 圆周角
- 3.4 直线与圆的位置关系
- 3.5 三角形的内切圆
- 3.6 弧长及扇形面积的计算
- 3.7 正多边形与圆
- 课题学习 图形变换与图案设计
- 第4章 一元二次方程
- 4.1 一元二次方程
- 4.2 用配方法解一元二次方程
- 4.3 用公式法解一元二次方程
- 4.4 用因式分解法解一元二次方程
- 4.5 一元二次方程的应用
- 4.6 一元二次方程根与系数的关系
