1.3 相似三角形的性质 课件(共18张PPT) 2024-2025学年数学青岛版九年级上册
文档属性
| 名称 | 1.3 相似三角形的性质 课件(共18张PPT) 2024-2025学年数学青岛版九年级上册 |

|
|
| 格式 | ppt | ||
| 文件大小 | 502.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-17 16:00:15 | ||
图片预览




文档简介
(共18张PPT)
1.3 相似三角形的性质
(2)相似三角形有什么性质?根据是什么?相似多边形呢?
根据定义:
对应角相等,
对应边的比相等.
(3)相似三角形的对应边的比叫什么?
相似比
(4)ΔABC与ΔA′B′C′ 的相似 比为k,则ΔA′B′C′
与ΔABC的相似比是多少?
(1)相似三角形有哪些判定方法?
1.理解相似三角形对应线段的比等于相似比,面积的比等于相似比的平方;多边形的周长的比等于相似比,面积的比等于相似比的平方.
2.能应用相似三角形的有关性质解决相关问题.
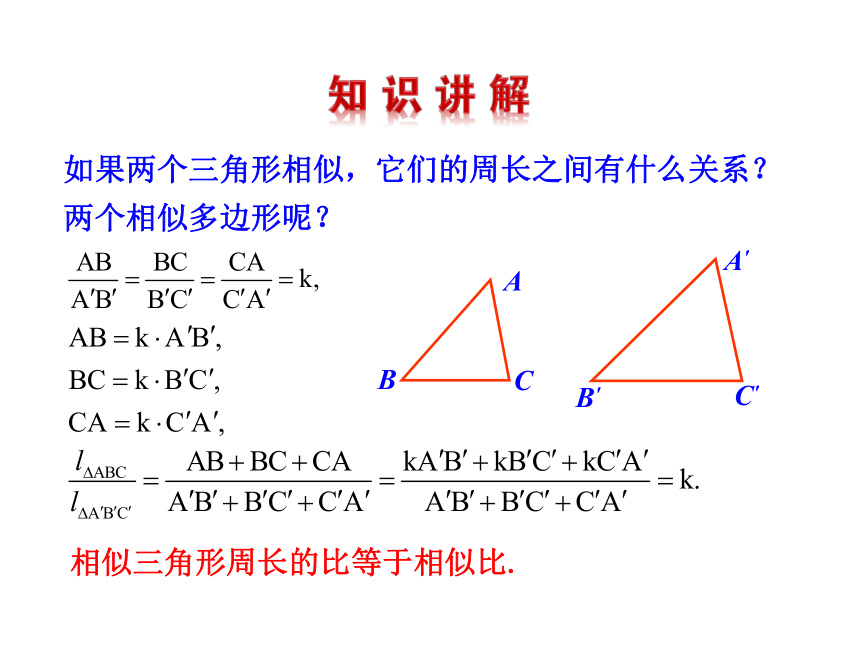
如果两个三角形相似,它们的周长之间有什么关系?
两个相似多边形呢?
A
B
C
A′
B′
C′
相似三角形周长的比等于相似比.
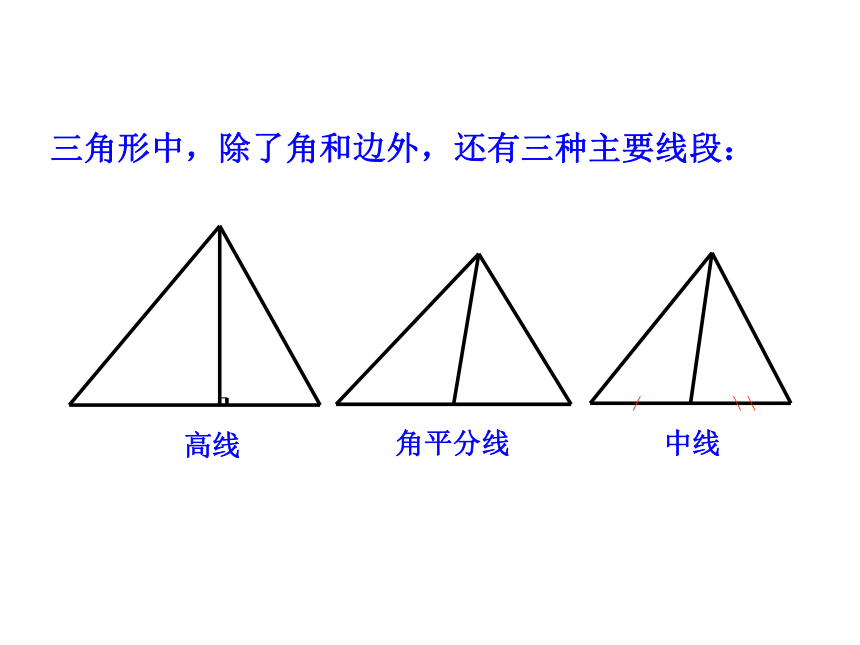
三角形中,除了角和边外,还有三种主要线段:
高线
角平分线
中线
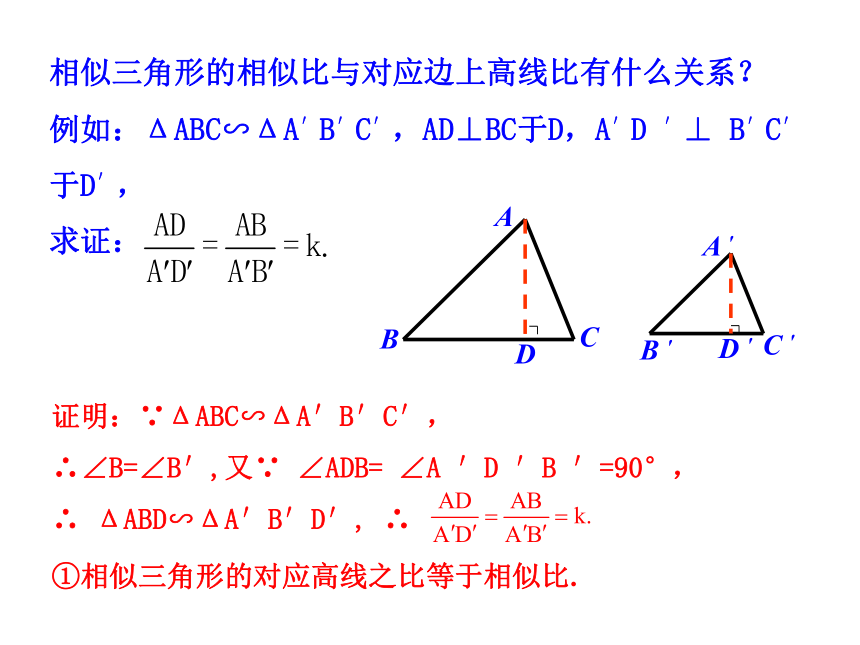
相似三角形的相似比与对应边上高线比有什么关系?
例如:ΔABC∽ΔA′B′C′,AD⊥BC于D,A′D ′⊥ B′C′于D′,
求证:
A
B
C
D
A ′
B ′
C ′
D ′
证明:∵ΔABC∽ΔA′B′C′,
∴∠B=∠B′,又∵ ∠ADB= ∠A ′D ′B ′=90°,
∴ ΔABD∽ΔA′B′D′, ∴
①相似三角形的对应高线之比等于相似比.
角平分线
角平分线
中线
中线
②相似三角形的对应角平分线之比,中线之比,都等于相似比.
(1)如图ΔABC∽ΔA′B′C′,相似比为k,它们的面积比是多少?
相似三角形面积的比等于相似比的平方.
A
B
C
D
A ′
B ′
C ′
D ′
(2)如图,四边形ABCD相似于四边形A′B′C′D′,相似比为k,它们的面积比是多少?
A
B
C
D
A ′
B ′
C ′
D ′
相似多边形面积的比等于相似比的平方.
k2
例 如图在ΔABC 和ΔDEF中,AB=2DE,AC=2DF,
∠A=∠D,ΔABC的周长是24,面积是 ,求ΔDEF
的周长和面积.
A
B
C
D
E
F
【例题】
【解析】
1.(1)已知ΔABC与ΔA′B′C′ 的相似比为2﹕3,则周
长之比为 ,对应边上中线之比为 ,面积
之比为 .
(2)已知ΔABC∽ΔA′B′C′,且面积之比为9﹕4,则周
长之比为 ,相似比为 ,对应边上的高线
之比为 .
2﹕3
4﹕9
3﹕2
3﹕2
3﹕2
2﹕3
【跟踪训练】
2.判断题:
(1)如果把一个三角形各边同时扩大为原来的5倍,
那么它的周长也扩大为原来的5倍. ( )
√
(2)如果把一个三角形的面积扩大为原来的9倍,那
么它的三边也扩大为原来的9倍. ( )
×
(1)相似三角形对应 的比等于相似比.
相似三角形(多边形)的性质:
高线
角平分线
中线
(3)相似三角形面积的比等于相似比的平方.
(2)相似三角形周长的比等于相似比.
1.(潍坊·中考)如图,△ABC中,BC = 2,DE是它的中位
线,下面三个结论:⑴DE=1;⑵△ADE∽△ABC;⑶△ADE的
面积与△ABC的面积之比为1 : 4.其中正确的有( )
A.0 个 B.1个 C.2 个 D.3个
【解析】选D.由中位线定理可知
因为DE∥BC,所以△ADE∽△ABC,相似比为
1﹕2,则面积比为相似比的平方即1﹕4.
2.如图,△ABC中,DE‖BC,且△ADE的面积等于梯形
BCED的面积,则△ADE与△ABC的相似比是_______.
B
A
D
E
C
3.在一张复印出来的纸上,一个多边形的一条边由原图中的2cm变成了6cm,这次复印的放缩比例是多少 这个多边形的面积发生了怎样的变化
答案:这次复印后的图形与原图形的比为3 1,多边形的面积扩大为原来的9倍.
没有不可能,只是暂时没有找到解决问题的办法。
1.3 相似三角形的性质
(2)相似三角形有什么性质?根据是什么?相似多边形呢?
根据定义:
对应角相等,
对应边的比相等.
(3)相似三角形的对应边的比叫什么?
相似比
(4)ΔABC与ΔA′B′C′ 的相似 比为k,则ΔA′B′C′
与ΔABC的相似比是多少?
(1)相似三角形有哪些判定方法?
1.理解相似三角形对应线段的比等于相似比,面积的比等于相似比的平方;多边形的周长的比等于相似比,面积的比等于相似比的平方.
2.能应用相似三角形的有关性质解决相关问题.
如果两个三角形相似,它们的周长之间有什么关系?
两个相似多边形呢?
A
B
C
A′
B′
C′
相似三角形周长的比等于相似比.
三角形中,除了角和边外,还有三种主要线段:
高线
角平分线
中线
相似三角形的相似比与对应边上高线比有什么关系?
例如:ΔABC∽ΔA′B′C′,AD⊥BC于D,A′D ′⊥ B′C′于D′,
求证:
A
B
C
D
A ′
B ′
C ′
D ′
证明:∵ΔABC∽ΔA′B′C′,
∴∠B=∠B′,又∵ ∠ADB= ∠A ′D ′B ′=90°,
∴ ΔABD∽ΔA′B′D′, ∴
①相似三角形的对应高线之比等于相似比.
角平分线
角平分线
中线
中线
②相似三角形的对应角平分线之比,中线之比,都等于相似比.
(1)如图ΔABC∽ΔA′B′C′,相似比为k,它们的面积比是多少?
相似三角形面积的比等于相似比的平方.
A
B
C
D
A ′
B ′
C ′
D ′
(2)如图,四边形ABCD相似于四边形A′B′C′D′,相似比为k,它们的面积比是多少?
A
B
C
D
A ′
B ′
C ′
D ′
相似多边形面积的比等于相似比的平方.
k2
例 如图在ΔABC 和ΔDEF中,AB=2DE,AC=2DF,
∠A=∠D,ΔABC的周长是24,面积是 ,求ΔDEF
的周长和面积.
A
B
C
D
E
F
【例题】
【解析】
1.(1)已知ΔABC与ΔA′B′C′ 的相似比为2﹕3,则周
长之比为 ,对应边上中线之比为 ,面积
之比为 .
(2)已知ΔABC∽ΔA′B′C′,且面积之比为9﹕4,则周
长之比为 ,相似比为 ,对应边上的高线
之比为 .
2﹕3
4﹕9
3﹕2
3﹕2
3﹕2
2﹕3
【跟踪训练】
2.判断题:
(1)如果把一个三角形各边同时扩大为原来的5倍,
那么它的周长也扩大为原来的5倍. ( )
√
(2)如果把一个三角形的面积扩大为原来的9倍,那
么它的三边也扩大为原来的9倍. ( )
×
(1)相似三角形对应 的比等于相似比.
相似三角形(多边形)的性质:
高线
角平分线
中线
(3)相似三角形面积的比等于相似比的平方.
(2)相似三角形周长的比等于相似比.
1.(潍坊·中考)如图,△ABC中,BC = 2,DE是它的中位
线,下面三个结论:⑴DE=1;⑵△ADE∽△ABC;⑶△ADE的
面积与△ABC的面积之比为1 : 4.其中正确的有( )
A.0 个 B.1个 C.2 个 D.3个
【解析】选D.由中位线定理可知
因为DE∥BC,所以△ADE∽△ABC,相似比为
1﹕2,则面积比为相似比的平方即1﹕4.
2.如图,△ABC中,DE‖BC,且△ADE的面积等于梯形
BCED的面积,则△ADE与△ABC的相似比是_______.
B
A
D
E
C
3.在一张复印出来的纸上,一个多边形的一条边由原图中的2cm变成了6cm,这次复印的放缩比例是多少 这个多边形的面积发生了怎样的变化
答案:这次复印后的图形与原图形的比为3 1,多边形的面积扩大为原来的9倍.
没有不可能,只是暂时没有找到解决问题的办法。
同课章节目录
- 第1章 图形的相似
- 1.1 相似多边形
- 1.2 怎样判定三角形相似
- 1.3 相似三角形的性质
- 1.4 图形的位似
- 第2章 解直角三角形
- 2.1 锐角三角比
- 2.2 30°,45°,60°角的三角比
- 2.3 用计算器求锐角三角比
- 2.4 解直角三角形
- 2.5 解直角三角形的应用
- 第3章 对圆的进一步认识
- 3.1 圆的对称性
- 3.2 确定圆的条件
- 3.3 圆周角
- 3.4 直线与圆的位置关系
- 3.5 三角形的内切圆
- 3.6 弧长及扇形面积的计算
- 3.7 正多边形与圆
- 课题学习 图形变换与图案设计
- 第4章 一元二次方程
- 4.1 一元二次方程
- 4.2 用配方法解一元二次方程
- 4.3 用公式法解一元二次方程
- 4.4 用因式分解法解一元二次方程
- 4.5 一元二次方程的应用
- 4.6 一元二次方程根与系数的关系
