1.4 图形的位似 第1课时 课件 (共19张PPT)2024-2025学年数学青岛版九年级上册
文档属性
| 名称 | 1.4 图形的位似 第1课时 课件 (共19张PPT)2024-2025学年数学青岛版九年级上册 |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-17 16:04:56 | ||
图片预览




文档简介
(共19张PPT)
1.4 图形的位似
第1课时
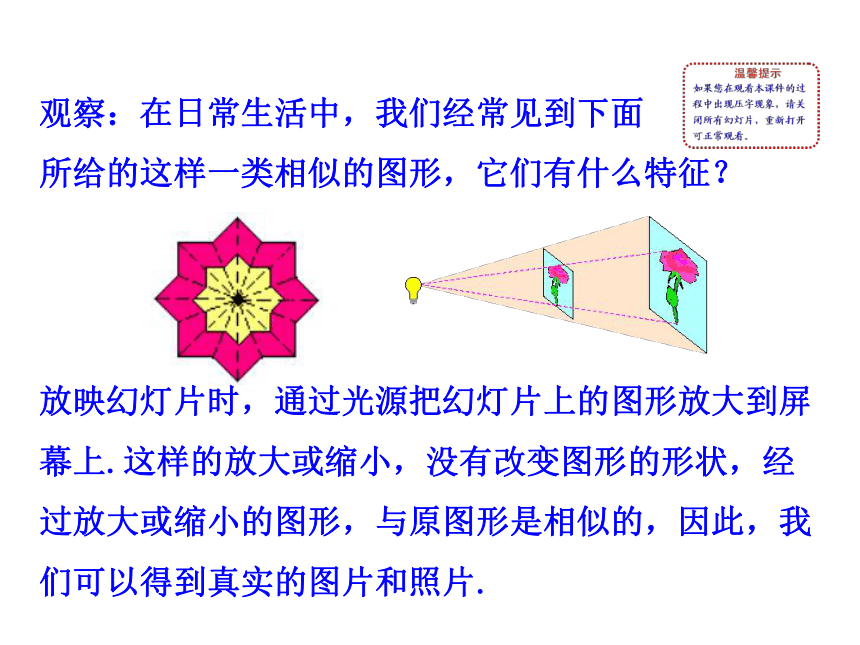
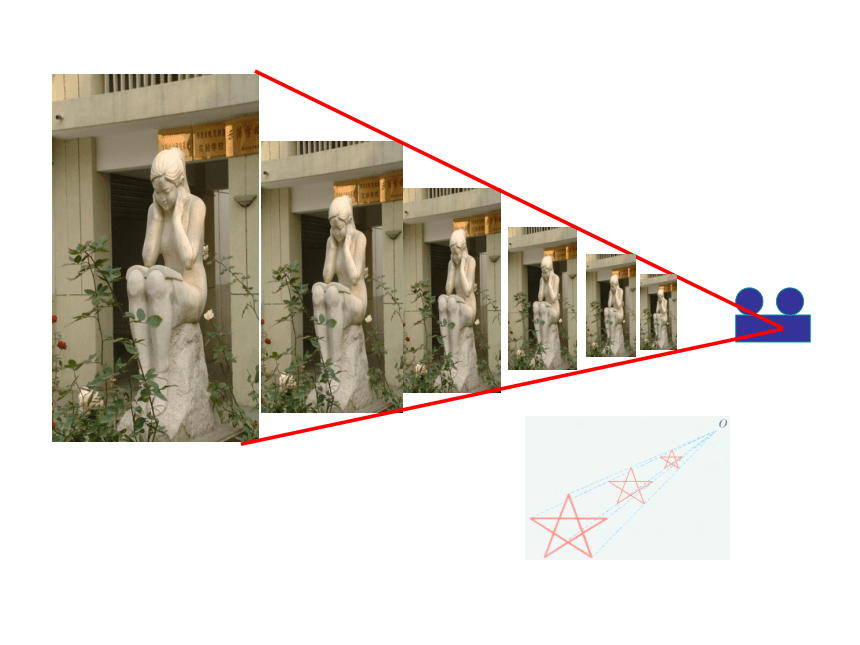
观察:在日常生活中,我们经常见到下面
所给的这样一类相似的图形,它们有什么特征?
放映幻灯片时,通过光源把幻灯片上的图形放大到屏幕上.这样的放大或缩小,没有改变图形的形状,经过放大或缩小的图形,与原图形是相似的,因此,我们可以得到真实的图片和照片.
1.了解位似图形及其有关概念,了解位似与相似的联系和区别,掌握位似图形的性质.
2.掌握位似图形的画法,能够利用作位似图形的方法将一个图形放大或缩小.
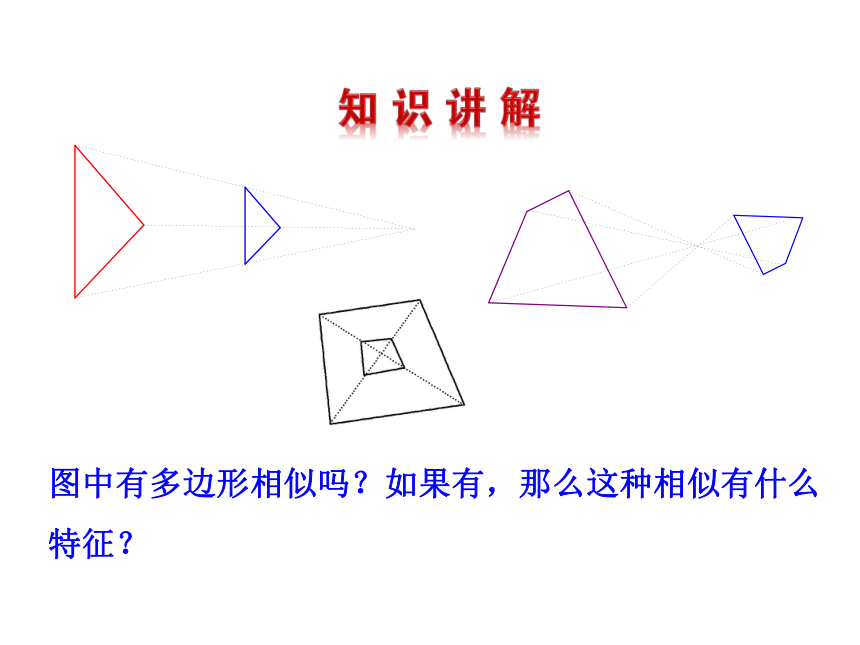
图中有多边形相似吗?如果有,那么这种相似有什么特征?
对应边互相平行(或共线)且每对对应点所在的直线都经过同一点的两个相似多边形叫做位似图形,这个点叫做位似中心.
定义:
例 把图1中的四边形ABCD缩小到原来的 .
分析:把原图形缩小到原来的 ,也就是使新图形上
各顶点到位似中心的距离与原图形各对应顶点到位似
中心的距离之比为1∶2 .
【例题】
作法一:(1)在四边形ABCD外任取一点O;
(2)过点O分别作射线OA,OB,OC,OD;
(3)分别在射线OA,OB,OC,OD上取点
A′,B′,C′,D′,
使得 ;
(4)顺次连接A′B′,B′C′,C′D′,D′A′,得到所要画的四边形A′B′C′D′,如图2.
作法三
当点O在四边形ABCD的一条边上或在四边形ABCD的一个顶点上时,你能作出相应的图形吗?(留作课下训练)
作法二
问:此题目还可以如何画出图形?
′
O
A
B
C
F
●
E
●
D
●
选择以上一种方法将△ABC的三边缩小为原来的 .
【解析】如图,任取一点O,连接AO,BO,CO,并取它
们的中点D,E,F;顺次连接EF,FD,DE,△DEF的三
边就是△ABC相应三边的 .实际上△ABC与△DEF是位
似图形.
【跟踪训练】
如图,D,E分别是AB,AC上的点.
(1)如果DE∥BC,那么 ADE和 ABC是
位似图形吗?为什么?
A
B
C
D
E
(2)如果 ADE和 ABC是位似图形,那么DE∥BC吗?
为什么?
(2)DE∥BC.理由是:
ADE和 ABC是位似图形
ADE∽ ABC
∠ADE=∠B
DE∥BC.
【解析】(1) ADE和 ABC是位似图形.理由是:
DE∥BC
ADE∽ ABC
对应点连线都经过点A
ADE和 ABC是位似图形.
在下图中,(1) (3)中的两个图形是位似图形,(2)中的两个图形不是位似图形.
O
P
(1)
(3)
(2)
通过这节课的学习,你有哪些收获?
1.对应边互相平行(或共线)且每对对应点所在的直线都经过同一点的两个相似多边形叫做位似图形,这个交点叫做位似中心.
2.位似图形的对应点和位似中心在同一条直线上,它们到位似中心的距离之比等于相似比.
1.两个多边形不仅_____,而且 ,
对应边平行(或共线),则这两个图形叫做位似图形,这个
点叫做 .
2.利用位似,可以将一个图形______或_______.
放大
缩小
相似
对应点所在的直线交于一点
位似中心
3.下列图形中,不能看作是位似图形的是___.
③
4.(广州·中考)如图,以点O为
位似中心,将五边形ABCDE放大后
得到五边形A′B′C′D′E′,已
知OA=10cm,OA′=20cm,则五边形
ABCDE的周长与五边形A′B′C′D′E′的周长的比值是____.
解析:由题意得,五边形ABCDE与五边形A′B′C′D′E′
是位似图形,所以五边形ABCDE与五边形A′B′C′D′E′
相似,所以它们的周长的比等于相似比,即等于
答案:
5.(丹东·中考) 如图, 与 是位似图
形,且位似比是1:2,若AB=2cm,则 cm,
并在图中画出位似中心O.
4
′
′
′
o
从来没有人读书,只有人在书中读自己,发现自己或检查自己。
——罗曼·罗兰
1.4 图形的位似
第1课时
观察:在日常生活中,我们经常见到下面
所给的这样一类相似的图形,它们有什么特征?
放映幻灯片时,通过光源把幻灯片上的图形放大到屏幕上.这样的放大或缩小,没有改变图形的形状,经过放大或缩小的图形,与原图形是相似的,因此,我们可以得到真实的图片和照片.
1.了解位似图形及其有关概念,了解位似与相似的联系和区别,掌握位似图形的性质.
2.掌握位似图形的画法,能够利用作位似图形的方法将一个图形放大或缩小.
图中有多边形相似吗?如果有,那么这种相似有什么特征?
对应边互相平行(或共线)且每对对应点所在的直线都经过同一点的两个相似多边形叫做位似图形,这个点叫做位似中心.
定义:
例 把图1中的四边形ABCD缩小到原来的 .
分析:把原图形缩小到原来的 ,也就是使新图形上
各顶点到位似中心的距离与原图形各对应顶点到位似
中心的距离之比为1∶2 .
【例题】
作法一:(1)在四边形ABCD外任取一点O;
(2)过点O分别作射线OA,OB,OC,OD;
(3)分别在射线OA,OB,OC,OD上取点
A′,B′,C′,D′,
使得 ;
(4)顺次连接A′B′,B′C′,C′D′,D′A′,得到所要画的四边形A′B′C′D′,如图2.
作法三
当点O在四边形ABCD的一条边上或在四边形ABCD的一个顶点上时,你能作出相应的图形吗?(留作课下训练)
作法二
问:此题目还可以如何画出图形?
′
O
A
B
C
F
●
E
●
D
●
选择以上一种方法将△ABC的三边缩小为原来的 .
【解析】如图,任取一点O,连接AO,BO,CO,并取它
们的中点D,E,F;顺次连接EF,FD,DE,△DEF的三
边就是△ABC相应三边的 .实际上△ABC与△DEF是位
似图形.
【跟踪训练】
如图,D,E分别是AB,AC上的点.
(1)如果DE∥BC,那么 ADE和 ABC是
位似图形吗?为什么?
A
B
C
D
E
(2)如果 ADE和 ABC是位似图形,那么DE∥BC吗?
为什么?
(2)DE∥BC.理由是:
ADE和 ABC是位似图形
ADE∽ ABC
∠ADE=∠B
DE∥BC.
【解析】(1) ADE和 ABC是位似图形.理由是:
DE∥BC
ADE∽ ABC
对应点连线都经过点A
ADE和 ABC是位似图形.
在下图中,(1) (3)中的两个图形是位似图形,(2)中的两个图形不是位似图形.
O
P
(1)
(3)
(2)
通过这节课的学习,你有哪些收获?
1.对应边互相平行(或共线)且每对对应点所在的直线都经过同一点的两个相似多边形叫做位似图形,这个交点叫做位似中心.
2.位似图形的对应点和位似中心在同一条直线上,它们到位似中心的距离之比等于相似比.
1.两个多边形不仅_____,而且 ,
对应边平行(或共线),则这两个图形叫做位似图形,这个
点叫做 .
2.利用位似,可以将一个图形______或_______.
放大
缩小
相似
对应点所在的直线交于一点
位似中心
3.下列图形中,不能看作是位似图形的是___.
③
4.(广州·中考)如图,以点O为
位似中心,将五边形ABCDE放大后
得到五边形A′B′C′D′E′,已
知OA=10cm,OA′=20cm,则五边形
ABCDE的周长与五边形A′B′C′D′E′的周长的比值是____.
解析:由题意得,五边形ABCDE与五边形A′B′C′D′E′
是位似图形,所以五边形ABCDE与五边形A′B′C′D′E′
相似,所以它们的周长的比等于相似比,即等于
答案:
5.(丹东·中考) 如图, 与 是位似图
形,且位似比是1:2,若AB=2cm,则 cm,
并在图中画出位似中心O.
4
′
′
′
o
从来没有人读书,只有人在书中读自己,发现自己或检查自己。
——罗曼·罗兰
同课章节目录
- 第1章 图形的相似
- 1.1 相似多边形
- 1.2 怎样判定三角形相似
- 1.3 相似三角形的性质
- 1.4 图形的位似
- 第2章 解直角三角形
- 2.1 锐角三角比
- 2.2 30°,45°,60°角的三角比
- 2.3 用计算器求锐角三角比
- 2.4 解直角三角形
- 2.5 解直角三角形的应用
- 第3章 对圆的进一步认识
- 3.1 圆的对称性
- 3.2 确定圆的条件
- 3.3 圆周角
- 3.4 直线与圆的位置关系
- 3.5 三角形的内切圆
- 3.6 弧长及扇形面积的计算
- 3.7 正多边形与圆
- 课题学习 图形变换与图案设计
- 第4章 一元二次方程
- 4.1 一元二次方程
- 4.2 用配方法解一元二次方程
- 4.3 用公式法解一元二次方程
- 4.4 用因式分解法解一元二次方程
- 4.5 一元二次方程的应用
- 4.6 一元二次方程根与系数的关系
