2.2 30°,45°,60°角的三角比 2.3 用计算器求锐角三角比 课件(共25张PPT) 2024-2025学年数学青岛版九年级上册
文档属性
| 名称 | 2.2 30°,45°,60°角的三角比 2.3 用计算器求锐角三角比 课件(共25张PPT) 2024-2025学年数学青岛版九年级上册 |  | |
| 格式 | ppt | ||
| 文件大小 | 788.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-17 16:19:55 | ||
图片预览




文档简介
(共25张PPT)
2.2 30°,45°,60°角的三角比
2.3 用计算器求锐角三角比
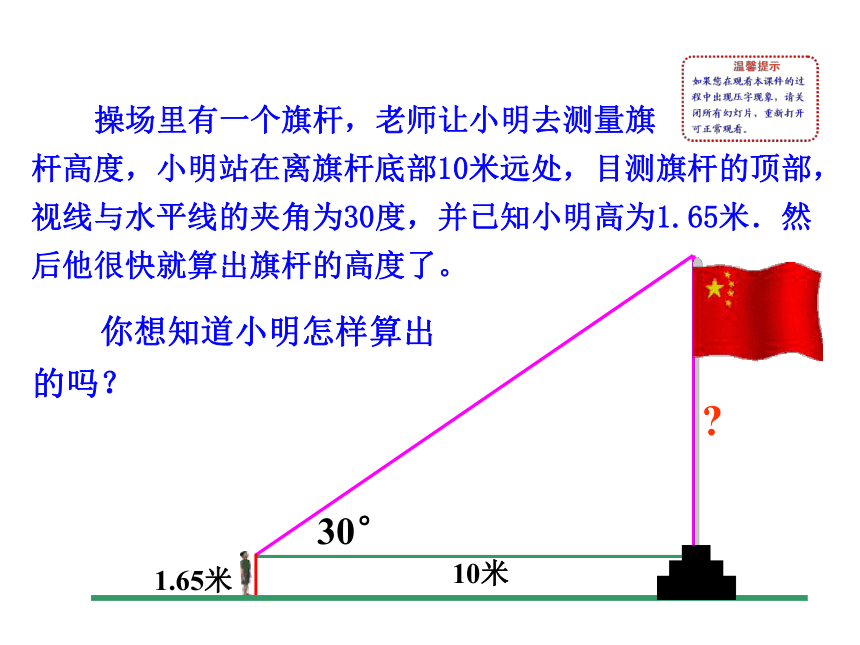
操场里有一个旗杆,老师让小明去测量旗
杆高度,小明站在离旗杆底部10米远处,目测旗杆的顶部,视线与水平线的夹角为30度,并已知小明高为1.65米.然后他很快就算出旗杆的高度了。
1.65米
10米
你想知道小明怎样算出的吗?
30°
1.经历探索30°,45°,60°角的三角比的过程,能够进行有关的推理,进一步体会三角比的意义.
2.能够进行30°,45°,60°角的三角比的计算.
3.能够根据30°,45°,60°的三角比说明相应的锐角的大小.
4.经历用计算器求三角比的探索过程,进一步体会三角比的意义,能够用计算器进行有关三角比的计算.
5.会运用计算器辅助解含三角比计算的实际问题.
如图,观察一副三角板:
它们其中有几个锐角 分别是多少度
(1)sin30°等于多少
┌
┌
30°
60°
45°
45°
(2)cos30°等于多少
(3)tan30°等于多少
请与同伴交流你是怎么想的 又是怎么做的
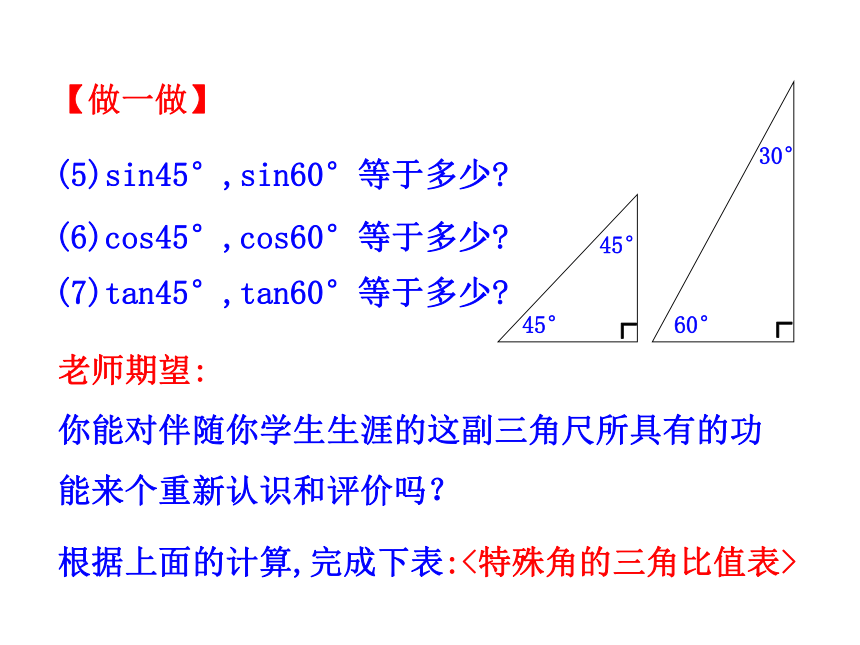
(5)sin45°,sin60°等于多少
(6)cos45°,cos60°等于多少
(7)tan45°,tan60°等于多少
┌
┌
30°
60°
45°
45°
根据上面的计算,完成下表:<特殊角的三角比值表>
老师期望:
你能对伴随你学生生涯的这副三角尺所具有的功能来个重新认识和评价吗?
【做一做】
30° 45° 60°
sinα
cosα
tanα
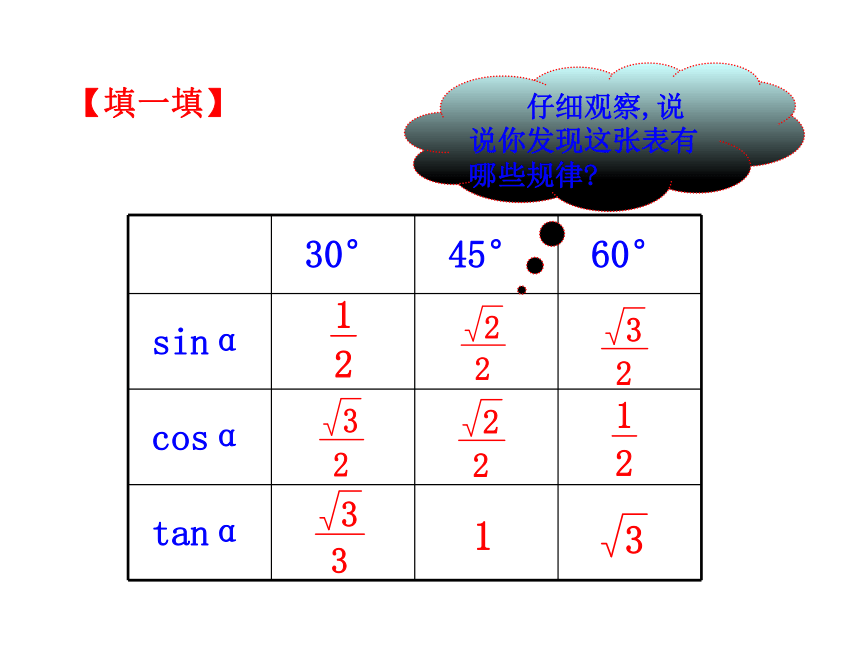
仔细观察,说说你发现这张表有哪些规律
【填一填】
30° 45° 60°
sinα
正弦
cosα
余弦
tanα
正切
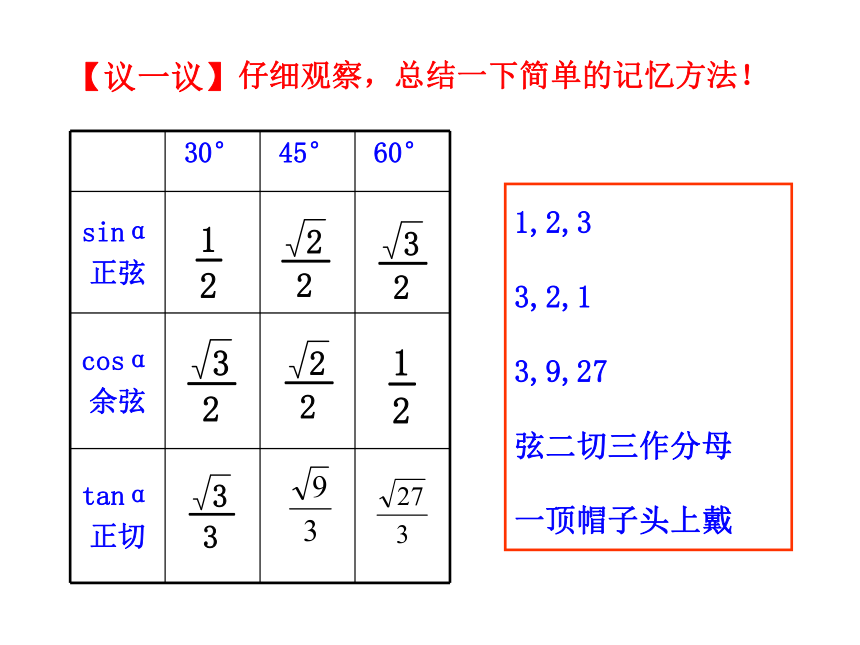
1,2,3
3,2,1
3,9,27
弦二切三作分母
一顶帽子头上戴
仔细观察,总结一下简单的记忆方法!
【议一议】
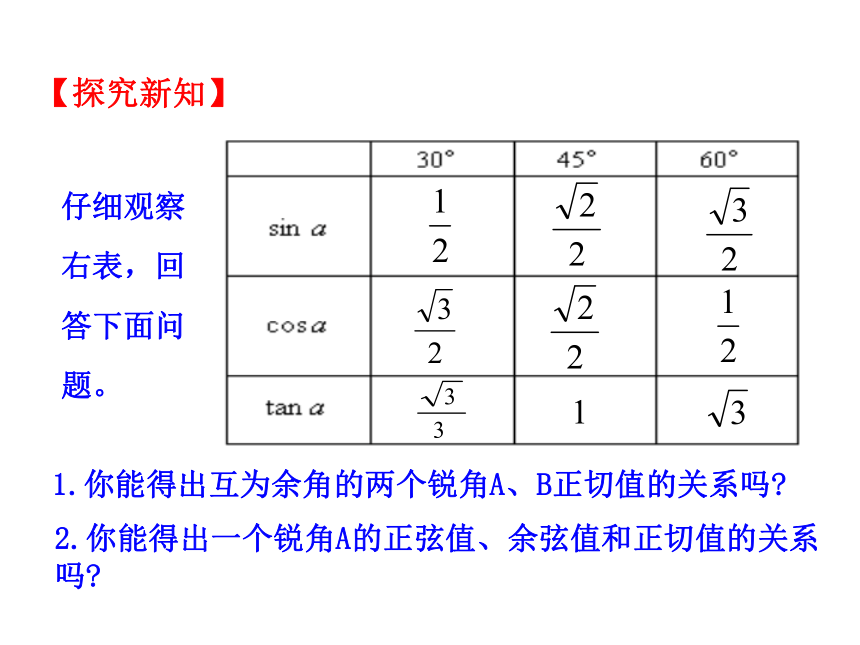
1.你能得出互为余角的两个锐角A、B正切值的关系吗
2.你能得出一个锐角A的正弦值、余弦值和正切值的关系吗
仔细观察
右表,回
答下面问
题。
【探究新知】
sinA=cos(90°-∠A);
一个锐角的正弦值等于这个角余角的余弦值.
cosA=sin(90°-∠A);
一个锐角的余弦值等于这个角余角的正弦值.
tanA·tan(90°-∠A)=1;
一个锐角的正切值与这个角余角的正切值互为倒数.
【归纳升华】
例1.计算:
(1)sin30°+cos45°;
(2)sin260°+cos260°-tan45°.
老师提示:
sin260°表示(sin60°)2,
cos260°表示(cos60°)2,其余类推.
解析: (1)sin30°+cos45°
(2) sin260°+cos260°-tan45°
【例题】
例2.如图:一个小孩荡秋千,秋千链子的长度为2.5m,当秋千向两边摆动时,摆角恰好为60°,且两边摆动的角度相同,求它摆至最高位置时与其摆至最低位置时的高度之差(结果精确到0.01m).
∴最高位置与最低位置的高度差约为0.34m.
∠AOD OD=2.5m,
A
C
O
B
D
┌
解析:如图,根据题意可知,
∴AC=2.5-2.165≈0.34(m).
●
2.5
如果锐角A不是这些特殊角,怎样得到它的三角比呢?
我们可以借助计算器求锐角的三角比.
通过前面的学习我们知道,当锐角A是30°,45°或60°等特殊角时,可以求得这些特殊角的正弦值、余弦值和正切值;
【探究新知】
例3 求sin18°.
第一步:按计算器 键,
sin
第二步:输入角度值18,再输入 和
屏幕显示结果0.309 016 994 4.
【解析】
【例题】
DMS
=
tan
第一步:按计算器 键,
例4 求 tan30°36′.
第二步:输入角度值30,分值36 (可以使用
键),
DMS
屏幕显示答案:0.591 398 351 4.
第一种方法:
第二种方法:
tan
第一步:按计算器 键,
第二步:输入角度值30.6(因为30°36'=30.6°).
屏幕显示答案:0.591 398 351 4.
例5 已知sinA=0.501 8;用计算器求锐角A可以按照下面方法操作:
第一步:按计算器 键,
2nd F
sin
第二步:然后输入正弦值0.501 8.
屏幕显示答案:30.119 158 67(按实际需要进行精确).
利用 键,进一步得到
∠A≈30°7′8.97 "
DMS
求sin63°52′41″的值(精确到0.0001).
解:
按下列顺序依次按键:
显示结果为0.897 859 012.
所以sin63゜52′41″≈0.8979.
【跟踪训练】
1. 30°,45°,60°角的三角比.
2.用计算器求锐角三角比及已知锐角三角比求锐角.
3.一个角的三角比值随着度数的增加是增大还是减小.
通过本课时的学习,需要我们掌握:
1.(黄冈·中考)cos30°=( )
A.
B.
D.
【解析】选C.由三角比的定义知cos30°= .
C.
2.(荆门·中考)计算
sin45°的结果等于( )
答案:选B.
B.1 C.
D.
A.
3.(眉山·中考)如图,已知梯形ABCD中,AD∥BC,
∠B=30°,∠C=60°,AD=4,AB= ,则下底BC的长为
__________.
答案:10
4.(丹东·中考)计算: .
【解析】
.
5.(巴中·中考)已知如图所示,在梯形ABCD中,AD∥BC,AB=AD=DC=8,∠B=60°,连接AC.
(1)求cos∠ACB的值.
(2)若E,F分别是AB,DC的中点,连接EF,求线段EF的长.
cos∠ACB=cos30°= .
∴EF=
=12.
【解析】(1)∵∠B=60°,
∴∠BCD=60°,又
∵AB=AD=DC,
∴∠DAC=∠DCA,
∵AD∥BC,
∴∠DAC=∠BCA,
∴∠DCA=∠BCA,
∴∠ACB=30°,
(2)∵AB=AD=DC=8,∠ACB=30°,∴BC=2AB=16,
∵E,F分别是AB,DC的中点,
【规律方法】
1.记住30°,45°,60°的特殊值及推导方式,可以提高计算速度.
2.会构造直角三角形,充分利用勾股定理的有关知识,结合三角比灵活运用.
第一个青春是上帝给的;第二个青春是靠自己努力的。
2.2 30°,45°,60°角的三角比
2.3 用计算器求锐角三角比
操场里有一个旗杆,老师让小明去测量旗
杆高度,小明站在离旗杆底部10米远处,目测旗杆的顶部,视线与水平线的夹角为30度,并已知小明高为1.65米.然后他很快就算出旗杆的高度了。
1.65米
10米
你想知道小明怎样算出的吗?
30°
1.经历探索30°,45°,60°角的三角比的过程,能够进行有关的推理,进一步体会三角比的意义.
2.能够进行30°,45°,60°角的三角比的计算.
3.能够根据30°,45°,60°的三角比说明相应的锐角的大小.
4.经历用计算器求三角比的探索过程,进一步体会三角比的意义,能够用计算器进行有关三角比的计算.
5.会运用计算器辅助解含三角比计算的实际问题.
如图,观察一副三角板:
它们其中有几个锐角 分别是多少度
(1)sin30°等于多少
┌
┌
30°
60°
45°
45°
(2)cos30°等于多少
(3)tan30°等于多少
请与同伴交流你是怎么想的 又是怎么做的
(5)sin45°,sin60°等于多少
(6)cos45°,cos60°等于多少
(7)tan45°,tan60°等于多少
┌
┌
30°
60°
45°
45°
根据上面的计算,完成下表:<特殊角的三角比值表>
老师期望:
你能对伴随你学生生涯的这副三角尺所具有的功能来个重新认识和评价吗?
【做一做】
30° 45° 60°
sinα
cosα
tanα
仔细观察,说说你发现这张表有哪些规律
【填一填】
30° 45° 60°
sinα
正弦
cosα
余弦
tanα
正切
1,2,3
3,2,1
3,9,27
弦二切三作分母
一顶帽子头上戴
仔细观察,总结一下简单的记忆方法!
【议一议】
1.你能得出互为余角的两个锐角A、B正切值的关系吗
2.你能得出一个锐角A的正弦值、余弦值和正切值的关系吗
仔细观察
右表,回
答下面问
题。
【探究新知】
sinA=cos(90°-∠A);
一个锐角的正弦值等于这个角余角的余弦值.
cosA=sin(90°-∠A);
一个锐角的余弦值等于这个角余角的正弦值.
tanA·tan(90°-∠A)=1;
一个锐角的正切值与这个角余角的正切值互为倒数.
【归纳升华】
例1.计算:
(1)sin30°+cos45°;
(2)sin260°+cos260°-tan45°.
老师提示:
sin260°表示(sin60°)2,
cos260°表示(cos60°)2,其余类推.
解析: (1)sin30°+cos45°
(2) sin260°+cos260°-tan45°
【例题】
例2.如图:一个小孩荡秋千,秋千链子的长度为2.5m,当秋千向两边摆动时,摆角恰好为60°,且两边摆动的角度相同,求它摆至最高位置时与其摆至最低位置时的高度之差(结果精确到0.01m).
∴最高位置与最低位置的高度差约为0.34m.
∠AOD OD=2.5m,
A
C
O
B
D
┌
解析:如图,根据题意可知,
∴AC=2.5-2.165≈0.34(m).
●
2.5
如果锐角A不是这些特殊角,怎样得到它的三角比呢?
我们可以借助计算器求锐角的三角比.
通过前面的学习我们知道,当锐角A是30°,45°或60°等特殊角时,可以求得这些特殊角的正弦值、余弦值和正切值;
【探究新知】
例3 求sin18°.
第一步:按计算器 键,
sin
第二步:输入角度值18,再输入 和
屏幕显示结果0.309 016 994 4.
【解析】
【例题】
DMS
=
tan
第一步:按计算器 键,
例4 求 tan30°36′.
第二步:输入角度值30,分值36 (可以使用
键),
DMS
屏幕显示答案:0.591 398 351 4.
第一种方法:
第二种方法:
tan
第一步:按计算器 键,
第二步:输入角度值30.6(因为30°36'=30.6°).
屏幕显示答案:0.591 398 351 4.
例5 已知sinA=0.501 8;用计算器求锐角A可以按照下面方法操作:
第一步:按计算器 键,
2nd F
sin
第二步:然后输入正弦值0.501 8.
屏幕显示答案:30.119 158 67(按实际需要进行精确).
利用 键,进一步得到
∠A≈30°7′8.97 "
DMS
求sin63°52′41″的值(精确到0.0001).
解:
按下列顺序依次按键:
显示结果为0.897 859 012.
所以sin63゜52′41″≈0.8979.
【跟踪训练】
1. 30°,45°,60°角的三角比.
2.用计算器求锐角三角比及已知锐角三角比求锐角.
3.一个角的三角比值随着度数的增加是增大还是减小.
通过本课时的学习,需要我们掌握:
1.(黄冈·中考)cos30°=( )
A.
B.
D.
【解析】选C.由三角比的定义知cos30°= .
C.
2.(荆门·中考)计算
sin45°的结果等于( )
答案:选B.
B.1 C.
D.
A.
3.(眉山·中考)如图,已知梯形ABCD中,AD∥BC,
∠B=30°,∠C=60°,AD=4,AB= ,则下底BC的长为
__________.
答案:10
4.(丹东·中考)计算: .
【解析】
.
5.(巴中·中考)已知如图所示,在梯形ABCD中,AD∥BC,AB=AD=DC=8,∠B=60°,连接AC.
(1)求cos∠ACB的值.
(2)若E,F分别是AB,DC的中点,连接EF,求线段EF的长.
cos∠ACB=cos30°= .
∴EF=
=12.
【解析】(1)∵∠B=60°,
∴∠BCD=60°,又
∵AB=AD=DC,
∴∠DAC=∠DCA,
∵AD∥BC,
∴∠DAC=∠BCA,
∴∠DCA=∠BCA,
∴∠ACB=30°,
(2)∵AB=AD=DC=8,∠ACB=30°,∴BC=2AB=16,
∵E,F分别是AB,DC的中点,
【规律方法】
1.记住30°,45°,60°的特殊值及推导方式,可以提高计算速度.
2.会构造直角三角形,充分利用勾股定理的有关知识,结合三角比灵活运用.
第一个青春是上帝给的;第二个青春是靠自己努力的。
同课章节目录
- 第1章 图形的相似
- 1.1 相似多边形
- 1.2 怎样判定三角形相似
- 1.3 相似三角形的性质
- 1.4 图形的位似
- 第2章 解直角三角形
- 2.1 锐角三角比
- 2.2 30°,45°,60°角的三角比
- 2.3 用计算器求锐角三角比
- 2.4 解直角三角形
- 2.5 解直角三角形的应用
- 第3章 对圆的进一步认识
- 3.1 圆的对称性
- 3.2 确定圆的条件
- 3.3 圆周角
- 3.4 直线与圆的位置关系
- 3.5 三角形的内切圆
- 3.6 弧长及扇形面积的计算
- 3.7 正多边形与圆
- 课题学习 图形变换与图案设计
- 第4章 一元二次方程
- 4.1 一元二次方程
- 4.2 用配方法解一元二次方程
- 4.3 用公式法解一元二次方程
- 4.4 用因式分解法解一元二次方程
- 4.5 一元二次方程的应用
- 4.6 一元二次方程根与系数的关系
