2.4 解直角三角形 课件(共22张PPT) 2024-2025学年数学青岛版九年级上册
文档属性
| 名称 | 2.4 解直角三角形 课件(共22张PPT) 2024-2025学年数学青岛版九年级上册 |

|
|
| 格式 | ppt | ||
| 文件大小 | 675.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-17 16:21:26 | ||
图片预览







文档简介
(共22张PPT)
2.4 解直角三角形
A
C
B
c
b
a
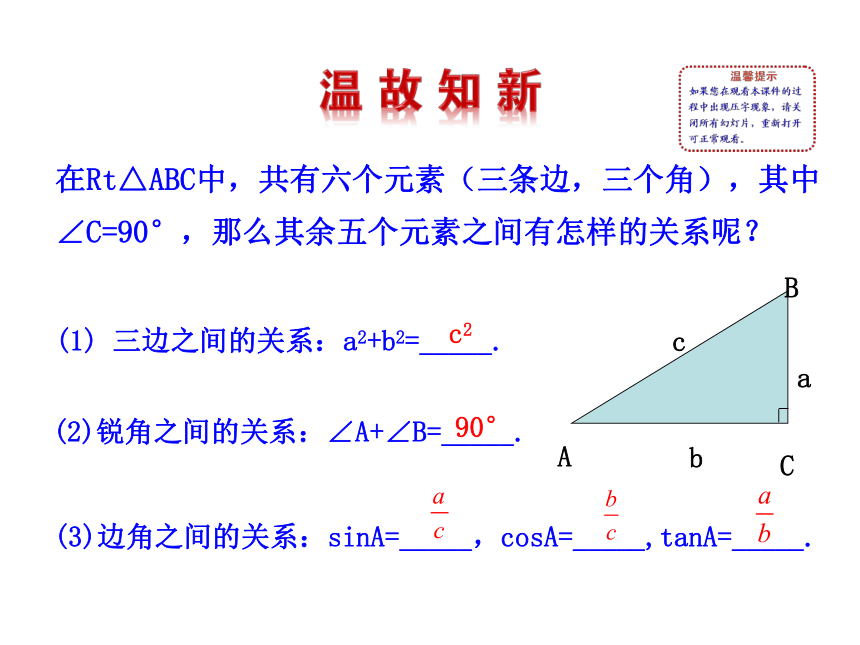
(1) 三边之间的关系:a2+b2=_____.
(2)锐角之间的关系:∠A+∠B=_____.
(3)边角之间的关系:sinA=_____,cosA=_____,tanA=_____.
在Rt△ABC中,共有六个元素(三条边,三个角),其中∠C=90°,那么其余五个元素之间有怎样的关系呢?
c2
90°
1.明确直角三角形中五个元素的关系和解直角三角形的概念.
2.会运用勾股定理,直角三角形的两个锐角互余及锐角三角比解直角三角形.
3.通过解直角三角形的学习,培养分析问题,解决问题的能力,渗透数形结合的思想.
做一做:根据下列每一组条件,能画出多少个直角三角形(全等的直角三角形算一个)?
(1)一个锐角为40 .
(2)一个锐角为40 ,它的邻边长为3cm.
(3)一个锐角为40 ,它的对边长为3cm.
(4)一个锐角为40 ,它的斜边长为3cm.
(5)斜边长为4cm,一条直角边长为3cm.
(无数个)
(一个)
(一个)
(一个)
(一个)
从这些问题的结论,你猜想有什么规律?
根据以上条件可以求出塔身中心线与垂直中心线的夹角.你愿意试着计算一下吗?
如图,设塔顶中心点为B,塔身中心线与垂直中心线的夹
角为A,过B点向垂直中心线引垂线,垂足为点C(如
图),在Rt△ABC中,∠C=90°,BC=5.2m,AB=54.5m.
A
B
C
利用计算器计算可得
将上述问题推广到一般情形,就是:已知直角三角形的斜边和一条直角边,求它的锐角的度数.
在Rt△ABC中,
(1)根据∠A= 60°,斜边AB=30,
A
你发现了什么
B
C
∠B AC BC
∠A ∠B AB
一角一边
(2)根据AC= ,BC=
你能求出这个三角形的其他元素吗?
(3)根据∠A=60°,∠B=30°,
你能求出这个三角形的其他元素吗
不能
你能求出这个三角形的其他元素吗
两角
两边
【合作探究】
在直角三角形的六个元素中,除直角外,如果知道两个元素, (其中至少有一个是边),
就可以求出其余三个元素.
由直角三角形中已知的元素求出未知元素的过程,叫做解直角三角形.
【归纳升华】
(2)两锐角之间的关系
∠A+∠B=90°
(3)边角之间的关系
(1)三边之间的关系
A
B
a
b
c
C
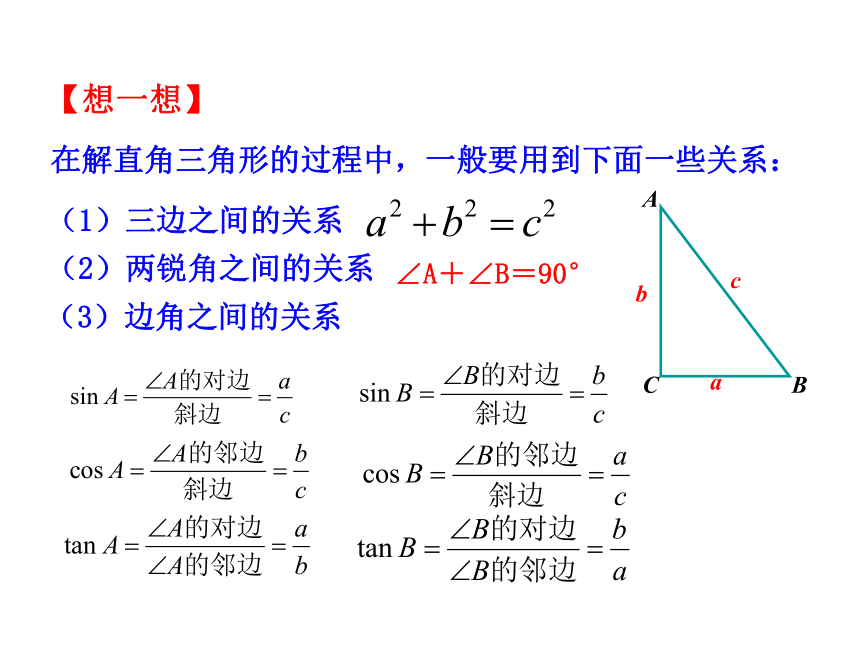
在解直角三角形的过程中,一般要用到下面一些关系:
【想一想】
解直角三角形
1.两锐角之间的关系:
2.三边之间的关系:
3.边角之间的关系
∠A+∠B=90°.
a2+b2=c2.
A
C
B
c
b
a
例1 如图,在Rt△ABC中,∠C=90°,
解这个直角三角形.
A
B
C
【例题】
例2 如图,在Rt△ABC中,∠B=35°,b=20,解这个直角三角形(精确到0.1).
A
B
C
a
b
c
20
35°
你还有其他方法求出c吗?
在下列直角三角形中不能求解的是( )
A.已知一直角边一锐角
B.已知一斜边一锐角
C.已知两边
D.已知两角
D
【跟踪训练】
1.解直角三角形的关键是找到与已知和未知相关联的直角三角形,当图形中没有直角三角形时,要通过作辅助线构造直角三角形(作某边上的高是常用的辅助线).
2.一些解直角三角形的问题往往与其他知识联系,所以要形成知识结构,要把解直角三角形作为一种工具,能在解决各种数学问题时合理运用.
1.(广东·中考)如图,已知Rt△ABC中,斜边BC上的高
AD=4,cosB= ,则AC=____________。
【解析】因为∠BAC=90°,AD是斜边BC上的高,所以
∠B=∠CAD;因为cosB= ,所以在Rt△ADC中,
cos∠CAD= =cosB= ,又因为AD=4,所以AC=5.
答案:5
A
B
C
D
2.(重庆·中考)已知:如图,在Rt△ABC中∠C=90°, .点D为BC边上一点且BD=2AD, ∠ADC=60°,求△ABC的周长.(结果保留根号)
在Rt△ADC中
∵
,∴
∴
在Rt △ABC中
∴
的周长
∵
∴
【解析】
.
.
.
,
,
,
.
3.已知Rt△ABC中,∠C=90°,根据下列条件解直角三角形.
(1)b=5,∠A=30°;(2)
解:(1)∠B=90 –30 =60 .
(2)
∴∠A=30 ,∠B=60 .
由 ,得
4.在Rt△ABC中,∠C=90°,AB=15,
求△ABC的周长和tanA的值.
解:在Rt△ABC中,∠C=90°,AB=15,
∴△ABC的周长为36,
5.(嘉兴·中考)设计建造一条道路,路基的横断面为梯
形ABCD,如图(单位:m).设路基高为h,两侧与水平面
的夹角分别为α和β.已知 h=2,α=45°,CD=10,
(1)求路基底部AB的宽.
(2)修筑这样的路基1 000m,需要多少土石方?
在Rt△ADE中,∵
在Rt△CFB中,∵
∴
在梯形ABCD中,又∵EF=CD=10,
∴AB=AE+EF+FB=16(m).
(2)在梯形ABCD中,∵AB=16,
∴修筑1 000m路基,需要土石方:
于F ,
于E,则
【解析】(1)作
∴面积为
(m ),
人生伟业的建立 ,不在能知,而在能行。
2.4 解直角三角形
A
C
B
c
b
a
(1) 三边之间的关系:a2+b2=_____.
(2)锐角之间的关系:∠A+∠B=_____.
(3)边角之间的关系:sinA=_____,cosA=_____,tanA=_____.
在Rt△ABC中,共有六个元素(三条边,三个角),其中∠C=90°,那么其余五个元素之间有怎样的关系呢?
c2
90°
1.明确直角三角形中五个元素的关系和解直角三角形的概念.
2.会运用勾股定理,直角三角形的两个锐角互余及锐角三角比解直角三角形.
3.通过解直角三角形的学习,培养分析问题,解决问题的能力,渗透数形结合的思想.
做一做:根据下列每一组条件,能画出多少个直角三角形(全等的直角三角形算一个)?
(1)一个锐角为40 .
(2)一个锐角为40 ,它的邻边长为3cm.
(3)一个锐角为40 ,它的对边长为3cm.
(4)一个锐角为40 ,它的斜边长为3cm.
(5)斜边长为4cm,一条直角边长为3cm.
(无数个)
(一个)
(一个)
(一个)
(一个)
从这些问题的结论,你猜想有什么规律?
根据以上条件可以求出塔身中心线与垂直中心线的夹角.你愿意试着计算一下吗?
如图,设塔顶中心点为B,塔身中心线与垂直中心线的夹
角为A,过B点向垂直中心线引垂线,垂足为点C(如
图),在Rt△ABC中,∠C=90°,BC=5.2m,AB=54.5m.
A
B
C
利用计算器计算可得
将上述问题推广到一般情形,就是:已知直角三角形的斜边和一条直角边,求它的锐角的度数.
在Rt△ABC中,
(1)根据∠A= 60°,斜边AB=30,
A
你发现了什么
B
C
∠B AC BC
∠A ∠B AB
一角一边
(2)根据AC= ,BC=
你能求出这个三角形的其他元素吗?
(3)根据∠A=60°,∠B=30°,
你能求出这个三角形的其他元素吗
不能
你能求出这个三角形的其他元素吗
两角
两边
【合作探究】
在直角三角形的六个元素中,除直角外,如果知道两个元素, (其中至少有一个是边),
就可以求出其余三个元素.
由直角三角形中已知的元素求出未知元素的过程,叫做解直角三角形.
【归纳升华】
(2)两锐角之间的关系
∠A+∠B=90°
(3)边角之间的关系
(1)三边之间的关系
A
B
a
b
c
C
在解直角三角形的过程中,一般要用到下面一些关系:
【想一想】
解直角三角形
1.两锐角之间的关系:
2.三边之间的关系:
3.边角之间的关系
∠A+∠B=90°.
a2+b2=c2.
A
C
B
c
b
a
例1 如图,在Rt△ABC中,∠C=90°,
解这个直角三角形.
A
B
C
【例题】
例2 如图,在Rt△ABC中,∠B=35°,b=20,解这个直角三角形(精确到0.1).
A
B
C
a
b
c
20
35°
你还有其他方法求出c吗?
在下列直角三角形中不能求解的是( )
A.已知一直角边一锐角
B.已知一斜边一锐角
C.已知两边
D.已知两角
D
【跟踪训练】
1.解直角三角形的关键是找到与已知和未知相关联的直角三角形,当图形中没有直角三角形时,要通过作辅助线构造直角三角形(作某边上的高是常用的辅助线).
2.一些解直角三角形的问题往往与其他知识联系,所以要形成知识结构,要把解直角三角形作为一种工具,能在解决各种数学问题时合理运用.
1.(广东·中考)如图,已知Rt△ABC中,斜边BC上的高
AD=4,cosB= ,则AC=____________。
【解析】因为∠BAC=90°,AD是斜边BC上的高,所以
∠B=∠CAD;因为cosB= ,所以在Rt△ADC中,
cos∠CAD= =cosB= ,又因为AD=4,所以AC=5.
答案:5
A
B
C
D
2.(重庆·中考)已知:如图,在Rt△ABC中∠C=90°, .点D为BC边上一点且BD=2AD, ∠ADC=60°,求△ABC的周长.(结果保留根号)
在Rt△ADC中
∵
,∴
∴
在Rt △ABC中
∴
的周长
∵
∴
【解析】
.
.
.
,
,
,
.
3.已知Rt△ABC中,∠C=90°,根据下列条件解直角三角形.
(1)b=5,∠A=30°;(2)
解:(1)∠B=90 –30 =60 .
(2)
∴∠A=30 ,∠B=60 .
由 ,得
4.在Rt△ABC中,∠C=90°,AB=15,
求△ABC的周长和tanA的值.
解:在Rt△ABC中,∠C=90°,AB=15,
∴△ABC的周长为36,
5.(嘉兴·中考)设计建造一条道路,路基的横断面为梯
形ABCD,如图(单位:m).设路基高为h,两侧与水平面
的夹角分别为α和β.已知 h=2,α=45°,CD=10,
(1)求路基底部AB的宽.
(2)修筑这样的路基1 000m,需要多少土石方?
在Rt△ADE中,∵
在Rt△CFB中,∵
∴
在梯形ABCD中,又∵EF=CD=10,
∴AB=AE+EF+FB=16(m).
(2)在梯形ABCD中,∵AB=16,
∴修筑1 000m路基,需要土石方:
于F ,
于E,则
【解析】(1)作
∴面积为
(m ),
人生伟业的建立 ,不在能知,而在能行。
同课章节目录
- 第1章 图形的相似
- 1.1 相似多边形
- 1.2 怎样判定三角形相似
- 1.3 相似三角形的性质
- 1.4 图形的位似
- 第2章 解直角三角形
- 2.1 锐角三角比
- 2.2 30°,45°,60°角的三角比
- 2.3 用计算器求锐角三角比
- 2.4 解直角三角形
- 2.5 解直角三角形的应用
- 第3章 对圆的进一步认识
- 3.1 圆的对称性
- 3.2 确定圆的条件
- 3.3 圆周角
- 3.4 直线与圆的位置关系
- 3.5 三角形的内切圆
- 3.6 弧长及扇形面积的计算
- 3.7 正多边形与圆
- 课题学习 图形变换与图案设计
- 第4章 一元二次方程
- 4.1 一元二次方程
- 4.2 用配方法解一元二次方程
- 4.3 用公式法解一元二次方程
- 4.4 用因式分解法解一元二次方程
- 4.5 一元二次方程的应用
- 4.6 一元二次方程根与系数的关系
