2.5 解直角三角形的应用 第1课时 课件(共23张PPT) 2024-2025学年数学青岛版九年级上册
文档属性
| 名称 | 2.5 解直角三角形的应用 第1课时 课件(共23张PPT) 2024-2025学年数学青岛版九年级上册 |
|
|
| 格式 | ppt | ||
| 文件大小 | 963.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-17 16:22:34 | ||
图片预览






文档简介
(共23张PPT)
2.5 解直角三角形的应用
第1课时
A
B
C
c
b
a
┌
如图,一塔的周围有池塘,无法
到达底部, 你能计算这座塔水
面以上的高度吗?
如图所示是一辆自行车的侧面示意图.已知车轮直径
为65cm,车架中AC的长为42cm,座杆AE的长为18cm,
点E、A、C在同一条直线上,后轴轴心B与中轴轴心C所
在直线BC与地面平行,∠ACB=73°.求车座E到地面
的距离EF(精确到1cm).(参考数据:sin73°≈0.96,
cos73°≈0.29,tan73°≈3.27.)
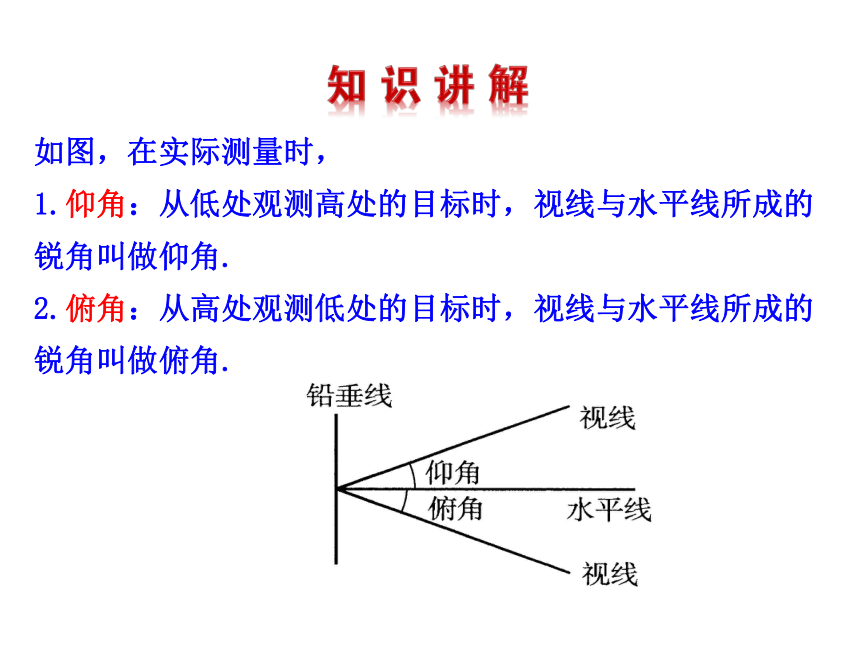
三边关系: a2+b2=c2
两锐角关系:∠A+∠B=∠C
直角三角形的边、角关系
c
a
b
A
B
C
边角关系: sinA=
cosA=
tanA=
【温故知新】
1.明确仰角、俯角的概念,并能将其灵活应用于实际生活.
2.能从实际问题中抽象出几何模型,并能借助计算器解决问题.
3.运用三角比的有关知识来解决实际应用问题.
如图,在实际测量时, 1.仰角:从低处观测高处的目标时,视线与水平线所成的 锐角叫做仰角. 2.俯角:从高处观测低处的目标时,视线与水平线所成的 锐角叫做俯角.
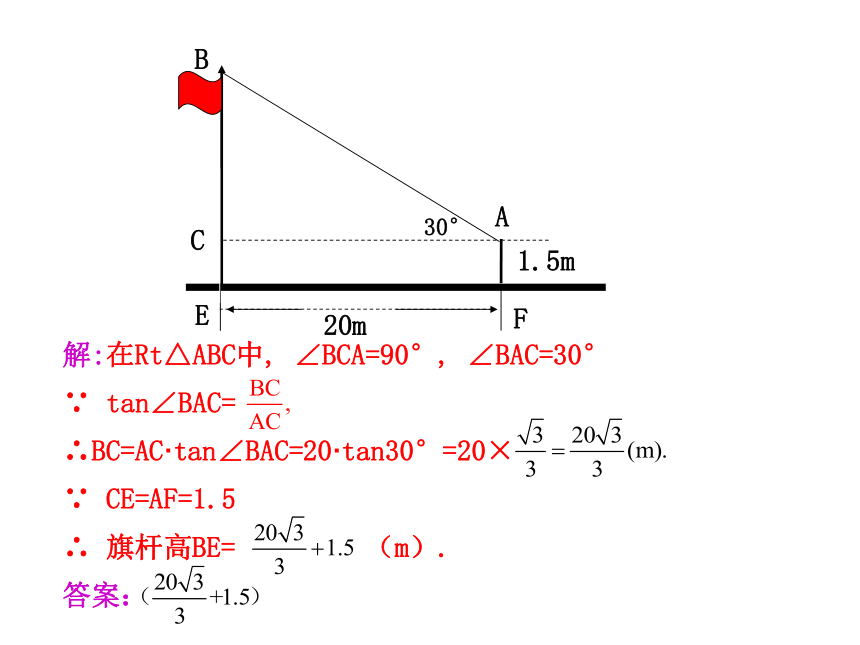
例1 升国旗时,某同学站在离旗杆底部20m处行注目礼,当国旗升至旗杆顶端时,该同学视线的仰角为30°,若双
眼离地面1.5m,则旗杆高度为 m(用含根号的式子来表示).
30°
1.5m
20m
B
E
F
C
A
【例题】
解:在Rt△ABC中, ∠BCA=90°, ∠BAC=30°
∵ tan∠BAC=
∴BC=AC·tan∠BAC=20·tan30°=20×
∵ CE=AF=1.5
∴ 旗杆高BE= (m).
答案:
1.5m
A
30°
20m
B
C
E
F
解:在Rt△ABC中,
A
a
︶
1200m
16°31′
答:飞机从A到控制点B的距离约为4221m.
B
C
例2 如图,某飞机于空中A处探测到目标C,此时飞行高
度AC=1 200m,从飞机上看地面控制点B的俯角α
=16°31′,求飞机从A到控制点B的距离(精确到1m).
分析:由题意,△ABC 是直角三角形,
其中∠C =90°,∠A= 71°34',
∠A所对的边BC=2400m,求 AC.
北
东
一艘帆船航行到B处时,灯塔A在船的北偏东71°34′的方
向,帆船从B处继续向正东方向航行2400m到达C处,此时灯
塔A在船的正北方向.求C处和灯塔A的距离(精确到1m).
A
C
71 34'
B
【跟踪训练】
例3 两幢大楼相距110m,从甲楼顶部看乙楼顶部的仰角为26°,如果甲楼高35m,那么乙楼的高为多少米?(精确到1m,tan26°=0.4877)
A
B
甲楼
乙楼
35
110
26°
C
110
D
E
解:如图,依题意可知:AD=CE=35,AC=DE=110,
∠BAC=26°,在Rt△ABC中,
【例题】
如图,为了测量电线杆的高度AB,在离电线杆22.7m的C处,用高1.20m的测角仪CD测得电线杆顶端B的仰角α=22°,求电线杆AB的高.(精确到0.1 m)
1.20
22.7
=22°
【跟踪训练】
答案:10.37
利用解直角三角形的知识解决实际问题的一般过程是:
1.将实际问题抽象为数学问题;
(画出平面图形,转化为解直角三角形的问题)
2.根据条件的特点,适当选用锐角三角比去解直角三角形;
3.得到数学问题的答案;
4.得到实际问题的答案.
【归纳升华】
通过本课时的学习,需要我们掌握:
1.直角三角形的边角关系,根据已知条件,能灵活相互表示.
2.通过构造直角三角形,运用三角比解决实际问题.
1.如图,某地修建高速公路,要从B地向C地修一座隧
道(B、C在同一水平面上),为了测量B、C两地之间
的距离,某工程队乘坐热气球从C地出发垂直上升100m
到达A处,在A处观察B地的俯角为30 ,则BC两地间的
距离为__________m.
2.从一栋二层楼的楼顶点A处看对面的教学楼,探测器
显示,看到教学楼底部点C处的俯角为45°,看到楼顶
部点D处的仰角为60°,已知两栋楼之间的水平距离为
6米,则教学楼的高CD是__________米.
3.(孝感·中考)如图,一艘船向正北航行,在A处看到灯塔S在船的北偏东30°的方向上,航行12n mile到达B点,在B处看到灯塔S在船的北偏东60°的方向上,此船继续沿正北方向航行过程中距灯塔S的最近距离是 n mile(不作近似计算).
答案:
(参考数据:
)
4.小明家所在居民楼的对面有一座大厦AB,AB=80m.为测量这座居民楼与大厦之间的距离,小明从自己家的窗户C处测得大厦顶部A的仰角为37°,大厦底部B的俯角为48°.求小明家所在居民楼与大厦的距离CD的长度.(结果保留整数)
∵AD+BD = AB,
∴
【解析】设CD =x m.在Rt△ACD中,
则
在Rt△BCD中,tan48°=
解得:x≈43.
答:小明家所在居民楼与大厦的距离CD大约是43m.
则
5. 如图,一艘舰艇在海面下500米A点处测得俯角为30°前下方的海底C 处有黑匣子信号发出,继续在同一深度直线航行4000米后再次在B点处测得俯角为60°前下方的海底C处有黑匣子信号发出,求海底黑匣子C点距离海面的深度(结果保留根号).
【解】作CF⊥AB于点F,则
∴
∵
∴
∴
∴海底黑匣子C点距离海面的深度
【规律方法】根据实际情况,选择测量方法,画出几何图形,构造直角三角形,灵活运用三角比的定义并结合勾股定理的有关知识是进行解题的关键.
一个人最大的破产是绝望,最大的资产是希望。
2.5 解直角三角形的应用
第1课时
A
B
C
c
b
a
┌
如图,一塔的周围有池塘,无法
到达底部, 你能计算这座塔水
面以上的高度吗?
如图所示是一辆自行车的侧面示意图.已知车轮直径
为65cm,车架中AC的长为42cm,座杆AE的长为18cm,
点E、A、C在同一条直线上,后轴轴心B与中轴轴心C所
在直线BC与地面平行,∠ACB=73°.求车座E到地面
的距离EF(精确到1cm).(参考数据:sin73°≈0.96,
cos73°≈0.29,tan73°≈3.27.)
三边关系: a2+b2=c2
两锐角关系:∠A+∠B=∠C
直角三角形的边、角关系
c
a
b
A
B
C
边角关系: sinA=
cosA=
tanA=
【温故知新】
1.明确仰角、俯角的概念,并能将其灵活应用于实际生活.
2.能从实际问题中抽象出几何模型,并能借助计算器解决问题.
3.运用三角比的有关知识来解决实际应用问题.
如图,在实际测量时, 1.仰角:从低处观测高处的目标时,视线与水平线所成的 锐角叫做仰角. 2.俯角:从高处观测低处的目标时,视线与水平线所成的 锐角叫做俯角.
例1 升国旗时,某同学站在离旗杆底部20m处行注目礼,当国旗升至旗杆顶端时,该同学视线的仰角为30°,若双
眼离地面1.5m,则旗杆高度为 m(用含根号的式子来表示).
30°
1.5m
20m
B
E
F
C
A
【例题】
解:在Rt△ABC中, ∠BCA=90°, ∠BAC=30°
∵ tan∠BAC=
∴BC=AC·tan∠BAC=20·tan30°=20×
∵ CE=AF=1.5
∴ 旗杆高BE= (m).
答案:
1.5m
A
30°
20m
B
C
E
F
解:在Rt△ABC中,
A
a
︶
1200m
16°31′
答:飞机从A到控制点B的距离约为4221m.
B
C
例2 如图,某飞机于空中A处探测到目标C,此时飞行高
度AC=1 200m,从飞机上看地面控制点B的俯角α
=16°31′,求飞机从A到控制点B的距离(精确到1m).
分析:由题意,△ABC 是直角三角形,
其中∠C =90°,∠A= 71°34',
∠A所对的边BC=2400m,求 AC.
北
东
一艘帆船航行到B处时,灯塔A在船的北偏东71°34′的方
向,帆船从B处继续向正东方向航行2400m到达C处,此时灯
塔A在船的正北方向.求C处和灯塔A的距离(精确到1m).
A
C
71 34'
B
【跟踪训练】
例3 两幢大楼相距110m,从甲楼顶部看乙楼顶部的仰角为26°,如果甲楼高35m,那么乙楼的高为多少米?(精确到1m,tan26°=0.4877)
A
B
甲楼
乙楼
35
110
26°
C
110
D
E
解:如图,依题意可知:AD=CE=35,AC=DE=110,
∠BAC=26°,在Rt△ABC中,
【例题】
如图,为了测量电线杆的高度AB,在离电线杆22.7m的C处,用高1.20m的测角仪CD测得电线杆顶端B的仰角α=22°,求电线杆AB的高.(精确到0.1 m)
1.20
22.7
=22°
【跟踪训练】
答案:10.37
利用解直角三角形的知识解决实际问题的一般过程是:
1.将实际问题抽象为数学问题;
(画出平面图形,转化为解直角三角形的问题)
2.根据条件的特点,适当选用锐角三角比去解直角三角形;
3.得到数学问题的答案;
4.得到实际问题的答案.
【归纳升华】
通过本课时的学习,需要我们掌握:
1.直角三角形的边角关系,根据已知条件,能灵活相互表示.
2.通过构造直角三角形,运用三角比解决实际问题.
1.如图,某地修建高速公路,要从B地向C地修一座隧
道(B、C在同一水平面上),为了测量B、C两地之间
的距离,某工程队乘坐热气球从C地出发垂直上升100m
到达A处,在A处观察B地的俯角为30 ,则BC两地间的
距离为__________m.
2.从一栋二层楼的楼顶点A处看对面的教学楼,探测器
显示,看到教学楼底部点C处的俯角为45°,看到楼顶
部点D处的仰角为60°,已知两栋楼之间的水平距离为
6米,则教学楼的高CD是__________米.
3.(孝感·中考)如图,一艘船向正北航行,在A处看到灯塔S在船的北偏东30°的方向上,航行12n mile到达B点,在B处看到灯塔S在船的北偏东60°的方向上,此船继续沿正北方向航行过程中距灯塔S的最近距离是 n mile(不作近似计算).
答案:
(参考数据:
)
4.小明家所在居民楼的对面有一座大厦AB,AB=80m.为测量这座居民楼与大厦之间的距离,小明从自己家的窗户C处测得大厦顶部A的仰角为37°,大厦底部B的俯角为48°.求小明家所在居民楼与大厦的距离CD的长度.(结果保留整数)
∵AD+BD = AB,
∴
【解析】设CD =x m.在Rt△ACD中,
则
在Rt△BCD中,tan48°=
解得:x≈43.
答:小明家所在居民楼与大厦的距离CD大约是43m.
则
5. 如图,一艘舰艇在海面下500米A点处测得俯角为30°前下方的海底C 处有黑匣子信号发出,继续在同一深度直线航行4000米后再次在B点处测得俯角为60°前下方的海底C处有黑匣子信号发出,求海底黑匣子C点距离海面的深度(结果保留根号).
【解】作CF⊥AB于点F,则
∴
∵
∴
∴
∴海底黑匣子C点距离海面的深度
【规律方法】根据实际情况,选择测量方法,画出几何图形,构造直角三角形,灵活运用三角比的定义并结合勾股定理的有关知识是进行解题的关键.
一个人最大的破产是绝望,最大的资产是希望。
同课章节目录
- 第1章 图形的相似
- 1.1 相似多边形
- 1.2 怎样判定三角形相似
- 1.3 相似三角形的性质
- 1.4 图形的位似
- 第2章 解直角三角形
- 2.1 锐角三角比
- 2.2 30°,45°,60°角的三角比
- 2.3 用计算器求锐角三角比
- 2.4 解直角三角形
- 2.5 解直角三角形的应用
- 第3章 对圆的进一步认识
- 3.1 圆的对称性
- 3.2 确定圆的条件
- 3.3 圆周角
- 3.4 直线与圆的位置关系
- 3.5 三角形的内切圆
- 3.6 弧长及扇形面积的计算
- 3.7 正多边形与圆
- 课题学习 图形变换与图案设计
- 第4章 一元二次方程
- 4.1 一元二次方程
- 4.2 用配方法解一元二次方程
- 4.3 用公式法解一元二次方程
- 4.4 用因式分解法解一元二次方程
- 4.5 一元二次方程的应用
- 4.6 一元二次方程根与系数的关系
