3.1 圆的对称性 第1课时 课件(共19张PPT) 2024-2025学年数学青岛版九年级上册
文档属性
| 名称 | 3.1 圆的对称性 第1课时 课件(共19张PPT) 2024-2025学年数学青岛版九年级上册 |

|
|
| 格式 | ppt | ||
| 文件大小 | 817.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-17 00:00:00 | ||
图片预览




文档简介
(共19张PPT)
第3章 对圆的进一步认识
3.1 圆的对称性
第1课时
问题:你知道赵州桥吗?它是1 300多年前我国
隋代建造的石拱桥,是我国古代人民勤劳与智慧的结晶,它的主桥拱是圆弧形,它的跨度(弧所对的弦的长)为37.4 m,拱高(弧的中点到弦的距离)为7.2 m,你能求出赵州桥主桥拱的半径吗?
1.理解圆的轴对称性及垂径定理的推导过程;能初
步应用垂径定理进行计算和证明.
2.进一步培养学生观察问题、分析问题和解决问题
的能力.
3.通过圆的对称性,培养学生的数学审美观,并
激发学生对数学的热爱.
想一想:将一个圆沿着任一条直径对折,两侧半圆会有什么关系?
【解析】圆是轴对称图形,任何一条直径所在的直线都是它的对称轴,所以折叠后两侧半圆重叠.
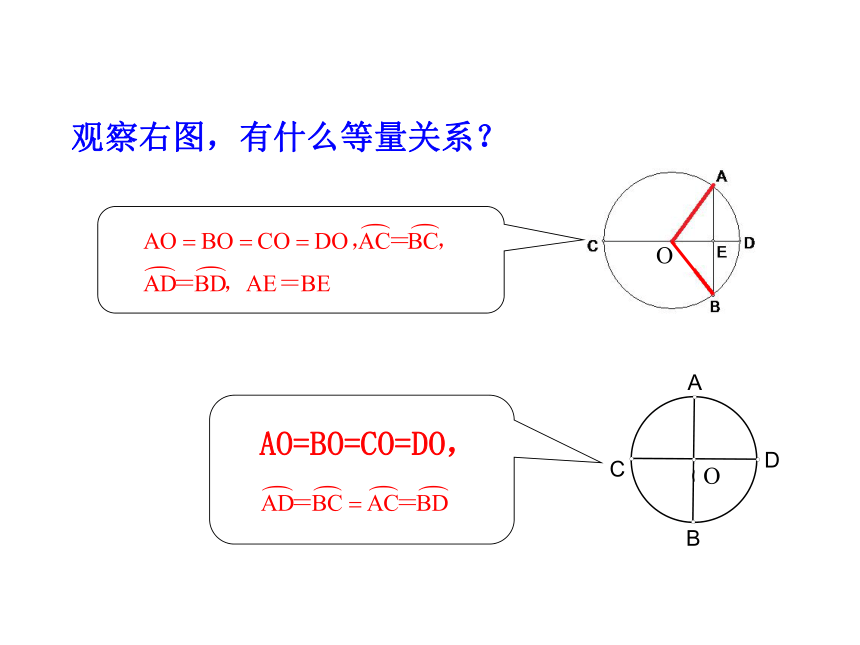
观察右图,有什么等量关系?
AO=BO=CO=DO,
O
O
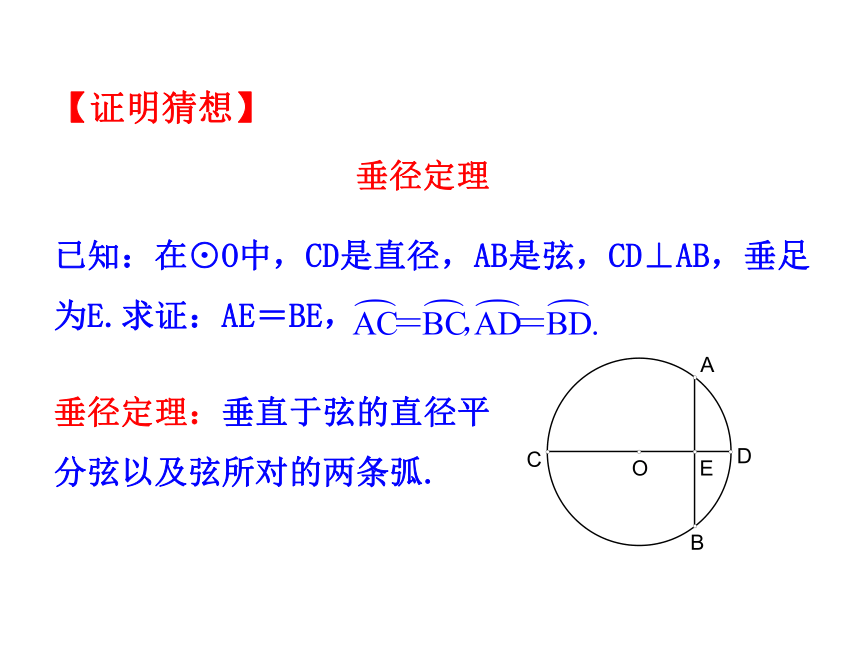
已知:在⊙O中,CD是直径,AB是弦,CD⊥AB,垂足
为E.求证:AE=BE,
垂径定理:垂直于弦的直径平分弦以及弦所对的两条弧.
垂径定理
【证明猜想】
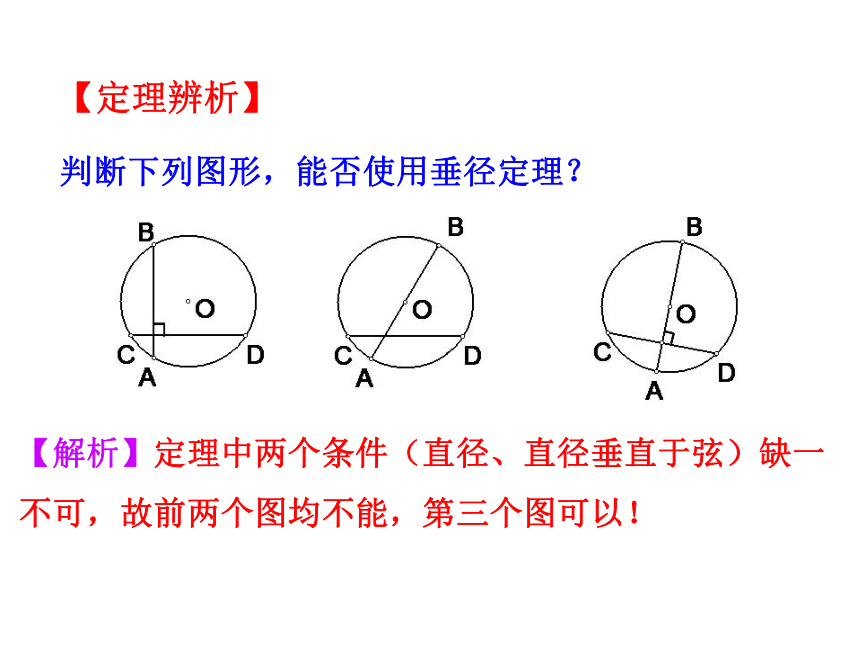
判断下列图形,能否使用垂径定理?
【解析】定理中两个条件(直径、直径垂直于弦)缺一不可,故前两个图均不能,第三个图可以!
【定理辨析】
例 如图,已知在圆O中,弦AB的
长为8 ㎝,圆心O到AB的距离为3 ㎝,
求圆O的半径.
E
O
A
B
【解析】根据题意得,
OE⊥AB,AE=4 cm,OE=3 cm,
在Rt△OEA中,根据勾股定理得:
AO2=OE2+AE2=32+42=25,
AO=5cm.
【例题】
变式1:AC,BD有什么关系?
变式2:AC=BD依然成立吗?
变式3:EA=____, EC=_____.
FD
FB
变式4:______ AC=BD.
OA=OB
变式5:______ AC=BD.
OC=OD
如图,P为⊙O的弦BA延长线上一点,PA=AB=2,PO=5,求⊙O的半径.
M
P
B
O
关于弦的问题,常常需要过圆心作弦的垂线段,这是一条非常重要的辅助线.
【解析】提示作OM 垂直于PB ,连接OA.
答案:
A
【跟踪训练】
画图叙述垂径定理,并说出定理的题设和结论.
题设
结论
①直线CD经过圆心O
②直线CD垂直弦AB
③直线CD平分弦AB
④直线CD平分
⑤直线CD平分
想一想:如果将题设和结论中的5个条件适当互换,情况会怎样?
② ③
① ④⑤
① ④
②③⑤
②④
① ③ ⑤
①②⑤
①②④
④⑤
①②③
③④
③⑤
(1)平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧;
(2)弦的垂直平分线经过圆心,并且平分弦所对的两条弧;
(3)平分弦所对的一条弧的直径,垂直平分弦并且平分弦所对的另一条弧.
【推论1】
如图,CD为⊙O的直径,AB⊥CD,EF⊥CD,你能得到什么结论?
圆的两条平行弦所夹的弧相等.
F
O
B
A
E
C
D
【推论2】
通过本课时的学习,需要我们:
1.理解圆的轴对称性及垂径定理的推证过程;
能初步应用垂径定理进行计算和证明.
2.掌握垂径定理的推论,明确理解“知二得三”
的意义.利用垂径定理及其推论解决相应的数学问题.
2.(湖州·中考)如图,已知⊙O的直径AB⊥弦CD于
点E,下列结论中一定正确的是( )
A.AE=OE B.CE=DE
CE
C.OE=
D.∠AOC=60°
B
1.(绍兴·中考)已知⊙O的半径为5,弦AB的弦心
距为3,则AB的长是( )
A.3 B.4 C.6 D.8
D
3.(安徽·中考)如图,⊙O过点B,C.圆心O在等腰
直角△ABC的内部,∠BAC=90°,OA=1,BC=6,则
⊙O的半径为( )
A. B. C. D.
【解析】选D.延长AO交BC于点D,连接OB,
根据对称性知AO⊥BC,则BD=DC=3.
又△ABC为等腰直角三角形,∠BAC=90°,
则AD= =3,∴OD=3-1=2,
∴OB=
【解析】连接OB,则OB=5,OD=4,利用勾股定理求得BD=3,因为OC⊥AB于点D,所以AD=BD=3,所以AB=6.
答案:6
4.(毕节·中考)如图,AB为⊙O的弦,⊙O的半径为
5,OC⊥AB于点D,交⊙O于点C,且CD=l,则弦AB的
长是 .
5.已知:如图,在以O为圆心
的两个同心圆中,大圆的弦AB
交小圆于C,D两点.
求证:AC=BD.
证明:过O作OE⊥AB,垂足为E,
则AE=BE,CE=DE.
AE-CE=BE-DE.
所以,AC=BD
E
.
A
C
D
B
O
要利用时间,思考一下一天之中做了些什么,是 “正号”还是“负号”,倘若是“正号”,则进步;倘若是“负号”,就得吸取教训,采取措施。
——季米特洛夫
第3章 对圆的进一步认识
3.1 圆的对称性
第1课时
问题:你知道赵州桥吗?它是1 300多年前我国
隋代建造的石拱桥,是我国古代人民勤劳与智慧的结晶,它的主桥拱是圆弧形,它的跨度(弧所对的弦的长)为37.4 m,拱高(弧的中点到弦的距离)为7.2 m,你能求出赵州桥主桥拱的半径吗?
1.理解圆的轴对称性及垂径定理的推导过程;能初
步应用垂径定理进行计算和证明.
2.进一步培养学生观察问题、分析问题和解决问题
的能力.
3.通过圆的对称性,培养学生的数学审美观,并
激发学生对数学的热爱.
想一想:将一个圆沿着任一条直径对折,两侧半圆会有什么关系?
【解析】圆是轴对称图形,任何一条直径所在的直线都是它的对称轴,所以折叠后两侧半圆重叠.
观察右图,有什么等量关系?
AO=BO=CO=DO,
O
O
已知:在⊙O中,CD是直径,AB是弦,CD⊥AB,垂足
为E.求证:AE=BE,
垂径定理:垂直于弦的直径平分弦以及弦所对的两条弧.
垂径定理
【证明猜想】
判断下列图形,能否使用垂径定理?
【解析】定理中两个条件(直径、直径垂直于弦)缺一不可,故前两个图均不能,第三个图可以!
【定理辨析】
例 如图,已知在圆O中,弦AB的
长为8 ㎝,圆心O到AB的距离为3 ㎝,
求圆O的半径.
E
O
A
B
【解析】根据题意得,
OE⊥AB,AE=4 cm,OE=3 cm,
在Rt△OEA中,根据勾股定理得:
AO2=OE2+AE2=32+42=25,
AO=5cm.
【例题】
变式1:AC,BD有什么关系?
变式2:AC=BD依然成立吗?
变式3:EA=____, EC=_____.
FD
FB
变式4:______ AC=BD.
OA=OB
变式5:______ AC=BD.
OC=OD
如图,P为⊙O的弦BA延长线上一点,PA=AB=2,PO=5,求⊙O的半径.
M
P
B
O
关于弦的问题,常常需要过圆心作弦的垂线段,这是一条非常重要的辅助线.
【解析】提示作OM 垂直于PB ,连接OA.
答案:
A
【跟踪训练】
画图叙述垂径定理,并说出定理的题设和结论.
题设
结论
①直线CD经过圆心O
②直线CD垂直弦AB
③直线CD平分弦AB
④直线CD平分
⑤直线CD平分
想一想:如果将题设和结论中的5个条件适当互换,情况会怎样?
② ③
① ④⑤
① ④
②③⑤
②④
① ③ ⑤
①②⑤
①②④
④⑤
①②③
③④
③⑤
(1)平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧;
(2)弦的垂直平分线经过圆心,并且平分弦所对的两条弧;
(3)平分弦所对的一条弧的直径,垂直平分弦并且平分弦所对的另一条弧.
【推论1】
如图,CD为⊙O的直径,AB⊥CD,EF⊥CD,你能得到什么结论?
圆的两条平行弦所夹的弧相等.
F
O
B
A
E
C
D
【推论2】
通过本课时的学习,需要我们:
1.理解圆的轴对称性及垂径定理的推证过程;
能初步应用垂径定理进行计算和证明.
2.掌握垂径定理的推论,明确理解“知二得三”
的意义.利用垂径定理及其推论解决相应的数学问题.
2.(湖州·中考)如图,已知⊙O的直径AB⊥弦CD于
点E,下列结论中一定正确的是( )
A.AE=OE B.CE=DE
CE
C.OE=
D.∠AOC=60°
B
1.(绍兴·中考)已知⊙O的半径为5,弦AB的弦心
距为3,则AB的长是( )
A.3 B.4 C.6 D.8
D
3.(安徽·中考)如图,⊙O过点B,C.圆心O在等腰
直角△ABC的内部,∠BAC=90°,OA=1,BC=6,则
⊙O的半径为( )
A. B. C. D.
【解析】选D.延长AO交BC于点D,连接OB,
根据对称性知AO⊥BC,则BD=DC=3.
又△ABC为等腰直角三角形,∠BAC=90°,
则AD= =3,∴OD=3-1=2,
∴OB=
【解析】连接OB,则OB=5,OD=4,利用勾股定理求得BD=3,因为OC⊥AB于点D,所以AD=BD=3,所以AB=6.
答案:6
4.(毕节·中考)如图,AB为⊙O的弦,⊙O的半径为
5,OC⊥AB于点D,交⊙O于点C,且CD=l,则弦AB的
长是 .
5.已知:如图,在以O为圆心
的两个同心圆中,大圆的弦AB
交小圆于C,D两点.
求证:AC=BD.
证明:过O作OE⊥AB,垂足为E,
则AE=BE,CE=DE.
AE-CE=BE-DE.
所以,AC=BD
E
.
A
C
D
B
O
要利用时间,思考一下一天之中做了些什么,是 “正号”还是“负号”,倘若是“正号”,则进步;倘若是“负号”,就得吸取教训,采取措施。
——季米特洛夫
同课章节目录
- 第1章 图形的相似
- 1.1 相似多边形
- 1.2 怎样判定三角形相似
- 1.3 相似三角形的性质
- 1.4 图形的位似
- 第2章 解直角三角形
- 2.1 锐角三角比
- 2.2 30°,45°,60°角的三角比
- 2.3 用计算器求锐角三角比
- 2.4 解直角三角形
- 2.5 解直角三角形的应用
- 第3章 对圆的进一步认识
- 3.1 圆的对称性
- 3.2 确定圆的条件
- 3.3 圆周角
- 3.4 直线与圆的位置关系
- 3.5 三角形的内切圆
- 3.6 弧长及扇形面积的计算
- 3.7 正多边形与圆
- 课题学习 图形变换与图案设计
- 第4章 一元二次方程
- 4.1 一元二次方程
- 4.2 用配方法解一元二次方程
- 4.3 用公式法解一元二次方程
- 4.4 用因式分解法解一元二次方程
- 4.5 一元二次方程的应用
- 4.6 一元二次方程根与系数的关系
