3.3 圆周角 第1课时 课件(共18张PPT) 2024-2025学年数学青岛版九年级上册
文档属性
| 名称 | 3.3 圆周角 第1课时 课件(共18张PPT) 2024-2025学年数学青岛版九年级上册 |
|
|
| 格式 | ppt | ||
| 文件大小 | 822.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-17 16:39:49 | ||
图片预览


文档简介
(共18张PPT)
3.3 圆周角
第1课时
·
O
B
A
圆心角: 顶点在圆心的角
1.经历探索圆周角的有关性质的过程;
2.进一步理解圆周角的概念及其相关性质,并能运用相关性质解决有关问题;
3.体会分类,转化等数学思想方法,学会数学的转化问题.
o
A
B
C
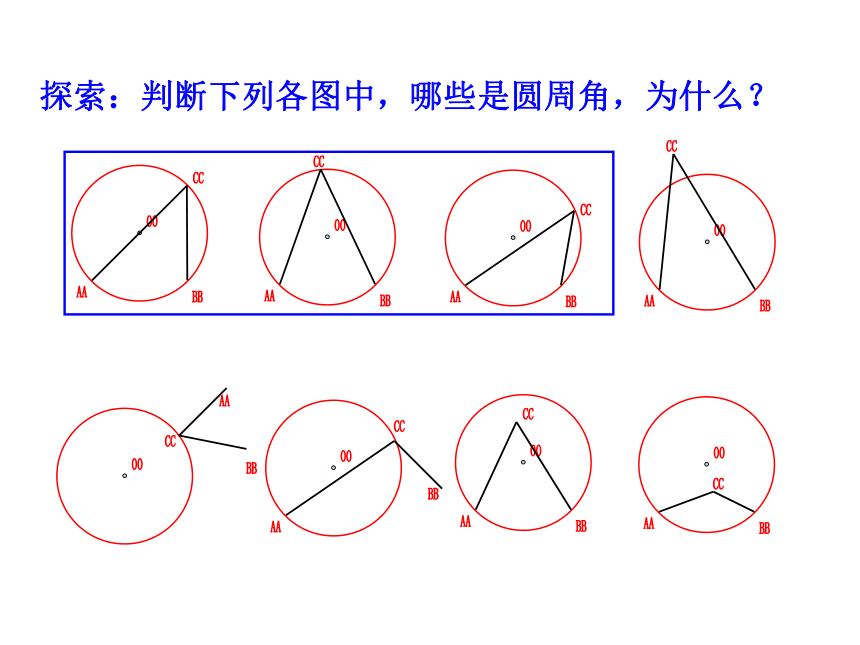
能给图中像∠ACB 这样的角下个定义吗?
顶点在圆上,并且两边在圆内的部分是圆的两条弦,这样的角叫做圆周角.
探索:判断下列各图中,哪些是圆周角,为什么?
o
A
B
o
A
B
o
A
B
o
A
B
o
A
B
o
A
B
C
C
C
C
C
C
o
A
B
C
o
A
B
C
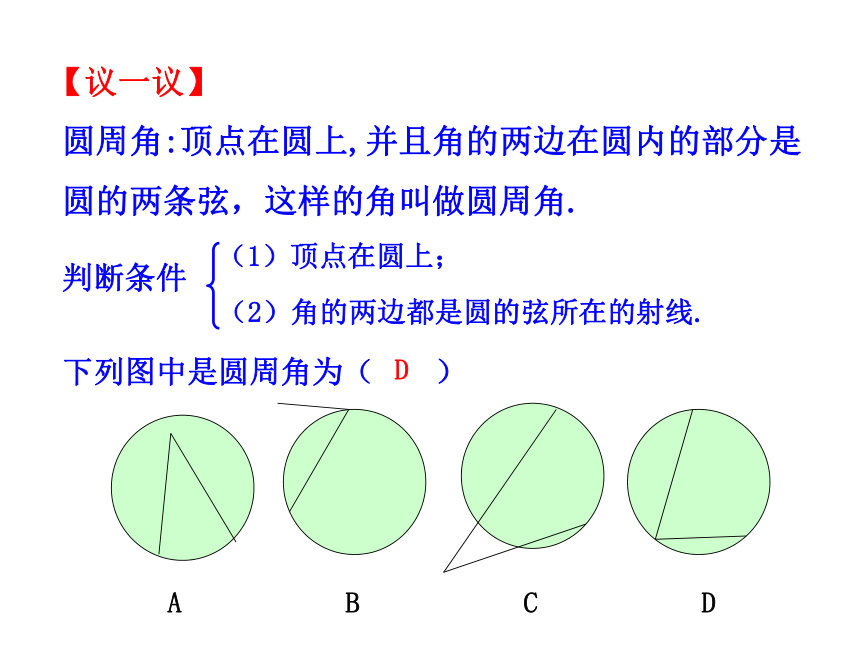
圆周角:顶点在圆上,并且角的两边在圆内的部分是圆的两条弦,这样的角叫做圆周角.
判断条件
(1)顶点在圆上;
(2)角的两边都是圆的弦所在的射线.
下列图中是圆周角为( )
D
C
B
A
D
【议一议】
B
A
C
D
E
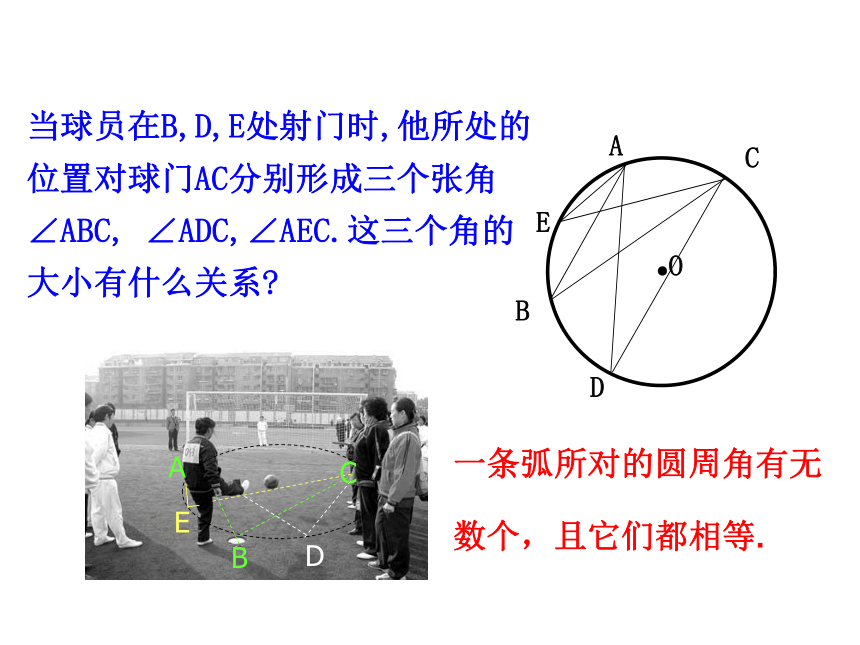
一条弧所对的圆周角有无数个,且它们都相等.
当球员在B,D,E处射门时,他所处的
位置对球门AC分别形成三个张角
∠ABC, ∠ADC,∠AEC.这三个角的
大小有什么关系
●O
B
A
C
D
E
如图,观察圆周角∠ACB与圆心角∠AOB,它们的大小有什么关系
圆周角定理:圆周角等于它所对弧上的圆心角的一半.
∠ACB= ∠AOB
推论1:圆周角的度数等于它所对弧的度数的一半.
●O
A
B
C
●O
A
B
C
●O
A
B
C
(1)在圆周角的
一边上
(2)在圆周角的内部
(3)在圆周角的外部
圆周角定理揭示了同弧所对的圆周角和圆心角的关系
注意圆心与圆周角的位置关系.
【议一议】
●O
C
A
B
1. 当圆心在圆周角的一边上时.
证明:如图,OA=OC ∠A=∠C
又∠BOC=∠A+∠C ∠BOC=2∠A
一条弧所对的圆周角的度数等于它所对的圆心角度数的一半.
2.当圆心在圆周角的内部时
能否转化为1的情况
证明:如图过点A作直径AD.由1可得:
∠BAD = ∠BOD,∠CAD = ∠COD,
∠BAD+ ∠CAD = (∠BOD + ∠COD)
∴ ∠BAC = ∠BOC.
●O
A
B
C
.
.
D
3.当圆心在圆周角的外部时.留为作业.
一条弧所对的圆周角等于它所对的圆心角的一半.
同弧或等弧上的圆周角相等,在同圆或等圆中,相等的圆周角所对的弧相等.
A
B
C
D
E
一条弦所对的圆周角有无数个,顶点在劣弧或优弧上的圆周角分别相等.这条弦两侧的圆周角互补.
如图:弦AB所对圆周角有哪些?
它们有什么关系?
解析:弦AB所对圆周角有∠D, ∠E, ∠C,
∠D=∠E,∠D+∠C=180°,∠E+∠C=180°
【归 纳】
【例 题】
2.如图,在⊙O中,∠BOC=50°,
求∠A的大小.
解析: ∠A = ∠BOC = 25°.
●O
B
A
C
1.如图相等的圆周角有哪些?
解析:∠1= ∠4 , ∠2= ∠8 ,
∠3= ∠6 , ∠5= ∠7
.
A
B
C
D
4
5 6
7 8
1
2
3
【跟踪训练】
1.圆周角性质:圆周角等于它所对弧上圆心角的一半,等于该弧度数的一半.
2.能用圆周角的性质解决有关圆的证明和计算问题.
通过本课时的学习,需要我们掌握:
1.(江津·中考)已知:点A、B、
P为⊙O上的点,若∠PBO=15 ,
且PA∥OB,则∠AOB=( )
A.15 B.20
C.30 D.45
C
2.(宁德·中考)如图,在⊙O中,∠ACB=34°,
则∠AOB的度数是( )
A.17° B.34° C.56° D.68°
A
O
C
B
D
3.(潍坊·中考)如图,AB是⊙O的直径,C、D是⊙O上的两点,且AC=CD.
求证:OC∥BD.
证明: ⊙O中,因为AC=CD,
∴∠ABC=∠DBC,
∵OC=OB,
∴∠ABC=∠OCB,
∴∠OCB=∠DBC,
∴OC∥BD.
生命里最重要的事情是要有个远大的目标,并借才能与坚毅来达成它。
3.3 圆周角
第1课时
·
O
B
A
圆心角: 顶点在圆心的角
1.经历探索圆周角的有关性质的过程;
2.进一步理解圆周角的概念及其相关性质,并能运用相关性质解决有关问题;
3.体会分类,转化等数学思想方法,学会数学的转化问题.
o
A
B
C
能给图中像∠ACB 这样的角下个定义吗?
顶点在圆上,并且两边在圆内的部分是圆的两条弦,这样的角叫做圆周角.
探索:判断下列各图中,哪些是圆周角,为什么?
o
A
B
o
A
B
o
A
B
o
A
B
o
A
B
o
A
B
C
C
C
C
C
C
o
A
B
C
o
A
B
C
圆周角:顶点在圆上,并且角的两边在圆内的部分是圆的两条弦,这样的角叫做圆周角.
判断条件
(1)顶点在圆上;
(2)角的两边都是圆的弦所在的射线.
下列图中是圆周角为( )
D
C
B
A
D
【议一议】
B
A
C
D
E
一条弧所对的圆周角有无数个,且它们都相等.
当球员在B,D,E处射门时,他所处的
位置对球门AC分别形成三个张角
∠ABC, ∠ADC,∠AEC.这三个角的
大小有什么关系
●O
B
A
C
D
E
如图,观察圆周角∠ACB与圆心角∠AOB,它们的大小有什么关系
圆周角定理:圆周角等于它所对弧上的圆心角的一半.
∠ACB= ∠AOB
推论1:圆周角的度数等于它所对弧的度数的一半.
●O
A
B
C
●O
A
B
C
●O
A
B
C
(1)在圆周角的
一边上
(2)在圆周角的内部
(3)在圆周角的外部
圆周角定理揭示了同弧所对的圆周角和圆心角的关系
注意圆心与圆周角的位置关系.
【议一议】
●O
C
A
B
1. 当圆心在圆周角的一边上时.
证明:如图,OA=OC ∠A=∠C
又∠BOC=∠A+∠C ∠BOC=2∠A
一条弧所对的圆周角的度数等于它所对的圆心角度数的一半.
2.当圆心在圆周角的内部时
能否转化为1的情况
证明:如图过点A作直径AD.由1可得:
∠BAD = ∠BOD,∠CAD = ∠COD,
∠BAD+ ∠CAD = (∠BOD + ∠COD)
∴ ∠BAC = ∠BOC.
●O
A
B
C
.
.
D
3.当圆心在圆周角的外部时.留为作业.
一条弧所对的圆周角等于它所对的圆心角的一半.
同弧或等弧上的圆周角相等,在同圆或等圆中,相等的圆周角所对的弧相等.
A
B
C
D
E
一条弦所对的圆周角有无数个,顶点在劣弧或优弧上的圆周角分别相等.这条弦两侧的圆周角互补.
如图:弦AB所对圆周角有哪些?
它们有什么关系?
解析:弦AB所对圆周角有∠D, ∠E, ∠C,
∠D=∠E,∠D+∠C=180°,∠E+∠C=180°
【归 纳】
【例 题】
2.如图,在⊙O中,∠BOC=50°,
求∠A的大小.
解析: ∠A = ∠BOC = 25°.
●O
B
A
C
1.如图相等的圆周角有哪些?
解析:∠1= ∠4 , ∠2= ∠8 ,
∠3= ∠6 , ∠5= ∠7
.
A
B
C
D
4
5 6
7 8
1
2
3
【跟踪训练】
1.圆周角性质:圆周角等于它所对弧上圆心角的一半,等于该弧度数的一半.
2.能用圆周角的性质解决有关圆的证明和计算问题.
通过本课时的学习,需要我们掌握:
1.(江津·中考)已知:点A、B、
P为⊙O上的点,若∠PBO=15 ,
且PA∥OB,则∠AOB=( )
A.15 B.20
C.30 D.45
C
2.(宁德·中考)如图,在⊙O中,∠ACB=34°,
则∠AOB的度数是( )
A.17° B.34° C.56° D.68°
A
O
C
B
D
3.(潍坊·中考)如图,AB是⊙O的直径,C、D是⊙O上的两点,且AC=CD.
求证:OC∥BD.
证明: ⊙O中,因为AC=CD,
∴∠ABC=∠DBC,
∵OC=OB,
∴∠ABC=∠OCB,
∴∠OCB=∠DBC,
∴OC∥BD.
生命里最重要的事情是要有个远大的目标,并借才能与坚毅来达成它。
同课章节目录
- 第1章 图形的相似
- 1.1 相似多边形
- 1.2 怎样判定三角形相似
- 1.3 相似三角形的性质
- 1.4 图形的位似
- 第2章 解直角三角形
- 2.1 锐角三角比
- 2.2 30°,45°,60°角的三角比
- 2.3 用计算器求锐角三角比
- 2.4 解直角三角形
- 2.5 解直角三角形的应用
- 第3章 对圆的进一步认识
- 3.1 圆的对称性
- 3.2 确定圆的条件
- 3.3 圆周角
- 3.4 直线与圆的位置关系
- 3.5 三角形的内切圆
- 3.6 弧长及扇形面积的计算
- 3.7 正多边形与圆
- 课题学习 图形变换与图案设计
- 第4章 一元二次方程
- 4.1 一元二次方程
- 4.2 用配方法解一元二次方程
- 4.3 用公式法解一元二次方程
- 4.4 用因式分解法解一元二次方程
- 4.5 一元二次方程的应用
- 4.6 一元二次方程根与系数的关系
