3.3 圆周角 第2课时 课件(共20张PPT) 2024-2025学年数学青岛版九年级上册
文档属性
| 名称 | 3.3 圆周角 第2课时 课件(共20张PPT) 2024-2025学年数学青岛版九年级上册 |  | |
| 格式 | ppt | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-17 16:44:27 | ||
图片预览




文档简介
(共20张PPT)
3.3 圆周角
第2课时
1.掌握圆周角定理的两个推论,并掌握直径(或半圆)
所对的圆周角是直角及90°的圆周角所对的弦是直径的
性质,并能运用此性质解决问题;
2.经历探索圆周角性质的过程,培养学生分析问题和解
决问题的能力.
3.理解圆内接四边形的性质定理,并能运用定理解决
实际问题.
圆周角定理的推论2:
同弧或等弧上的圆周角相等;在同圆或等圆中,相等的圆周角所对的弧相等.
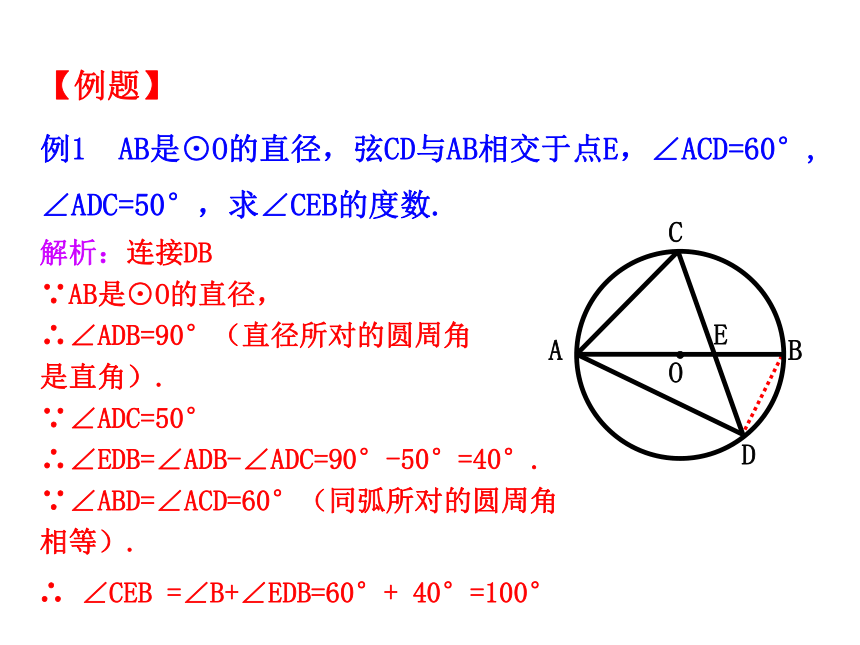
如图,BC是⊙O的直径,它所对的圆周角是锐角、钝角,还是直角?为什么?
∠BAC所对的圆心角是_______
圆周角∠BDC=90°,弦BC经过圆心吗?为什么?
C
A
B
O
D
推论3:直径所对的圆周角是直角,90°的圆周角所对的弦是直径.
180°
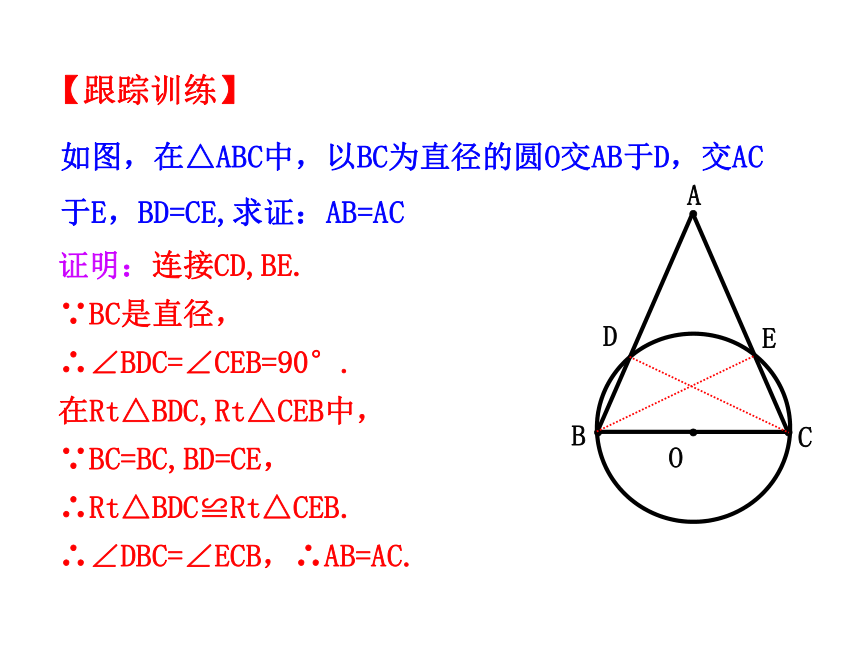
例1 AB是⊙O的直径,弦CD与AB相交于点E,∠ACD=60°,
∠ADC=50°,求∠CEB的度数.
C
D
E
A
B
O
解析:连接DB
∵AB是⊙O的直径,
∴∠ADB=90°(直径所对的圆周角
是直角).
∵∠ADC=50°
∴∠EDB=∠ADB-∠ADC=90°-50°=40°.
∵∠ABD=∠ACD=60°(同弧所对的圆周角相等).
∴ ∠CEB =∠B+∠EDB=60°+ 40°=100°
【例题】
如图,在△ABC中,以BC为直径的圆O交AB于D,交AC于E,BD=CE,求证:AB=AC
证明:连接CD,BE.
∵BC是直径,
∴∠BDC=∠CEB=90°.
在Rt△BDC,Rt△CEB中, ∵BC=BC,BD=CE,
∴Rt△BDC≌Rt△CEB. ∴∠DBC=∠ECB,∴AB=AC.
C
D
A
B
O
E
【跟踪训练】
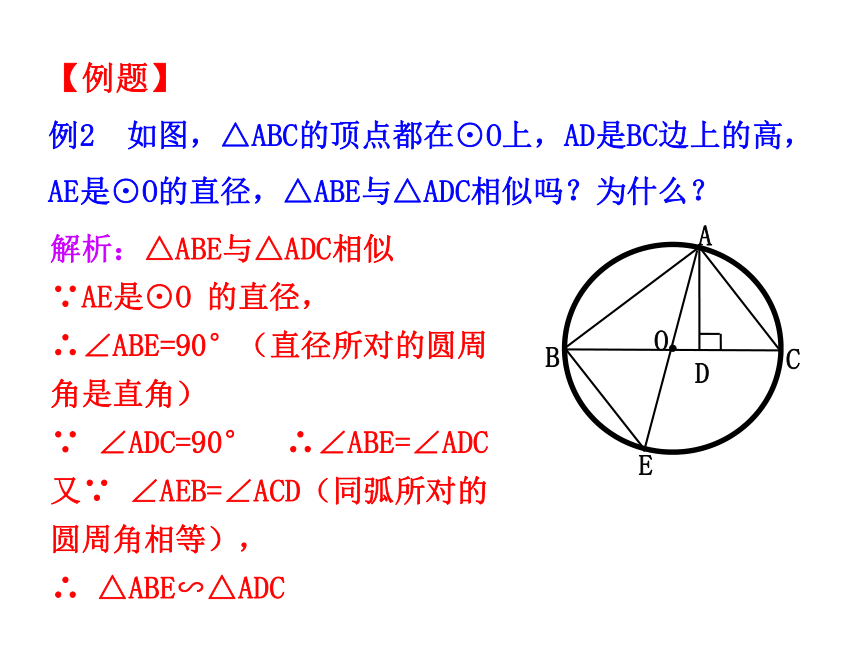
例2 如图,△ABC的顶点都在⊙O上,AD是BC边上的高,AE是⊙O的直径,△ABE与△ADC相似吗?为什么?
E
C
D
A
B
O
解析:△ABE与△ADC相似
∵AE是⊙O 的直径,
∴∠ABE=90°(直径所对的圆周角是直角)
∵ ∠ADC=90° ∴∠ABE=∠ADC
又∵ ∠AEB=∠ACD(同弧所对的圆周角相等),
∴ △ABE∽△ADC
【例题】
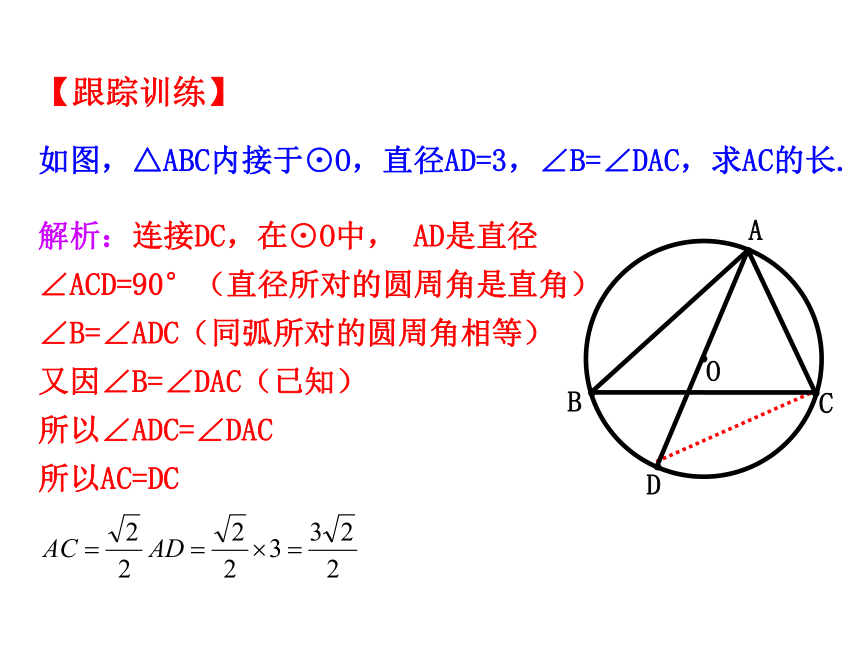
如图,△ABC内接于⊙O,直径AD=3,∠B=∠DAC,求AC的长.
O
D
C
B
A
解析:连接DC,在⊙O中, AD是直径
∠ACD=90°(直径所对的圆周角是直角)
∠B=∠ADC(同弧所对的圆周角相等)
又因∠B=∠DAC(已知)
所以∠ADC=∠DAC
所以AC=DC
【跟踪训练】
【圆内接多边形】
所有顶点都在同一个圆上的多边形叫做圆内接多边形,这个圆叫做这个多边形的外接圆。
·
A
B
O
C
D
圆周角定理的推论4:圆内接四边形的对角互补.
已知:如图,四边形ABCD内接于⊙O,
求证:∠A+∠C=1800,∠B+∠D=1800.
·
A
B
O
C
D
例3 已知:如图,AD是△ABC的外角∠EAC的平分线,与△ABC的外接圆交于点D.求证:DB=DC.
1.圆内接四边形ABCD中,∠A, ∠B, ∠C的度数之比是
1:2:3,则这个四边形最大角的度数是_______.
2.四边形ABCD内接于圆,AD∥BC,
若AD=4,BC=6,则四边形ABCD的面积为_____.
·
A
B
O
C
D
135°
【跟踪训练】
例4 如果要把横截面直径为30cm的圆柱形原木锯成一根横截面为正方形的木材,并使截面尽可能的大,应怎样锯?如果这根原木长15米,问:锯出的木材体积为多少立方米?(树皮等损耗略去不计)
【解析】
1.掌握圆周角定理的两个推论:
推论2:同弧或等弧上的圆周角相等;在同圆或等圆中,相等的圆周角所对的弧相等;
推论3:直径所对的圆周角是直角,90°的圆周角所对的弦是直径.
2.圆内接多边形的相关概念及圆内接四边形的性质.
通过本课时的学习,需要我们掌握:
1.(南通·中考) 如图,⊙O的直径
AB=4,点C在⊙O上,∠ABC=30°,则
AC的长是( )
A.1 B. C. D.2
2.(台州·中考)如图,⊙O的直径
CD⊥AB,∠AOC=50°,则∠CDB大小
为 ( )
A.25° B.30°
C.40° D.50°
A
B
O
C
D
A
D
A
B
C
D
E
o
3.圆内接四边形ABCD中,∠A:∠B:∠C=2:3:4,则
∠A= ,∠B= ,∠C= ,∠D= .
4.如图,四边形ABCD内接于⊙O, ∠DCE=75°,
则∠BOD= .
60°
90°
120°
90°
150°
5.(邵阳·中考)如图,在等边
△ABC中,以AB为直径的⊙O与BC相
交于点D,连接AD,则∠DAC的度数
为 .
A
B
D
C
30°
O
F
D
E
O
C
B
A
M
6.如图,BC是⊙O的直径,AD⊥BC,垂足为D, ,
BF和AD相交于E,
求证:AE=BE
【证明】延长AD与圆相交于M,根据题意,得
∴所对的圆周角相等,即∠BAD=∠ABF,∵E是AD和BF的交点 ∴AE=BE
我们应该有恒心,尤其要有自信心。
——居里夫人
3.3 圆周角
第2课时
1.掌握圆周角定理的两个推论,并掌握直径(或半圆)
所对的圆周角是直角及90°的圆周角所对的弦是直径的
性质,并能运用此性质解决问题;
2.经历探索圆周角性质的过程,培养学生分析问题和解
决问题的能力.
3.理解圆内接四边形的性质定理,并能运用定理解决
实际问题.
圆周角定理的推论2:
同弧或等弧上的圆周角相等;在同圆或等圆中,相等的圆周角所对的弧相等.
如图,BC是⊙O的直径,它所对的圆周角是锐角、钝角,还是直角?为什么?
∠BAC所对的圆心角是_______
圆周角∠BDC=90°,弦BC经过圆心吗?为什么?
C
A
B
O
D
推论3:直径所对的圆周角是直角,90°的圆周角所对的弦是直径.
180°
例1 AB是⊙O的直径,弦CD与AB相交于点E,∠ACD=60°,
∠ADC=50°,求∠CEB的度数.
C
D
E
A
B
O
解析:连接DB
∵AB是⊙O的直径,
∴∠ADB=90°(直径所对的圆周角
是直角).
∵∠ADC=50°
∴∠EDB=∠ADB-∠ADC=90°-50°=40°.
∵∠ABD=∠ACD=60°(同弧所对的圆周角相等).
∴ ∠CEB =∠B+∠EDB=60°+ 40°=100°
【例题】
如图,在△ABC中,以BC为直径的圆O交AB于D,交AC于E,BD=CE,求证:AB=AC
证明:连接CD,BE.
∵BC是直径,
∴∠BDC=∠CEB=90°.
在Rt△BDC,Rt△CEB中, ∵BC=BC,BD=CE,
∴Rt△BDC≌Rt△CEB. ∴∠DBC=∠ECB,∴AB=AC.
C
D
A
B
O
E
【跟踪训练】
例2 如图,△ABC的顶点都在⊙O上,AD是BC边上的高,AE是⊙O的直径,△ABE与△ADC相似吗?为什么?
E
C
D
A
B
O
解析:△ABE与△ADC相似
∵AE是⊙O 的直径,
∴∠ABE=90°(直径所对的圆周角是直角)
∵ ∠ADC=90° ∴∠ABE=∠ADC
又∵ ∠AEB=∠ACD(同弧所对的圆周角相等),
∴ △ABE∽△ADC
【例题】
如图,△ABC内接于⊙O,直径AD=3,∠B=∠DAC,求AC的长.
O
D
C
B
A
解析:连接DC,在⊙O中, AD是直径
∠ACD=90°(直径所对的圆周角是直角)
∠B=∠ADC(同弧所对的圆周角相等)
又因∠B=∠DAC(已知)
所以∠ADC=∠DAC
所以AC=DC
【跟踪训练】
【圆内接多边形】
所有顶点都在同一个圆上的多边形叫做圆内接多边形,这个圆叫做这个多边形的外接圆。
·
A
B
O
C
D
圆周角定理的推论4:圆内接四边形的对角互补.
已知:如图,四边形ABCD内接于⊙O,
求证:∠A+∠C=1800,∠B+∠D=1800.
·
A
B
O
C
D
例3 已知:如图,AD是△ABC的外角∠EAC的平分线,与△ABC的外接圆交于点D.求证:DB=DC.
1.圆内接四边形ABCD中,∠A, ∠B, ∠C的度数之比是
1:2:3,则这个四边形最大角的度数是_______.
2.四边形ABCD内接于圆,AD∥BC,
若AD=4,BC=6,则四边形ABCD的面积为_____.
·
A
B
O
C
D
135°
【跟踪训练】
例4 如果要把横截面直径为30cm的圆柱形原木锯成一根横截面为正方形的木材,并使截面尽可能的大,应怎样锯?如果这根原木长15米,问:锯出的木材体积为多少立方米?(树皮等损耗略去不计)
【解析】
1.掌握圆周角定理的两个推论:
推论2:同弧或等弧上的圆周角相等;在同圆或等圆中,相等的圆周角所对的弧相等;
推论3:直径所对的圆周角是直角,90°的圆周角所对的弦是直径.
2.圆内接多边形的相关概念及圆内接四边形的性质.
通过本课时的学习,需要我们掌握:
1.(南通·中考) 如图,⊙O的直径
AB=4,点C在⊙O上,∠ABC=30°,则
AC的长是( )
A.1 B. C. D.2
2.(台州·中考)如图,⊙O的直径
CD⊥AB,∠AOC=50°,则∠CDB大小
为 ( )
A.25° B.30°
C.40° D.50°
A
B
O
C
D
A
D
A
B
C
D
E
o
3.圆内接四边形ABCD中,∠A:∠B:∠C=2:3:4,则
∠A= ,∠B= ,∠C= ,∠D= .
4.如图,四边形ABCD内接于⊙O, ∠DCE=75°,
则∠BOD= .
60°
90°
120°
90°
150°
5.(邵阳·中考)如图,在等边
△ABC中,以AB为直径的⊙O与BC相
交于点D,连接AD,则∠DAC的度数
为 .
A
B
D
C
30°
O
F
D
E
O
C
B
A
M
6.如图,BC是⊙O的直径,AD⊥BC,垂足为D, ,
BF和AD相交于E,
求证:AE=BE
【证明】延长AD与圆相交于M,根据题意,得
∴所对的圆周角相等,即∠BAD=∠ABF,∵E是AD和BF的交点 ∴AE=BE
我们应该有恒心,尤其要有自信心。
——居里夫人
同课章节目录
- 第1章 图形的相似
- 1.1 相似多边形
- 1.2 怎样判定三角形相似
- 1.3 相似三角形的性质
- 1.4 图形的位似
- 第2章 解直角三角形
- 2.1 锐角三角比
- 2.2 30°,45°,60°角的三角比
- 2.3 用计算器求锐角三角比
- 2.4 解直角三角形
- 2.5 解直角三角形的应用
- 第3章 对圆的进一步认识
- 3.1 圆的对称性
- 3.2 确定圆的条件
- 3.3 圆周角
- 3.4 直线与圆的位置关系
- 3.5 三角形的内切圆
- 3.6 弧长及扇形面积的计算
- 3.7 正多边形与圆
- 课题学习 图形变换与图案设计
- 第4章 一元二次方程
- 4.1 一元二次方程
- 4.2 用配方法解一元二次方程
- 4.3 用公式法解一元二次方程
- 4.4 用因式分解法解一元二次方程
- 4.5 一元二次方程的应用
- 4.6 一元二次方程根与系数的关系
