4.1 一元二次方程 第2课时 课件(共16张PPT) 2024-2025学年数学青岛版九年级上册
文档属性
| 名称 | 4.1 一元二次方程 第2课时 课件(共16张PPT) 2024-2025学年数学青岛版九年级上册 |

|
|
| 格式 | ppt | ||
| 文件大小 | 808.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-17 17:26:49 | ||
图片预览





文档简介
(共16张PPT)
第2课时
4.1 一元二次方程
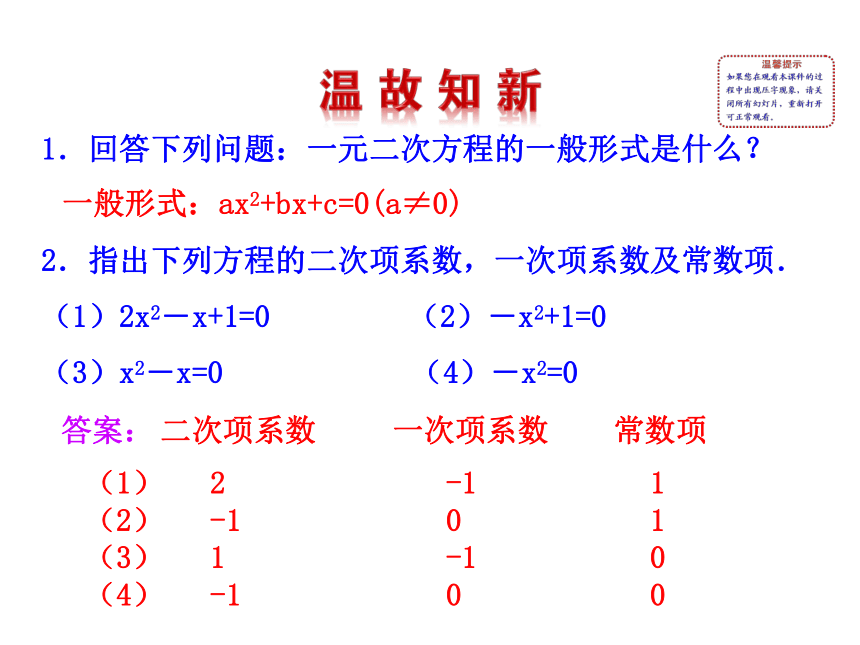
1.回答下列问题:一元二次方程的一般形式是什么?
2.指出下列方程的二次项系数,一次项系数及常数项.
(1)2x2―x+1=0 (2)―x2+1=0
(3)x2―x=0 (4)―x2=0
一般形式:ax2+bx+c=0(a≠0)
答案:
二次项系数
一次项系数
常数项
(1) 2 -1 1
(2) -1 0 1
(3) 1 -1 0
(4) -1 0 0
3.什么叫方程的解,什么叫解方程?
方程的解就是符合方程的未知数的值.
求方程的解的过程叫做解方程.
这节课我们通过估算的方法探索方程的解的大致范围.
1.经历对方程解的探索过程,理解方程解的意义.
2.会估算一元二次方程的解.
1.一块四周镶有宽度相等的花边的地毯如图所示,它的
长为8 m,宽为5 m.如果地毯中央长方形图案的面积为
18m2,则花边多宽
【解析】设花边的宽为x m, 根据题意,可得方程 (8-2x)(5-2x)=18 即:2x2-13x+11=0.
对于方程(8-2x)(5-2x)=18,即2x2-13x+11=0
(1)x可能小于0吗 说说你的理由.
(2)x可能大于4吗 可能大于2.5吗 说说你的理由,并与同伴进行交流.
(3)完成下表:
(4)你知道地毯花边的宽x(m)是多少吗 还有其他求解
方法吗 与同伴进行交流.
x 0 0.5 1 1.5 2 2.5
2x2-13x+11
11
5
0
-4
-7
-9
答案:1m 其他求解方法略
不可能 理由略
不可能 理由略
x
8m
1
10m
7m
6m
【解析】由勾股定理可知,滑动
前梯子底端距墙 m ;
如果设梯子底端滑动x m,那么滑
动后梯子底端距墙 m;
根据题意,可得方程:
72+(x+6)2=102
6
x+6
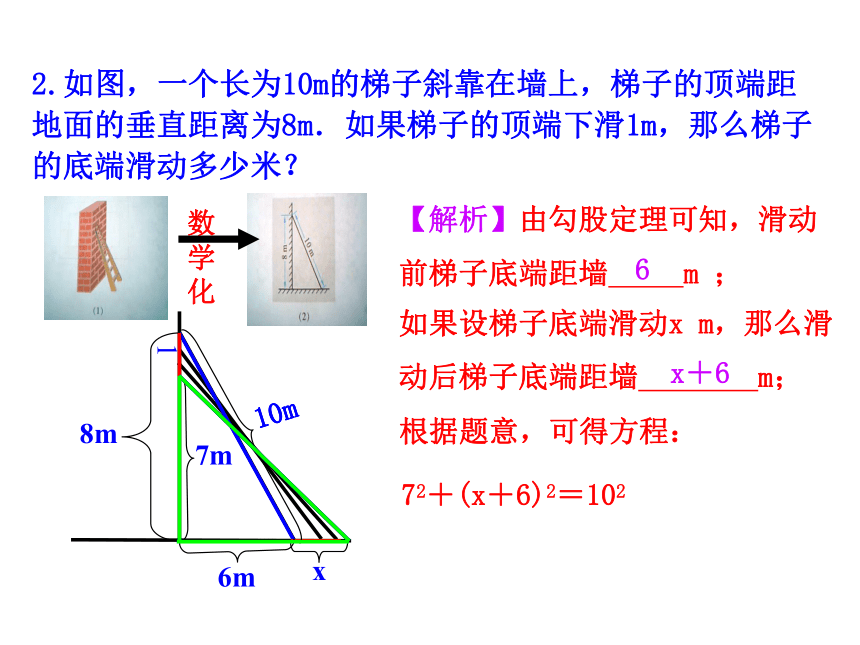
2.如图,一个长为10m的梯子斜靠在墙上,梯子的顶端距地面的垂直距离为8m.如果梯子的顶端下滑1m,那么梯子的底端滑动多少米?
10m
数学化
在这个问题中,梯子底端滑动的距离x(m)满足方程(x+6)2+72=102,把这个方程化为一般形式为x2+12x-15=0 .
(1)小明认为底端也滑动了1m,他的说法正确吗 为什么
(2)底端滑动的距离可能是2m吗 可能是3m吗 为什么
不正确,因为x=1不满足方程.
不可能,因为x=2,3不满足方程.
(3)你能猜出滑动距离x(m)的大致范围吗
(4)x的整数部分是几 十分位部分是几
请同学们自己算一算,注意组内同学交流哦!
x 0 0.5 1 1.5 2
x2+12x-15 -15 -8.75 -2 5.25 13
下面是小亮的求解过程:
由此,他猜测1<x<1.5.
进一步计算:
x 1.1 1.2 1.3 1.4
x2+12x-15 -0.59 0.84 2.29 3.76
所以1.1<x<1.2,由此他猜测x整数部分是1,十分位部分是1.
你的结果是怎样的呢?
用“两边夹”思想解一元二次方程的步骤:
①在未知数x的取值范围内排除一部分取值;
②根据题意所列的具体情况再次进行排除;
③对列出能反映未知数和方程的值的表格进行再次筛选;
④最终得出未知数的最小取值范围或具体数据.
【规律方法】上述求解是利用了“两边夹”的思想
1.学习了估算ax2+bx+c=0(a,b,c为常数,a≠0)近似解的方法:“两边夹”.
2.知道了估算的步骤:
(1)先确定大致范围.
(2)再取值计算,逐步逼近.
3.想一想:有没有更便捷的方法求一元二次方程的解呢?
1.(天水·中考)若关于x的一元二次方程(m 1)x2+
5x+m2 3m+2=0有一个根是0,则m的值等于( )
A.1 B.2 C.1或2 D.0
B
2.(鞍山 中考)已知x=2是关于x的方程x2-2a=0的一个
解,则2a-1的值为( )
A.6 B.5 C.4 D.3
【解析】选D.把x= 2代入方程x2-2a=0得,4-2a=0,∴a=2.∴2a-1=3.
3.一名跳水运动员进行10m跳台跳水训练,在正常情况下,运动员必须在距水面5m以前完成规定的翻腾动作,并且调整好入水姿势,否则就容易出现失误.假设运动员起跳后的运动时间t(s)和运动员距水面的高度h(m)满足关系:h=10+2.5t-5t2,那么他最多有多长时间完成规定动作
【解析】根据题意,得10+2.5t-5t2=5,即 2t2-t-2=0列表:
t 0 1 2 3
2t2-t-2 -2 -1 4 13
所以1<t<2,进一步列表计算:
所以1.2<t<1.3,因此他完成动作的时间最多不超过1.3s.
t 1.1 1.2 1.3 1.4
2t2-t-2 -0.68 -0.32 0.08 0.52
奋斗就是生活,人生只有前进。
——马克思
第2课时
4.1 一元二次方程
1.回答下列问题:一元二次方程的一般形式是什么?
2.指出下列方程的二次项系数,一次项系数及常数项.
(1)2x2―x+1=0 (2)―x2+1=0
(3)x2―x=0 (4)―x2=0
一般形式:ax2+bx+c=0(a≠0)
答案:
二次项系数
一次项系数
常数项
(1) 2 -1 1
(2) -1 0 1
(3) 1 -1 0
(4) -1 0 0
3.什么叫方程的解,什么叫解方程?
方程的解就是符合方程的未知数的值.
求方程的解的过程叫做解方程.
这节课我们通过估算的方法探索方程的解的大致范围.
1.经历对方程解的探索过程,理解方程解的意义.
2.会估算一元二次方程的解.
1.一块四周镶有宽度相等的花边的地毯如图所示,它的
长为8 m,宽为5 m.如果地毯中央长方形图案的面积为
18m2,则花边多宽
【解析】设花边的宽为x m, 根据题意,可得方程 (8-2x)(5-2x)=18 即:2x2-13x+11=0.
对于方程(8-2x)(5-2x)=18,即2x2-13x+11=0
(1)x可能小于0吗 说说你的理由.
(2)x可能大于4吗 可能大于2.5吗 说说你的理由,并与同伴进行交流.
(3)完成下表:
(4)你知道地毯花边的宽x(m)是多少吗 还有其他求解
方法吗 与同伴进行交流.
x 0 0.5 1 1.5 2 2.5
2x2-13x+11
11
5
0
-4
-7
-9
答案:1m 其他求解方法略
不可能 理由略
不可能 理由略
x
8m
1
10m
7m
6m
【解析】由勾股定理可知,滑动
前梯子底端距墙 m ;
如果设梯子底端滑动x m,那么滑
动后梯子底端距墙 m;
根据题意,可得方程:
72+(x+6)2=102
6
x+6
2.如图,一个长为10m的梯子斜靠在墙上,梯子的顶端距地面的垂直距离为8m.如果梯子的顶端下滑1m,那么梯子的底端滑动多少米?
10m
数学化
在这个问题中,梯子底端滑动的距离x(m)满足方程(x+6)2+72=102,把这个方程化为一般形式为x2+12x-15=0 .
(1)小明认为底端也滑动了1m,他的说法正确吗 为什么
(2)底端滑动的距离可能是2m吗 可能是3m吗 为什么
不正确,因为x=1不满足方程.
不可能,因为x=2,3不满足方程.
(3)你能猜出滑动距离x(m)的大致范围吗
(4)x的整数部分是几 十分位部分是几
请同学们自己算一算,注意组内同学交流哦!
x 0 0.5 1 1.5 2
x2+12x-15 -15 -8.75 -2 5.25 13
下面是小亮的求解过程:
由此,他猜测1<x<1.5.
进一步计算:
x 1.1 1.2 1.3 1.4
x2+12x-15 -0.59 0.84 2.29 3.76
所以1.1<x<1.2,由此他猜测x整数部分是1,十分位部分是1.
你的结果是怎样的呢?
用“两边夹”思想解一元二次方程的步骤:
①在未知数x的取值范围内排除一部分取值;
②根据题意所列的具体情况再次进行排除;
③对列出能反映未知数和方程的值的表格进行再次筛选;
④最终得出未知数的最小取值范围或具体数据.
【规律方法】上述求解是利用了“两边夹”的思想
1.学习了估算ax2+bx+c=0(a,b,c为常数,a≠0)近似解的方法:“两边夹”.
2.知道了估算的步骤:
(1)先确定大致范围.
(2)再取值计算,逐步逼近.
3.想一想:有没有更便捷的方法求一元二次方程的解呢?
1.(天水·中考)若关于x的一元二次方程(m 1)x2+
5x+m2 3m+2=0有一个根是0,则m的值等于( )
A.1 B.2 C.1或2 D.0
B
2.(鞍山 中考)已知x=2是关于x的方程x2-2a=0的一个
解,则2a-1的值为( )
A.6 B.5 C.4 D.3
【解析】选D.把x= 2代入方程x2-2a=0得,4-2a=0,∴a=2.∴2a-1=3.
3.一名跳水运动员进行10m跳台跳水训练,在正常情况下,运动员必须在距水面5m以前完成规定的翻腾动作,并且调整好入水姿势,否则就容易出现失误.假设运动员起跳后的运动时间t(s)和运动员距水面的高度h(m)满足关系:h=10+2.5t-5t2,那么他最多有多长时间完成规定动作
【解析】根据题意,得10+2.5t-5t2=5,即 2t2-t-2=0列表:
t 0 1 2 3
2t2-t-2 -2 -1 4 13
所以1<t<2,进一步列表计算:
所以1.2<t<1.3,因此他完成动作的时间最多不超过1.3s.
t 1.1 1.2 1.3 1.4
2t2-t-2 -0.68 -0.32 0.08 0.52
奋斗就是生活,人生只有前进。
——马克思
同课章节目录
- 第1章 图形的相似
- 1.1 相似多边形
- 1.2 怎样判定三角形相似
- 1.3 相似三角形的性质
- 1.4 图形的位似
- 第2章 解直角三角形
- 2.1 锐角三角比
- 2.2 30°,45°,60°角的三角比
- 2.3 用计算器求锐角三角比
- 2.4 解直角三角形
- 2.5 解直角三角形的应用
- 第3章 对圆的进一步认识
- 3.1 圆的对称性
- 3.2 确定圆的条件
- 3.3 圆周角
- 3.4 直线与圆的位置关系
- 3.5 三角形的内切圆
- 3.6 弧长及扇形面积的计算
- 3.7 正多边形与圆
- 课题学习 图形变换与图案设计
- 第4章 一元二次方程
- 4.1 一元二次方程
- 4.2 用配方法解一元二次方程
- 4.3 用公式法解一元二次方程
- 4.4 用因式分解法解一元二次方程
- 4.5 一元二次方程的应用
- 4.6 一元二次方程根与系数的关系
