人教版数学八年级上册13.3.1等腰三角形 精品同步练习(含解析)
文档属性
| 名称 | 人教版数学八年级上册13.3.1等腰三角形 精品同步练习(含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-17 14:31:02 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
人教版八年级上册数学 13.3.1等腰三角形 同步练习
(考试时间:60分钟 满分:100分)
选择题(本大题共10小题,每小题3分,共30分。下列各题的备选答案中,只有一项是最符合题意的,请选出。)
1.如图,△ABC中,AB=AC,∠B=70°,则∠A的度数是
A.70° B.55° C.50° D.40°
2.如图所示,在锐角△ABC中,点D、E分别是边AC、BC的中点,且DA=DE,那么下列结论错误的是
A.∠1=∠2 B.∠1=∠3 C.∠B=∠C D.∠3=∠B
3.如图,在△ABC中,AB=AC,AD⊥BC于点D,若AB=6,CD=4,则△ABC的周长是
A.21 B.20 C.19 D.18
4.一个等腰三角形的顶角是底角的4倍,则其顶角的度数为
A.20° B.30° C.80° D.120°
5.等腰三角形的周长为13 cm,其中一边长为3 cm,则该等腰三角形的底边为
A.7 cm B.3 cm
C.7 cm或3 cm D.8 cm
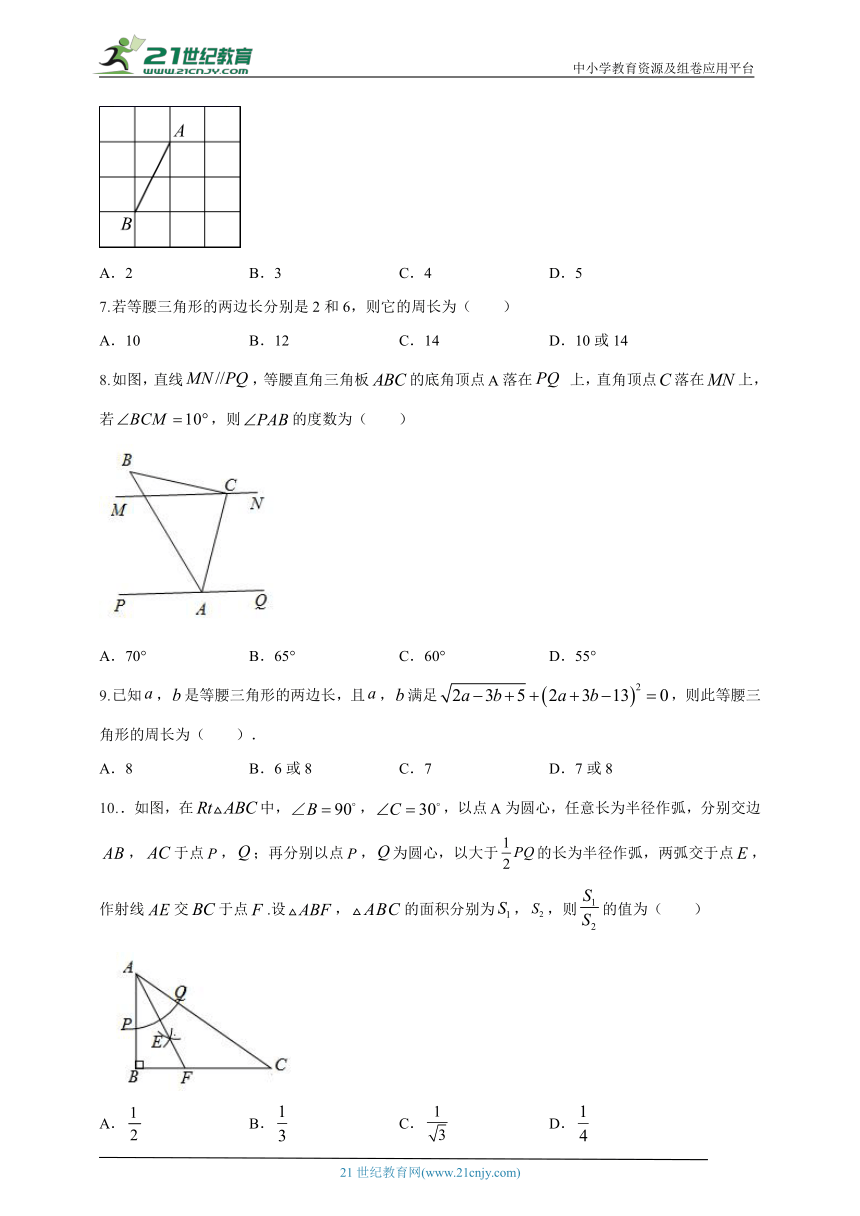
6.如图,在的正方形网格中有两个格点A、B,连接,在网格中再找一个格点C,使得是等腰直角三角形,满足条件的格点C的个数是( )
A.2 B.3 C.4 D.5
7.若等腰三角形的两边长分别是2和6,则它的周长为( )
A.10 B.12 C.14 D.10或14
8.如图,直线,等腰直角三角板的底角顶点落在 上,直角顶点落在上,若,则的度数为( )
A.70° B.65° C.60° D.55°
9.已知,是等腰三角形的两边长,且,满足,则此等腰三角形的周长为( ).
A.8 B.6或8 C.7 D.7或8
10..如图,在中,,,以点为圆心,任意长为半径作弧,分别交边,于点,;再分别以点,为圆心,以大于的长为半径作弧,两弧交于点,作射线交于点.设,的面积分别为,,则的值为( )
A. B. C. D.
二、填空题(本大题共5小题,每小题4分,共20分。)
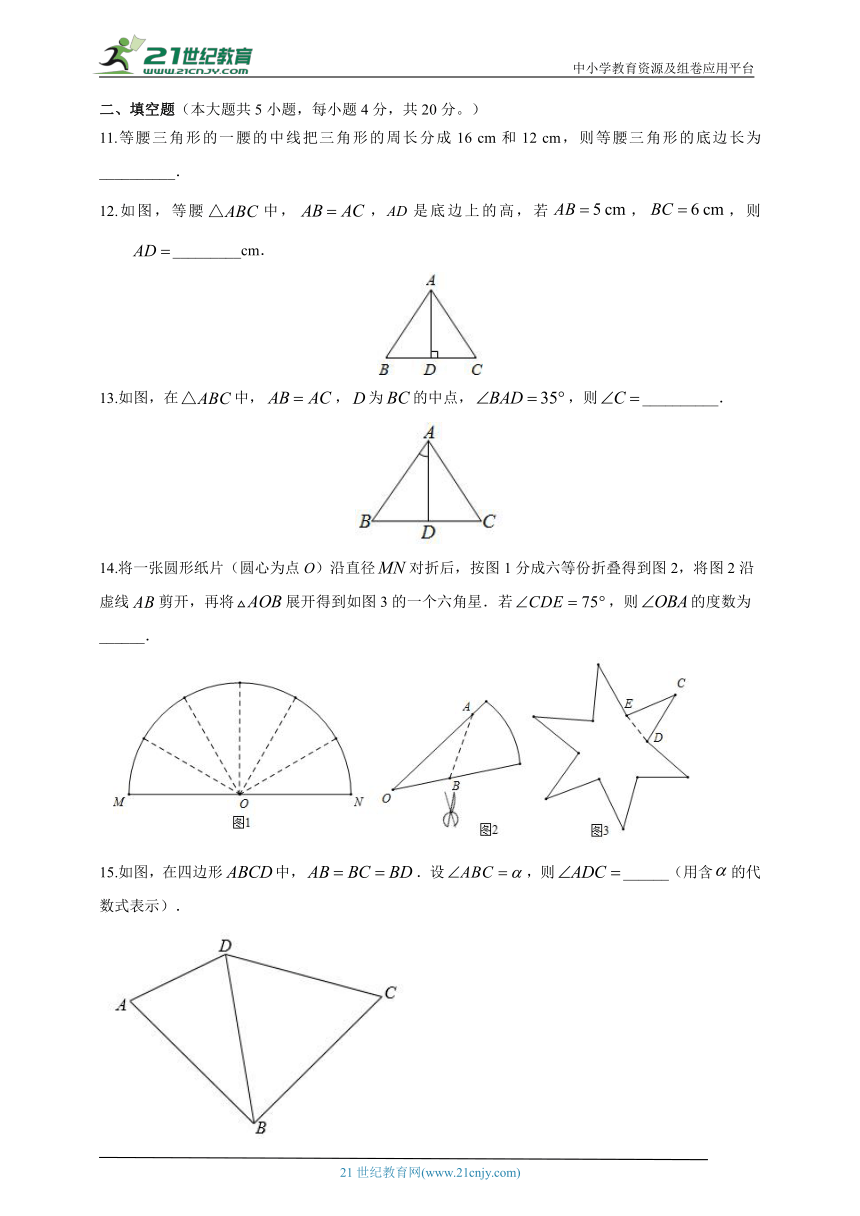
11.等腰三角形的一腰的中线把三角形的周长分成16 cm和12 cm,则等腰三角形的底边长为__________.
12.如图,等腰中,,AD是底边上的高,若,,则_________cm.
13.如图,在中,,为的中点,,则__________.
14.将一张圆形纸片(圆心为点O)沿直径对折后,按图1分成六等份折叠得到图2,将图2沿虚线剪开,再将展开得到如图3的一个六角星.若,则的度数为______.
15.如图,在四边形中,.设,则______(用含的代数式表示).
三、解答题(本大题共5小题,每小题10分,共50分。解答应写出文字说明、证明过程或演算步骤.)
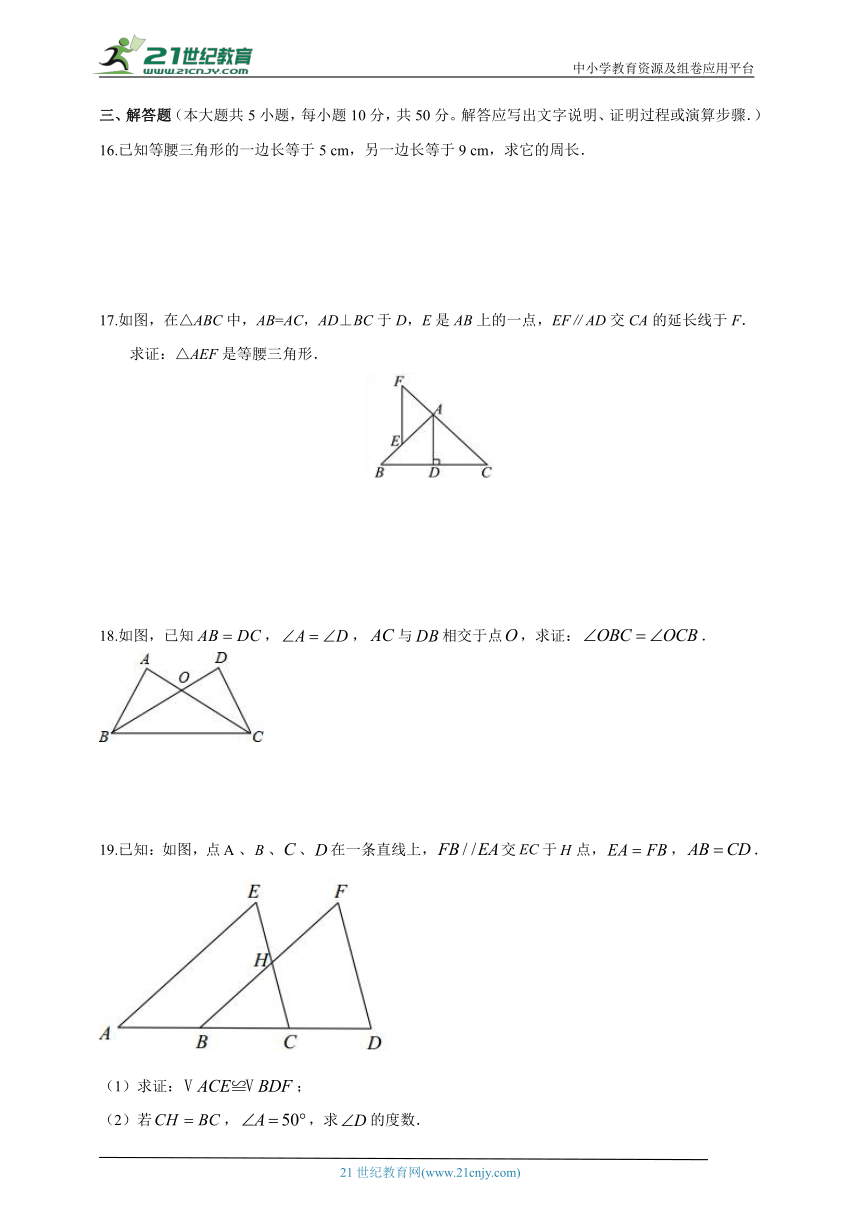
16.已知等腰三角形的一边长等于5 cm,另一边长等于9 cm,求它的周长.
17.如图,在△ABC中,AB=AC,AD⊥BC于D,E是AB上的一点,EF∥AD交CA的延长线于F.
求证:△AEF是等腰三角形.
18.如图,已知,,与相交于点,求证:.
19.已知:如图,点、、、在一条直线上,交于点,,.
(1)求证:;
(2)若,,求的度数.
20.如图,,.求证:.
参考答案
选择题
1.【答案】D
【解析】∵AB=AC,∴∠B=∠C,∵∠B=70°,∴∠C=70°,∵∠A+∠B+∠C=180°,∴∠A=40°.故选D.
2.【答案】D
【解析】∵点D、E分别是边AC、BC的中点,且DA=DE,∴DA=DC=DE.
∴∠2=∠3,AE⊥BC,DE∥AB,∴∠1=∠2,∠B=∠C.故选D.
3.【答案】B
【解析】∵在△ABC中,AB=AC,∴△ABC是等腰三角形,又∵AD⊥BC于点D,∴BD=CD.∵AB=6,CD=4,∴△ABC的周长=6+4+4+6=20.故选B.
4.【答案】D
【解析】设底角为x,顶角为4x.则2x+4x=180°,解得x=30°,∴4x=120°,故选D.
5.【答案】B
【解析】当腰是3 cm时,则另两边是3 cm,7 cm.而3+3<7,不满足三边关系定理,因而应舍去.
底边是3 cm时,另两边长是5 cm,5 cm.则该等腰三角形的底边为3 cm.故选B.
6.【答案】B
【分析】根据题意,结合图形,分两种情况讨论:①AB为等腰直角△ABC底边;②AB为等腰直角△ABC其中的一条腰.
【详解】如图:分情况讨论:
①AB为等腰直角△ABC底边时,符合条件的C点有0个;
②AB为等腰直角△ABC其中的一条腰时,符合条件的C点有3个.
故共有3个点,
故选:B.
7.【答案】C
【分析】分腰为2和6两种情况分别讨论,再根据三角形的三边关系进行取舍,再求周长即可.
【详解】当腰为2时,则三边为2、2、6,此时2+2<6,不满足三角形的三边关系,不符合题意;
当腰为6时,则三边为6、6、2,满足三角形的三边关系,周长为14;
故选:C.
8.【答案】D
【分析】根据条件可得∠MCA=80゜,由,可得∠CAQ=∠MCA,根据等腰直角三角形的性质则可求得结果.
【详解】∵由题意知,∠ACB=90゜,∠BAC=45゜
∴∠MCA=∠ACB-∠BCM==90゜-10゜=80゜
∵
∴∠CAQ=∠MCA=80゜
∴∠PAB=180゜-∠BAC-∠CAQ=55゜
故选:D.
9.【答案】D
【分析】先根据非负数的性质列式求出a、b的值,再分a的值是腰长与底边两种情况讨论求解.
【详解】∵,
∴
解得,
①2是腰长时,三角形的三边分别为2、2、3,能组成三角形,周长=2+2+3=7;
②2是底边时,三角形的三边分别为2、3、3,能组成三角形,周长=2+3+3=8,
所以该等腰三角形的周长为7或8.
故选:D.
10.【答案】B
【分析】根据作图过程可得是的平分线,根据角平分线的性质和,,可得,设,则,,根据三角形的面积公式分别求出,,再计算即可.
【详解】根据作图过程可知:是的平分线,
∴,
∵,,
∴
∴,
∴
∴
设,则在中,
∴,,
∴,,
∴,
故选:B.
填空题
11.【答案】cm或12 cm
【解析】设等腰三角形的腰长是x,底边是y,
根据题意得或,解得或,
经检验,均符合三角形的三边关系.因此三角形的底边是或12.故答案为:cm或12 cm.
12.【答案】4
【解析】根据等腰三角形的三线合一可得:BD=BC=×6=3 cm,
在直角△ABD中,由勾股定理得:AB2=BD2+AD2,
所以,AD=4 cm.故答案为:4.
13.【答案】55°
【解析】,为的中点,,所以∠BAC=70°,∠C==55°.故答案为:55°.
14.【答案】135°
【分析】利用折叠的性质,根据等腰三角形的性质及三角形内角和定理解题.
【详解】连接OC,EO
由折叠性质可得:∠EOC=,EC=DC,OC平分∠ECD
∴∠ECO=
∴∠OEC=180°-∠ECO-∠EOC=135°
即的度数为135°
故答案为:135°
15.【答案】
【分析】由等腰的性质可得:∠ADB=,∠BDC=,两角相加即可得到结论.
【详解】在△ABD中,AB=BD
∴∠A=∠ADB=
在△BCD中,BC=BD
∴∠C=∠BDC=
∵
∴
=
=
=
=
故答案为:.
解答题
16.【解析】5是腰长时,则周长是5+5+9=19 cm;
5是底边时,则5+9+9=23 cm.
所以周长为19 cm或23 cm.
17.【解析】∵AB=AC,AD⊥BC,∴∠BAD=∠CAD.
又∵AD∥EF,∴∠F=∠CAD,∠FEA=∠BAD,
∴∠FEA=∠F,∴△AEF是等腰三角形.
18.【答案】证明见解析
【分析】根据全等三角形的性质,通过证明,得,结合等腰三角形的性质,即可得到答案.
【详解】∵,
∴(AAS),
∴,
∴.
19.【答案】(1)见解析;(2)80°
【分析】(1)由,利用同位角相等可得.由,利用等式性质可得,可证;
(2)由可得,由利用等角对等边,可求.利用三角形内角和可得.利用性质,可得.
【详解】(1)证明:∵,
∴.
∵,
∴,即,
在和中,
∵,
∴.
(2)解:,
∴,
∵,
∴.
∴.
∵,
∴.
20.【答案】见解析.
【分析】利用SAS可证明△ABD≌△BAC,即可得∠ABD=∠BAC,进而可证明结论.
【详解】证明:在和中,
∵
∴≌(SAS)
∴,∴.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
人教版八年级上册数学 13.3.1等腰三角形 同步练习
(考试时间:60分钟 满分:100分)
选择题(本大题共10小题,每小题3分,共30分。下列各题的备选答案中,只有一项是最符合题意的,请选出。)
1.如图,△ABC中,AB=AC,∠B=70°,则∠A的度数是
A.70° B.55° C.50° D.40°
2.如图所示,在锐角△ABC中,点D、E分别是边AC、BC的中点,且DA=DE,那么下列结论错误的是
A.∠1=∠2 B.∠1=∠3 C.∠B=∠C D.∠3=∠B
3.如图,在△ABC中,AB=AC,AD⊥BC于点D,若AB=6,CD=4,则△ABC的周长是
A.21 B.20 C.19 D.18
4.一个等腰三角形的顶角是底角的4倍,则其顶角的度数为
A.20° B.30° C.80° D.120°
5.等腰三角形的周长为13 cm,其中一边长为3 cm,则该等腰三角形的底边为
A.7 cm B.3 cm
C.7 cm或3 cm D.8 cm
6.如图,在的正方形网格中有两个格点A、B,连接,在网格中再找一个格点C,使得是等腰直角三角形,满足条件的格点C的个数是( )
A.2 B.3 C.4 D.5
7.若等腰三角形的两边长分别是2和6,则它的周长为( )
A.10 B.12 C.14 D.10或14
8.如图,直线,等腰直角三角板的底角顶点落在 上,直角顶点落在上,若,则的度数为( )
A.70° B.65° C.60° D.55°
9.已知,是等腰三角形的两边长,且,满足,则此等腰三角形的周长为( ).
A.8 B.6或8 C.7 D.7或8
10..如图,在中,,,以点为圆心,任意长为半径作弧,分别交边,于点,;再分别以点,为圆心,以大于的长为半径作弧,两弧交于点,作射线交于点.设,的面积分别为,,则的值为( )
A. B. C. D.
二、填空题(本大题共5小题,每小题4分,共20分。)
11.等腰三角形的一腰的中线把三角形的周长分成16 cm和12 cm,则等腰三角形的底边长为__________.
12.如图,等腰中,,AD是底边上的高,若,,则_________cm.
13.如图,在中,,为的中点,,则__________.
14.将一张圆形纸片(圆心为点O)沿直径对折后,按图1分成六等份折叠得到图2,将图2沿虚线剪开,再将展开得到如图3的一个六角星.若,则的度数为______.
15.如图,在四边形中,.设,则______(用含的代数式表示).
三、解答题(本大题共5小题,每小题10分,共50分。解答应写出文字说明、证明过程或演算步骤.)
16.已知等腰三角形的一边长等于5 cm,另一边长等于9 cm,求它的周长.
17.如图,在△ABC中,AB=AC,AD⊥BC于D,E是AB上的一点,EF∥AD交CA的延长线于F.
求证:△AEF是等腰三角形.
18.如图,已知,,与相交于点,求证:.
19.已知:如图,点、、、在一条直线上,交于点,,.
(1)求证:;
(2)若,,求的度数.
20.如图,,.求证:.
参考答案
选择题
1.【答案】D
【解析】∵AB=AC,∴∠B=∠C,∵∠B=70°,∴∠C=70°,∵∠A+∠B+∠C=180°,∴∠A=40°.故选D.
2.【答案】D
【解析】∵点D、E分别是边AC、BC的中点,且DA=DE,∴DA=DC=DE.
∴∠2=∠3,AE⊥BC,DE∥AB,∴∠1=∠2,∠B=∠C.故选D.
3.【答案】B
【解析】∵在△ABC中,AB=AC,∴△ABC是等腰三角形,又∵AD⊥BC于点D,∴BD=CD.∵AB=6,CD=4,∴△ABC的周长=6+4+4+6=20.故选B.
4.【答案】D
【解析】设底角为x,顶角为4x.则2x+4x=180°,解得x=30°,∴4x=120°,故选D.
5.【答案】B
【解析】当腰是3 cm时,则另两边是3 cm,7 cm.而3+3<7,不满足三边关系定理,因而应舍去.
底边是3 cm时,另两边长是5 cm,5 cm.则该等腰三角形的底边为3 cm.故选B.
6.【答案】B
【分析】根据题意,结合图形,分两种情况讨论:①AB为等腰直角△ABC底边;②AB为等腰直角△ABC其中的一条腰.
【详解】如图:分情况讨论:
①AB为等腰直角△ABC底边时,符合条件的C点有0个;
②AB为等腰直角△ABC其中的一条腰时,符合条件的C点有3个.
故共有3个点,
故选:B.
7.【答案】C
【分析】分腰为2和6两种情况分别讨论,再根据三角形的三边关系进行取舍,再求周长即可.
【详解】当腰为2时,则三边为2、2、6,此时2+2<6,不满足三角形的三边关系,不符合题意;
当腰为6时,则三边为6、6、2,满足三角形的三边关系,周长为14;
故选:C.
8.【答案】D
【分析】根据条件可得∠MCA=80゜,由,可得∠CAQ=∠MCA,根据等腰直角三角形的性质则可求得结果.
【详解】∵由题意知,∠ACB=90゜,∠BAC=45゜
∴∠MCA=∠ACB-∠BCM==90゜-10゜=80゜
∵
∴∠CAQ=∠MCA=80゜
∴∠PAB=180゜-∠BAC-∠CAQ=55゜
故选:D.
9.【答案】D
【分析】先根据非负数的性质列式求出a、b的值,再分a的值是腰长与底边两种情况讨论求解.
【详解】∵,
∴
解得,
①2是腰长时,三角形的三边分别为2、2、3,能组成三角形,周长=2+2+3=7;
②2是底边时,三角形的三边分别为2、3、3,能组成三角形,周长=2+3+3=8,
所以该等腰三角形的周长为7或8.
故选:D.
10.【答案】B
【分析】根据作图过程可得是的平分线,根据角平分线的性质和,,可得,设,则,,根据三角形的面积公式分别求出,,再计算即可.
【详解】根据作图过程可知:是的平分线,
∴,
∵,,
∴
∴,
∴
∴
设,则在中,
∴,,
∴,,
∴,
故选:B.
填空题
11.【答案】cm或12 cm
【解析】设等腰三角形的腰长是x,底边是y,
根据题意得或,解得或,
经检验,均符合三角形的三边关系.因此三角形的底边是或12.故答案为:cm或12 cm.
12.【答案】4
【解析】根据等腰三角形的三线合一可得:BD=BC=×6=3 cm,
在直角△ABD中,由勾股定理得:AB2=BD2+AD2,
所以,AD=4 cm.故答案为:4.
13.【答案】55°
【解析】,为的中点,,所以∠BAC=70°,∠C==55°.故答案为:55°.
14.【答案】135°
【分析】利用折叠的性质,根据等腰三角形的性质及三角形内角和定理解题.
【详解】连接OC,EO
由折叠性质可得:∠EOC=,EC=DC,OC平分∠ECD
∴∠ECO=
∴∠OEC=180°-∠ECO-∠EOC=135°
即的度数为135°
故答案为:135°
15.【答案】
【分析】由等腰的性质可得:∠ADB=,∠BDC=,两角相加即可得到结论.
【详解】在△ABD中,AB=BD
∴∠A=∠ADB=
在△BCD中,BC=BD
∴∠C=∠BDC=
∵
∴
=
=
=
=
故答案为:.
解答题
16.【解析】5是腰长时,则周长是5+5+9=19 cm;
5是底边时,则5+9+9=23 cm.
所以周长为19 cm或23 cm.
17.【解析】∵AB=AC,AD⊥BC,∴∠BAD=∠CAD.
又∵AD∥EF,∴∠F=∠CAD,∠FEA=∠BAD,
∴∠FEA=∠F,∴△AEF是等腰三角形.
18.【答案】证明见解析
【分析】根据全等三角形的性质,通过证明,得,结合等腰三角形的性质,即可得到答案.
【详解】∵,
∴(AAS),
∴,
∴.
19.【答案】(1)见解析;(2)80°
【分析】(1)由,利用同位角相等可得.由,利用等式性质可得,可证;
(2)由可得,由利用等角对等边,可求.利用三角形内角和可得.利用性质,可得.
【详解】(1)证明:∵,
∴.
∵,
∴,即,
在和中,
∵,
∴.
(2)解:,
∴,
∵,
∴.
∴.
∵,
∴.
20.【答案】见解析.
【分析】利用SAS可证明△ABD≌△BAC,即可得∠ABD=∠BAC,进而可证明结论.
【详解】证明:在和中,
∵
∴≌(SAS)
∴,∴.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
