人教版数学八年级上册13.4最短路径问题 精品同步练习(含解析)
文档属性
| 名称 | 人教版数学八年级上册13.4最短路径问题 精品同步练习(含解析) | 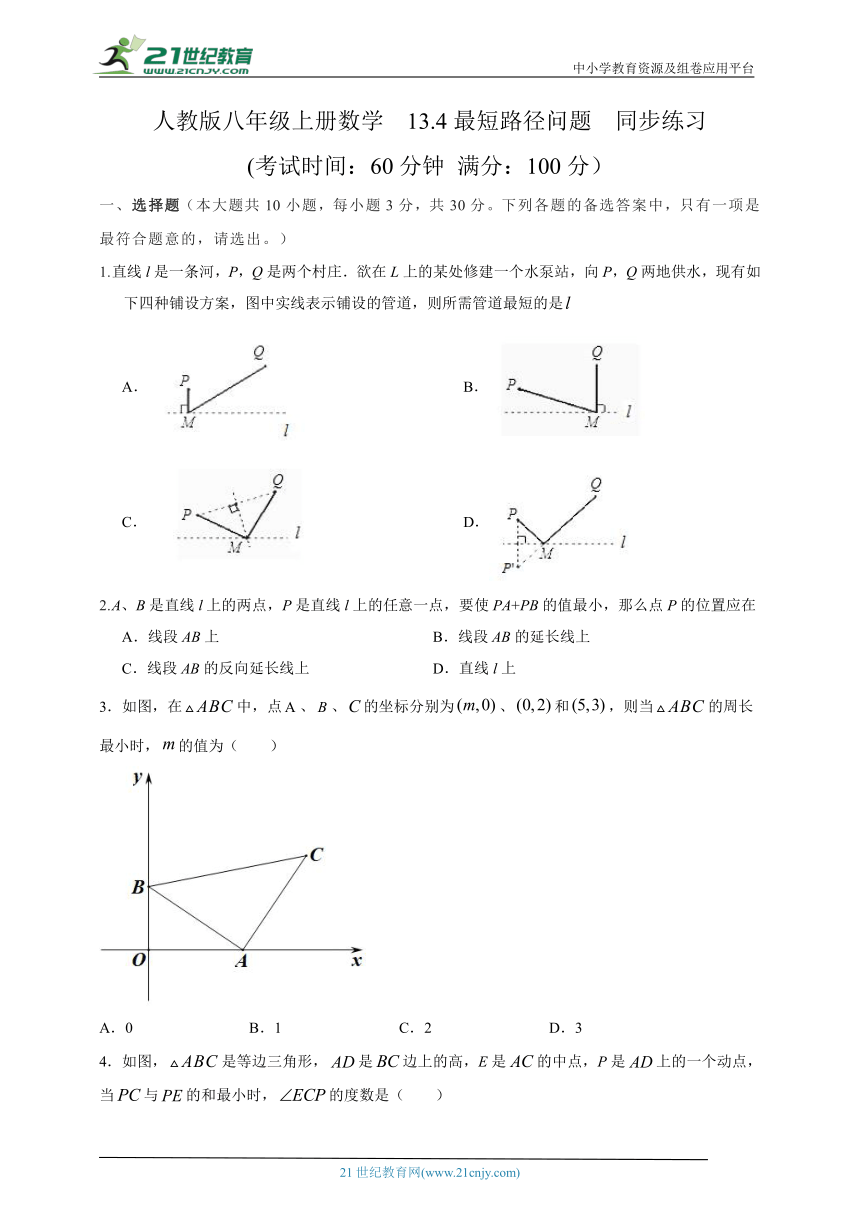 | |
| 格式 | doc | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-17 15:03:29 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
人教版八年级上册数学 13.4最短路径问题 同步练习
(考试时间:60分钟 满分:100分)
选择题(本大题共10小题,每小题3分,共30分。下列各题的备选答案中,只有一项是最符合题意的,请选出。)
1.直线l是一条河,P,Q是两个村庄.欲在L上的某处修建一个水泵站,向P,Q两地供水,现有如下四种铺设方案,图中实线表示铺设的管道,则所需管道最短的是
A. B.
C. D.
2.A、B是直线l上的两点,P是直线l上的任意一点,要使PA+PB的值最小,那么点P的位置应在
A.线段AB上 B.线段AB的延长线上
C.线段AB的反向延长线上 D.直线l上
3.如图,在中,点、、的坐标分别为、和,则当的周长最小时,的值为( )
A.0 B.1 C.2 D.3
4.如图,是等边三角形,是边上的高,E是的中点,P是上的一个动点,当与的和最小时,的度数是( )
A. B. C. D.
5.如图,△ABC是等边三角形,AD是BC边上的高,E是AC的中点,P是AD上的一个动点,当PC与PE的和最小时,∠ACP的度数是( )
A.30° B.45° C.60° D.90°
6.在中,,,于点,且,若点在边上移动,则的最小值是( )
A.4.5 B.4.6 C.4.7 D.4.8
7.如图,在锐角△ABC中,AB=AC=10,S△ABC =25,∠BAC的平分线交BC于点D,点M,N分别是AD和AB上的动点,则BM+MN的最小值是( )
A.4 B. C.5 D.6
8.已知点A,B是两个居民区的位置,现在准备在墙l边上建立一个垃圾站点P,如图是4位设计师给出的规划图,其中PA+PB距离最短的是()
A. B.
C. D.
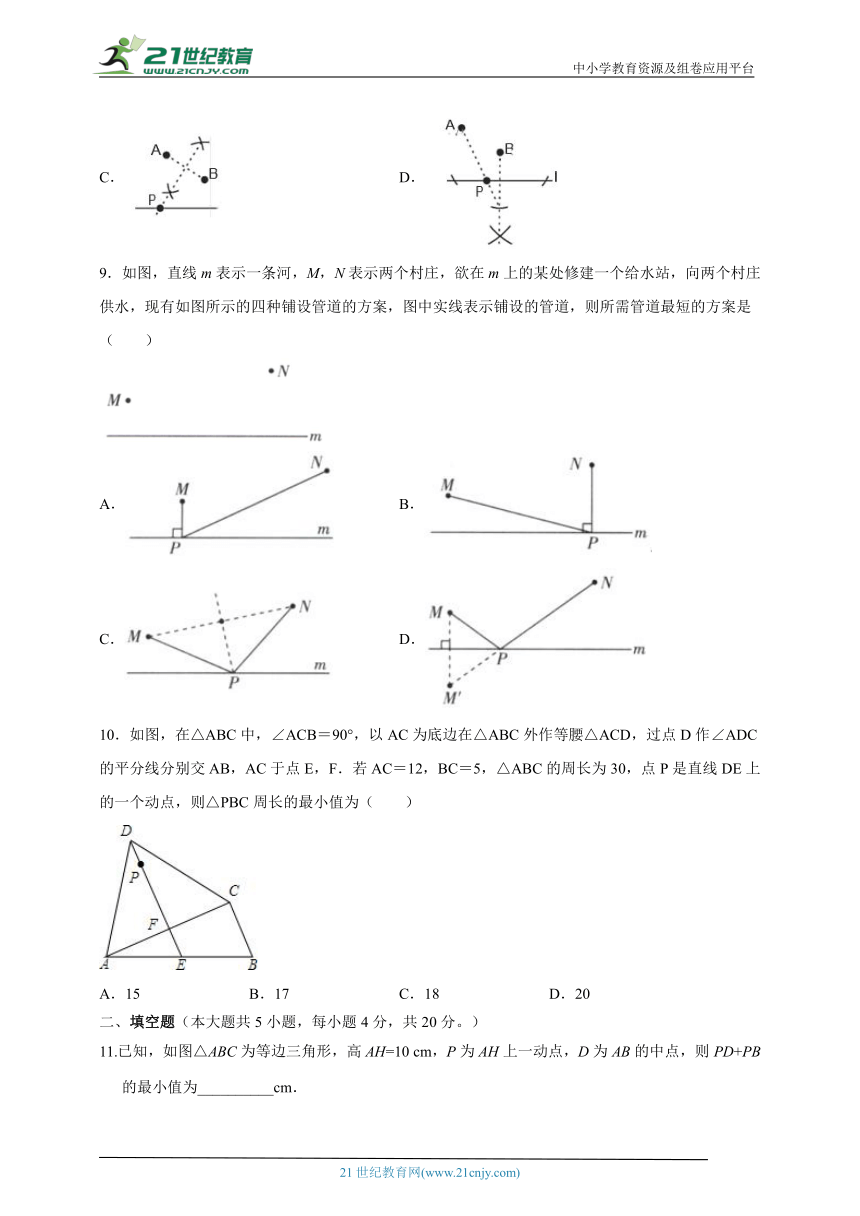
9.如图,直线m表示一条河,M,N表示两个村庄,欲在m上的某处修建一个给水站,向两个村庄供水,现有如图所示的四种铺设管道的方案,图中实线表示铺设的管道,则所需管道最短的方案是( )
A. B.
C. D.
10.如图,在△ABC中,∠ACB=90°,以AC为底边在△ABC外作等腰△ACD,过点D作∠ADC的平分线分别交AB,AC于点E,F.若AC=12,BC=5,△ABC的周长为30,点P是直线DE上的一个动点,则△PBC周长的最小值为( )
A.15 B.17 C.18 D.20
填空题(本大题共5小题,每小题4分,共20分。)
11.已知,如图△ABC为等边三角形,高AH=10 cm,P为AH上一动点,D为AB的中点,则PD+PB的最小值为__________cm.
12.如图,在锐角中,,边上有一定点分别是和边上的动点,当的周长最小时,的度数是_________.
13.如图,在平面直角坐标系xOy中,点A的坐标为(0,6),点B为x轴上一动点,以AB为边在直线AB的右侧作等边三角形ABC.若点P为OA的中点,连接PC,则PC的长的最小值为_____.
14.如图,等边△ABC的边长为4,点D在边AC上,AD=1.
(1)△ABC的周长等于_____;
(2)线段PQ在边BA上运动,PQ=1,BQ>BP,连接QD,PC,当四边形PCDQ的周长取得最小值时,请在如图所示的矩形区域内,用无刻度的直尺和圆规,画出线段PC,QD,并简要说明点P和点Q的位置是如何找到的(保留作图痕迹,不要求证明)_____.
15.如图,等腰△ABC底边BC的长为6cm,面积是24cm2,腰AB的垂直平分线MN交AB于点M,交AC于点N,若D为BC边上的中点,E为线段MN上一动点,则△BDE的周长最小值为____cm.
三、解答题(本大题共5小题,每小题10分,共50分。解答应写出文字说明、证明过程或演算步骤.)
16.要在燃气管道L上修建一个泵站P,分别向A,B两镇供气,泵站修在管道的什么地方,可使所用的输气管线最短?在图上画出P点位置,不写作法,保留痕迹.
17.如图,小明在A处放牛,要到河边(直线l)给牛喝水,喝完水把牛赶回家中B处.
(1)要使路程最短,应该在河边哪处给牛喝水,请在直线l上画出喝水处点P的位置;
(2)在直线l上任取一点Q(点Q不与点P重合),连接,试说明.
18.如图,BA、BC是两条公路,在两条公路夹角内部的点P处有一油库,若在两公路上分别建个加油站,并使运油的油罐车从油库出发先到一加油站,再到另一加油站,最后回到油库的路程最短,则加油站应如何选址?
19.如图,平面直角坐标系中,△ABC的顶点坐标分别为A(4,1),B(3,4),C(1,2).
(1)画出△ABC关于y轴对称的△A1B1C1,并写出顶点C1的坐标;
(2)若点P在x轴上,且满足PA+PC1最小,求点P的坐标及PA+PC1的最小值.
20.如图,在等腰三角形ABC中,底边,的面积是,腰AB的垂直平分线EF分别交AB、AC于点E、F,点D为BC边上的中点,M为EF上的动点.
(1)当周长的最小时,请在图中作出满足条件的(保留作图痕迹,不要求写出画法).
(2)周长的最小值是___________.
参考答案
选择题
1.【答案】D
【解析】本题的依据就是两点之间线段最短.首先作点P关于直线l的对称点P′,连接P′Q就是最短的路程.故选D.
2.【答案】A
3.【答案】C
【分析】做出B关于x轴对称点为B′,连接B′C,交x轴于点A',此时的周长最小,由等腰直角三角形的性质可求∠OB'A'=∠OA'B'=45°,可求OB'=OA'=1,即可求解.
【详解】如图所示,做出B关于x轴对称点为B′,连接B′C,交x轴于点A',此时△ABC周长最小
过点C作CH⊥x轴,过点B'作B'H⊥y轴,交CH于H,
∵B(0,2),
∴B′(0,-2),
∵C(5,3),
∴CH= B′H=5,
∴∠CB'H=45°,
∴∠BB' A'=45°,
∴∠OB'A'=∠OA'B'=45°,
∴OB'=OA'=2,
则此时A'坐标为(2,0).
m的值为2.
故选:C.
4.【答案】A
【分析】连接BE,则BE的长度即为PE与PC和的最小值.再利用等边三角形的性质可得∠PBC=∠PCB=30°,即可解决问题;
【详解】如连接BE,与AD交于点P,此时PE+PC最小,
∵△ABC是等边三角形,AD⊥BC,
∴PC=PB,
∴PE+PC=PB+PE=BE,
即BE就是PE+PC的最小值,
∵△ABC是等边三角形,
∴∠BCE=60°,
∵BA=BC,AE=EC,
∴BE⊥AC,
∴∠BEC=90°,
∴∠EBC=30°,
∵PB=PC,
∴∠PCB=∠PBC=30°,
∴∠ECP=∠ACB-∠PCB=30°,
故选:A.
5.【答案】A
【分析】连接BE,则BE的长度即为PE与PC和的最小值.再利用等边三角形的性质可得∠PBC=∠PCB=30°,即可解决问题;
【详解】如图,连接BE,与AD交于点P,此时PE+PC最小,
∵△ABC是等边三角形,AD⊥BC,
∴PC=PB,
∴PE+PC=PB+PE=BE,
即BE就是PE+PC的最小值,
∵△ABC是等边三角形,
∴∠BCE=60°,
∵BA=BC,AE=EC,
∴BE⊥AC,
∴∠BEC=90°,
∴∠EBC=30°,
∵PB=PC,
∴∠PCB=∠PBC=30°,
∴∠ACP =30°,
故选:A.
6.【答案】D
【分析】根据最短路径问题得:当BP⊥AC时,的值最小,利用面积关系得到,代入数值求出答案.
【详解】由题意得:当BP⊥AC时,的值最小,
∵,
∴,
解得BP=,
故选:D.
7.【答案】C
【分析】根据AD是∠BAC的平分线,AB=AC可得出确定出点B关于AD的对称点为点C,根据垂线段最短,过点C作CN⊥AB于N交AD于M,根据轴对称确定最短路线问题,点M即为使BM+MN最小的点,CN=BM+MN,利用三角形的面积求出CN,从而得解.
【详解】如图,∵AD是∠BAC的平分线,AB=AC,
∴点B关于AD的对称点为点C,
过点C作CN⊥AB于N交AD于M,
由轴对称确定最短路线问题,点M即为使BM+MN最小的点,CN=BM+MN,
∵AB=10,S△ABC=25,
∴×10 CN=25,
解得CN=5,
即BM+MN的最小值是5.
故选:C.
8.【答案】D
【分析】根据轴对称的性质以及线段的性质可得到结论.
【详解】根据题意知,在墙l边上建立一个垃圾站点P,使PA+PB距离最小,则作A或者B关于l的对称点,然后连接找到点P,则D选项符合要求.
故选:D
9.【答案】D
【分析】本题可通过找点M或点N关于直线m的对称点,继而利用两点之间线段最短确定最短路径.
【详解】作点M关于直线m的对称点,连接交直线m于P,则P处即为给水站位置.根据“两点之间,线段最短”可排除、、选项,可知选项管道最短.
故选:.
10.【答案】C
【分析】根据点与点关于对称,即可得出,当点与点重合时,,此时的周长最小,根据与的长即可得到周长的最小值.
【详解】是以为底边的等腰三角形,平分,
垂直平分,
点与点关于对称,
,
如图所示,当点与点重合时,,
此时的周长最小,
,,的周长为30,
,
周长的最小值为,
故选:.
填空题
11.【答案】10
【解析】如图,连接PC,
∵△ABC为等边三角形,D为AB的中点,
∴CD⊥AB,
∴CD=AH=10 cm.
∵AH⊥BC,∴PB=PC,
∴PD+PB的最小值为:PD+PB=PC+PD=CD=AH=10 cm.
故答案为:10.
12.【答案】80°
【分析】根据对称的性质,易求得∠C+∠EPF=180°,由 ∠ACB=50°,易求得∠D+∠G=50°,继而求得答案;
【详解】∵ PD⊥AC,PG⊥BC,
∴∠PEC=∠PFC=90°,
∴ ∠C+∠EPF=180°,
∵∠C=50°,
∵∠D+∠G+∠EPF=180°,
∴ ∠D+∠G=50°,
由对称可知:∠G=∠GPN,∠D=∠DPM, L
∴∠GPN+∠DPM=50°,
∴∠MPN=130°-50°=80°,
故答案为:80°.
13.【答案】
【分析】以AP为边作等边三角形APE,连接BE,过点E作EF⊥AP于F,由“SAS”可证△ABE≌△ACP,可得BE=PC,则当BE有最小值时,PC有最小值,即可求解.
【详解】如图,以AP为边作等边三角形APE,连接BE,过点E作EF⊥AP于F,
∵点A的坐标为(0,6),
∴OA=6,
∵点P为OA的中点,
∴AP=3,
∵△AEP是等边三角形,EF⊥AP,
∴AF=PF=,AE=AP,∠EAP=∠BAC=60°,
∴∠BAE=∠CAP,
在△ABE和△ACP中,
∴△ABE≌△ACP(SAS),
∴BE=PC,
∴当BE有最小值时,PC有最小值,
即BE⊥x轴时,BE有最小值,
∴BE的最小值为OF=OP+PF=3+=,
∴PC的最小值为,
故答案为.
14.【答案】12 见解析,过点C作CE∥AB,且CE=1,作点D关于AB的对称点F,连接EF交AB于一点为Q,在AB上BQ之间截取PQ=1,连接CP、DQ,则四边形PCDQ为所求的周长最小的四边形
【分析】(1)根据三角形周长公式计算;
(2)过点C作CE∥AB,且CE=1,作点D关于AB的对称点F,连接EF交AB于一点为Q,在AB上BQ之间截取PQ=1,连接CP、DQ,则四边形PCDQ为所求的周长最小的四边形.
【详解】(1)△ABC的周长等于,
故答案为:12;
(2)如图:
故答案为:过点C作CE∥AB,且CE=1,作点D关于AB的对称点F,连接EF交AB于一点为Q,在AB上BQ之间截取PQ=1,连接CP、DQ,则四边形PCDQ为所求的周长最小的四边形.
.
15.【答案】11
【分析】连接AD,由于△ABC是等腰三角形,点D是BC边的中点,故AD⊥BC,再根据三角形的面积公式求出AD的长,再根据MN是线段AB的垂直平分线可知,点B关于直线NM的对称点为点A,故AD的长为BE+ED的最小值,由此即可得出结论.
【详解】连接AD,
∵△ABC是等腰三角形,点D是BC边的中点,
∴AD⊥BC,BD=3cm
解得AD=8(cm),
∵MN是线段AB的垂直平分线,
∴点B关于直线MN的对称点为点A,AD与MN的交点为E,
此时BE+DE的值最小
∴AD的长为BE+ED的最小值,
∴△BDE的周长最小值=
故答案为11.
解答题
16.【解析】如图,作点A关于燃气管道L的对称点A′,连接A′B交L于点P,即点P即为所求.
17.【答案】(1)见解析;(2)见解析
【分析】(1)要使PA+PB最短,根据同一平面内线段最短,可知要作点A关于直线l的对称点A′,连接A′B交直线l于P;
(2)在直线l上任取另一点Q,连接PA、QA、QB.根据轴对称的性质得到PA=PA′,QA=QA′.根据三角形的三边关系即可得到结论.
【详解】(1)如图,点P即为所求.
(2)如图,在直线l上任取一点Q,连接.
∵点A与关于直线l对称,点P,Q在直线l上,
∴.
∵,
∴,即,
∴.
18.【答案】见解析
【分析】利用关于直线对称点的性质得出 P 点关于AB的对称点 P ',以及 P 点关于 CB 的对称点 P ",根据两点直接线段最短,连接 P ' P "即可得出.
【详解】如图所示:C、D点即为所求.
19.【答案】(1)图见解析,C1(-1,2);(2)P(,0),.
【分析】(1)根据轴对称的定义,将关于y轴的对应点分别画出,顺次连接即可;
(2)作点A关于x轴的对称点,与C1连接,此时与x轴的交点即为点P,求出直线的解析式,令y=0,求出x,即可求出点P的坐标,为最小值,利用勾股定理即可求出长度.
【详解】(1)△ABC关于y轴对称的△A1B1C1如图所示:
点C1的坐标(-1,2)
(2)作点A关于x轴的对称点,与C1连接,此时与x轴的交点即为点P,为最小值
∵C1(-1,2),(4,-1)
设的解析式为y=kx+b,将点C1和代入,得:
,求得
∴的解析式为
令y=0,x=,即点P(,0)
利用勾股定理,=.
20.【答案】(1)图见解析;(2)5.5
【分析】(1)根据三角形周长公式和两点之间线段最短来分析,进而再利用简单的作图方法即可作图;
(2)根据三角形面积公式求出AD,再根据中点定义求出BD即可求解.
【详解】(1)如图所示;连接AM,
∵EF是AB的线段垂直平分线
∴AM=BM
∴△BDM的周长=BM+DM+BD
又AM=BM
∴△BDM的周长=AM+DM+BD
∵BD是定值
∴当A、M、D三点在一条直线上时,AM+DM值最小,即△BDM的周长最小,
(2)∵△ABC是等腰三角形
又点D为BC边上的中点,
∴AD是△ABC BC边上的高,
∵,,的面积是,
∴BD=1.5cm,AD=4cm
∴△BDM的周长最小值=AM+DM+BD=AD+BD=5.5cm
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
人教版八年级上册数学 13.4最短路径问题 同步练习
(考试时间:60分钟 满分:100分)
选择题(本大题共10小题,每小题3分,共30分。下列各题的备选答案中,只有一项是最符合题意的,请选出。)
1.直线l是一条河,P,Q是两个村庄.欲在L上的某处修建一个水泵站,向P,Q两地供水,现有如下四种铺设方案,图中实线表示铺设的管道,则所需管道最短的是
A. B.
C. D.
2.A、B是直线l上的两点,P是直线l上的任意一点,要使PA+PB的值最小,那么点P的位置应在
A.线段AB上 B.线段AB的延长线上
C.线段AB的反向延长线上 D.直线l上
3.如图,在中,点、、的坐标分别为、和,则当的周长最小时,的值为( )
A.0 B.1 C.2 D.3
4.如图,是等边三角形,是边上的高,E是的中点,P是上的一个动点,当与的和最小时,的度数是( )
A. B. C. D.
5.如图,△ABC是等边三角形,AD是BC边上的高,E是AC的中点,P是AD上的一个动点,当PC与PE的和最小时,∠ACP的度数是( )
A.30° B.45° C.60° D.90°
6.在中,,,于点,且,若点在边上移动,则的最小值是( )
A.4.5 B.4.6 C.4.7 D.4.8
7.如图,在锐角△ABC中,AB=AC=10,S△ABC =25,∠BAC的平分线交BC于点D,点M,N分别是AD和AB上的动点,则BM+MN的最小值是( )
A.4 B. C.5 D.6
8.已知点A,B是两个居民区的位置,现在准备在墙l边上建立一个垃圾站点P,如图是4位设计师给出的规划图,其中PA+PB距离最短的是()
A. B.
C. D.
9.如图,直线m表示一条河,M,N表示两个村庄,欲在m上的某处修建一个给水站,向两个村庄供水,现有如图所示的四种铺设管道的方案,图中实线表示铺设的管道,则所需管道最短的方案是( )
A. B.
C. D.
10.如图,在△ABC中,∠ACB=90°,以AC为底边在△ABC外作等腰△ACD,过点D作∠ADC的平分线分别交AB,AC于点E,F.若AC=12,BC=5,△ABC的周长为30,点P是直线DE上的一个动点,则△PBC周长的最小值为( )
A.15 B.17 C.18 D.20
填空题(本大题共5小题,每小题4分,共20分。)
11.已知,如图△ABC为等边三角形,高AH=10 cm,P为AH上一动点,D为AB的中点,则PD+PB的最小值为__________cm.
12.如图,在锐角中,,边上有一定点分别是和边上的动点,当的周长最小时,的度数是_________.
13.如图,在平面直角坐标系xOy中,点A的坐标为(0,6),点B为x轴上一动点,以AB为边在直线AB的右侧作等边三角形ABC.若点P为OA的中点,连接PC,则PC的长的最小值为_____.
14.如图,等边△ABC的边长为4,点D在边AC上,AD=1.
(1)△ABC的周长等于_____;
(2)线段PQ在边BA上运动,PQ=1,BQ>BP,连接QD,PC,当四边形PCDQ的周长取得最小值时,请在如图所示的矩形区域内,用无刻度的直尺和圆规,画出线段PC,QD,并简要说明点P和点Q的位置是如何找到的(保留作图痕迹,不要求证明)_____.
15.如图,等腰△ABC底边BC的长为6cm,面积是24cm2,腰AB的垂直平分线MN交AB于点M,交AC于点N,若D为BC边上的中点,E为线段MN上一动点,则△BDE的周长最小值为____cm.
三、解答题(本大题共5小题,每小题10分,共50分。解答应写出文字说明、证明过程或演算步骤.)
16.要在燃气管道L上修建一个泵站P,分别向A,B两镇供气,泵站修在管道的什么地方,可使所用的输气管线最短?在图上画出P点位置,不写作法,保留痕迹.
17.如图,小明在A处放牛,要到河边(直线l)给牛喝水,喝完水把牛赶回家中B处.
(1)要使路程最短,应该在河边哪处给牛喝水,请在直线l上画出喝水处点P的位置;
(2)在直线l上任取一点Q(点Q不与点P重合),连接,试说明.
18.如图,BA、BC是两条公路,在两条公路夹角内部的点P处有一油库,若在两公路上分别建个加油站,并使运油的油罐车从油库出发先到一加油站,再到另一加油站,最后回到油库的路程最短,则加油站应如何选址?
19.如图,平面直角坐标系中,△ABC的顶点坐标分别为A(4,1),B(3,4),C(1,2).
(1)画出△ABC关于y轴对称的△A1B1C1,并写出顶点C1的坐标;
(2)若点P在x轴上,且满足PA+PC1最小,求点P的坐标及PA+PC1的最小值.
20.如图,在等腰三角形ABC中,底边,的面积是,腰AB的垂直平分线EF分别交AB、AC于点E、F,点D为BC边上的中点,M为EF上的动点.
(1)当周长的最小时,请在图中作出满足条件的(保留作图痕迹,不要求写出画法).
(2)周长的最小值是___________.
参考答案
选择题
1.【答案】D
【解析】本题的依据就是两点之间线段最短.首先作点P关于直线l的对称点P′,连接P′Q就是最短的路程.故选D.
2.【答案】A
3.【答案】C
【分析】做出B关于x轴对称点为B′,连接B′C,交x轴于点A',此时的周长最小,由等腰直角三角形的性质可求∠OB'A'=∠OA'B'=45°,可求OB'=OA'=1,即可求解.
【详解】如图所示,做出B关于x轴对称点为B′,连接B′C,交x轴于点A',此时△ABC周长最小
过点C作CH⊥x轴,过点B'作B'H⊥y轴,交CH于H,
∵B(0,2),
∴B′(0,-2),
∵C(5,3),
∴CH= B′H=5,
∴∠CB'H=45°,
∴∠BB' A'=45°,
∴∠OB'A'=∠OA'B'=45°,
∴OB'=OA'=2,
则此时A'坐标为(2,0).
m的值为2.
故选:C.
4.【答案】A
【分析】连接BE,则BE的长度即为PE与PC和的最小值.再利用等边三角形的性质可得∠PBC=∠PCB=30°,即可解决问题;
【详解】如连接BE,与AD交于点P,此时PE+PC最小,
∵△ABC是等边三角形,AD⊥BC,
∴PC=PB,
∴PE+PC=PB+PE=BE,
即BE就是PE+PC的最小值,
∵△ABC是等边三角形,
∴∠BCE=60°,
∵BA=BC,AE=EC,
∴BE⊥AC,
∴∠BEC=90°,
∴∠EBC=30°,
∵PB=PC,
∴∠PCB=∠PBC=30°,
∴∠ECP=∠ACB-∠PCB=30°,
故选:A.
5.【答案】A
【分析】连接BE,则BE的长度即为PE与PC和的最小值.再利用等边三角形的性质可得∠PBC=∠PCB=30°,即可解决问题;
【详解】如图,连接BE,与AD交于点P,此时PE+PC最小,
∵△ABC是等边三角形,AD⊥BC,
∴PC=PB,
∴PE+PC=PB+PE=BE,
即BE就是PE+PC的最小值,
∵△ABC是等边三角形,
∴∠BCE=60°,
∵BA=BC,AE=EC,
∴BE⊥AC,
∴∠BEC=90°,
∴∠EBC=30°,
∵PB=PC,
∴∠PCB=∠PBC=30°,
∴∠ACP =30°,
故选:A.
6.【答案】D
【分析】根据最短路径问题得:当BP⊥AC时,的值最小,利用面积关系得到,代入数值求出答案.
【详解】由题意得:当BP⊥AC时,的值最小,
∵,
∴,
解得BP=,
故选:D.
7.【答案】C
【分析】根据AD是∠BAC的平分线,AB=AC可得出确定出点B关于AD的对称点为点C,根据垂线段最短,过点C作CN⊥AB于N交AD于M,根据轴对称确定最短路线问题,点M即为使BM+MN最小的点,CN=BM+MN,利用三角形的面积求出CN,从而得解.
【详解】如图,∵AD是∠BAC的平分线,AB=AC,
∴点B关于AD的对称点为点C,
过点C作CN⊥AB于N交AD于M,
由轴对称确定最短路线问题,点M即为使BM+MN最小的点,CN=BM+MN,
∵AB=10,S△ABC=25,
∴×10 CN=25,
解得CN=5,
即BM+MN的最小值是5.
故选:C.
8.【答案】D
【分析】根据轴对称的性质以及线段的性质可得到结论.
【详解】根据题意知,在墙l边上建立一个垃圾站点P,使PA+PB距离最小,则作A或者B关于l的对称点,然后连接找到点P,则D选项符合要求.
故选:D
9.【答案】D
【分析】本题可通过找点M或点N关于直线m的对称点,继而利用两点之间线段最短确定最短路径.
【详解】作点M关于直线m的对称点,连接交直线m于P,则P处即为给水站位置.根据“两点之间,线段最短”可排除、、选项,可知选项管道最短.
故选:.
10.【答案】C
【分析】根据点与点关于对称,即可得出,当点与点重合时,,此时的周长最小,根据与的长即可得到周长的最小值.
【详解】是以为底边的等腰三角形,平分,
垂直平分,
点与点关于对称,
,
如图所示,当点与点重合时,,
此时的周长最小,
,,的周长为30,
,
周长的最小值为,
故选:.
填空题
11.【答案】10
【解析】如图,连接PC,
∵△ABC为等边三角形,D为AB的中点,
∴CD⊥AB,
∴CD=AH=10 cm.
∵AH⊥BC,∴PB=PC,
∴PD+PB的最小值为:PD+PB=PC+PD=CD=AH=10 cm.
故答案为:10.
12.【答案】80°
【分析】根据对称的性质,易求得∠C+∠EPF=180°,由 ∠ACB=50°,易求得∠D+∠G=50°,继而求得答案;
【详解】∵ PD⊥AC,PG⊥BC,
∴∠PEC=∠PFC=90°,
∴ ∠C+∠EPF=180°,
∵∠C=50°,
∵∠D+∠G+∠EPF=180°,
∴ ∠D+∠G=50°,
由对称可知:∠G=∠GPN,∠D=∠DPM, L
∴∠GPN+∠DPM=50°,
∴∠MPN=130°-50°=80°,
故答案为:80°.
13.【答案】
【分析】以AP为边作等边三角形APE,连接BE,过点E作EF⊥AP于F,由“SAS”可证△ABE≌△ACP,可得BE=PC,则当BE有最小值时,PC有最小值,即可求解.
【详解】如图,以AP为边作等边三角形APE,连接BE,过点E作EF⊥AP于F,
∵点A的坐标为(0,6),
∴OA=6,
∵点P为OA的中点,
∴AP=3,
∵△AEP是等边三角形,EF⊥AP,
∴AF=PF=,AE=AP,∠EAP=∠BAC=60°,
∴∠BAE=∠CAP,
在△ABE和△ACP中,
∴△ABE≌△ACP(SAS),
∴BE=PC,
∴当BE有最小值时,PC有最小值,
即BE⊥x轴时,BE有最小值,
∴BE的最小值为OF=OP+PF=3+=,
∴PC的最小值为,
故答案为.
14.【答案】12 见解析,过点C作CE∥AB,且CE=1,作点D关于AB的对称点F,连接EF交AB于一点为Q,在AB上BQ之间截取PQ=1,连接CP、DQ,则四边形PCDQ为所求的周长最小的四边形
【分析】(1)根据三角形周长公式计算;
(2)过点C作CE∥AB,且CE=1,作点D关于AB的对称点F,连接EF交AB于一点为Q,在AB上BQ之间截取PQ=1,连接CP、DQ,则四边形PCDQ为所求的周长最小的四边形.
【详解】(1)△ABC的周长等于,
故答案为:12;
(2)如图:
故答案为:过点C作CE∥AB,且CE=1,作点D关于AB的对称点F,连接EF交AB于一点为Q,在AB上BQ之间截取PQ=1,连接CP、DQ,则四边形PCDQ为所求的周长最小的四边形.
.
15.【答案】11
【分析】连接AD,由于△ABC是等腰三角形,点D是BC边的中点,故AD⊥BC,再根据三角形的面积公式求出AD的长,再根据MN是线段AB的垂直平分线可知,点B关于直线NM的对称点为点A,故AD的长为BE+ED的最小值,由此即可得出结论.
【详解】连接AD,
∵△ABC是等腰三角形,点D是BC边的中点,
∴AD⊥BC,BD=3cm
解得AD=8(cm),
∵MN是线段AB的垂直平分线,
∴点B关于直线MN的对称点为点A,AD与MN的交点为E,
此时BE+DE的值最小
∴AD的长为BE+ED的最小值,
∴△BDE的周长最小值=
故答案为11.
解答题
16.【解析】如图,作点A关于燃气管道L的对称点A′,连接A′B交L于点P,即点P即为所求.
17.【答案】(1)见解析;(2)见解析
【分析】(1)要使PA+PB最短,根据同一平面内线段最短,可知要作点A关于直线l的对称点A′,连接A′B交直线l于P;
(2)在直线l上任取另一点Q,连接PA、QA、QB.根据轴对称的性质得到PA=PA′,QA=QA′.根据三角形的三边关系即可得到结论.
【详解】(1)如图,点P即为所求.
(2)如图,在直线l上任取一点Q,连接.
∵点A与关于直线l对称,点P,Q在直线l上,
∴.
∵,
∴,即,
∴.
18.【答案】见解析
【分析】利用关于直线对称点的性质得出 P 点关于AB的对称点 P ',以及 P 点关于 CB 的对称点 P ",根据两点直接线段最短,连接 P ' P "即可得出.
【详解】如图所示:C、D点即为所求.
19.【答案】(1)图见解析,C1(-1,2);(2)P(,0),.
【分析】(1)根据轴对称的定义,将关于y轴的对应点分别画出,顺次连接即可;
(2)作点A关于x轴的对称点,与C1连接,此时与x轴的交点即为点P,求出直线的解析式,令y=0,求出x,即可求出点P的坐标,为最小值,利用勾股定理即可求出长度.
【详解】(1)△ABC关于y轴对称的△A1B1C1如图所示:
点C1的坐标(-1,2)
(2)作点A关于x轴的对称点,与C1连接,此时与x轴的交点即为点P,为最小值
∵C1(-1,2),(4,-1)
设的解析式为y=kx+b,将点C1和代入,得:
,求得
∴的解析式为
令y=0,x=,即点P(,0)
利用勾股定理,=.
20.【答案】(1)图见解析;(2)5.5
【分析】(1)根据三角形周长公式和两点之间线段最短来分析,进而再利用简单的作图方法即可作图;
(2)根据三角形面积公式求出AD,再根据中点定义求出BD即可求解.
【详解】(1)如图所示;连接AM,
∵EF是AB的线段垂直平分线
∴AM=BM
∴△BDM的周长=BM+DM+BD
又AM=BM
∴△BDM的周长=AM+DM+BD
∵BD是定值
∴当A、M、D三点在一条直线上时,AM+DM值最小,即△BDM的周长最小,
(2)∵△ABC是等腰三角形
又点D为BC边上的中点,
∴AD是△ABC BC边上的高,
∵,,的面积是,
∴BD=1.5cm,AD=4cm
∴△BDM的周长最小值=AM+DM+BD=AD+BD=5.5cm
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
