2023-2024学年广东省河源市七年级(下)期末数学试卷(含答案)
文档属性
| 名称 | 2023-2024学年广东省河源市七年级(下)期末数学试卷(含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 703.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-17 00:00:00 | ||
图片预览




文档简介
2023-2024学年广东省河源市七年级(下)期末数学试卷
一、选择题(本大题共10小题,每小题3分,共30分)
1.(3分)如图,∠1的同位角是( )
A.∠2 B.∠3 C.∠4 D.∠5
2.(3分)下列手机中的图标是轴对称图形的是( )
A. B.
C. D.
3.(3分)很多人可能都知道蓝鲸是迄今发现的地球上最大的动物,却都不了解体积最小的动物,世界上体积最小的动物要比蚂蚁小很多倍,它是被命名为H39的原生动物,它的最长直径也不过才0.0000003米.其中数据0.0000003用科学记数法表示为( )
A.0.3×10﹣6 B.3×10﹣6 C.3×10﹣7 D.3×107
4.(3分)下列运算正确的是( )
A.x6÷x3=x2 B.(x3)2=x5 C.x3 x4=x7 D.x3+x3=x6
5.(3分)如果一个角的余角是38°,那么这个角的度数是( )
A.42° B.52° C.142° D.152°
6.(3分)如图是淇淇在超市购买圣女果的销售标签,则在单价、质量、总价的关系中,常量是( )
圣女果单价:8.60元/千克质量:2千克总价:17.2元
A.总价 B.质量
C.单价 D.单价和质量
7.(3分)如图,下列能判定AB∥CD的条件有( )
①∠B+∠BCD=180°;
②∠1=∠2;
③∠3=∠4;
④∠B=∠5.
A.1个 B.2个 C.3个 D.4个
8.(3分)如图,在△ABC中,AD是高,AE是角平分线,AF是中线,则下列说法中错误的是( )
A.BF=CF B.∠C+∠CAD=90°
C.∠BAF=∠CAF D.S△ABC=2S△ABF
9.(3分)甲、乙两队举行了一年一度的赛龙舟比赛,两队在比赛时的路程s(米)与时间t(分钟)之间的函数关系图象如图所示,请你根据图象判断下列说法正确的是( )
A.甲队率先到达终点
B.乙队比甲队少用0.2分钟
C.甲队比乙队多走了200米路程
D.比赛过程中乙队的速度一直比甲队的速度快
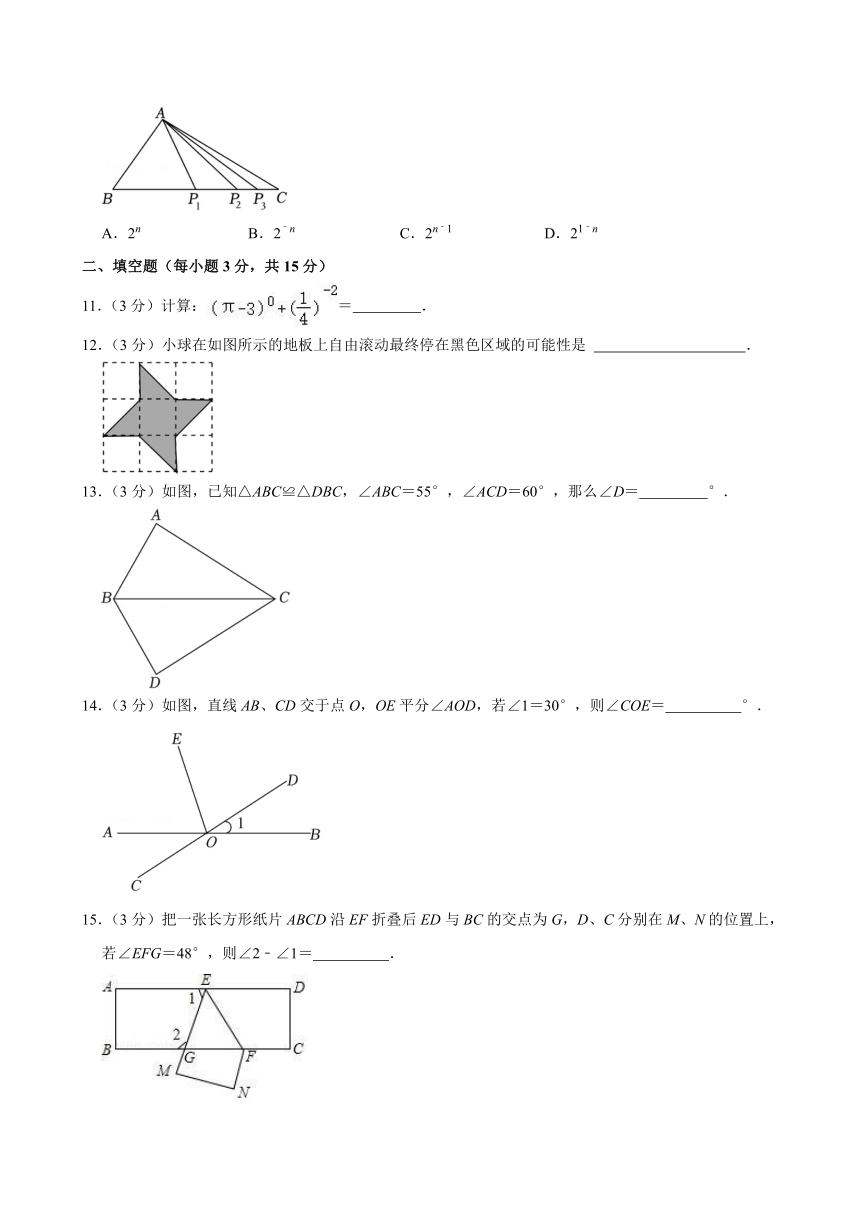
10.(3分)如图,AP1为△ABC的中线,AP2为△AP1C的中线,AP3为△AP2C的中线,…,按此规律,APn+1为△APnC的中线,若△ABP1的面积为1,则△APnC的面积为( )
A.2n B.2﹣n C.2n﹣1 D.21﹣n
二、填空题(每小题3分,共15分)
11.(3分)计算:= .
12.(3分)小球在如图所示的地板上自由滚动最终停在黑色区域的可能性是 .
13.(3分)如图,已知△ABC≌△DBC,∠ABC=55°,∠ACD=60°,那么∠D= °.
14.(3分)如图,直线AB、CD交于点O,OE平分∠AOD,若∠1=30°,则∠COE= °.
15.(3分)把一张长方形纸片ABCD沿EF折叠后ED与BC的交点为G,D、C分别在M、N的位置上,若∠EFG=48°,则∠2﹣∠1= .
三、解答题(本大题共9小题,共75分)
16.(5分)利用平方差公式计算:103×97.
17.(5分)已知:线段a,c,∠α.
求作:△ABC.使BC=a,AB=c,∠ABC=∠α.
18.(7分)先化简,再求值:xy(3xy+2y2)﹣14x3y4÷7xy2,其中x=2,y=﹣1.
19.(7分)小亮和妈妈去超市买凳子,小亮发现把凳子按如图方式叠放在一起时,每叠放一个凳子,增加的高度是一样的.如表是叠放凳子的总高度h与凳子数量n的几组对应值.
凳子的数量n(张) 1 2 3 4 …
叠放凳子的总高度h(厘米) 45 50 55 60 …
根据以上信息,回答下列问题:
(1)按照表格所示的规律,当凳子的数量为6时,叠放的凳子总高度为 厘米;
(2)按照表格所示的规律,写出叠放的凳子总高度h与凳子的数量n之间的关系式 ;
(3)按照表格所示的规律,若将该种凳子按如图方式叠放在层高为92厘米的超市货架上,能叠放11张凳子吗?说明理由.
20.(9分)如图,有一个可以自由转动的转盘,转盘被平均分成6等份,每个扇形区域内分别标有3,4,5,6,7,8这六个数字,转动转盘,当转盘停止转动后,指针指向的数字即为转出的数字.
请回答下列问题:
(1)随机转动转盘,转出数字1是 事件,转出数字8是 事件;(从“随机”,“必然”,“不可能”中选一个填空)
(2)随机转动转盘,转出的数字是奇数的概率是 ;
(3)现有两张分别写有3和4的卡片,随机转动转盘,转盘停止转动后,将转出的数字与两张卡片上的数字分别作为三条线段的长度,则这三条线段能构成三角形的概率是多少?请说明理由.
21.(9分)如图,已知CF是∠ACB的平分线,交AB于点F,点D、E、G分别是AC、AB、BC上的点,且∠3=∠ACB,∠4+∠5=180°.
(1)图中∠2与∠5是一对 ,∠3与∠4是一对 ;(填“同位角”或“内错角”或“同旁内角”)
(2)若CF⊥AB,垂足为F,∠A=58°,则∠4的度数为 ;
(3)判断CF与DE是什么位置关系?说明理由.(请补充完整下面的推理过程)
解:CF DE,理由如下:
∵∠3=∠ACB,(已知)
∴ ,(同位角相等,两直线平行)
∴∠2=∠4,( )
∵∠4+∠5=180°,(已知)
∴ ,(等量代换)
∴ .( )
22.(9分)如图,在△ABC中,D为AB上一点,E为AC中点,连接DE并延长至点F,使得CF∥AB.
(1)求证:△AED≌△CEF;
(2)连接BE,若BE平分∠ABC,CA平分∠BCF,且∠ABE=25°,求∠A的度数.
23.(12分)阅读理解:
若x满足(30﹣x)(x﹣20)=16,求(30﹣x)2+(x﹣20)2的值.
解:设30﹣x=a,x﹣20=b,
则(30﹣x)(x﹣20)=ab=16,
a+b=(30﹣x)+(x﹣20)=10,
∴(30﹣x)2+(x﹣20)2=a2+b2=(a+b)2﹣2ab=102﹣2×16=68
(1)【类比探究】若x满足(280﹣x)(x﹣250)=200.求(280﹣x)2+(x﹣250)2的值;
(2)【联系拓展】若x满足(2024﹣x)(2020﹣x)=5,则(2024﹣x)2+(2020﹣x)2= ;(直接写出结论,不用说明理由.)
(3)【解决问题】如图,在长方形ABCD中,AB=20,BC=12,点E、F是BC、CD上的点,且BE=DF=x,分别以FC、CE为边在长方形ABCD外侧作正方形CFGH和正方形CEMN,若长方形CEPF的面积为180平方单位,则图中阴影部分的面积和为多少平方单位?
24.(12分)综合与实践:数学社团的同学以“两条平行线(AB、CD)和一块含45°角的直角三角板(∠EFG=90°)“为主题开展数学活动,已知点E、F不能同时落在直线AB和CD之间.
(1)【探究】如图1,把三角板的45°角的顶点E、G分别放在AB、CD上,若∠BEG=140°,求∠FGC的度数;
(2)【迁移】如图2,把三角板的锐角顶点G放在CD上,且保持不动,绕点G转动三角板,若点E恰好落在AB和CD之间,且AB与EF所夹锐角为25°,求∠FGC的度数;
(3)【拓展】把三角板的锐角顶点G放在CD上,在绕点G旋转三角板的过程中,若(∠DGE<45°),请直接写出射线GF与AB相交所夹锐角的度数.
2023-2024学年广东省河源市七年级(下)期末数学试卷
参考答案
一、选择题(本大题共10小题,每小题3分,共30分)
1.(3分)如图,∠1的同位角是( )
A.∠2 B.∠3 C.∠4 D.∠5
选:C.
2.(3分)下列手机中的图标是轴对称图形的是( )
A. B.
C. D.
选:C.
3.(3分)很多人可能都知道蓝鲸是迄今发现的地球上最大的动物,却都不了解体积最小的动物,世界上体积最小的动物要比蚂蚁小很多倍,它是被命名为H39的原生动物,它的最长直径也不过才0.0000003米.其中数据0.0000003用科学记数法表示为( )
A.0.3×10﹣6 B.3×10﹣6 C.3×10﹣7 D.3×107
选:C.
4.(3分)下列运算正确的是( )
A.x6÷x3=x2 B.(x3)2=x5 C.x3 x4=x7 D.x3+x3=x6
【分析】根据相关运算法则逐一判断即可.
选:C.
5.(3分)如果一个角的余角是38°,那么这个角的度数是( )
A.42° B.52° C.142° D.152°
选:B.
6.(3分)如图是淇淇在超市购买圣女果的销售标签,则在单价、质量、总价的关系中,常量是( )
圣女果单价:8.60元/千克质量:2千克总价:17.2元
A.总价 B.质量
C.单价 D.单价和质量
选:C.
7.(3分)如图,下列能判定AB∥CD的条件有( )
①∠B+∠BCD=180°;
②∠1=∠2;
③∠3=∠4;
④∠B=∠5.
A.1个 B.2个 C.3个 D.4个
选:C.
8.(3分)如图,在△ABC中,AD是高,AE是角平分线,AF是中线,则下列说法中错误的是( )
A.BF=CF B.∠C+∠CAD=90°
C.∠BAF=∠CAF D.S△ABC=2S△ABF
选:C.
9.(3分)甲、乙两队举行了一年一度的赛龙舟比赛,两队在比赛时的路程s(米)与时间t(分钟)之间的函数关系图象如图所示,请你根据图象判断下列说法正确的是( )
A.甲队率先到达终点
B.乙队比甲队少用0.2分钟
C.甲队比乙队多走了200米路程
D.比赛过程中乙队的速度一直比甲队的速度快
选:B.
10.(3分)如图,AP1为△ABC的中线,AP2为△AP1C的中线,AP3为△AP2C的中线,…,按此规律,APn+1为△APnC的中线,若△ABP1的面积为1,则△APnC的面积为( )
A.2n B.2﹣n C.2n﹣1 D.21﹣n
选:D.
二、填空题(每小题3分,共15分)
11.(3分)计算:= 17 .
12.(3分)小球在如图所示的地板上自由滚动最终停在黑色区域的可能性是 .
13.(3分)如图,已知△ABC≌△DBC,∠ABC=55°,∠ACD=60°,那么∠D= 95 °.
14.(3分)如图,直线AB、CD交于点O,OE平分∠AOD,若∠1=30°,则∠COE= 105 °.
15.(3分)把一张长方形纸片ABCD沿EF折叠后ED与BC的交点为G,D、C分别在M、N的位置上,若∠EFG=48°,则∠2﹣∠1= 12° .
三、解答题(本大题共9小题,共75分)
16.(5分)利用平方差公式计算:103×97.
【解答】解:103×97
=(100+3)×(100﹣3)
=102﹣32
=10000﹣9
=9991.
17.(5分)已知:线段a,c,∠α.
求作:△ABC.使BC=a,AB=c,∠ABC=∠α.
【解答】解:如图所示:①先画射线BC,
②以α的顶点为圆心,任意长为半径画弧,分别交α的两边交于为A′,C′;
③以相同长度为半径,B为圆心,画弧,交BC于点F,以F为圆心,C′A′为半径画弧,交于点E;
④在BF上取点C,使CB=a,以B为圆心,c为半径画圆交BE的延长线于点A,连接AC,
结论:△ABC即为所求三角形.
18.(7分)先化简,再求值:xy(3xy+2y2)﹣14x3y4÷7xy2,其中x=2,y=﹣1.
【解答】解:原式=3x2y2+2xy3﹣2x2y2
=(3﹣2)3x2y2+2xy3
=x2y2+2xy3,
当x=2,y=﹣1时,原式=22×(﹣1)2+2×2×(﹣1)3=4﹣4=0.
19.(7分)小亮和妈妈去超市买凳子,小亮发现把凳子按如图方式叠放在一起时,每叠放一个凳子,增加的高度是一样的.如表是叠放凳子的总高度h与凳子数量n的几组对应值.
凳子的数量n(张) 1 2 3 4 …
叠放凳子的总高度h(厘米) 45 50 55 60 …
根据以上信息,回答下列问题:
(1)按照表格所示的规律,当凳子的数量为6时,叠放的凳子总高度为 70 厘米;
(2)按照表格所示的规律,写出叠放的凳子总高度h与凳子的数量n之间的关系式 h=5n+40(n是正整数) ;
(3)按照表格所示的规律,若将该种凳子按如图方式叠放在层高为92厘米的超市货架上,能叠放11张凳子吗?说明理由.
【解答】解:(1)由表格中的数据可知,凳子数量每增加1,叠放凳子的总高度就增加5,
∴当凳子的数量为6时,叠放的凳子总高度为60+5×(6﹣4)=70(厘米),
故答案为:70;
(2)由题意得:h=5×(n﹣1)+45=5n+40;
故答案为:h=5n+40(n是正整数);
(3)不能叠放11个.理由如下:
当n=11时,h=5×11+40=95,
∵95>92,
∴不能叠放11个.
20.(9分)如图,有一个可以自由转动的转盘,转盘被平均分成6等份,每个扇形区域内分别标有3,4,5,6,7,8这六个数字,转动转盘,当转盘停止转动后,指针指向的数字即为转出的数字.
请回答下列问题:
(1)随机转动转盘,转出数字1是 不可能 事件,转出数字8是 随机 事件;(从“随机”,“必然”,“不可能”中选一个填空)
(2)随机转动转盘,转出的数字是奇数的概率是 ;
(3)现有两张分别写有3和4的卡片,随机转动转盘,转盘停止转动后,将转出的数字与两张卡片上的数字分别作为三条线段的长度,则这三条线段能构成三角形的概率是多少?请说明理由.
【解答】解:(1)随机转动转盘,转出数字1是不可能事件,转出数字8是随机事件;
故答案为:不可能,随机;
(2)随机转动转盘,转出的数字是奇数的概率是==;
故答案为:;
(3)画树状图为:
共有6种等可能的结果,根据三角形的三边关系,其中这三条线段能构成三角形的结果数为4种,
所以这三条线段能构成三角形的概率==.
21.(9分)如图,已知CF是∠ACB的平分线,交AB于点F,点D、E、G分别是AC、AB、BC上的点,且∠3=∠ACB,∠4+∠5=180°.
(1)图中∠2与∠5是一对 同旁内角 ,∠3与∠4是一对 内错角 ;(填“同位角”或“内错角”或“同旁内角”)
(2)若CF⊥AB,垂足为F,∠A=58°,则∠4的度数为 32° ;
(3)判断CF与DE是什么位置关系?说明理由.(请补充完整下面的推理过程)
解:CF ∥ DE,理由如下:
∵∠3=∠ACB,(已知)
∴ AC∥FG ,(同位角相等,两直线平行)
∴∠2=∠4,( 两直线平行,内错角相等 )
∵∠4+∠5=180°,(已知)
∴ ∠2+∠5=180° ,(等量代换)
∴ DE∥CF .( 同旁内角互补,两直线平行 )
【解答】解:(1)图中∠2与∠5是一对同旁内角,∠3与∠4是一对内错角;
故答案为:同旁内角;内错角;
(2)∵CF⊥AB,
∴∠CFA=90°,
∵∠A=58°,
∴∠2=90°﹣∠A=32°,
∵∠3=∠ACB,
∴FG∥AC,
∴∠2=∠4=32°,
故答案为:32°;
(3)CF∥DE,理由如下:
∵∠3=∠ACB,(已知)
∴AC∥FG,(同位角相等,两直线平行)
∴∠2=∠4,(两直线平行,内错角相等)
∵∠4+∠5=180°,(已知)
∴∠2+∠5=180°,(等量代换)
∴DE∥CF.(同旁内角互补,两直线平行)
故答案为:∥;AC∥FG;两直线平行,内错角相等;∠2+∠5=180°;DE∥CF;同旁内角互补,两直线平行.
22.(9分)如图,在△ABC中,D为AB上一点,E为AC中点,连接DE并延长至点F,使得CF∥AB.
(1)求证:△AED≌△CEF;
(2)连接BE,若BE平分∠ABC,CA平分∠BCF,且∠ABE=25°,求∠A的度数.
【解答】(1)证明:∵E为AC中点,
∴AE=CE,
∵CF∥AB.
∴∠A=∠ACF,
在△AED 和△CEF中,
∴△AED≌△CEF(ASA);
(2)解:∵BE 平分∠ABC,∠ABE=25°,
∴∠ABC=2∠ABE=50°,
∵CF∥AB.
∴∠ABC+∠BCF=180°,∠A=∠ACF,
∴∠BCF=180°﹣∠ABC=130°,
∵CA平分∠BCF,
∴,
∴∠A=65°.
23.(12分)阅读理解:
若x满足(30﹣x)(x﹣20)=16,求(30﹣x)2+(x﹣20)2的值.
解:设30﹣x=a,x﹣20=b,
则(30﹣x)(x﹣20)=ab=16,
a+b=(30﹣x)+(x﹣20)=10,
∴(30﹣x)2+(x﹣20)2=a2+b2=(a+b)2﹣2ab=102﹣2×16=68
(1)【类比探究】若x满足(280﹣x)(x﹣250)=200.求(280﹣x)2+(x﹣250)2的值;
(2)【联系拓展】若x满足(2024﹣x)(2020﹣x)=5,则(2024﹣x)2+(2020﹣x)2= 26 ;(直接写出结论,不用说明理由.)
(3)【解决问题】如图,在长方形ABCD中,AB=20,BC=12,点E、F是BC、CD上的点,且BE=DF=x,分别以FC、CE为边在长方形ABCD外侧作正方形CFGH和正方形CEMN,若长方形CEPF的面积为180平方单位,则图中阴影部分的面积和为多少平方单位?
【解答】解:(1)设 280﹣x=a,x﹣250=b,
则 (280﹣x)(x﹣250)=ab=200,
a+b=(280﹣x)+(x﹣250)=30,
所以 (280﹣x)2+(x﹣250)2=a2+b2=(a+b)2﹣2ab=302﹣2×200=500;
(2)设 2024﹣x=a,2020﹣x=b,
则 (x﹣2024)(2020﹣x)=﹣ab=﹣5,
﹣a+b=(x﹣2024)+(2020﹣x)=﹣4,
所以 (2024﹣x)2+(2020﹣x)2=(x﹣2024)2+(2020﹣x)2=(﹣a)2+b2=(﹣a+b)2﹣2ab=(﹣4)2﹣2×(﹣5)=16+10=26,
故答案为:26;
(3)由题意得,FC=(20﹣x),EC=(12﹣x),
∴阴影部分的面积和为 (20﹣x)2+(12﹣x)2,
∵长方形 CEPF 的面积为180,
∴.(20﹣x)(12﹣x)=180,
∴(20﹣x)(x﹣12)=﹣180,
设20﹣x=a,x﹣12=b,
则(20﹣x)(x﹣12)=ab=﹣180,
a+b=(20﹣x)+(x﹣12)=8,
∴(20﹣x)2+(x﹣12)2
=(20﹣x)2+(12﹣x)2
=a2+b2
=(a+b)2﹣2ab
=82﹣2×(﹣180)
=424,
∴阴影部分的面积和为424平方单位.
24.(12分)综合与实践:数学社团的同学以“两条平行线(AB、CD)和一块含45°角的直角三角板(∠EFG=90°)“为主题开展数学活动,已知点E、F不能同时落在直线AB和CD之间.
(1)【探究】如图1,把三角板的45°角的顶点E、G分别放在AB、CD上,若∠BEG=140°,求∠FGC的度数;
(2)【迁移】如图2,把三角板的锐角顶点G放在CD上,且保持不动,绕点G转动三角板,若点E恰好落在AB和CD之间,且AB与EF所夹锐角为25°,求∠FGC的度数;
(3)【拓展】把三角板的锐角顶点G放在CD上,在绕点G旋转三角板的过程中,若(∠DGE<45°),请直接写出射线GF与AB相交所夹锐角的度数.
【解答】解:(1)依题意得:∠FGE=45°,
∵AB∥CD,
∴∠BEG+∠EGD=180°,
∠BEG=140°,
∴∠EGD=180°﹣140°=40°,
∵∠EGF=45°,∠FGC+∠EGF+∠EGD=180°,
∴∠FGC=180°﹣45°﹣40°=95°;
(2)如图2:过点E作EN∥CD,
依题意得:∠BME=25°,∠FEG=∠FGE=45°,
∵AB∥CD,EN∥CD,
∴AB∥EN∥CD,
∴∠NEM=∠BME=25°,
∴∠NEG=∠FEG﹣∠NEM=45°﹣25°=20°,
∴∠DGE=∠NEG=20°,
∴∠FGD=∠FGE+∠DGE=45°+20°=65°,
∴∠FGC=180°﹣∠FGD=180°﹣65°=115°;
(3)射线GF与AB相交所夹锐角的度数为67.5° 或 11.25°;理由如下:
分两种情况讨论如下:
①当点E在CD上方时,设AB交GF于点H,如图3所示:
依题意得:∠FEG=∠FGE=45°,
设∠DGE=α,则∠FGC=5∠DGE=5α,
∵∠DGE+∠FGE+∠FGC=180°,
∴5α+45°+α=180°,
解得:α=22.5°,
∴∠FGC=5α=112.5°,
∵AB∥CD,
∴∠AHG=180°﹣∠FGC=180°﹣112.5°=67.5°;
②当点E在CD下方时,延长GF交AB于点H,如图4所示:
依题意得:∠FGE=45°,
设∠EGD=β,则∠FGC=5∠DGE=5β,
∴∠FGD=∠FGE﹣∠EGD=45°﹣β,
∠FGC+∠FGD=180°,
∴5β+45°﹣β=180°,
解得:β=33.75°,
∴∠FGC=5β=168.75°,
∵AB∥CD,
∠AHG=180°﹣∠FGC=180°﹣168.75°=11.25°,
综上所述:射线GF与AB相交所夹锐角的度数为67.5°或11.25°.
一、选择题(本大题共10小题,每小题3分,共30分)
1.(3分)如图,∠1的同位角是( )
A.∠2 B.∠3 C.∠4 D.∠5
2.(3分)下列手机中的图标是轴对称图形的是( )
A. B.
C. D.
3.(3分)很多人可能都知道蓝鲸是迄今发现的地球上最大的动物,却都不了解体积最小的动物,世界上体积最小的动物要比蚂蚁小很多倍,它是被命名为H39的原生动物,它的最长直径也不过才0.0000003米.其中数据0.0000003用科学记数法表示为( )
A.0.3×10﹣6 B.3×10﹣6 C.3×10﹣7 D.3×107
4.(3分)下列运算正确的是( )
A.x6÷x3=x2 B.(x3)2=x5 C.x3 x4=x7 D.x3+x3=x6
5.(3分)如果一个角的余角是38°,那么这个角的度数是( )
A.42° B.52° C.142° D.152°
6.(3分)如图是淇淇在超市购买圣女果的销售标签,则在单价、质量、总价的关系中,常量是( )
圣女果单价:8.60元/千克质量:2千克总价:17.2元
A.总价 B.质量
C.单价 D.单价和质量
7.(3分)如图,下列能判定AB∥CD的条件有( )
①∠B+∠BCD=180°;
②∠1=∠2;
③∠3=∠4;
④∠B=∠5.
A.1个 B.2个 C.3个 D.4个
8.(3分)如图,在△ABC中,AD是高,AE是角平分线,AF是中线,则下列说法中错误的是( )
A.BF=CF B.∠C+∠CAD=90°
C.∠BAF=∠CAF D.S△ABC=2S△ABF
9.(3分)甲、乙两队举行了一年一度的赛龙舟比赛,两队在比赛时的路程s(米)与时间t(分钟)之间的函数关系图象如图所示,请你根据图象判断下列说法正确的是( )
A.甲队率先到达终点
B.乙队比甲队少用0.2分钟
C.甲队比乙队多走了200米路程
D.比赛过程中乙队的速度一直比甲队的速度快
10.(3分)如图,AP1为△ABC的中线,AP2为△AP1C的中线,AP3为△AP2C的中线,…,按此规律,APn+1为△APnC的中线,若△ABP1的面积为1,则△APnC的面积为( )
A.2n B.2﹣n C.2n﹣1 D.21﹣n
二、填空题(每小题3分,共15分)
11.(3分)计算:= .
12.(3分)小球在如图所示的地板上自由滚动最终停在黑色区域的可能性是 .
13.(3分)如图,已知△ABC≌△DBC,∠ABC=55°,∠ACD=60°,那么∠D= °.
14.(3分)如图,直线AB、CD交于点O,OE平分∠AOD,若∠1=30°,则∠COE= °.
15.(3分)把一张长方形纸片ABCD沿EF折叠后ED与BC的交点为G,D、C分别在M、N的位置上,若∠EFG=48°,则∠2﹣∠1= .
三、解答题(本大题共9小题,共75分)
16.(5分)利用平方差公式计算:103×97.
17.(5分)已知:线段a,c,∠α.
求作:△ABC.使BC=a,AB=c,∠ABC=∠α.
18.(7分)先化简,再求值:xy(3xy+2y2)﹣14x3y4÷7xy2,其中x=2,y=﹣1.
19.(7分)小亮和妈妈去超市买凳子,小亮发现把凳子按如图方式叠放在一起时,每叠放一个凳子,增加的高度是一样的.如表是叠放凳子的总高度h与凳子数量n的几组对应值.
凳子的数量n(张) 1 2 3 4 …
叠放凳子的总高度h(厘米) 45 50 55 60 …
根据以上信息,回答下列问题:
(1)按照表格所示的规律,当凳子的数量为6时,叠放的凳子总高度为 厘米;
(2)按照表格所示的规律,写出叠放的凳子总高度h与凳子的数量n之间的关系式 ;
(3)按照表格所示的规律,若将该种凳子按如图方式叠放在层高为92厘米的超市货架上,能叠放11张凳子吗?说明理由.
20.(9分)如图,有一个可以自由转动的转盘,转盘被平均分成6等份,每个扇形区域内分别标有3,4,5,6,7,8这六个数字,转动转盘,当转盘停止转动后,指针指向的数字即为转出的数字.
请回答下列问题:
(1)随机转动转盘,转出数字1是 事件,转出数字8是 事件;(从“随机”,“必然”,“不可能”中选一个填空)
(2)随机转动转盘,转出的数字是奇数的概率是 ;
(3)现有两张分别写有3和4的卡片,随机转动转盘,转盘停止转动后,将转出的数字与两张卡片上的数字分别作为三条线段的长度,则这三条线段能构成三角形的概率是多少?请说明理由.
21.(9分)如图,已知CF是∠ACB的平分线,交AB于点F,点D、E、G分别是AC、AB、BC上的点,且∠3=∠ACB,∠4+∠5=180°.
(1)图中∠2与∠5是一对 ,∠3与∠4是一对 ;(填“同位角”或“内错角”或“同旁内角”)
(2)若CF⊥AB,垂足为F,∠A=58°,则∠4的度数为 ;
(3)判断CF与DE是什么位置关系?说明理由.(请补充完整下面的推理过程)
解:CF DE,理由如下:
∵∠3=∠ACB,(已知)
∴ ,(同位角相等,两直线平行)
∴∠2=∠4,( )
∵∠4+∠5=180°,(已知)
∴ ,(等量代换)
∴ .( )
22.(9分)如图,在△ABC中,D为AB上一点,E为AC中点,连接DE并延长至点F,使得CF∥AB.
(1)求证:△AED≌△CEF;
(2)连接BE,若BE平分∠ABC,CA平分∠BCF,且∠ABE=25°,求∠A的度数.
23.(12分)阅读理解:
若x满足(30﹣x)(x﹣20)=16,求(30﹣x)2+(x﹣20)2的值.
解:设30﹣x=a,x﹣20=b,
则(30﹣x)(x﹣20)=ab=16,
a+b=(30﹣x)+(x﹣20)=10,
∴(30﹣x)2+(x﹣20)2=a2+b2=(a+b)2﹣2ab=102﹣2×16=68
(1)【类比探究】若x满足(280﹣x)(x﹣250)=200.求(280﹣x)2+(x﹣250)2的值;
(2)【联系拓展】若x满足(2024﹣x)(2020﹣x)=5,则(2024﹣x)2+(2020﹣x)2= ;(直接写出结论,不用说明理由.)
(3)【解决问题】如图,在长方形ABCD中,AB=20,BC=12,点E、F是BC、CD上的点,且BE=DF=x,分别以FC、CE为边在长方形ABCD外侧作正方形CFGH和正方形CEMN,若长方形CEPF的面积为180平方单位,则图中阴影部分的面积和为多少平方单位?
24.(12分)综合与实践:数学社团的同学以“两条平行线(AB、CD)和一块含45°角的直角三角板(∠EFG=90°)“为主题开展数学活动,已知点E、F不能同时落在直线AB和CD之间.
(1)【探究】如图1,把三角板的45°角的顶点E、G分别放在AB、CD上,若∠BEG=140°,求∠FGC的度数;
(2)【迁移】如图2,把三角板的锐角顶点G放在CD上,且保持不动,绕点G转动三角板,若点E恰好落在AB和CD之间,且AB与EF所夹锐角为25°,求∠FGC的度数;
(3)【拓展】把三角板的锐角顶点G放在CD上,在绕点G旋转三角板的过程中,若(∠DGE<45°),请直接写出射线GF与AB相交所夹锐角的度数.
2023-2024学年广东省河源市七年级(下)期末数学试卷
参考答案
一、选择题(本大题共10小题,每小题3分,共30分)
1.(3分)如图,∠1的同位角是( )
A.∠2 B.∠3 C.∠4 D.∠5
选:C.
2.(3分)下列手机中的图标是轴对称图形的是( )
A. B.
C. D.
选:C.
3.(3分)很多人可能都知道蓝鲸是迄今发现的地球上最大的动物,却都不了解体积最小的动物,世界上体积最小的动物要比蚂蚁小很多倍,它是被命名为H39的原生动物,它的最长直径也不过才0.0000003米.其中数据0.0000003用科学记数法表示为( )
A.0.3×10﹣6 B.3×10﹣6 C.3×10﹣7 D.3×107
选:C.
4.(3分)下列运算正确的是( )
A.x6÷x3=x2 B.(x3)2=x5 C.x3 x4=x7 D.x3+x3=x6
【分析】根据相关运算法则逐一判断即可.
选:C.
5.(3分)如果一个角的余角是38°,那么这个角的度数是( )
A.42° B.52° C.142° D.152°
选:B.
6.(3分)如图是淇淇在超市购买圣女果的销售标签,则在单价、质量、总价的关系中,常量是( )
圣女果单价:8.60元/千克质量:2千克总价:17.2元
A.总价 B.质量
C.单价 D.单价和质量
选:C.
7.(3分)如图,下列能判定AB∥CD的条件有( )
①∠B+∠BCD=180°;
②∠1=∠2;
③∠3=∠4;
④∠B=∠5.
A.1个 B.2个 C.3个 D.4个
选:C.
8.(3分)如图,在△ABC中,AD是高,AE是角平分线,AF是中线,则下列说法中错误的是( )
A.BF=CF B.∠C+∠CAD=90°
C.∠BAF=∠CAF D.S△ABC=2S△ABF
选:C.
9.(3分)甲、乙两队举行了一年一度的赛龙舟比赛,两队在比赛时的路程s(米)与时间t(分钟)之间的函数关系图象如图所示,请你根据图象判断下列说法正确的是( )
A.甲队率先到达终点
B.乙队比甲队少用0.2分钟
C.甲队比乙队多走了200米路程
D.比赛过程中乙队的速度一直比甲队的速度快
选:B.
10.(3分)如图,AP1为△ABC的中线,AP2为△AP1C的中线,AP3为△AP2C的中线,…,按此规律,APn+1为△APnC的中线,若△ABP1的面积为1,则△APnC的面积为( )
A.2n B.2﹣n C.2n﹣1 D.21﹣n
选:D.
二、填空题(每小题3分,共15分)
11.(3分)计算:= 17 .
12.(3分)小球在如图所示的地板上自由滚动最终停在黑色区域的可能性是 .
13.(3分)如图,已知△ABC≌△DBC,∠ABC=55°,∠ACD=60°,那么∠D= 95 °.
14.(3分)如图,直线AB、CD交于点O,OE平分∠AOD,若∠1=30°,则∠COE= 105 °.
15.(3分)把一张长方形纸片ABCD沿EF折叠后ED与BC的交点为G,D、C分别在M、N的位置上,若∠EFG=48°,则∠2﹣∠1= 12° .
三、解答题(本大题共9小题,共75分)
16.(5分)利用平方差公式计算:103×97.
【解答】解:103×97
=(100+3)×(100﹣3)
=102﹣32
=10000﹣9
=9991.
17.(5分)已知:线段a,c,∠α.
求作:△ABC.使BC=a,AB=c,∠ABC=∠α.
【解答】解:如图所示:①先画射线BC,
②以α的顶点为圆心,任意长为半径画弧,分别交α的两边交于为A′,C′;
③以相同长度为半径,B为圆心,画弧,交BC于点F,以F为圆心,C′A′为半径画弧,交于点E;
④在BF上取点C,使CB=a,以B为圆心,c为半径画圆交BE的延长线于点A,连接AC,
结论:△ABC即为所求三角形.
18.(7分)先化简,再求值:xy(3xy+2y2)﹣14x3y4÷7xy2,其中x=2,y=﹣1.
【解答】解:原式=3x2y2+2xy3﹣2x2y2
=(3﹣2)3x2y2+2xy3
=x2y2+2xy3,
当x=2,y=﹣1时,原式=22×(﹣1)2+2×2×(﹣1)3=4﹣4=0.
19.(7分)小亮和妈妈去超市买凳子,小亮发现把凳子按如图方式叠放在一起时,每叠放一个凳子,增加的高度是一样的.如表是叠放凳子的总高度h与凳子数量n的几组对应值.
凳子的数量n(张) 1 2 3 4 …
叠放凳子的总高度h(厘米) 45 50 55 60 …
根据以上信息,回答下列问题:
(1)按照表格所示的规律,当凳子的数量为6时,叠放的凳子总高度为 70 厘米;
(2)按照表格所示的规律,写出叠放的凳子总高度h与凳子的数量n之间的关系式 h=5n+40(n是正整数) ;
(3)按照表格所示的规律,若将该种凳子按如图方式叠放在层高为92厘米的超市货架上,能叠放11张凳子吗?说明理由.
【解答】解:(1)由表格中的数据可知,凳子数量每增加1,叠放凳子的总高度就增加5,
∴当凳子的数量为6时,叠放的凳子总高度为60+5×(6﹣4)=70(厘米),
故答案为:70;
(2)由题意得:h=5×(n﹣1)+45=5n+40;
故答案为:h=5n+40(n是正整数);
(3)不能叠放11个.理由如下:
当n=11时,h=5×11+40=95,
∵95>92,
∴不能叠放11个.
20.(9分)如图,有一个可以自由转动的转盘,转盘被平均分成6等份,每个扇形区域内分别标有3,4,5,6,7,8这六个数字,转动转盘,当转盘停止转动后,指针指向的数字即为转出的数字.
请回答下列问题:
(1)随机转动转盘,转出数字1是 不可能 事件,转出数字8是 随机 事件;(从“随机”,“必然”,“不可能”中选一个填空)
(2)随机转动转盘,转出的数字是奇数的概率是 ;
(3)现有两张分别写有3和4的卡片,随机转动转盘,转盘停止转动后,将转出的数字与两张卡片上的数字分别作为三条线段的长度,则这三条线段能构成三角形的概率是多少?请说明理由.
【解答】解:(1)随机转动转盘,转出数字1是不可能事件,转出数字8是随机事件;
故答案为:不可能,随机;
(2)随机转动转盘,转出的数字是奇数的概率是==;
故答案为:;
(3)画树状图为:
共有6种等可能的结果,根据三角形的三边关系,其中这三条线段能构成三角形的结果数为4种,
所以这三条线段能构成三角形的概率==.
21.(9分)如图,已知CF是∠ACB的平分线,交AB于点F,点D、E、G分别是AC、AB、BC上的点,且∠3=∠ACB,∠4+∠5=180°.
(1)图中∠2与∠5是一对 同旁内角 ,∠3与∠4是一对 内错角 ;(填“同位角”或“内错角”或“同旁内角”)
(2)若CF⊥AB,垂足为F,∠A=58°,则∠4的度数为 32° ;
(3)判断CF与DE是什么位置关系?说明理由.(请补充完整下面的推理过程)
解:CF ∥ DE,理由如下:
∵∠3=∠ACB,(已知)
∴ AC∥FG ,(同位角相等,两直线平行)
∴∠2=∠4,( 两直线平行,内错角相等 )
∵∠4+∠5=180°,(已知)
∴ ∠2+∠5=180° ,(等量代换)
∴ DE∥CF .( 同旁内角互补,两直线平行 )
【解答】解:(1)图中∠2与∠5是一对同旁内角,∠3与∠4是一对内错角;
故答案为:同旁内角;内错角;
(2)∵CF⊥AB,
∴∠CFA=90°,
∵∠A=58°,
∴∠2=90°﹣∠A=32°,
∵∠3=∠ACB,
∴FG∥AC,
∴∠2=∠4=32°,
故答案为:32°;
(3)CF∥DE,理由如下:
∵∠3=∠ACB,(已知)
∴AC∥FG,(同位角相等,两直线平行)
∴∠2=∠4,(两直线平行,内错角相等)
∵∠4+∠5=180°,(已知)
∴∠2+∠5=180°,(等量代换)
∴DE∥CF.(同旁内角互补,两直线平行)
故答案为:∥;AC∥FG;两直线平行,内错角相等;∠2+∠5=180°;DE∥CF;同旁内角互补,两直线平行.
22.(9分)如图,在△ABC中,D为AB上一点,E为AC中点,连接DE并延长至点F,使得CF∥AB.
(1)求证:△AED≌△CEF;
(2)连接BE,若BE平分∠ABC,CA平分∠BCF,且∠ABE=25°,求∠A的度数.
【解答】(1)证明:∵E为AC中点,
∴AE=CE,
∵CF∥AB.
∴∠A=∠ACF,
在△AED 和△CEF中,
∴△AED≌△CEF(ASA);
(2)解:∵BE 平分∠ABC,∠ABE=25°,
∴∠ABC=2∠ABE=50°,
∵CF∥AB.
∴∠ABC+∠BCF=180°,∠A=∠ACF,
∴∠BCF=180°﹣∠ABC=130°,
∵CA平分∠BCF,
∴,
∴∠A=65°.
23.(12分)阅读理解:
若x满足(30﹣x)(x﹣20)=16,求(30﹣x)2+(x﹣20)2的值.
解:设30﹣x=a,x﹣20=b,
则(30﹣x)(x﹣20)=ab=16,
a+b=(30﹣x)+(x﹣20)=10,
∴(30﹣x)2+(x﹣20)2=a2+b2=(a+b)2﹣2ab=102﹣2×16=68
(1)【类比探究】若x满足(280﹣x)(x﹣250)=200.求(280﹣x)2+(x﹣250)2的值;
(2)【联系拓展】若x满足(2024﹣x)(2020﹣x)=5,则(2024﹣x)2+(2020﹣x)2= 26 ;(直接写出结论,不用说明理由.)
(3)【解决问题】如图,在长方形ABCD中,AB=20,BC=12,点E、F是BC、CD上的点,且BE=DF=x,分别以FC、CE为边在长方形ABCD外侧作正方形CFGH和正方形CEMN,若长方形CEPF的面积为180平方单位,则图中阴影部分的面积和为多少平方单位?
【解答】解:(1)设 280﹣x=a,x﹣250=b,
则 (280﹣x)(x﹣250)=ab=200,
a+b=(280﹣x)+(x﹣250)=30,
所以 (280﹣x)2+(x﹣250)2=a2+b2=(a+b)2﹣2ab=302﹣2×200=500;
(2)设 2024﹣x=a,2020﹣x=b,
则 (x﹣2024)(2020﹣x)=﹣ab=﹣5,
﹣a+b=(x﹣2024)+(2020﹣x)=﹣4,
所以 (2024﹣x)2+(2020﹣x)2=(x﹣2024)2+(2020﹣x)2=(﹣a)2+b2=(﹣a+b)2﹣2ab=(﹣4)2﹣2×(﹣5)=16+10=26,
故答案为:26;
(3)由题意得,FC=(20﹣x),EC=(12﹣x),
∴阴影部分的面积和为 (20﹣x)2+(12﹣x)2,
∵长方形 CEPF 的面积为180,
∴.(20﹣x)(12﹣x)=180,
∴(20﹣x)(x﹣12)=﹣180,
设20﹣x=a,x﹣12=b,
则(20﹣x)(x﹣12)=ab=﹣180,
a+b=(20﹣x)+(x﹣12)=8,
∴(20﹣x)2+(x﹣12)2
=(20﹣x)2+(12﹣x)2
=a2+b2
=(a+b)2﹣2ab
=82﹣2×(﹣180)
=424,
∴阴影部分的面积和为424平方单位.
24.(12分)综合与实践:数学社团的同学以“两条平行线(AB、CD)和一块含45°角的直角三角板(∠EFG=90°)“为主题开展数学活动,已知点E、F不能同时落在直线AB和CD之间.
(1)【探究】如图1,把三角板的45°角的顶点E、G分别放在AB、CD上,若∠BEG=140°,求∠FGC的度数;
(2)【迁移】如图2,把三角板的锐角顶点G放在CD上,且保持不动,绕点G转动三角板,若点E恰好落在AB和CD之间,且AB与EF所夹锐角为25°,求∠FGC的度数;
(3)【拓展】把三角板的锐角顶点G放在CD上,在绕点G旋转三角板的过程中,若(∠DGE<45°),请直接写出射线GF与AB相交所夹锐角的度数.
【解答】解:(1)依题意得:∠FGE=45°,
∵AB∥CD,
∴∠BEG+∠EGD=180°,
∠BEG=140°,
∴∠EGD=180°﹣140°=40°,
∵∠EGF=45°,∠FGC+∠EGF+∠EGD=180°,
∴∠FGC=180°﹣45°﹣40°=95°;
(2)如图2:过点E作EN∥CD,
依题意得:∠BME=25°,∠FEG=∠FGE=45°,
∵AB∥CD,EN∥CD,
∴AB∥EN∥CD,
∴∠NEM=∠BME=25°,
∴∠NEG=∠FEG﹣∠NEM=45°﹣25°=20°,
∴∠DGE=∠NEG=20°,
∴∠FGD=∠FGE+∠DGE=45°+20°=65°,
∴∠FGC=180°﹣∠FGD=180°﹣65°=115°;
(3)射线GF与AB相交所夹锐角的度数为67.5° 或 11.25°;理由如下:
分两种情况讨论如下:
①当点E在CD上方时,设AB交GF于点H,如图3所示:
依题意得:∠FEG=∠FGE=45°,
设∠DGE=α,则∠FGC=5∠DGE=5α,
∵∠DGE+∠FGE+∠FGC=180°,
∴5α+45°+α=180°,
解得:α=22.5°,
∴∠FGC=5α=112.5°,
∵AB∥CD,
∴∠AHG=180°﹣∠FGC=180°﹣112.5°=67.5°;
②当点E在CD下方时,延长GF交AB于点H,如图4所示:
依题意得:∠FGE=45°,
设∠EGD=β,则∠FGC=5∠DGE=5β,
∴∠FGD=∠FGE﹣∠EGD=45°﹣β,
∠FGC+∠FGD=180°,
∴5β+45°﹣β=180°,
解得:β=33.75°,
∴∠FGC=5β=168.75°,
∵AB∥CD,
∠AHG=180°﹣∠FGC=180°﹣168.75°=11.25°,
综上所述:射线GF与AB相交所夹锐角的度数为67.5°或11.25°.
同课章节目录
