第2章 整式及其加减 数学活动 课件(共23张PPT)2024-2025学年沪科版七年级数学上册
文档属性
| 名称 | 第2章 整式及其加减 数学活动 课件(共23张PPT)2024-2025学年沪科版七年级数学上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 8.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-17 20:59:27 | ||
图片预览








文档简介
(共23张PPT)
数学活动
沪科版 七年级上册
进行新课
数学活动
探索规律
探究1:一个两位数,个位上的数字为a,十位上的数字为b.
(1)这两位数可以用代数式表示为_________;
(2)如果a+b能被3整除,那么这个两位数能被3整除吗?
10b+a
(2)如果a+b能被3整除,那么这个两位数能被3整除吗?
解:(10b+a)-(a+b)
=10b+a-a-b
=9b
因为9b能被3整除,a+b能被3整除,
所以9b+(a+b)=10b+a能被3整除,
即这个两位数能被3整除.
去括号
通过分析计算,你发现了什么规律?
如果一个两位数个位上的数字与十位上的数字之和能被3整除,那么这个两位数能被3整除.
探究2:任意写一个三位数,比如 419. 然后把这个三位数重写一次与它并排构成一个六位数,如419419. 对于这个六位数,先用7去除,把得到的商用11去除,对第二次得到的商再用13去除. 这时,你得到怎样的结果?
419419÷7=59917
59917÷11=5447
5447÷13= 419
再写几个三位数,按上述步骤试试,你有什么发现?
例如:
①三位数273,构成的六位数为273273.
273273÷7=39039
39039÷11=3549
3549÷13=273
②三位数648,构成的六位数为648648.
648648÷7=92664
92664÷11=8424
8424÷13=648
你能说明其中的道理吗?
最后得到的数与原三位数相等
对于任意一个三位数,个位上的数字为a,十位上的数字为b,百位上的数字为c.
(1)这个三位数可以用代数式表示为____________.
(2)把这个三位数重写一次与它并排构成一个六位数,则这个六位数可以用代数式表示为__________________________________.
100c+10b+a
100000c+10000b+1000a+100c+10b+a
100000c+10000b+1000a+100c+10b+a
=100100c+10010b+1001a
=1001(100c+10b+a)
原三位数
7×11×13
即这个六位数,先用7去除,把得到的商用11去除,对第二次得到的商再用13去除,最后的结果等于原三位数.
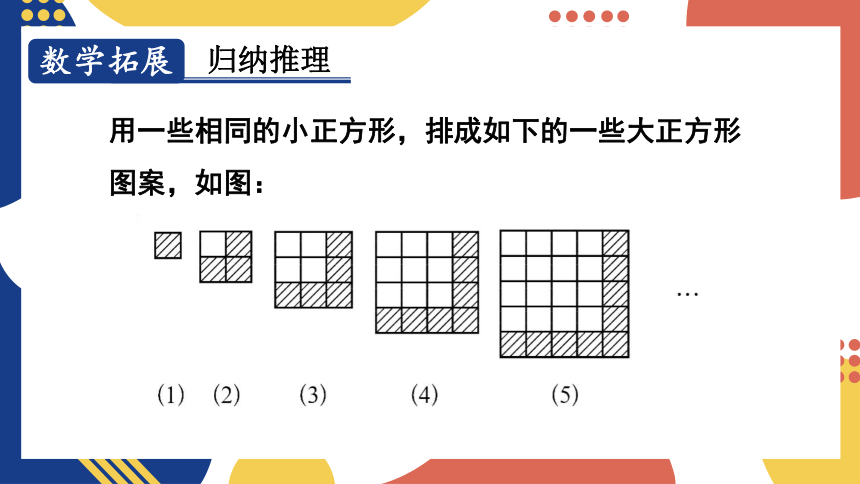
数学拓展
归纳推理
用一些相同的小正方形,排成如下的一些大正方形图案,如图:
1.把每个图中一边上的小正方形个数和有阴影的小正方形的个数填入表中:
图号(n) 1 2 3 4 5 … k …
一边上小正方形个数(n) 1 2 3 … …
阴影小正方形个数(an) 1 3 5 … …
4
5
7
9
k
2k-1
2. 第1个图中小正方形只有1个,且有阴影,记作S1=1.把第1个图并入第2个图,这时第2个图中阴影小正方形数就是前面两个图中阴影小正方形数的和:a1+a2=1+3=4.我们把这个和a1+a2记作S2,即
S2=a1+a2=1+3=22.
把第1,2两个图中的阴影部分一起并入第3个图,这时第3个图中的阴影小正方形数就是前面三个图中阴影小正方形数的和,记作S3,即
S3=a1+a2+a3=1+3+5=32.
观察排列的图案,归纳并猜想结果:
S2=a1+a2=1+3=22,
S3=a1+a2+a3=1+3+5=32,
S1=a1 =1,
a1+a2+a3+a4=1+3+5+7=42
S4=______________________,
S5=___________________________,
a1+a2+a3+a4+a5=1+3+5+7+9=52
……
Sn=__________________________________.
a1+a2+a3+…+ an =1+3+5+…+(2n-1)=n2
根据某类事物的部分对象具有的某种性质,推出这类事物的所有对象都具有这种性质的推理,叫作归纳推理.
归纳推理
思考:
1.观察下面两列数,通过归纳,给出每个序列中的后续项:
(1)1,2,4,8,16,32,_____,_____;
×2
×2
×2
×2
×2
×2
×2
64
128
(2)20,18,16,14,12,10,_____,_____.
-2
8
6
-2
-2
-2
-2
-2
-2
思考:
2. 平面内2条直线、3条直线、4条直线最多有几个交点?n条呢?
1个
1+2=3个
1+2+3=6个
2条直线
3条直线
4条直线
n条直线最多有1+2+3+…+(n-1)= 个交点
数学史话
数学符号
在古代,要记录、说明、解决一个数学问题,通常要采取刻痕、画图或写字等方式表达.
上图是埃及出土的“莱茵德纸草书”(约公元前1650年)上的问题. 用现在的数学符号来表示,就是:
我国古代在商代创立了甲骨文的10进非位值制记数法. 此后,大约在春秋时期(公元前770年至公元前476年)又创造了一种筹算的10进位制记数法.
点击图片播放视频
数学符号系统化首先归功于法国数学家韦达. 他受古希腊数学家丢番图在著作中采用了一些符号的启发,第一次有意识地系统使用代数字母与符号.
其后,许多数学家对数学符号系统的完善都作出过很多贡献.
随堂演练
1.观察下列数据: 试确定第2022个数是( )
A
2.观察下列各等式:
-2+3=1;
-5-6+7+8=4;
-10-11-12+13+14+15=9;
-17-18-19-20+21+22+23+24=16;
…
根据以上规律可知第11个等式中左起第11个数是( )
A.-130 B.-131 C.-132 D.-133
C
3.下面用棋子摆成的“上”字:
若按照以上规律继续摆下去,则通过观察可以发现:摆第n个“上”字需要用________枚棋子.
(4n+2)
课堂小结
根据某类事物的部分对象具有的某种性质,推出这类事物的所有对象都具有这种性质的推理,叫做归纳推理.
归纳推理
1.从教材习题中选取.
2.完成练习册本课时的习题.
布置作业
数学活动
沪科版 七年级上册
进行新课
数学活动
探索规律
探究1:一个两位数,个位上的数字为a,十位上的数字为b.
(1)这两位数可以用代数式表示为_________;
(2)如果a+b能被3整除,那么这个两位数能被3整除吗?
10b+a
(2)如果a+b能被3整除,那么这个两位数能被3整除吗?
解:(10b+a)-(a+b)
=10b+a-a-b
=9b
因为9b能被3整除,a+b能被3整除,
所以9b+(a+b)=10b+a能被3整除,
即这个两位数能被3整除.
去括号
通过分析计算,你发现了什么规律?
如果一个两位数个位上的数字与十位上的数字之和能被3整除,那么这个两位数能被3整除.
探究2:任意写一个三位数,比如 419. 然后把这个三位数重写一次与它并排构成一个六位数,如419419. 对于这个六位数,先用7去除,把得到的商用11去除,对第二次得到的商再用13去除. 这时,你得到怎样的结果?
419419÷7=59917
59917÷11=5447
5447÷13= 419
再写几个三位数,按上述步骤试试,你有什么发现?
例如:
①三位数273,构成的六位数为273273.
273273÷7=39039
39039÷11=3549
3549÷13=273
②三位数648,构成的六位数为648648.
648648÷7=92664
92664÷11=8424
8424÷13=648
你能说明其中的道理吗?
最后得到的数与原三位数相等
对于任意一个三位数,个位上的数字为a,十位上的数字为b,百位上的数字为c.
(1)这个三位数可以用代数式表示为____________.
(2)把这个三位数重写一次与它并排构成一个六位数,则这个六位数可以用代数式表示为__________________________________.
100c+10b+a
100000c+10000b+1000a+100c+10b+a
100000c+10000b+1000a+100c+10b+a
=100100c+10010b+1001a
=1001(100c+10b+a)
原三位数
7×11×13
即这个六位数,先用7去除,把得到的商用11去除,对第二次得到的商再用13去除,最后的结果等于原三位数.
数学拓展
归纳推理
用一些相同的小正方形,排成如下的一些大正方形图案,如图:
1.把每个图中一边上的小正方形个数和有阴影的小正方形的个数填入表中:
图号(n) 1 2 3 4 5 … k …
一边上小正方形个数(n) 1 2 3 … …
阴影小正方形个数(an) 1 3 5 … …
4
5
7
9
k
2k-1
2. 第1个图中小正方形只有1个,且有阴影,记作S1=1.把第1个图并入第2个图,这时第2个图中阴影小正方形数就是前面两个图中阴影小正方形数的和:a1+a2=1+3=4.我们把这个和a1+a2记作S2,即
S2=a1+a2=1+3=22.
把第1,2两个图中的阴影部分一起并入第3个图,这时第3个图中的阴影小正方形数就是前面三个图中阴影小正方形数的和,记作S3,即
S3=a1+a2+a3=1+3+5=32.
观察排列的图案,归纳并猜想结果:
S2=a1+a2=1+3=22,
S3=a1+a2+a3=1+3+5=32,
S1=a1 =1,
a1+a2+a3+a4=1+3+5+7=42
S4=______________________,
S5=___________________________,
a1+a2+a3+a4+a5=1+3+5+7+9=52
……
Sn=__________________________________.
a1+a2+a3+…+ an =1+3+5+…+(2n-1)=n2
根据某类事物的部分对象具有的某种性质,推出这类事物的所有对象都具有这种性质的推理,叫作归纳推理.
归纳推理
思考:
1.观察下面两列数,通过归纳,给出每个序列中的后续项:
(1)1,2,4,8,16,32,_____,_____;
×2
×2
×2
×2
×2
×2
×2
64
128
(2)20,18,16,14,12,10,_____,_____.
-2
8
6
-2
-2
-2
-2
-2
-2
思考:
2. 平面内2条直线、3条直线、4条直线最多有几个交点?n条呢?
1个
1+2=3个
1+2+3=6个
2条直线
3条直线
4条直线
n条直线最多有1+2+3+…+(n-1)= 个交点
数学史话
数学符号
在古代,要记录、说明、解决一个数学问题,通常要采取刻痕、画图或写字等方式表达.
上图是埃及出土的“莱茵德纸草书”(约公元前1650年)上的问题. 用现在的数学符号来表示,就是:
我国古代在商代创立了甲骨文的10进非位值制记数法. 此后,大约在春秋时期(公元前770年至公元前476年)又创造了一种筹算的10进位制记数法.
点击图片播放视频
数学符号系统化首先归功于法国数学家韦达. 他受古希腊数学家丢番图在著作中采用了一些符号的启发,第一次有意识地系统使用代数字母与符号.
其后,许多数学家对数学符号系统的完善都作出过很多贡献.
随堂演练
1.观察下列数据: 试确定第2022个数是( )
A
2.观察下列各等式:
-2+3=1;
-5-6+7+8=4;
-10-11-12+13+14+15=9;
-17-18-19-20+21+22+23+24=16;
…
根据以上规律可知第11个等式中左起第11个数是( )
A.-130 B.-131 C.-132 D.-133
C
3.下面用棋子摆成的“上”字:
若按照以上规律继续摆下去,则通过观察可以发现:摆第n个“上”字需要用________枚棋子.
(4n+2)
课堂小结
根据某类事物的部分对象具有的某种性质,推出这类事物的所有对象都具有这种性质的推理,叫做归纳推理.
归纳推理
1.从教材习题中选取.
2.完成练习册本课时的习题.
布置作业
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
