数学七年级上绝对值课件
图片预览








文档简介
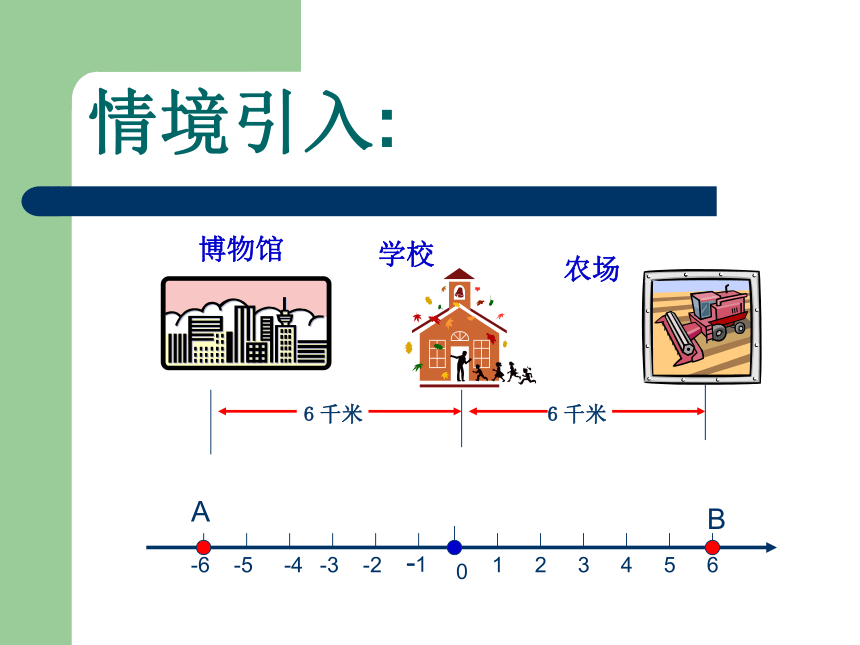
课件22张PPT。绝 对 值新课标人教版七年级数学寻找回忆什么叫做相反数? 你能找出互为相反数的两个数在数轴上表示的点的共同特点吗? 情境引入:情境引入:问:像-5、4的绝对值应该如何记呢? 一个数a的绝对值就是数轴上表示这个数的点与原点之间的距离。一个数的绝对值应该怎么样去记呢?一个数a的绝对值用 |a| 表示。
-5的绝对值应该记作│-5︱=?
4的绝对值应该记作│4︱=?
0的绝对值应该如何记呢?
一般地,数轴上表示数a的点与原点的距离叫做数a的绝对值。
想一想 互为相反数的两个数的绝对值有什么关系?想一想 这里的数a可以表示什么样的数?这里的数a可以是正数,负数和0 一对相反数虽然分别在原点两边,但它们到原点的距离是相等的。
1.表示+7的点与原点的距离是 ,即+7的绝值是 ,记作 ;
2.表示2.8的点与原点的距离是 ,即2.8的绝对值是 ,记作 ;
3.表示0的点与原点的距离是 ,即0的绝对值是 ,记作 ;
4. 表示-5的点与原点的距离是 ,即-5的绝对值是 ,记作 ;练习:议一议: 一个数的绝对值与这个数有什么关系?例如:|3|=3,|+7|=7 …………一个正数的绝对值是它本身例如:|-3|=3,|-2.3|=2.3 ………… 一个负数的绝对值是它的相反数0的绝对值是0。即 |0|=0而 原点到原点的距离是0绝对值的性质:绝对值的性质:
(1)正数的绝对值是它的本身;
(2)0的绝对值是0;
(3)负数的绝对值是它的相反数。做一做写出下列各数的绝对值:
解: ⑴计算:│-32︱= ;│+0.25│= ;
│0│= .
⑵用>、<、=号填空:
│-0.05│ 0; │-3│ 0;
│0.8│ │-0.8│
⑶判断(对的打“√”,错的打“×”):
(1)一个有理数的绝对值一定是正数。 ( )
(2)-1.4<0,则│-1.4│<0。 ( )
(3) │-32︱的相反数是32 ( )
练习:
1、符号是“+”号,绝对值是6的数是 ;符号是“-”号,绝对值是6的数是 ;绝对值等于6的数有几个?
2、绝对值是0的数是 。
3、在数轴上与原点的距离等于6的点有哪些?
练习:判断:
(1)一个数的绝对值是 2?,则这数是2 。 (2)|5|=|-5|。 (3)|-0.3|=|0.3|。 (4)|3|>0。 (5)|-1.4|>0。
(6)有理数的绝对值一定是正数。
(7)若a=b,则|a|=|b|。 (8)若|a|=|b|,则a=b。
(9)若|a|=-a,则a必为负数。 (10)互为相反数的两个数的绝对值相等。想一想1) 绝对值是7的数有几个?各是什么?有
没有绝对值是-2的数?答:绝对值是7的数有两个,各是7与-7。 没有绝对值是-2的数。 绝对值是0的数有几个?各是什么?
答:绝对值是0的数有一个,就是0。
3)绝对值小于3的整数一共有多少个?答:绝对值小于3的整数一共有5个,它们分别是-2,-1,0,1,2。思考:足球比赛中对所用的足球有严格的规定,下面是5个足球的质量检测结果(用正数表示超过规定质量的克数,用负数表示不足规定质量的克数)-20 +10 +12 -8 -11请指出哪个足球的质量好一些,并用绝对值的知识加以说明。
答:记为-8的足球质量好一些。
因为│-20│=20,│+10│=10,│+12│=12,
│-8│=8,│-11│=11;所以│-8│ < │+10│ < │-11│ < │+12│ < │-20│也就是说记为-8的足球与规定的质量相差比较小,因此其质量比较好。 2、已知有理数a在数轴上对应的点如图所示:则|a| =________ 4、如果a 的相反数是-0.74,那么|a| =______ 3. 如果一个数的绝对值等于3.25 ,则这个数是___ 5. 如果|x-1|=2,则x=______.课堂升华a0本节课你掌握了以下知识吗?绝对值的定义是什么?
绝对值的性质是什么?作业:习题 1.2
4,7 ,10。
(1)求绝对值不大于2的整数; (2)已知x是整数,且2.5<|x|<7,求x. 思考1.下列说法正确的是( )
A.一个数的绝对值一定是正数
B.一个数的绝对值一定是负数
C.一个数的绝对值一定不是负数
D.一个数的绝对值的相反数一定是负数
2.如果一个数的绝对值等于它的相反数,那么这个数( )
A.必为正数 B.必为负数
C.一定不是正数 D.一定不是负数
3.下列语句正确的个数有( )
①若a=b,则|a|=|b|;②若a= –b,则|a|=|b|;
③若|a|=|b|,则a=b;④若|a|=b,则a=b;
⑤若|a|= –b,则a= –b;⑥若|a|=b,则a=±b。
A.2个 B.3个 C.4个 D.5个 4.绝对值等于4的数是( )
A.4 B.–4 C.±4 D.以上均不对
5.计算:|–(+3.6)|+|–(–1.2)|–|–[+(–4)]|
七、课后思考
已知|x–2|+|y–3|+|z–4|=0,求x+y–z的值。
-5的绝对值应该记作│-5︱=?
4的绝对值应该记作│4︱=?
0的绝对值应该如何记呢?
一般地,数轴上表示数a的点与原点的距离叫做数a的绝对值。
想一想 互为相反数的两个数的绝对值有什么关系?想一想 这里的数a可以表示什么样的数?这里的数a可以是正数,负数和0 一对相反数虽然分别在原点两边,但它们到原点的距离是相等的。
1.表示+7的点与原点的距离是 ,即+7的绝值是 ,记作 ;
2.表示2.8的点与原点的距离是 ,即2.8的绝对值是 ,记作 ;
3.表示0的点与原点的距离是 ,即0的绝对值是 ,记作 ;
4. 表示-5的点与原点的距离是 ,即-5的绝对值是 ,记作 ;练习:议一议: 一个数的绝对值与这个数有什么关系?例如:|3|=3,|+7|=7 …………一个正数的绝对值是它本身例如:|-3|=3,|-2.3|=2.3 ………… 一个负数的绝对值是它的相反数0的绝对值是0。即 |0|=0而 原点到原点的距离是0绝对值的性质:绝对值的性质:
(1)正数的绝对值是它的本身;
(2)0的绝对值是0;
(3)负数的绝对值是它的相反数。做一做写出下列各数的绝对值:
解: ⑴计算:│-32︱= ;│+0.25│= ;
│0│= .
⑵用>、<、=号填空:
│-0.05│ 0; │-3│ 0;
│0.8│ │-0.8│
⑶判断(对的打“√”,错的打“×”):
(1)一个有理数的绝对值一定是正数。 ( )
(2)-1.4<0,则│-1.4│<0。 ( )
(3) │-32︱的相反数是32 ( )
练习:
1、符号是“+”号,绝对值是6的数是 ;符号是“-”号,绝对值是6的数是 ;绝对值等于6的数有几个?
2、绝对值是0的数是 。
3、在数轴上与原点的距离等于6的点有哪些?
练习:判断:
(1)一个数的绝对值是 2?,则这数是2 。 (2)|5|=|-5|。 (3)|-0.3|=|0.3|。 (4)|3|>0。 (5)|-1.4|>0。
(6)有理数的绝对值一定是正数。
(7)若a=b,则|a|=|b|。 (8)若|a|=|b|,则a=b。
(9)若|a|=-a,则a必为负数。 (10)互为相反数的两个数的绝对值相等。想一想1) 绝对值是7的数有几个?各是什么?有
没有绝对值是-2的数?答:绝对值是7的数有两个,各是7与-7。 没有绝对值是-2的数。 绝对值是0的数有几个?各是什么?
答:绝对值是0的数有一个,就是0。
3)绝对值小于3的整数一共有多少个?答:绝对值小于3的整数一共有5个,它们分别是-2,-1,0,1,2。思考:足球比赛中对所用的足球有严格的规定,下面是5个足球的质量检测结果(用正数表示超过规定质量的克数,用负数表示不足规定质量的克数)-20 +10 +12 -8 -11请指出哪个足球的质量好一些,并用绝对值的知识加以说明。
答:记为-8的足球质量好一些。
因为│-20│=20,│+10│=10,│+12│=12,
│-8│=8,│-11│=11;所以│-8│ < │+10│ < │-11│ < │+12│ < │-20│也就是说记为-8的足球与规定的质量相差比较小,因此其质量比较好。 2、已知有理数a在数轴上对应的点如图所示:则|a| =________ 4、如果a 的相反数是-0.74,那么|a| =______ 3. 如果一个数的绝对值等于3.25 ,则这个数是___ 5. 如果|x-1|=2,则x=______.课堂升华a0本节课你掌握了以下知识吗?绝对值的定义是什么?
绝对值的性质是什么?作业:习题 1.2
4,7 ,10。
(1)求绝对值不大于2的整数; (2)已知x是整数,且2.5<|x|<7,求x. 思考1.下列说法正确的是( )
A.一个数的绝对值一定是正数
B.一个数的绝对值一定是负数
C.一个数的绝对值一定不是负数
D.一个数的绝对值的相反数一定是负数
2.如果一个数的绝对值等于它的相反数,那么这个数( )
A.必为正数 B.必为负数
C.一定不是正数 D.一定不是负数
3.下列语句正确的个数有( )
①若a=b,则|a|=|b|;②若a= –b,则|a|=|b|;
③若|a|=|b|,则a=b;④若|a|=b,则a=b;
⑤若|a|= –b,则a= –b;⑥若|a|=b,则a=±b。
A.2个 B.3个 C.4个 D.5个 4.绝对值等于4的数是( )
A.4 B.–4 C.±4 D.以上均不对
5.计算:|–(+3.6)|+|–(–1.2)|–|–[+(–4)]|
七、课后思考
已知|x–2|+|y–3|+|z–4|=0,求x+y–z的值。
