人教版八年级数学上名师点拨精练第11章三角形11.1.1 三角形的边 (含解析)
文档属性
| 名称 | 人教版八年级数学上名师点拨精练第11章三角形11.1.1 三角形的边 (含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-17 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
人教版八年级数学上名师点拨精练
第11章 三角形
11.1.1 三角形的边
学习目标
1.认识三角形的边、内角、顶点,能用几何语言表示三角形;
2.掌握三角形的三边关系定理,能利用定理及其推论进行简单的证明;
3.了解三角形分类的原则和结论.
老师告诉你
判断三条线段能否构成三角形,只需看较短的两条线段的和是否大于第三条线段,因为只要较短的两条线段的和大于第三条线段,则任意两条线段的和都大于第三条线段,所以用此方法能很快地判断出三条线段能否构成三角形。
知识点拨
知识点1.三角形及有关概念
1.定义 由不在同一条直线上的三条线段首尾顺次相接所组成的图形叫做三角形.
构成三角形的三个基本条件:①不在同一条直线上;②三条线段;③首尾顺次相接.
2.(1)构成三角形的基本元素:
①三角形的边:即组成三角形的线段;
②三角形的角:即相邻两边所组成的角叫做三角形的内角,简称三角形的角;
③三角形的顶点:即相邻两边的公共端点.
3 .三角形的表示:三角形用符号“△”表示,顶点为A、B、C的三角形记作“△ABC”,读作“三角形ABC”,注意单独的△没有意义;△ABC的三边可以用大写字母AB、BC、AC来表示,也可以用小写字母a、b、c来表示,边BC用a表示,边AC、AB分别用b、c表示.
【新知导学】
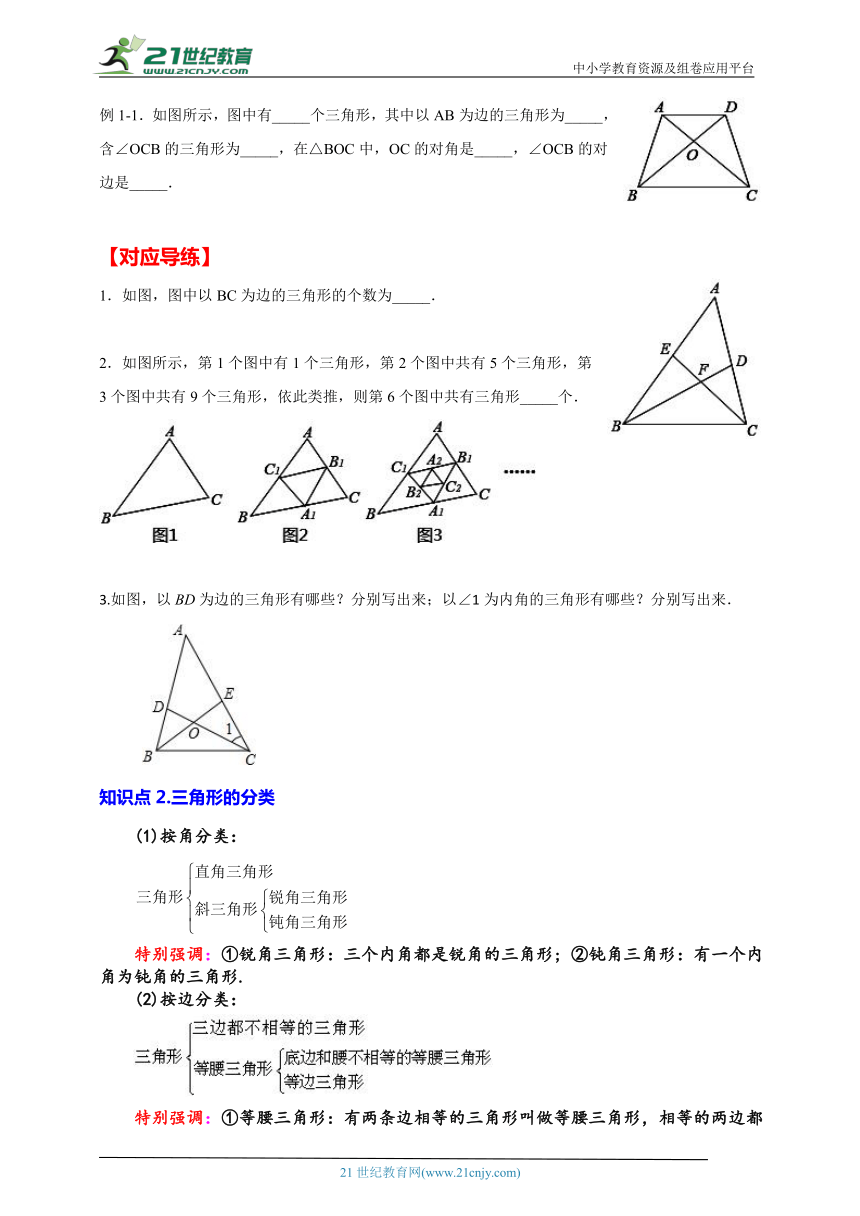
例1-1.如图所示,图中有_____个三角形,其中以AB为边的三角形为_____,含∠OCB的三角形为_____,在△BOC中,OC的对角是_____,∠OCB的对边是_____.
【对应导练】
1.如图,图中以BC为边的三角形的个数为_____.
2.如图所示,第1个图中有1个三角形,第2个图中共有5个三角形,第3个图中共有9个三角形,依此类推,则第6个图中共有三角形_____个.
3.如图,以BD为边的三角形有哪些?分别写出来;以∠1为内角的三角形有哪些?分别写出来.
知识点2.三角形的分类
(1)按角分类:
特别强调:①锐角三角形:三个内角都是锐角的三角形; ②钝角三角形:有一个内角为钝角的三角形.
(2)按边分类:
特别强调:①等腰三角形:有两条边相等的三角形叫做等腰三角形,相等的两边都叫做腰,另外一边叫做底边,两腰的夹角叫顶角,腰与底边夹角叫做底角; ②等边三角形:三边都相等的三角形.
【新知导学】
例2-1.下列关于三角形的分类,正确的是( )
A. B.
C. D.
【对应导练】
1.三角形按边分类可以用集合来表示,如图所示,图中小椭圆圈里的A表示( )
A. 直角三角形 B. 锐角三角形
C. 钝角三角形 D. 等边三角形
2 .关于三角形的分类,有如图所示的甲、乙两种分法,则( )
A.甲、乙两种分法均正确 B.甲、乙两种分法均错误
C.甲的分法错误,乙的分法正确 D.甲的分法正确,乙的分法错误
知识点3 三角形三边关系
定理:三角形任意两边的和大于第三边(理论依据:两点之间线段最短).
推论:三角形任意两边的差小于第三边.
三边关系的应用:
判断三条线段能否组成三角形,若两条较短的线段长之和大于最长线段的长,则这三条线段可以组成三角形;反之,则不能组成三角形.当已知三角形两边长,可求第三边长的取值范围.
(2)证明线段之间的不等关系.
【新知导学】
例3-1.已知三角形两边的长分别为2cm、7cm,第三边长为整数,则第三边的长可以为( )
A. 4cm B. 5cm C. 8cm D. 9cm
【对应导练】
1.在下列长度的四条线段中,能与长6cm,8cm的两条线段围成一个三角形的是( )
A. 1cm B. 2cm C. 13cm D. 14cm
2.等腰三角形的周长为20cm,一边为8cm,则腰长为( )
A. 4cm B. 8cm C. 4cm或8cm D. 6cm或8cm
3.已知a,b,c是△ABC的三边长,满足|a-7|+(b-2)2=0,c为奇数,则△ABC的周长为 _____.
4.等腰三角形的周长为20cm,一边长为6cm,则底边长为_____cm.
5.已知a,b,c是△ABC的三边长,b,c满足(b-2)2+|c-3|=0,且a为方程|x-4|=2的解,求△ABC的周长.
二、题型训练
1.三角形的分类在判断三角形形状中的应用
1.已知a,b,c是的三边长,b,c满足,且a为方程的解,求的周长,并判断三角形的形状。
2.已知a,b,c是的三边长,,,设的周长是x.
(1)求c与x的取值范围;
(2)若x是小于18的偶数,试判断的形状.
2.三角形三边关系在拼图中的应用
3.定义:三边长和面积都是整数的三角形称为“整数三角形”.
数学学习小组的同学从32根等长的火柴棒(每根长度记为1个单位)中取出若干根,首尾依次相接组成三角形,进行探究活动.
小亮用12根火柴棒,摆成如图所示的“整数三角形”;
小颖分别用24根和30根火柴棒摆出直角“整数三角形”;
小辉受到小亮、小颖的启发,分别摆出三个不同的等腰“整数三角形”.
(1)请你画出小颖和小辉摆出的“整数三角形”的示意图;
(2)你能否也从中取出若干根摆出等边“整数三角形”,如果能,请画出示意图;如果不能,请说明理由.
3.等腰三角形的三边长分别为,,7,求等腰三角形的周长.
4.已知a,b,c为△ABC的三边长,且b,c满足,a为方程的解,求△ABC的周长,并判断△ABC的形状.
3.三角形三边关系在证明线段大小关系中的应用
5.如图,点P是△ABC内部的一点,连接PB,PC.
(1)度量线段AB,AC,PB,PC的长度,根据度量结果比较与的大小;
(2)改变点P的位置,上述结论还成立吗?
(3)你能说明上述结论为什么正确吗?
三、牛刀小试
一、单选题(每小题3分,共24分)
1.下面是一位同学用三根木棒拼成的图形,其中是三角形的是( )
A. B.
C. D.
2.下列说法正确的有( )
①等腰三角形是等边三角形;
②三角形按边分类可分为等腰三角形、等边三角形和不等边三角形;
③等腰三角形至少有两边相等;
④三角形按角分类应分为锐角三角形、直角三角形和钝角三角形.
A.①② B.①③④ C.③④ D.①②④
3.以下列各组线段为边不能组成三角形的是( )
A.3,4,4 B.2,6,8 C.2,5,4 D.6,8,10
4.设一个三角形的三边长分别为5、m、8,则m的取值范围是( )
A. B. C. D.
5.已知某等腰三角形三边长分别为5,a,11,则a的值为( )
A.5 B.5.5 C.11 D.5或11
6.设M表示直角三角形,N表示等腰三角形,P表示等边三角形,Q表示等腰直角三角形.下列四个选项中,能正确表示它们之间的关系的是( )
A. B.
C. D.
7.如图是一组按照某种规律摆放成的图形,则第5个图形中三角形的个数是( )
A.8 B.9 C.16 D.17
8.已知三角形的三边长分别为a,b,c,化简得( )
A. B. C. D.0
二、填空题(每小题4分,共20分)
9.已知等腰三角形的两边长分别为和,则它的周长是______.
10.若等腰三角形的两边长分别为6cm和8cm,则它的周长是________.
11.已知等腰三角形的周长为20,其中一边的长为6,则底边的长为_________.
12.已知a,b,c是的三条边长,则_________.
.
13.5条线段的长度分别为l cm,2 cm,3 cm,4 cm,5 cm,以其中的三条线段组成三角形,则可组成不同的三角形的个数是__________.
三、解答题(共7小题,共56分)
14.(8分)两根木棒的长分别是5cm和7cm.要选择第三根木棒,将它们首尾相接钉成一个三角形.若第三根木棒的长为偶数,则第三根木棒长的取值情况有几种
15.(8分)已知等腰三角形的两边长分别为4和10,求这个等腰三角形的周长.
16.(8分)如图,在三角形ABC中,,,D是BC的中点,E点在边AB上.
(1)若三角形BDE的周长与四边形ACDE的周长相等,求线段AE的长.
(2)若三角形ABC的周长被DE分成的两部分的差是2 cm,求线段AE的长.
17.(8分)已知a,b,c是的三边长,,,设的周长是x.
(1)求c与x的取值范围;
(2)若x是小于18的偶数,试判断的形状.
18.(8分)按要求完成下列各小题.
(1)在中,,,的长为偶数,求的周长;
(2)已知的三边长分别为3,5,a,化简.
19.(8分)阅读材料:若求的值.
解:∵
根据你的观察,探究下面的问题:
(1). ,则____________________
(2).已知求的值
(3).已知的三边长都是正整数,且满足求的周长
20.(8分)如图所示,已知是三角形内一点,连接、,试探究与的大小关系.
人教版八年级数学上名师点拨精练
第11章 三角形
11.1.1 三角形的边(解析版)
学习目标
1.认识三角形的边、内角、顶点,能用几何语言表示三角形;
2.掌握三角形的三边关系定理,能利用定理及其推论进行简单的证明;
3.了解三角形分类的原则和结论.
老师告诉你
判断三条线段能否构成三角形,只需看较短的两条线段的和是否大于第三条线段,因为只要较短的两条线段的和大于第三条线段,则任意两条线段的和都大于第三条线段,所以用此方法能很快地判断出三条线段能否构成三角形。
知识点拨
知识点1.三角形及有关概念
1.定义 由不在同一条直线上的三条线段首尾顺次相接所组成的图形叫做三角形.
构成三角形的三个基本条件:①不在同一条直线上;②三条线段;③首尾顺次相接.
2.(1)构成三角形的基本元素:
①三角形的边:即组成三角形的线段;
②三角形的角:即相邻两边所组成的角叫做三角形的内角,简称三角形的角;
③三角形的顶点:即相邻两边的公共端点.
3 .三角形的表示:三角形用符号“△”表示,顶点为A、B、C的三角形记作“△ABC”,读作“三角形ABC”,注意单独的△没有意义;△ABC的三边可以用大写字母AB、BC、AC来表示,也可以用小写字母a、b、c来表示,边BC用a表示,边AC、AB分别用b、c表示.
【新知导学】
例1-1.如图所示,图中有_____个三角形,其中以AB为边的三角形为_____,含∠OCB的三角形为_____,在△BOC中,OC的对角是_____,∠OCB的对边是_____.
【答案】(1)8;(2)△ABC,△ABD,△ABO;(3)△OCB,△ACB;(4)∠OBC;(5)OB;
【解析】根据三角形的边和角有关概念解答.
解:,图中有8个三角形,其中以AB为边的三角形为△ABC,△ABD,△ABO,含∠OCB的三角形为△OCB,△ACB,在△BOC中,OC的对角是∠OBC,∠OCB的对边是OB,
故答案为:8;△ABC,△ABD,△ABO;△OCB,△ACB;∠OBC;OB.
【对应导练】
1.如图,图中以BC为边的三角形的个数为_____.
【答案】4
【解析】根据三角形的定义即可得到结论.
解:∵以BC为公共边的三角形有△BCD,△BCE,△BCF,△ABC,
∴以BC为公共边的三角形的个数是4个.
故答案为:4.
2.如图所示,第1个图中有1个三角形,第2个图中共有5个三角形,第3个图中共有9个三角形,依此类推,则第6个图中共有三角形_____个.
【答案】21
【解析】根据前边的具体数据,再结合图形,不难发现:后边的总比前边多4,即第n个图形中,三角形的个数是1+4(n-1)=4n-3.
所以当n=6时,原式=21.注意规律:后面的图形比前面的多4个.
解:第n个图形中,三角形的个数是1+4(n-1)=4n-3.所以当n=6时,原式=21,
故答案为:21.
3.如图,以BD为边的三角形有哪些?分别写出来;以∠1为内角的三角形有哪些?分别写出来.
【分析】先根据BD边找三角形,再根据∠1找三角形.
解:以BD为边的三角形有:△BDC,△BDO,
以∠1为内角的三角形有:△EOC,△ACD.
【点拨】本题考查了三角形的内角和边的概念,学会分类的方法找三角形是本题的解题关键.
知识点2.三角形的分类
(1)按角分类:
特别强调:①锐角三角形:三个内角都是锐角的三角形; ②钝角三角形:有一个内角为钝角的三角形.
(2)按边分类:
特别强调:①等腰三角形:有两条边相等的三角形叫做等腰三角形,相等的两边都叫做腰,另外一边叫做底边,两腰的夹角叫顶角,腰与底边夹角叫做底角; ②等边三角形:三边都相等的三角形.
【新知导学】
例2-1.下列关于三角形的分类,正确的是( )
A. B.
C. D.
【答案】B
【解析】根据三角形的分类可直接选出答案.
解:A、等腰直角三角形应该是直角三角形,不符合题意;
B、该选项中的三角形的分类正确,符合题意;
C、等腰三角形包括等边三角形,不符合题意;
D、等腰三角形包括等边三角形,不符合题意;
故选:B.
【对应导练】
1.三角形按边分类可以用集合来表示,如图所示,图中小椭圆圈里的A表示( )
A. 直角三角形 B. 锐角三角形
C. 钝角三角形 D. 等边三角形
【答案】D
【解析】根据三角形的分类可直接得到答案.
解:三角形根据边分类 ,
∴图中小椭圆圈里的A表示等边三角形.
故选:D.
2 .关于三角形的分类,有如图所示的甲、乙两种分法,则( )
A.甲、乙两种分法均正确 B.甲、乙两种分法均错误
C.甲的分法错误,乙的分法正确 D.甲的分法正确,乙的分法错误
【答案】D
【分析】三角形的分类:按边分有普通三角形(三条边都不相等),等腰三角(腰与底不等的等腰三角形、腰与底相等的等腰三角形即等边三角形);按角分有直角三角形、锐角三角形、钝角三角形等,其中锐角三角形和钝角三角形统称斜三角形.据此判断即可.
【详解】解:甲分法正确,乙正确的分类应该为:
故选:D.
【点评】本题考查三角形的分类,解答的关键是熟知三角形的分类标准,易忽略等腰三角形包含等边三角形.
知识点3 三角形三边关系
定理:三角形任意两边的和大于第三边(理论依据:两点之间线段最短).
推论:三角形任意两边的差小于第三边.
三边关系的应用:
判断三条线段能否组成三角形,若两条较短的线段长之和大于最长线段的长,则这三条线段可以组成三角形;反之,则不能组成三角形.当已知三角形两边长,可求第三边长的取值范围.
(2)证明线段之间的不等关系.
【新知导学】
例3-1.已知三角形两边的长分别为2cm、7cm,第三边长为整数,则第三边的长可以为( )
A. 4cm B. 5cm C. 8cm D. 9cm
【答案】C
【解析】根据三角形的三边关系得出第三边的范围,进而得到答案.
解:设第三边的长为x cm,
则7-2<x<7+2,即5<x<9,
∵第三边的长为整数,
∴第三边的长可以为8cm.
故选:C.
【对应导练】
1.在下列长度的四条线段中,能与长6cm,8cm的两条线段围成一个三角形的是( )
A. 1cm B. 2cm C. 13cm D. 14cm
【答案】C
【解析】首先设第三条线段长为x cm,再利用三角形的三边关系可得x的范围,然后可得答案.
解:设第三条线段长为x cm,由题意得:
8-6<x<8+6,
解得:2<x<14,
只有13cm适合,
故选:C.
2.等腰三角形的周长为20cm,一边为8cm,则腰长为( )
A. 4cm B. 8cm C. 4cm或8cm D. 6cm或8cm
【答案】D
【解析】分8cm是等腰三角形的腰长与底边长两种情况进行讨论.
解:∵等腰三角形的周长为20cm,
∴当8cm是腰长时,底边=20-8-8=4cm;
∴当8cm是底边长时,腰长==6cm,
∴腰长为8cm或6cm,
故选:D.
3.已知a,b,c是△ABC的三边长,满足|a-7|+(b-2)2=0,c为奇数,则△ABC的周长为 _____.
【答案】16
【解析】根据在三角形中任意两边之和>第三边,任意两边之差<第三边;可求第三边长的范围,再根据奇数的定义得出答案.
解:∵|a-7|+(b-2)2=0,
∴a-7=0,b-2=0,
解得:a=7,b=2,
由三角形三边关系定理得:7-2<c<7+2,即5<c<9,
又∵c为奇数,
∴c=7,
∴△ABC的周长为7+2+7=16.
故答案为:16.
4.等腰三角形的周长为20cm,一边长为6cm,则底边长为_____cm.
【答案】6或8
【解析】分6cm是底边与腰长两种情况讨论求解.
解:①6cm是底边时,腰长=(20-6)=7cm,
此时三角形的三边分别为7cm、7cm、6cm,
能组成三角形,
②6cm是腰长时,底边=20-6×2=8cm,
此时三角形的三边分别为6cm、6cm、8cm,
能组成三角形,
综上所述,底边长为6或8cm.
故答案为:6或8.
5.已知a,b,c是△ABC的三边长,b,c满足(b-2)2+|c-3|=0,且a为方程|x-4|=2的解,求△ABC的周长.
【解析】利用绝对值的性质以及偶次方的性质得出b,c的值,进而利用三角形三边关系得出a的值,进而可得出其周长.
解:∵(b-2)2+|c-3|=0,
∴b-2=0,c-3=0,
解得:b=2,c=3,
∵a为方程|x-4|=2的解,
∴x-4=±2,
解得:x=6或2.
∵a、b、c为△ABC的三边长,b+c<6,
∴x=6不合题意舍去,
∴a=2,
∴△ABC的周长=a+b+c=2+2+3=7.
二、题型训练
1.三角形的分类在判断三角形形状中的应用
1.已知a,b,c是的三边长,b,c满足,且a为方程的解,求的周长,并判断三角形的形状。
答案:7,三角形是等腰三角形
解析:因为,所以,,解得,.因为a为方程的解,所以,解得或2.因为a,b,c为的三边长,所以,所以,所以的周长为.故答案为7.
a=b=2,所以三角形是等腰三角形
2.已知a,b,c是的三边长,,,设的周长是x.
(1)求c与x的取值范围;
(2)若x是小于18的偶数,试判断的形状.
答案:(1);
(2)是等腰三角形
解析:(1)因为,,所以.
故周长x的取值范围是.
(2)因为x是小于18的偶数,
所以或.
当时,;
当时,.
当时,,为等腰三角形;
当时,,为等腰三角形.
综上,是等腰三角形.
2.三角形三边关系在拼图中的应用
3.定义:三边长和面积都是整数的三角形称为“整数三角形”.
数学学习小组的同学从32根等长的火柴棒(每根长度记为1个单位)中取出若干根,首尾依次相接组成三角形,进行探究活动.
小亮用12根火柴棒,摆成如图所示的“整数三角形”;
小颖分别用24根和30根火柴棒摆出直角“整数三角形”;
小辉受到小亮、小颖的启发,分别摆出三个不同的等腰“整数三角形”.
(1)请你画出小颖和小辉摆出的“整数三角形”的示意图;
(2)你能否也从中取出若干根摆出等边“整数三角形”,如果能,请画出示意图;如果不能,请说明理由.
(1)答案:见解析
解析:小颖摆出如图1所示的“整数三角形”:
小辉摆出如图2所示三个不同的等腰“整数三角形”:
(2)答案:不能摆出等边“整数三角形”
解析:不能摆出等边“整数三角形”.理由如下:
设等边三角形的边长为a,则等边三角形面积为.
因为,若边长a为整数,那么面积一定非整数.
所以不存在等边“整数三角形”.
3.等腰三角形的三边长分别为,,7,求等腰三角形的周长.
答案:三角形的周长为19.5或23
解析:①当是底边时,则腰长为:,7,
,
,
,
等腰三角形的周长;
②当是底边时,则腰长为:,7,
,
,
,
等腰三角形的周长;
③当7是底边时,则腰长为:,,
,
,
,,
,
不能构成三角形.
则三角形的周长为19.5或23.
4.已知a,b,c为△ABC的三边长,且b,c满足,a为方程的解,求△ABC的周长,并判断△ABC的形状.
答案:因为,
所以,解得.
因为a为方程的解,所以或1.
当时,,不能构成三角形,
所以不符合题意;
当时,,能构成三角形,
此时,△ABC的周长为.
综上,△ABC的周长为17.
因为,所以△ABC是等腰三角形.
3.三角形三边关系在证明线段大小关系中的应用
5.如图,点P是△ABC内部的一点,连接PB,PC.
(1)度量线段AB,AC,PB,PC的长度,根据度量结果比较与的大小;
(2)改变点P的位置,上述结论还成立吗?
(3)你能说明上述结论为什么正确吗?
答案:(1)经度量, cm, cm, cm, cm,
所以.
(2)成立.
(3)延长BP交AC于点D.
在△ABD中,,①
在△PDC中,,②
,得,
所以.
三、牛刀小试
一、单选题(每小题3分,共24分)
1.下面是一位同学用三根木棒拼成的图形,其中是三角形的是( )
A. B.
C. D.
答案:D
解析:由不在同一条直线上的三条线段首尾顺次相接所组成的图形叫做三角形,由此可知A,B,C不是三角形,D是三角形.
故选D
2.下列说法正确的有( )
①等腰三角形是等边三角形;
②三角形按边分类可分为等腰三角形、等边三角形和不等边三角形;
③等腰三角形至少有两边相等;
④三角形按角分类应分为锐角三角形、直角三角形和钝角三角形.
A.①② B.①③④ C.③④ D.①②④
答案:C
解析:①有两条边相等的三角形是等腰三角形,三条边都相等的三角形是等边三角形,等腰三角形不一定是等边三角形,①错误;
②三角形按边分类可分为三边都不相等的三角形和等腰三角形,其中等腰三角形又可分为底边和腰不相等的三角形和等边三角形,②错误;③有两条边相等的三角形是等腰三角形,③正确;④三角形按角分类可以分为锐角三角形、直角三角形、钝角三角形,④正确.故选C.
3.以下列各组线段为边不能组成三角形的是( )
A.3,4,4 B.2,6,8 C.2,5,4 D.6,8,10
答案:B
解析:根据构成三角形条件,两边之和大于第三边,A 3+4>4.能够组成三角形,B 2+6=8,不能组成三角形,C 2+4=6>5,能够组成三角形,D 6+8=14>10,能够组成三角形。
故选B
4.设一个三角形的三边长分别为5、m、8,则m的取值范围是( )
A. B. C. D.
答案:A
解析:根据组成三角形的条件,第三边小于两边之和,大于两边之差,所以
故选A
5.已知某等腰三角形三边长分别为5,a,11,则a的值为( )
A.5 B.5.5 C.11 D.5或11
答案:C
解析:根据组成三角形的条件,第三边小于两边之和,大于两边之差,所以6故选C
6.设M表示直角三角形,N表示等腰三角形,P表示等边三角形,Q表示等腰直角三角形.下列四个选项中,能正确表示它们之间的关系的是( )
A. B.
C. D.
答案:C
解析:根据各类三角形的概念可知,C选项可以表示它们之间的关系.故选C.
7.如图是一组按照某种规律摆放成的图形,则第5个图形中三角形的个数是( )
A.8 B.9 C.16 D.17
答案:C
解析:第1个图形中三角形的个数是1;第2个图形中三角形的个数是;第3个图形中三角形的个数是;第4个图形中三角形的个数是.由此可知,从第2个图形开始,后一个图形比前一个图形多4个三角形,因此第5个图形中三角形的个数是.故选C.
8.已知三角形的三边长分别为a,b,c,化简得( )
A. B. C. D.0
答案:A
解析:因为的三边长分别是a,b,c,所以必须满足任意两边之和大于第三边,两边之差小于第三边,则,所以.
故选A.
二、填空题(每小题4分,共20分)
9.已知等腰三角形的两边长分别为和,则它的周长是______.
答案:
解析:(1)当长为的边是等腰三角形的底边时,其三边长分别为:、、,
此时三条线段能围成等腰三角形,其周长为:;
(2)当长为的边为等腰三角形的底边时,其三边长分别为:、、,此时三条线段不能围成三角形;
综上所述,两条边长分别为和的等腰三角形的周长为
故答案为:.
点评:本题考查三角形三边关系,正确掌握三角形三边关系是解题的关键。
10.若等腰三角形的两边长分别为6cm和8cm,则它的周长是________.
答案:或
解析:等腰三角形的两条腰相等
①当腰为6cm时:三角形的周长为:;
②当腰为8cm时:三角形的周长为:;
故答案为:或.
11.已知等腰三角形的周长为20,其中一边的长为6,则底边的长为_________.
答案:6或8
解析:设底边长为x,腰长为y,
则,
①当腰长时,
,
;
三边长分别为6,6,8能构成三角形,符合题意;
故;
②当底边长时,
,
;
三边长分别为7,7,6能构成三角形,符合题意;
故;
综上所述,或;
故答案为:6或8.
12.已知a,b,c是的三条边长,则_________.
答案:2a
解析:a,b,c为的三条边长,,,原式.
13.5条线段的长度分别为l cm,2 cm,3 cm,4 cm,5 cm,以其中的三条线段组成三角形,则可组成不同的三角形的个数是__________.
答案:3
解析:以其中的三条线段为边可组成三角形的有①2 cm,3 cm,4 cm;②2 cm,4 cm,5 cm;③3 cm,4 cm,5 cm,共有3种情况故答案为3.
三、解答题(共7小题,共56分)
14.(8分)两根木棒的长分别是5cm和7cm.要选择第三根木棒,将它们首尾相接钉成一个三角形.若第三根木棒的长为偶数,则第三根木棒长的取值情况有几种
答案:第三根木棒长的取值情况有4种.
解析:设第三根木棒长度为xcm,根据题意得:
,即,
第三根木棒的长为偶数,
x可取4,6,8,10,有4种情况.
答:第三根木棒长的取值情况有4种.
点评:本题考查了三角形三边关系,正确掌握三角形三边关系定理是解题关键。
15.(8分)已知等腰三角形的两边长分别为4和10,求这个等腰三角形的周长.
答案:解:①若腰长为4,则三角形三边长为4,4,10,,不符合三角形的三边关系,故腰长不能为4;
②若腰长为10,则三角形三边长为10,10,4,符合三角形的三边关系,此时三角形的周长为24.
点评:本题考查了三角形三边关系,正确掌握三角形三边关系定理是解题关键。
16.(8分)如图,在三角形ABC中,,,D是BC的中点,E点在边AB上.
(1)若三角形BDE的周长与四边形ACDE的周长相等,求线段AE的长.
(2)若三角形ABC的周长被DE分成的两部分的差是2 cm,求线段AE的长.
答案:(1)
(2)AE的长为1 cm或3 cm
解析:(1)因为,四边形,三角形BDE的周长与四边形ACDE的周长相等,D为BC中点,
所以,,
即.
因为,,
所以,所以.
(2)由三角形ABC的周长被DE分成的两部分的差是2 cm,
可得或,
即或,
故AE的长为1 cm或3 cm.
点评:本题考查了三角形三边关系,正确掌握三角形三边关系定理是解题关键。
17.(8分)已知a,b,c是的三边长,,,设的周长是x.
(1)求c与x的取值范围;
(2)若x是小于18的偶数,试判断的形状.
答案:(1);
(2)是等腰三角形
解析:(1)因为,,所以.
故周长x的取值范围是.
(2)因为x是小于18的偶数,
所以或.
当时,;
当时,.
当时,,为等腰三角形;
当时,,为等腰三角形.
综上,是等腰三角形.
点评:本题考查了三角形三边关系,正确掌握三角形三边关系定理是解题关键。
18.(8分)按要求完成下列各小题.
(1)在中,,,的长为偶数,求的周长;
(2)已知的三边长分别为3,5,a,化简.
答案:(1)18
(2)-3
解析:(1)根据三角形的三边关系得,即.
为偶数,,
的周长为.
(2)的三边长分别为3,5,a,
,解得,
.
点评:本题考查了三角形三边关系,正确掌握三角形三边关系定理是解题关键。
19.(8分)阅读材料:若求的值.
解:∵
根据你的观察,探究下面的问题:
(1). ,则____________________
(2).已知求的值
(3).已知的三边长都是正整数,且满足求的周长
答案:(1).
(2).
(3).∵ 则,解得, 由三角形三边关系可知,三角形三边分别为的周长为
点评:本题考查了三角形三边关系,正确掌握三角形三边关系定理是解题关键。
20.(8分)如图所示,已知是三角形内一点,连接、,试探究与的大小关系.
答案:证明:延长交于点.
在中, ,①
在中, ,②
①+②,得,
∴.
点评:本题考查了三角形三边关系,正确掌握三角形三边关系定理是解题关键。
B
C
A
D
B
C
A
D
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
人教版八年级数学上名师点拨精练
第11章 三角形
11.1.1 三角形的边
学习目标
1.认识三角形的边、内角、顶点,能用几何语言表示三角形;
2.掌握三角形的三边关系定理,能利用定理及其推论进行简单的证明;
3.了解三角形分类的原则和结论.
老师告诉你
判断三条线段能否构成三角形,只需看较短的两条线段的和是否大于第三条线段,因为只要较短的两条线段的和大于第三条线段,则任意两条线段的和都大于第三条线段,所以用此方法能很快地判断出三条线段能否构成三角形。
知识点拨
知识点1.三角形及有关概念
1.定义 由不在同一条直线上的三条线段首尾顺次相接所组成的图形叫做三角形.
构成三角形的三个基本条件:①不在同一条直线上;②三条线段;③首尾顺次相接.
2.(1)构成三角形的基本元素:
①三角形的边:即组成三角形的线段;
②三角形的角:即相邻两边所组成的角叫做三角形的内角,简称三角形的角;
③三角形的顶点:即相邻两边的公共端点.
3 .三角形的表示:三角形用符号“△”表示,顶点为A、B、C的三角形记作“△ABC”,读作“三角形ABC”,注意单独的△没有意义;△ABC的三边可以用大写字母AB、BC、AC来表示,也可以用小写字母a、b、c来表示,边BC用a表示,边AC、AB分别用b、c表示.
【新知导学】
例1-1.如图所示,图中有_____个三角形,其中以AB为边的三角形为_____,含∠OCB的三角形为_____,在△BOC中,OC的对角是_____,∠OCB的对边是_____.
【对应导练】
1.如图,图中以BC为边的三角形的个数为_____.
2.如图所示,第1个图中有1个三角形,第2个图中共有5个三角形,第3个图中共有9个三角形,依此类推,则第6个图中共有三角形_____个.
3.如图,以BD为边的三角形有哪些?分别写出来;以∠1为内角的三角形有哪些?分别写出来.
知识点2.三角形的分类
(1)按角分类:
特别强调:①锐角三角形:三个内角都是锐角的三角形; ②钝角三角形:有一个内角为钝角的三角形.
(2)按边分类:
特别强调:①等腰三角形:有两条边相等的三角形叫做等腰三角形,相等的两边都叫做腰,另外一边叫做底边,两腰的夹角叫顶角,腰与底边夹角叫做底角; ②等边三角形:三边都相等的三角形.
【新知导学】
例2-1.下列关于三角形的分类,正确的是( )
A. B.
C. D.
【对应导练】
1.三角形按边分类可以用集合来表示,如图所示,图中小椭圆圈里的A表示( )
A. 直角三角形 B. 锐角三角形
C. 钝角三角形 D. 等边三角形
2 .关于三角形的分类,有如图所示的甲、乙两种分法,则( )
A.甲、乙两种分法均正确 B.甲、乙两种分法均错误
C.甲的分法错误,乙的分法正确 D.甲的分法正确,乙的分法错误
知识点3 三角形三边关系
定理:三角形任意两边的和大于第三边(理论依据:两点之间线段最短).
推论:三角形任意两边的差小于第三边.
三边关系的应用:
判断三条线段能否组成三角形,若两条较短的线段长之和大于最长线段的长,则这三条线段可以组成三角形;反之,则不能组成三角形.当已知三角形两边长,可求第三边长的取值范围.
(2)证明线段之间的不等关系.
【新知导学】
例3-1.已知三角形两边的长分别为2cm、7cm,第三边长为整数,则第三边的长可以为( )
A. 4cm B. 5cm C. 8cm D. 9cm
【对应导练】
1.在下列长度的四条线段中,能与长6cm,8cm的两条线段围成一个三角形的是( )
A. 1cm B. 2cm C. 13cm D. 14cm
2.等腰三角形的周长为20cm,一边为8cm,则腰长为( )
A. 4cm B. 8cm C. 4cm或8cm D. 6cm或8cm
3.已知a,b,c是△ABC的三边长,满足|a-7|+(b-2)2=0,c为奇数,则△ABC的周长为 _____.
4.等腰三角形的周长为20cm,一边长为6cm,则底边长为_____cm.
5.已知a,b,c是△ABC的三边长,b,c满足(b-2)2+|c-3|=0,且a为方程|x-4|=2的解,求△ABC的周长.
二、题型训练
1.三角形的分类在判断三角形形状中的应用
1.已知a,b,c是的三边长,b,c满足,且a为方程的解,求的周长,并判断三角形的形状。
2.已知a,b,c是的三边长,,,设的周长是x.
(1)求c与x的取值范围;
(2)若x是小于18的偶数,试判断的形状.
2.三角形三边关系在拼图中的应用
3.定义:三边长和面积都是整数的三角形称为“整数三角形”.
数学学习小组的同学从32根等长的火柴棒(每根长度记为1个单位)中取出若干根,首尾依次相接组成三角形,进行探究活动.
小亮用12根火柴棒,摆成如图所示的“整数三角形”;
小颖分别用24根和30根火柴棒摆出直角“整数三角形”;
小辉受到小亮、小颖的启发,分别摆出三个不同的等腰“整数三角形”.
(1)请你画出小颖和小辉摆出的“整数三角形”的示意图;
(2)你能否也从中取出若干根摆出等边“整数三角形”,如果能,请画出示意图;如果不能,请说明理由.
3.等腰三角形的三边长分别为,,7,求等腰三角形的周长.
4.已知a,b,c为△ABC的三边长,且b,c满足,a为方程的解,求△ABC的周长,并判断△ABC的形状.
3.三角形三边关系在证明线段大小关系中的应用
5.如图,点P是△ABC内部的一点,连接PB,PC.
(1)度量线段AB,AC,PB,PC的长度,根据度量结果比较与的大小;
(2)改变点P的位置,上述结论还成立吗?
(3)你能说明上述结论为什么正确吗?
三、牛刀小试
一、单选题(每小题3分,共24分)
1.下面是一位同学用三根木棒拼成的图形,其中是三角形的是( )
A. B.
C. D.
2.下列说法正确的有( )
①等腰三角形是等边三角形;
②三角形按边分类可分为等腰三角形、等边三角形和不等边三角形;
③等腰三角形至少有两边相等;
④三角形按角分类应分为锐角三角形、直角三角形和钝角三角形.
A.①② B.①③④ C.③④ D.①②④
3.以下列各组线段为边不能组成三角形的是( )
A.3,4,4 B.2,6,8 C.2,5,4 D.6,8,10
4.设一个三角形的三边长分别为5、m、8,则m的取值范围是( )
A. B. C. D.
5.已知某等腰三角形三边长分别为5,a,11,则a的值为( )
A.5 B.5.5 C.11 D.5或11
6.设M表示直角三角形,N表示等腰三角形,P表示等边三角形,Q表示等腰直角三角形.下列四个选项中,能正确表示它们之间的关系的是( )
A. B.
C. D.
7.如图是一组按照某种规律摆放成的图形,则第5个图形中三角形的个数是( )
A.8 B.9 C.16 D.17
8.已知三角形的三边长分别为a,b,c,化简得( )
A. B. C. D.0
二、填空题(每小题4分,共20分)
9.已知等腰三角形的两边长分别为和,则它的周长是______.
10.若等腰三角形的两边长分别为6cm和8cm,则它的周长是________.
11.已知等腰三角形的周长为20,其中一边的长为6,则底边的长为_________.
12.已知a,b,c是的三条边长,则_________.
.
13.5条线段的长度分别为l cm,2 cm,3 cm,4 cm,5 cm,以其中的三条线段组成三角形,则可组成不同的三角形的个数是__________.
三、解答题(共7小题,共56分)
14.(8分)两根木棒的长分别是5cm和7cm.要选择第三根木棒,将它们首尾相接钉成一个三角形.若第三根木棒的长为偶数,则第三根木棒长的取值情况有几种
15.(8分)已知等腰三角形的两边长分别为4和10,求这个等腰三角形的周长.
16.(8分)如图,在三角形ABC中,,,D是BC的中点,E点在边AB上.
(1)若三角形BDE的周长与四边形ACDE的周长相等,求线段AE的长.
(2)若三角形ABC的周长被DE分成的两部分的差是2 cm,求线段AE的长.
17.(8分)已知a,b,c是的三边长,,,设的周长是x.
(1)求c与x的取值范围;
(2)若x是小于18的偶数,试判断的形状.
18.(8分)按要求完成下列各小题.
(1)在中,,,的长为偶数,求的周长;
(2)已知的三边长分别为3,5,a,化简.
19.(8分)阅读材料:若求的值.
解:∵
根据你的观察,探究下面的问题:
(1). ,则____________________
(2).已知求的值
(3).已知的三边长都是正整数,且满足求的周长
20.(8分)如图所示,已知是三角形内一点,连接、,试探究与的大小关系.
人教版八年级数学上名师点拨精练
第11章 三角形
11.1.1 三角形的边(解析版)
学习目标
1.认识三角形的边、内角、顶点,能用几何语言表示三角形;
2.掌握三角形的三边关系定理,能利用定理及其推论进行简单的证明;
3.了解三角形分类的原则和结论.
老师告诉你
判断三条线段能否构成三角形,只需看较短的两条线段的和是否大于第三条线段,因为只要较短的两条线段的和大于第三条线段,则任意两条线段的和都大于第三条线段,所以用此方法能很快地判断出三条线段能否构成三角形。
知识点拨
知识点1.三角形及有关概念
1.定义 由不在同一条直线上的三条线段首尾顺次相接所组成的图形叫做三角形.
构成三角形的三个基本条件:①不在同一条直线上;②三条线段;③首尾顺次相接.
2.(1)构成三角形的基本元素:
①三角形的边:即组成三角形的线段;
②三角形的角:即相邻两边所组成的角叫做三角形的内角,简称三角形的角;
③三角形的顶点:即相邻两边的公共端点.
3 .三角形的表示:三角形用符号“△”表示,顶点为A、B、C的三角形记作“△ABC”,读作“三角形ABC”,注意单独的△没有意义;△ABC的三边可以用大写字母AB、BC、AC来表示,也可以用小写字母a、b、c来表示,边BC用a表示,边AC、AB分别用b、c表示.
【新知导学】
例1-1.如图所示,图中有_____个三角形,其中以AB为边的三角形为_____,含∠OCB的三角形为_____,在△BOC中,OC的对角是_____,∠OCB的对边是_____.
【答案】(1)8;(2)△ABC,△ABD,△ABO;(3)△OCB,△ACB;(4)∠OBC;(5)OB;
【解析】根据三角形的边和角有关概念解答.
解:,图中有8个三角形,其中以AB为边的三角形为△ABC,△ABD,△ABO,含∠OCB的三角形为△OCB,△ACB,在△BOC中,OC的对角是∠OBC,∠OCB的对边是OB,
故答案为:8;△ABC,△ABD,△ABO;△OCB,△ACB;∠OBC;OB.
【对应导练】
1.如图,图中以BC为边的三角形的个数为_____.
【答案】4
【解析】根据三角形的定义即可得到结论.
解:∵以BC为公共边的三角形有△BCD,△BCE,△BCF,△ABC,
∴以BC为公共边的三角形的个数是4个.
故答案为:4.
2.如图所示,第1个图中有1个三角形,第2个图中共有5个三角形,第3个图中共有9个三角形,依此类推,则第6个图中共有三角形_____个.
【答案】21
【解析】根据前边的具体数据,再结合图形,不难发现:后边的总比前边多4,即第n个图形中,三角形的个数是1+4(n-1)=4n-3.
所以当n=6时,原式=21.注意规律:后面的图形比前面的多4个.
解:第n个图形中,三角形的个数是1+4(n-1)=4n-3.所以当n=6时,原式=21,
故答案为:21.
3.如图,以BD为边的三角形有哪些?分别写出来;以∠1为内角的三角形有哪些?分别写出来.
【分析】先根据BD边找三角形,再根据∠1找三角形.
解:以BD为边的三角形有:△BDC,△BDO,
以∠1为内角的三角形有:△EOC,△ACD.
【点拨】本题考查了三角形的内角和边的概念,学会分类的方法找三角形是本题的解题关键.
知识点2.三角形的分类
(1)按角分类:
特别强调:①锐角三角形:三个内角都是锐角的三角形; ②钝角三角形:有一个内角为钝角的三角形.
(2)按边分类:
特别强调:①等腰三角形:有两条边相等的三角形叫做等腰三角形,相等的两边都叫做腰,另外一边叫做底边,两腰的夹角叫顶角,腰与底边夹角叫做底角; ②等边三角形:三边都相等的三角形.
【新知导学】
例2-1.下列关于三角形的分类,正确的是( )
A. B.
C. D.
【答案】B
【解析】根据三角形的分类可直接选出答案.
解:A、等腰直角三角形应该是直角三角形,不符合题意;
B、该选项中的三角形的分类正确,符合题意;
C、等腰三角形包括等边三角形,不符合题意;
D、等腰三角形包括等边三角形,不符合题意;
故选:B.
【对应导练】
1.三角形按边分类可以用集合来表示,如图所示,图中小椭圆圈里的A表示( )
A. 直角三角形 B. 锐角三角形
C. 钝角三角形 D. 等边三角形
【答案】D
【解析】根据三角形的分类可直接得到答案.
解:三角形根据边分类 ,
∴图中小椭圆圈里的A表示等边三角形.
故选:D.
2 .关于三角形的分类,有如图所示的甲、乙两种分法,则( )
A.甲、乙两种分法均正确 B.甲、乙两种分法均错误
C.甲的分法错误,乙的分法正确 D.甲的分法正确,乙的分法错误
【答案】D
【分析】三角形的分类:按边分有普通三角形(三条边都不相等),等腰三角(腰与底不等的等腰三角形、腰与底相等的等腰三角形即等边三角形);按角分有直角三角形、锐角三角形、钝角三角形等,其中锐角三角形和钝角三角形统称斜三角形.据此判断即可.
【详解】解:甲分法正确,乙正确的分类应该为:
故选:D.
【点评】本题考查三角形的分类,解答的关键是熟知三角形的分类标准,易忽略等腰三角形包含等边三角形.
知识点3 三角形三边关系
定理:三角形任意两边的和大于第三边(理论依据:两点之间线段最短).
推论:三角形任意两边的差小于第三边.
三边关系的应用:
判断三条线段能否组成三角形,若两条较短的线段长之和大于最长线段的长,则这三条线段可以组成三角形;反之,则不能组成三角形.当已知三角形两边长,可求第三边长的取值范围.
(2)证明线段之间的不等关系.
【新知导学】
例3-1.已知三角形两边的长分别为2cm、7cm,第三边长为整数,则第三边的长可以为( )
A. 4cm B. 5cm C. 8cm D. 9cm
【答案】C
【解析】根据三角形的三边关系得出第三边的范围,进而得到答案.
解:设第三边的长为x cm,
则7-2<x<7+2,即5<x<9,
∵第三边的长为整数,
∴第三边的长可以为8cm.
故选:C.
【对应导练】
1.在下列长度的四条线段中,能与长6cm,8cm的两条线段围成一个三角形的是( )
A. 1cm B. 2cm C. 13cm D. 14cm
【答案】C
【解析】首先设第三条线段长为x cm,再利用三角形的三边关系可得x的范围,然后可得答案.
解:设第三条线段长为x cm,由题意得:
8-6<x<8+6,
解得:2<x<14,
只有13cm适合,
故选:C.
2.等腰三角形的周长为20cm,一边为8cm,则腰长为( )
A. 4cm B. 8cm C. 4cm或8cm D. 6cm或8cm
【答案】D
【解析】分8cm是等腰三角形的腰长与底边长两种情况进行讨论.
解:∵等腰三角形的周长为20cm,
∴当8cm是腰长时,底边=20-8-8=4cm;
∴当8cm是底边长时,腰长==6cm,
∴腰长为8cm或6cm,
故选:D.
3.已知a,b,c是△ABC的三边长,满足|a-7|+(b-2)2=0,c为奇数,则△ABC的周长为 _____.
【答案】16
【解析】根据在三角形中任意两边之和>第三边,任意两边之差<第三边;可求第三边长的范围,再根据奇数的定义得出答案.
解:∵|a-7|+(b-2)2=0,
∴a-7=0,b-2=0,
解得:a=7,b=2,
由三角形三边关系定理得:7-2<c<7+2,即5<c<9,
又∵c为奇数,
∴c=7,
∴△ABC的周长为7+2+7=16.
故答案为:16.
4.等腰三角形的周长为20cm,一边长为6cm,则底边长为_____cm.
【答案】6或8
【解析】分6cm是底边与腰长两种情况讨论求解.
解:①6cm是底边时,腰长=(20-6)=7cm,
此时三角形的三边分别为7cm、7cm、6cm,
能组成三角形,
②6cm是腰长时,底边=20-6×2=8cm,
此时三角形的三边分别为6cm、6cm、8cm,
能组成三角形,
综上所述,底边长为6或8cm.
故答案为:6或8.
5.已知a,b,c是△ABC的三边长,b,c满足(b-2)2+|c-3|=0,且a为方程|x-4|=2的解,求△ABC的周长.
【解析】利用绝对值的性质以及偶次方的性质得出b,c的值,进而利用三角形三边关系得出a的值,进而可得出其周长.
解:∵(b-2)2+|c-3|=0,
∴b-2=0,c-3=0,
解得:b=2,c=3,
∵a为方程|x-4|=2的解,
∴x-4=±2,
解得:x=6或2.
∵a、b、c为△ABC的三边长,b+c<6,
∴x=6不合题意舍去,
∴a=2,
∴△ABC的周长=a+b+c=2+2+3=7.
二、题型训练
1.三角形的分类在判断三角形形状中的应用
1.已知a,b,c是的三边长,b,c满足,且a为方程的解,求的周长,并判断三角形的形状。
答案:7,三角形是等腰三角形
解析:因为,所以,,解得,.因为a为方程的解,所以,解得或2.因为a,b,c为的三边长,所以,所以,所以的周长为.故答案为7.
a=b=2,所以三角形是等腰三角形
2.已知a,b,c是的三边长,,,设的周长是x.
(1)求c与x的取值范围;
(2)若x是小于18的偶数,试判断的形状.
答案:(1);
(2)是等腰三角形
解析:(1)因为,,所以.
故周长x的取值范围是.
(2)因为x是小于18的偶数,
所以或.
当时,;
当时,.
当时,,为等腰三角形;
当时,,为等腰三角形.
综上,是等腰三角形.
2.三角形三边关系在拼图中的应用
3.定义:三边长和面积都是整数的三角形称为“整数三角形”.
数学学习小组的同学从32根等长的火柴棒(每根长度记为1个单位)中取出若干根,首尾依次相接组成三角形,进行探究活动.
小亮用12根火柴棒,摆成如图所示的“整数三角形”;
小颖分别用24根和30根火柴棒摆出直角“整数三角形”;
小辉受到小亮、小颖的启发,分别摆出三个不同的等腰“整数三角形”.
(1)请你画出小颖和小辉摆出的“整数三角形”的示意图;
(2)你能否也从中取出若干根摆出等边“整数三角形”,如果能,请画出示意图;如果不能,请说明理由.
(1)答案:见解析
解析:小颖摆出如图1所示的“整数三角形”:
小辉摆出如图2所示三个不同的等腰“整数三角形”:
(2)答案:不能摆出等边“整数三角形”
解析:不能摆出等边“整数三角形”.理由如下:
设等边三角形的边长为a,则等边三角形面积为.
因为,若边长a为整数,那么面积一定非整数.
所以不存在等边“整数三角形”.
3.等腰三角形的三边长分别为,,7,求等腰三角形的周长.
答案:三角形的周长为19.5或23
解析:①当是底边时,则腰长为:,7,
,
,
,
等腰三角形的周长;
②当是底边时,则腰长为:,7,
,
,
,
等腰三角形的周长;
③当7是底边时,则腰长为:,,
,
,
,,
,
不能构成三角形.
则三角形的周长为19.5或23.
4.已知a,b,c为△ABC的三边长,且b,c满足,a为方程的解,求△ABC的周长,并判断△ABC的形状.
答案:因为,
所以,解得.
因为a为方程的解,所以或1.
当时,,不能构成三角形,
所以不符合题意;
当时,,能构成三角形,
此时,△ABC的周长为.
综上,△ABC的周长为17.
因为,所以△ABC是等腰三角形.
3.三角形三边关系在证明线段大小关系中的应用
5.如图,点P是△ABC内部的一点,连接PB,PC.
(1)度量线段AB,AC,PB,PC的长度,根据度量结果比较与的大小;
(2)改变点P的位置,上述结论还成立吗?
(3)你能说明上述结论为什么正确吗?
答案:(1)经度量, cm, cm, cm, cm,
所以.
(2)成立.
(3)延长BP交AC于点D.
在△ABD中,,①
在△PDC中,,②
,得,
所以.
三、牛刀小试
一、单选题(每小题3分,共24分)
1.下面是一位同学用三根木棒拼成的图形,其中是三角形的是( )
A. B.
C. D.
答案:D
解析:由不在同一条直线上的三条线段首尾顺次相接所组成的图形叫做三角形,由此可知A,B,C不是三角形,D是三角形.
故选D
2.下列说法正确的有( )
①等腰三角形是等边三角形;
②三角形按边分类可分为等腰三角形、等边三角形和不等边三角形;
③等腰三角形至少有两边相等;
④三角形按角分类应分为锐角三角形、直角三角形和钝角三角形.
A.①② B.①③④ C.③④ D.①②④
答案:C
解析:①有两条边相等的三角形是等腰三角形,三条边都相等的三角形是等边三角形,等腰三角形不一定是等边三角形,①错误;
②三角形按边分类可分为三边都不相等的三角形和等腰三角形,其中等腰三角形又可分为底边和腰不相等的三角形和等边三角形,②错误;③有两条边相等的三角形是等腰三角形,③正确;④三角形按角分类可以分为锐角三角形、直角三角形、钝角三角形,④正确.故选C.
3.以下列各组线段为边不能组成三角形的是( )
A.3,4,4 B.2,6,8 C.2,5,4 D.6,8,10
答案:B
解析:根据构成三角形条件,两边之和大于第三边,A 3+4>4.能够组成三角形,B 2+6=8,不能组成三角形,C 2+4=6>5,能够组成三角形,D 6+8=14>10,能够组成三角形。
故选B
4.设一个三角形的三边长分别为5、m、8,则m的取值范围是( )
A. B. C. D.
答案:A
解析:根据组成三角形的条件,第三边小于两边之和,大于两边之差,所以
故选A
5.已知某等腰三角形三边长分别为5,a,11,则a的值为( )
A.5 B.5.5 C.11 D.5或11
答案:C
解析:根据组成三角形的条件,第三边小于两边之和,大于两边之差,所以6
6.设M表示直角三角形,N表示等腰三角形,P表示等边三角形,Q表示等腰直角三角形.下列四个选项中,能正确表示它们之间的关系的是( )
A. B.
C. D.
答案:C
解析:根据各类三角形的概念可知,C选项可以表示它们之间的关系.故选C.
7.如图是一组按照某种规律摆放成的图形,则第5个图形中三角形的个数是( )
A.8 B.9 C.16 D.17
答案:C
解析:第1个图形中三角形的个数是1;第2个图形中三角形的个数是;第3个图形中三角形的个数是;第4个图形中三角形的个数是.由此可知,从第2个图形开始,后一个图形比前一个图形多4个三角形,因此第5个图形中三角形的个数是.故选C.
8.已知三角形的三边长分别为a,b,c,化简得( )
A. B. C. D.0
答案:A
解析:因为的三边长分别是a,b,c,所以必须满足任意两边之和大于第三边,两边之差小于第三边,则,所以.
故选A.
二、填空题(每小题4分,共20分)
9.已知等腰三角形的两边长分别为和,则它的周长是______.
答案:
解析:(1)当长为的边是等腰三角形的底边时,其三边长分别为:、、,
此时三条线段能围成等腰三角形,其周长为:;
(2)当长为的边为等腰三角形的底边时,其三边长分别为:、、,此时三条线段不能围成三角形;
综上所述,两条边长分别为和的等腰三角形的周长为
故答案为:.
点评:本题考查三角形三边关系,正确掌握三角形三边关系是解题的关键。
10.若等腰三角形的两边长分别为6cm和8cm,则它的周长是________.
答案:或
解析:等腰三角形的两条腰相等
①当腰为6cm时:三角形的周长为:;
②当腰为8cm时:三角形的周长为:;
故答案为:或.
11.已知等腰三角形的周长为20,其中一边的长为6,则底边的长为_________.
答案:6或8
解析:设底边长为x,腰长为y,
则,
①当腰长时,
,
;
三边长分别为6,6,8能构成三角形,符合题意;
故;
②当底边长时,
,
;
三边长分别为7,7,6能构成三角形,符合题意;
故;
综上所述,或;
故答案为:6或8.
12.已知a,b,c是的三条边长,则_________.
答案:2a
解析:a,b,c为的三条边长,,,原式.
13.5条线段的长度分别为l cm,2 cm,3 cm,4 cm,5 cm,以其中的三条线段组成三角形,则可组成不同的三角形的个数是__________.
答案:3
解析:以其中的三条线段为边可组成三角形的有①2 cm,3 cm,4 cm;②2 cm,4 cm,5 cm;③3 cm,4 cm,5 cm,共有3种情况故答案为3.
三、解答题(共7小题,共56分)
14.(8分)两根木棒的长分别是5cm和7cm.要选择第三根木棒,将它们首尾相接钉成一个三角形.若第三根木棒的长为偶数,则第三根木棒长的取值情况有几种
答案:第三根木棒长的取值情况有4种.
解析:设第三根木棒长度为xcm,根据题意得:
,即,
第三根木棒的长为偶数,
x可取4,6,8,10,有4种情况.
答:第三根木棒长的取值情况有4种.
点评:本题考查了三角形三边关系,正确掌握三角形三边关系定理是解题关键。
15.(8分)已知等腰三角形的两边长分别为4和10,求这个等腰三角形的周长.
答案:解:①若腰长为4,则三角形三边长为4,4,10,,不符合三角形的三边关系,故腰长不能为4;
②若腰长为10,则三角形三边长为10,10,4,符合三角形的三边关系,此时三角形的周长为24.
点评:本题考查了三角形三边关系,正确掌握三角形三边关系定理是解题关键。
16.(8分)如图,在三角形ABC中,,,D是BC的中点,E点在边AB上.
(1)若三角形BDE的周长与四边形ACDE的周长相等,求线段AE的长.
(2)若三角形ABC的周长被DE分成的两部分的差是2 cm,求线段AE的长.
答案:(1)
(2)AE的长为1 cm或3 cm
解析:(1)因为,四边形,三角形BDE的周长与四边形ACDE的周长相等,D为BC中点,
所以,,
即.
因为,,
所以,所以.
(2)由三角形ABC的周长被DE分成的两部分的差是2 cm,
可得或,
即或,
故AE的长为1 cm或3 cm.
点评:本题考查了三角形三边关系,正确掌握三角形三边关系定理是解题关键。
17.(8分)已知a,b,c是的三边长,,,设的周长是x.
(1)求c与x的取值范围;
(2)若x是小于18的偶数,试判断的形状.
答案:(1);
(2)是等腰三角形
解析:(1)因为,,所以.
故周长x的取值范围是.
(2)因为x是小于18的偶数,
所以或.
当时,;
当时,.
当时,,为等腰三角形;
当时,,为等腰三角形.
综上,是等腰三角形.
点评:本题考查了三角形三边关系,正确掌握三角形三边关系定理是解题关键。
18.(8分)按要求完成下列各小题.
(1)在中,,,的长为偶数,求的周长;
(2)已知的三边长分别为3,5,a,化简.
答案:(1)18
(2)-3
解析:(1)根据三角形的三边关系得,即.
为偶数,,
的周长为.
(2)的三边长分别为3,5,a,
,解得,
.
点评:本题考查了三角形三边关系,正确掌握三角形三边关系定理是解题关键。
19.(8分)阅读材料:若求的值.
解:∵
根据你的观察,探究下面的问题:
(1). ,则____________________
(2).已知求的值
(3).已知的三边长都是正整数,且满足求的周长
答案:(1).
(2).
(3).∵ 则,解得, 由三角形三边关系可知,三角形三边分别为的周长为
点评:本题考查了三角形三边关系,正确掌握三角形三边关系定理是解题关键。
20.(8分)如图所示,已知是三角形内一点,连接、,试探究与的大小关系.
答案:证明:延长交于点.
在中, ,①
在中, ,②
①+②,得,
∴.
点评:本题考查了三角形三边关系,正确掌握三角形三边关系定理是解题关键。
B
C
A
D
B
C
A
D
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
