人教版八年级数学上名师点拨精练第11章三角形专题一、阶段题型专训三角形三边关系八种常见应用(含解析)
文档属性
| 名称 | 人教版八年级数学上名师点拨精练第11章三角形专题一、阶段题型专训三角形三边关系八种常见应用(含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-17 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
人教版八年级数学上名师点拨精练
第11章 三角形
专题一、阶段题型专训
三角形三边关系八种常见应用
老师告诉你
三角形三边关系应用广泛,利用三角形三边关系可以判断三条线段能否组成三角形、已知两边求第三边的取值范围、求等腰三角形一边的长、求等腰三角形的周长、证明线段不等关系、化简含绝对值的式子等。
类型一、利用三角形三边关系判定三条线段能否组成三角形
例1-1.下列长度的各组线段能组成一个三角形的是( )
A. 1cm,2cm,3cm B. 3cm,8cm,5cm C. 4cm,5cm,10cm D. 4cm,5cm,6cm
针对训练1
1.若从长度分别为2 cm、3 cm、4 cm、6 cm的四根木棒中,任意选取三根首尾顺次相连搭成三角形,则搭成的不同三角形共有( )
A. 1个 B. 2个 C. 3个 D. 4个
2.平面内,将长分别为1,5,1,1,d的线段,顺次首尾相接组成凸五边形(如图),则d可能是( )
A. 1 B. 2 C. 7 D. 8
3.下列语句中,能作为“三角形两边之和大于第三边”依据的是( )
A. 三角形具有稳定性 B. 两点之间,线段最短
C. 垂线段最短 D. 三角形内角和为180°
4.已知三角形的两边长是4和6,第三边的长是方程(x-3)2=4的根,则此三角形的周长为( )
A. 17 B. 11 C. 15 D. 11或15
5.下列每组数分别是三根小木棒的长度,不能用它们搭成三角形的是( )
A. 1cm,2cm,3cm B. 2cm,3cm,4cm C. 3cm,4cm,5cm D. 5cm,6cm,7cm
类型二、利用三角形三边关系已知两边求第三边的取值范围
例2-1.若某三角形的三边长分别为3,4,m,则m的值可以是( )
A. 1 B. 5 C. 7 D. 9
针对训练2
1.已知三角形的三边长分别为4,5,x,则x不可能是( )
A. 3 B. 5 C. 7 D. 9
2.已知a,b,c是△ABC的三边长,满足|a-7|+(b-2)2=0,c为奇数,则△ABC的周长为 _____.
3.一个三角形的两边长为2和6,第三边为偶数,则这个三角形的周长为_______
4.已知三角形的三边长分别为5、a、10,则a的取值范围是 _____;如果这个三角形中有两条边相等,那么它的周长为 _____.
类型三、利用三角形三边关系求等腰三角形周长
例3-1.已知等腰三角形两边的长分别为3和7,则此等腰三角形的周长为( )
A. 13 B. 17 C. 13或17 D. 13或10
针对训练3
1 .等腰三角形的一条边长为2cm,另一条边长为5cm,则它的周长是__________cm.
若等腰三角形的一边等于5,边等于12,则它的周长是( )
A.22 B.29 C.22或29 D.17
3.已知等腰三角形的两边长是4和8,则这个三角形的周长是 _____.
4.若等腰三角形的两条边a,b满足,则等腰三角形的周长为______.
类型四、利用三角形三边关系求等腰三角形一边的长
例4-1.等腰三角形的周长为20cm,一边为8cm,则腰长为( )
A. 4cm B. 8cm C. 4cm或8cm D. 6cm或8cm
针对训练4
1.等腰三角形的周长为20cm,一边长为6cm,则底边长为_____cm.
一个等腰三角形的两边长分别为3cm,6cm,则它的腰长是( )
A.3cm B.6cm C.3cm或6cm D.5cm
类型五、利用三角形三边关系判定三角形的形状
例5-1.已知a,b,c是△ABC的三边长,满足|a-7|+(b-2)2=0,c为奇数,判断三角形的形状,并求出△ABC的周长.
针对训练5
1.一个三角形的两边长为2和6,第三边为偶数,判断三角形的形状,并求出这个三角形的周长。
2.已知a,b,c是△ABC的三边长,a,b满足|a-7|+(b-1)2=0,c为奇数,判断三角形的形状.
3.已知a,b是等腰三角形ABC的两边长,且a、b满足a2+b2+29=10a+4b,|c|=5判断这个等腰三角形的形状.
类型六、利用三角形三边关系结合中线求等腰三角形三边
例6-1.等腰三角形一腰上的中线把它的周长分为21cm和15cm的两部分,这个等腰三角形的腰长为 _____.
针对训练6
1.在△ABC中,AB=BC,中线AD将这个三角形的周长分成15和12两部分,则AC的长为( )
A.7 B.11 C.7或11 D.8或10
2.在等腰三角形ABC中,,一腰上的中线BD将这个三角形的周长分成15cm和6cm两部分,这个等腰三角形的三边长为__________
类型七、利用三角形三边关系证明线段的不等关系
例7-1.如图,D为的边BC上一点,试判断与的周长之间的大小关系,并加以证明.
针对训练7
1.如图所示,由三角形两边的和大于第三边,可得到的结论是( )
A. AB+AD>BC B. PD+CD>BP C. AB+AC>BC D. BP+CP>AC
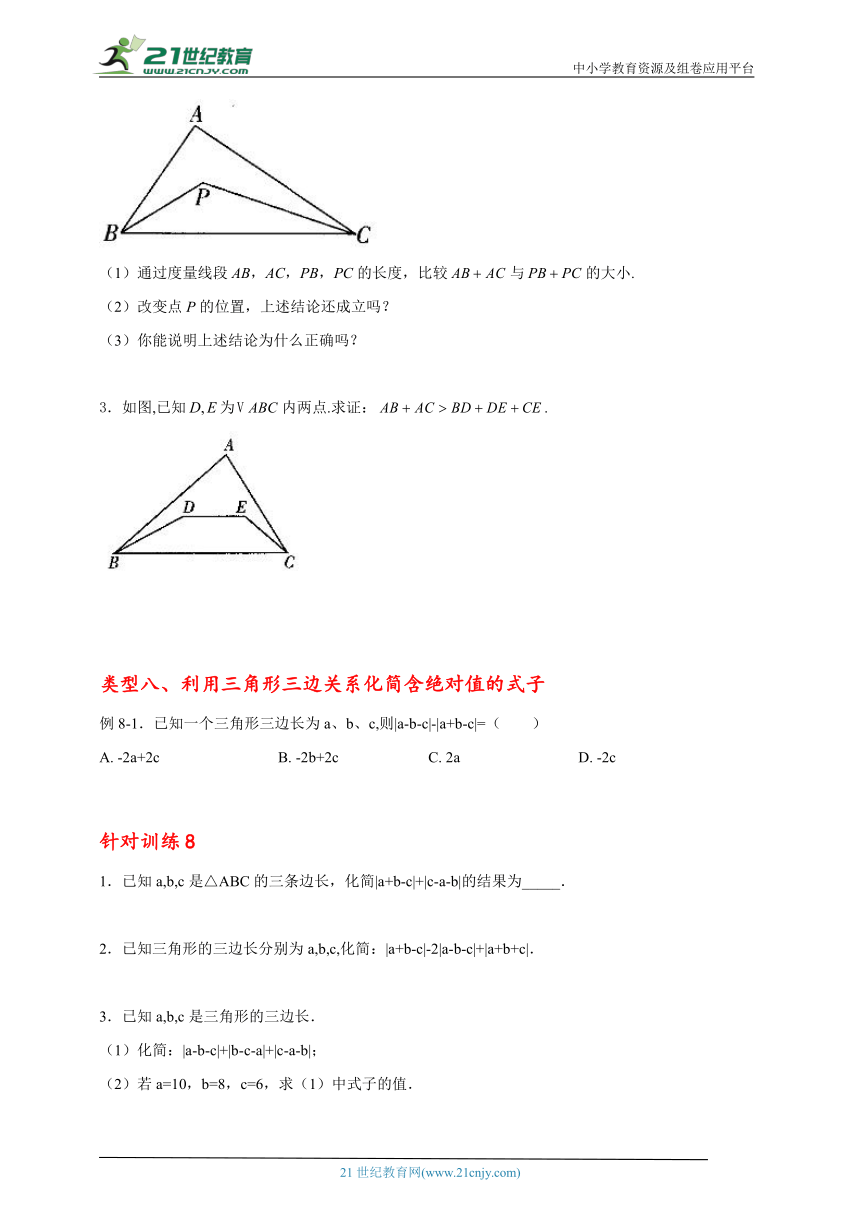
2.如图,点P是内部的一点.
(1)通过度量线段AB,AC,PB,PC的长度,比较与的大小.
(2)改变点P的位置,上述结论还成立吗?
(3)你能说明上述结论为什么正确吗?
3.如图,已知为内两点.求证:.
类型八、利用三角形三边关系化简含绝对值的式子
例8-1.已知一个三角形三边长为a、b、c,则|a-b-c|-|a+b-c|=( )
A. -2a+2c B. -2b+2c C. 2a D. -2c
针对训练8
1.已知a,b,c是△ABC的三条边长,化简|a+b-c|+|c-a-b|的结果为_____.
2.已知三角形的三边长分别为a,b,c,化简:|a+b-c|-2|a-b-c|+|a+b+c|.
3.已知a,b,c是三角形的三边长.
(1)化简:|a-b-c|+|b-c-a|+|c-a-b|;
(2)若a=10,b=8,c=6,求(1)中式子的值.
巩固练习
1.某等腰三角形的三边长分别为x,3,,则该三角形的周长为( )
A.11 B.11或8 C.11或8或5 D.与x的取值有关
3.等腰三角形的周长为13cm,其中一边长为3cm,则该等腰三角形的底边长为( )
A.7cm B.3cm C.9cm D.5cm
4.已知a、b、c是的三条边长,化简的结果为( )
A. B. C. D.0
5.三角形的两边长分别是10和8,则第三边的x取值范围是_____.
6.已知a,b,c是的三边长,b,c满足,且a为方程的解,则的周长为___________.
7.若等腰三角形的两边长分别为6cm和8cm,则它的周长是________.
8.已知等腰三角形的周长为20,其中一边的长为6,则底边的长为_________.
9.如图,由三角形两边的和大于第三边,得
___________,①
___________.②
将不等式①,②的左边、右边分别相加,得_________,③
不等式③两边都减PD,得.
10.已知的三边长分别为a,b,c.
(1)若a,b,c满足,试判断的形状;
(2)若,,且c为整数,求的周长的最大值及最小值.
11.等腰三角形一腰上的中线把该三角形的周长分为13.5 cm和11.5 cm两部分,求这个等腰三角形各边的长.
12.已知的三边长分别为a,b,c,化简.
13.等腰三角形的三边长分别为,,7,求等腰三角形的周长.
14.如图,四边形ABCD,试说明.
人教版八年级数学上名师点拨精练
第11章 三角形
专题一、阶段题型专训
三角形三边关系八种常见应用(解析版)
老师告诉你
三角形三边关系应用广泛,利用三角形三边关系可以判断三条线段能否组成三角形、已知两边求第三边的取值范围、求等腰三角形一边的长、求等腰三角形的周长、证明线段不等关系、化简含绝对值的式子等。
类型一、利用三角形三边关系判定三条线段能否组成三角形
例1-1.下列长度的各组线段能组成一个三角形的是( )
A. 1cm,2cm,3cm B. 3cm,8cm,5cm C. 4cm,5cm,10cm D. 4cm,5cm,6cm
【答案】D
【解析】根据两边之和大于第三边判断即可.
解:A、∵1+2=3,
∴长度为1cm,2cm,3cm的三条线段不能组成三角形,本选项不符合题意;
B、∵3+5=8,
∴长度为3cm,8cm,5cm的三条线段不能组成三角形,本选项不符合题意;
C、∵4+5<10,
∴长度为4cm,5cm,10cm的三条线段不能组成三角形,本选项不符合题意;
D、∵4+5>6,
∴长度为4cm,5cm,6cm的三条线段能组成三角形,本选项符合题意;
故选:D.
针对训练1
1.若从长度分别为2 cm、3 cm、4 cm、6 cm的四根木棒中,任意选取三根首尾顺次相连搭成三角形,则搭成的不同三角形共有( )
A. 1个 B. 2个 C. 3个 D. 4个
【答案】B
【解析】根据“在三角形中任意两边之和大于第三边,任意两边之差小于第三边”组合三角形.
三角形三边可以为:①2cm、3cm、4cm;②3cm、4cm、6cm.
所以,可以围成的三角形共有2个.
故选B.
【点睛】本题考查了三角形的三边关系.已知三角形的两边,则第三边的范围是:大于已知的两边的差,而小于两边的和.
2.平面内,将长分别为1,5,1,1,d的线段,顺次首尾相接组成凸五边形(如图),则d可能是( )
A. 1 B. 2 C. 7 D. 8
【答案】C
【解析】如图(见解析),设这个凸五边形为,连接,并设,先在和中,根据三角形的三边关系定理可得,,从而可得,,再在中,根据三角形的三边关系定理可得,从而可得,由此即可得出答案.
解:如图,设这个凸五边形为,连接,并设,
在中,,即,
在中,,即,
所以,,
在中,,
所以,
观察四个选项可知,只有选项C符合,
故选:C.
【点睛】本题考查了三角形的三边关系定理,通过作辅助线,构造三个三角形是解题关键.
3.下列语句中,能作为“三角形两边之和大于第三边”依据的是( )
A. 三角形具有稳定性 B. 两点之间,线段最短
C. 垂线段最短 D. 三角形内角和为180°
【答案】B
【解析】根据三角形两边之和大于第三边的推导过程三角形两边之和大于第三边的推导过程解决此题.
解:三角形两边之和大于第三边这一定理是根据“两点之间,线段最短”推导出来的.
故选:B.
4.已知三角形的两边长是4和6,第三边的长是方程(x-3)2=4的根,则此三角形的周长为( )
A. 17 B. 11 C. 15 D. 11或15
【答案】C
【解析】求出方程的解得到原方程的解,即可能为三角形的第三边,然后利用三角形的两边之和大于第三边判断能否构成三角形,选择满足题意的第三边,即可求出三角形的周长.
解:(x-3)2=4,
x-3=±2,
解得x1=5,x2=1.
若x=5,则三角形的三边分别为4,5,6,其周长为4+5+6=15;
若x=1时,6-4=2,不能构成三角形,
则此三角形的周长是15.
故选:C.
5.下列每组数分别是三根小木棒的长度,不能用它们搭成三角形的是( )
A. 1cm,2cm,3cm B. 2cm,3cm,4cm C. 3cm,4cm,5cm D. 5cm,6cm,7cm
【答案】A
【解析】用三角形两边之和大于第三边,两边只差小于第三边进行判断.
解:∵三角形两边之和大于第三边,两边只差小于第三边,
∴组成三角形的线段需满足两条线段的和大于第三条线段,
A、1cm+2cm=3cm,不能搭成三角形,故A符合题意,
B、2cm+3cm>4cm,3cm-2cm<4cm,能搭成三角形,故B不符合题意,
C、3cm+4cm>5cm,4cm-3cm<5cm,能搭成三角形,故C不符合题意,
D、5cm+6cm>7cm,6cm-5cm<7cm,能搭成三角形,故C不符合题意,
故选:A.
类型二、利用三角形三边关系已知两边求第三边的取值范围
例2-1.若某三角形的三边长分别为3,4,m,则m的值可以是( )
A. 1 B. 5 C. 7 D. 9
【答案】B
【解析】根据三角形的三边关系定理得出4-3<m<4+3,求出即可.
解:根据三角形的三边关系定理得:4-3<m<4+3,
解得:1<m<7,
即符合的只有5,
故选:B.
针对训练2
1.已知三角形的三边长分别为4,5,x,则x不可能是( )
A. 3 B. 5 C. 7 D. 9
【答案】D
【解析】已知两边时,第三边的范围是大于两边的差,小于两边的和.这样就可以确定x的范围,也就可以求出x的不可能取得的值.
解:5-4<x<5+4,即1<x<9,则x的不可能的值是9,
故选:D.
2.已知a,b,c是△ABC的三边长,满足|a-7|+(b-2)2=0,c为奇数,则△ABC的周长为 _____.
【答案】16
【解析】根据在三角形中任意两边之和>第三边,任意两边之差<第三边;可求第三边长的范围,再根据奇数的定义得出答案.
解:∵|a-7|+(b-2)2=0,
∴a-7=0,b-2=0,
解得:a=7,b=2,
由三角形三边关系定理得:7-2<c<7+2,即5<c<9,
又∵c为奇数,
∴c=7,
∴△ABC的周长为7+2+7=16.
故答案为:16.
3.一个三角形的两边长为2和6,第三边为偶数,则这个三角形的周长为_______
【答案】14
【解析】根据在三角形中任意两边之和大于第三边,任意两边之差小于第三边.即可求解.
解:第三边的取值范围是大于4且小于8,又第三边是偶数,
故第三边是6.
∴该三角形的周长是:2+6+6=14.
故答案为:14.
【点睛】首先根据三角形的三边关系确定第三边的取值范围,再根据第三边是偶数确定第三边的长.
4.已知三角形的三边长分别为5、a、10,则a的取值范围是 _____;如果这个三角形中有两条边相等,那么它的周长为 _____.
【答案】(1)5<a<15;(2)25;
【解析】根据三角形的三边关系可得8-4<a<8+4,再解即可得到a的取值范围;根据三角形的三边关系结合已知条件可得a=8,然后求周长即可.
解:根据三角形的三边关系可得:
10-5<a<10+5,
即5<a<15,
∵这个三角形中有两条边相等,
∴a=10或a=5(不符合三角形的三边关系,不合题意,舍去)
∴周长为5+10+10=25,
故答案为:5<a<15;25.
类型三、利用三角形三边关系求等腰三角形周长
例3-1.已知等腰三角形两边的长分别为3和7,则此等腰三角形的周长为( )
A. 13 B. 17 C. 13或17 D. 13或10
【答案】B
【解析】等腰三角形两边的长为3和7,具体哪条是底边,哪条是腰没有明确说明,因此要分两种情况讨论.
解:①当腰是3,底边是7时,3+3<7不满足三角形的三边关系,因此舍去.
②当底边是3,腰长是7时,7+7>3能构成三角形,则其周长=3+7+7=17.
故选:B.
【点睛】本题考查了等腰三角形的性质和三角形的三边关系,解题时注意:若没有明确腰和底边,则一定要分类进行讨论,还应验证各种情况是否能构成三角形,这是解题的关键.
针对训练3
1 .等腰三角形的一条边长为2cm,另一条边长为5cm,则它的周长是__________cm.
答案:12
解析:①当2cm为底时, 其它两边都为5cm,2cm,5cm,5cm可以构成三角形,
周长为12cm;
②当2cm为腰时,
其它两边为2cm和5cm,
不能构成三角形,故舍去,
故答案为:12.
若等腰三角形的一边等于5,边等于12,则它的周长是( )
A.22 B.29 C.22或29 D.17
答案:B
解析:若5为底边长,12为腰长,
,
能组成三角形,此时它的周长是:;
若12为底边长,5为腰长,
,
不能组成三角形,故舍去.
它的周长是29.
故选:B.
3.已知等腰三角形的两边长是4和8,则这个三角形的周长是 _____.
【答案】20
【解析】分两种情况:当等腰三角形的腰长为4,底边长为8时;当等腰三角形的腰长为8,底边长为4时;然后分别进行计算即可解答.
解:分两种情况:
当等腰三角形的腰长为4,底边长为8时,
∵4+4=8,
∴不能组成三角形;
当等腰三角形的腰长为8,底边长为4时,
∴等腰三角形的周长=8+8+4=20;
综上所述:这个三角形的周长是20,
故答案为:20.
4.若等腰三角形的两条边a,b满足,则等腰三角形的周长为______.
【答案】4+或2+
【解析】根据二次根式有意义,可得a=2,代入求得b=,利用三边关系求周长即可.
解:由题意,得3a-6≥0,2-a≥0
∴a=2
将a=2代入,得b=
当腰为2时,符合三角形三边关系,周长为4+
当腰为时,符合三角形三边关系,周长为2+
故答案为:4+或2+
【点睛】本题主要考查二次根式有意义的条件,以及三角形三边关系求周长的问题,利用二次根式有意义的条件得出a值是解题关键.
类型四、利用三角形三边关系求等腰三角形一边的长
例4-1.等腰三角形的周长为20cm,一边为8cm,则腰长为( )
A. 4cm B. 8cm C. 4cm或8cm D. 6cm或8cm
【答案】D
【解析】分8cm是等腰三角形的腰长与底边长两种情况进行讨论.
解:∵等腰三角形的周长为20cm,
∴当8cm是腰长时,底边=20-8-8=4cm;
∴当8cm是底边长时,腰长==6cm,
∴腰长为8cm或6cm,
故选:D.
针对训练4
1.等腰三角形的周长为20cm,一边长为6cm,则底边长为_____cm.
【答案】6或8
【解析】分6cm是底边与腰长两种情况讨论求解.
解:①6cm是底边时,腰长=(20-6)=7cm,
此时三角形的三边分别为7cm、7cm、6cm,
能组成三角形,
②6cm是腰长时,底边=20-6×2=8cm,
此时三角形的三边分别为6cm、6cm、8cm,
能组成三角形,
综上所述,底边长为6或8cm.
故答案为:6或8.
一个等腰三角形的两边长分别为3cm,6cm,则它的腰长是( )
A.3cm B.6cm C.3cm或6cm D.5cm
答案:B
解析:分两种情况考虑:
若3cm为等腰三角形的腰长,则三边分别为3cm,3cm,6cm,,不符合题意,舍去;
若6cm为等腰三角形的腰长,则三边分别为6cm,6cm,3cm,符合题意,
则它的腰长是6cm.
故选:B.
类型五、利用三角形三边关系判定三角形的形状
例5-1.已知a,b,c是△ABC的三边长,满足|a-7|+(b-2)2=0,c为奇数,判断三角形的形状,并求出△ABC的周长.
【答案】 等腰三角形,16
【解析】根据在三角形中任意两边之和>第三边,任意两边之差<第三边;可求第三边长的范围,再根据奇数的定义得出答案.
解:∵|a-7|+(b-2)2=0,
∴a-7=0,b-2=0,
解得:a=7,b=2,
由三角形三边关系定理得:7-2<c<7+2,即5<c<9,
又∵c为奇数,
∴c=7,
所以△ABC是等腰三角形
∴△ABC的周长为7+2+7=16.
故答案为:等腰三角形,16.
针对训练5
1.一个三角形的两边长为2和6,第三边为偶数,判断三角形的形状,并求出这个三角形的周长。
【答案】 等腰三角形 14
【解析】根据在三角形中任意两边之和大于第三边,任意两边之差小于第三边.即可求解.
解:第三边的取值范围是大于4且小于8,又第三边是偶数,
故第三边是6.
所以该三角形是等腰三角形
∴该三角形的周长是:2+6+6=14.
故答案为:等腰三角形 14.
【点睛】首先根据三角形的三边关系确定第三边的取值范围,再根据第三边是偶数确定第三边的长.
2.已知a,b,c是△ABC的三边长,a,b满足|a-7|+(b-1)2=0,c为奇数,判断三角形的形状.
【答案】等腰三角形
【解析】根据非负数的性质列式求出a、b的值,再根据三角形的任意两边之和大于第三边,两边之差小于第三边求出c的取值范围,再根据c是奇数求出c的值.
解:∵a,b满足|a-7|+(b-1)2=0,
∴a-7=0,b-1=0,
解得a=7,b=1,
∵7-1=6,7+1=8,
∴6<c<8,
又∵c为奇数,
∴c=7,
所以三角形是等腰三角形
3.已知a,b是等腰三角形ABC的两边长,且a、b满足a2+b2+29=10a+4b,|c|=5判断这个等腰三角形的形状.
【答案】等腰三角形
【解析】利用配方法分别求出a、b,根据三角形三边关系判断
解:a2+b2+29=10a+4b,
a2-10a+25+b2-4b+4=0,
(a-5)2+(b-2)2=0,
a-5=0,b-2=0,
解得,a=5,b=2,
|c|=5
C=5
∴这个三角形是等腰三角形
类型六、利用三角形三边关系结合中线求等腰三角形三边
例6-1.等腰三角形一腰上的中线把它的周长分为21cm和15cm的两部分,这个等腰三角形的腰长为 _____.
【答案】14cm或10cm
【解析】根据题意可知腰与底的差为6,结合等腰三角形的周长为36,可求得腰长.
解:设腰长为x cm,底为y cm,
根据题意可知x-y=21-15=6(cm)或y-x=6(cm),
且x+x+y=36,
当x-y=6时,可解得x=14,此时三角形的三边为14、14、8,满足三角形的三边关系;
当y-x=6时,可解得x=10,此时三角形的三边为10、10、16,满足三角形的三边关系;
综上可知,三角形的腰长为14cm或10cm.
故答案为:14cm或10cm.
针对训练6
1.在△ABC中,AB=BC,中线AD将这个三角形的周长分成15和12两部分,则AC的长为( )
A.7 B.11 C.7或11 D.8或10
【答案】C
【分析】设AB=BC=2x,AC=y,则BD=CD=x,根据周长分成两部分可得分两种情况讨论即可,注意三角形三边关系的应用.
解:设AB=BC=2x,AC=y,
∵AD为BC边上的中线,
∴则BD=CD=x,
∵中线AD将这个三角形的周长分成15和12两部分,
∴当AB+BD=15,且AC+CD=12时,
则2x+x=15,且y+x=12,
由2x+x=15解得:x=5,
∴y+5=12,
解得:y=7,
∴三边长分别为10,10,7(符合题意),
∴AC=7;
当AB+BD=12,且AC+CD=15时,
则2x+x=12,且y+x=15,
由2x+x=12解得:x=4,
∴y+4=15,
解得:y=11,
∴三边长分别为8,8,11(符合题意),
∴AC=11,
综上所述:AC的长为7或11,
故选:C.
【点拨】本题考查了三角形的中线以及三角形三边关系,注意要分两种情况讨论是正确解答本题的关键.
2.在等腰三角形ABC中,,一腰上的中线BD将这个三角形的周长分成15cm和6cm两部分,这个等腰三角形的三边长为__________
答案:10cm,10cm,1cm
解析:设,,则,
AC上的中线BD将这个三角形的周长分成15和6两部分,
有两种情况:
(1)当,且,
解得:,,
三边长分别为10cm,10cm,1cm;
(2)当且时,
解得:,,此时腰长为4,
根据三角形三边关系,任意两边之和大于第三边,而,
故这种情况不存在.
腰长只能是10cm.
故答案为:10cm,10cm,1cm.
类型七、利用三角形三边关系证明线段的不等关系
例7-1.如图,D为的边BC上一点,试判断与的周长之间的大小关系,并加以证明.
答案:的周长,见解析
解析:证明:在中,,
在中,,
,
即,
的周长
针对训练7
1.如图所示,由三角形两边的和大于第三边,可得到的结论是( )
A. AB+AD>BC B. PD+CD>BP C. AB+AC>BC D. BP+CP>AC
【答案】C
【解析】利用三角形的三边关系进行分析即可.
解:在△ABC中,AB+AC>BC,
故选:C.
2.如图,点P是内部的一点.
(1)通过度量线段AB,AC,PB,PC的长度,比较与的大小.
(2)改变点P的位置,上述结论还成立吗?
(3)你能说明上述结论为什么正确吗?
答案:(1).
(2)成立.
(3)见解析
解析:解:(3)延长BP交AC于点D.
在中,,①
在中,,②
①+②得,
所以.
3.如图,已知为内两点.求证:.
答案:如图,延长,分别交于点,交于点.
在中,.
在中,.
在中,.
,
.
又,
.
类型八、利用三角形三边关系化简含绝对值的式子
例8-1.已知一个三角形三边长为a、b、c,则|a-b-c|-|a+b-c|=( )
A. -2a+2c B. -2b+2c C. 2a D. -2c
【答案】A
【解析】根据三角形的三边关系得到b+c>a,a+b>c,根据绝对值的性质、合并同类项法则计算,得到答案.
解:∵a、b、c是一个三角形三边长,
∴b+c>a,a+b>c,
∴|a-b-c|-|a+b-c|
=-(a-b-c)-(a+b-c)
=-a+b+c-a-b+c
=-2a+2c,
故选:A.
针对训练8
1.已知a,b,c是△ABC的三条边长,化简|a+b-c|+|c-a-b|的结果为_____.
【答案】2a+2b-2c
【解析】先根据三角形的三边关系判断出a+b-c与c-b-a的符号,再去绝对值符号,合并同类项即可;
解:∵a、b、c为△ABC的三条边长,
∴a+b-c>0,c-a-b<0,
∴原式=a+b-c-(c-a-b)
=a+b-c-c+a+b
=2a+2b-2c
故答案为:2a+2b-2c.
2.已知三角形的三边长分别为a,b,c,化简:|a+b-c|-2|a-b-c|+|a+b+c|.
【解析】三角形三边满足的条件是:两边和大于第三边,两边的差小于第三边,根据此条件来确定绝对值内的式子的正负,从而化简计算即可.
解:∵△ABC的三边长分别是a、b、c,
∴必须满足两边之和大于第三边,两边的差小于第三边,则a+b-c>0,a-b-c<0,a+b+c>0,
∴|a+b-c|-2|a-b-c|+|a+b+c|=a+b-c+2a-2b-2c+a+b+c=4a-2c.
3.已知a,b,c是三角形的三边长.
(1)化简:|a-b-c|+|b-c-a|+|c-a-b|;
(2)若a=10,b=8,c=6,求(1)中式子的值.
【解析】(1)根据三角形的三边关系,两边之和大于第三边,即可确定绝对值符号内的式子的符号,从而去掉绝对值符号,然后进行化简即可;
(2)代人a=10,b=8,c=6求值即可.
解:(1)∵a,b,c是三角形的三边长,
∴b+c>a,c+a>b,a+b>c,
∴a-b-c<0,b-c-a<0,c-a-b<0,
∴|a-b-c|+|b-c-a|+|c-a-b|=b+c-a+c+a-b+a+b-c=a+b+c.
(2)把a=10,b=8,c=6代入(1)中式子,得原式=10+8+6=24.
巩固练习
1.某等腰三角形的三边长分别为x,3,,则该三角形的周长为( )
A.11 B.11或8 C.11或8或5 D.与x的取值有关
答案:B
解析:当时,此时,,能组成三角形,此时三角形的周长为.当时,此时,,不能组成三角形.当时,此时,,能组成三角形,此时三角形的周长为.
2.已知三角形的三边长分别为3、4、x,则x不可能是( )
A.4 B.5 C.6 D.7
答案:D
解析:,,
.
观察四个选项,x不可能是7.
故选:D.
3.等腰三角形的周长为13cm,其中一边长为3cm,则该等腰三角形的底边长为( )
A.7cm B.3cm C.9cm D.5cm
答案:B
解析:当长是3cm的边是底边时,
三边为3cm,5cm,5cm,等腰三角形成立;
当长是3cm的边是腰时,底边长是:,
而,不满足三角形的三边关系;
故底边长是:3cm.
故选:B.
4.已知a、b、c是的三条边长,化简的结果为( )
A. B. C. D.0
答案:D
解析:a、b、c为的三条边长,
,,
原式.
故选:D.
5.三角形的两边长分别是10和8,则第三边的x取值范围是_____.
答案:
解析:根据三角形的三边关系:,
解得:.
故答案为:.
6.已知a,b,c是的三边长,b,c满足,且a为方程的解,则的周长为___________.
答案:7
解析:因为,所以,,解得,.因为a为方程的解,所以,解得或2.因为a,b,c为的三边长,所以,所以,所以的周长为.
故答案为7.
7.若等腰三角形的两边长分别为6cm和8cm,则它的周长是________.
答案:或
解析:等腰三角形的两条腰相等
①当腰为6cm时:三角形的周长为:;
②当腰为8cm时:三角形的周长为:;
故答案为:或.
8.已知等腰三角形的周长为20,其中一边的长为6,则底边的长为_________.
答案:6或8
解析:设底边长为x,腰长为y,
则,
①当腰长时,
,
;
三边长分别为6,6,8能构成三角形,符合题意;
故;
②当底边长时,
,
;
三边长分别为7,7,6能构成三角形,符合题意;
故;
综上所述,或;
故答案为:6或8.
9.如图,由三角形两边的和大于第三边,得
___________,①
___________.②
将不等式①,②的左边、右边分别相加,得_________,③
不等式③两边都减PD,得.
答案:;;
解析:由三角形两边的和大于第三边,得,.将不等式左边、右边分别相加,得,即.
10.已知的三边长分别为a,b,c.
(1)若a,b,c满足,试判断的形状;
(2)若,,且c为整数,求的周长的最大值及最小值.
答案:(1),
,,,
是等边三角形.
(2),,,即,又c为整数,
,5,6,
当时,的周长最小,最小值;
当时,的周长最大,最大值.
11.等腰三角形一腰上的中线把该三角形的周长分为13.5 cm和11.5 cm两部分,求这个等腰三角形各边的长.
答案:设在中,,BD是AC边上的中线,
依题意,当时,,,
所以,
解得.
当时,,
.所以,
解得.
综上,这个等腰三角形三边的长分别为9cm,9cm,7cm或.
12.已知的三边长分别为a,b,c,化简.
答案:
解析:a,b,c是的三边长,
,,
.
13.等腰三角形的三边长分别为,,7,求等腰三角形的周长.
答案:三角形的周长为19.5或23
解析:①当是底边时,则腰长为:,7,
,
,
,
等腰三角形的周长;
②当是底边时,则腰长为:,7,
,
,
,
等腰三角形的周长;
③当7是底边时,则腰长为:,,
,
,
,,
,
不能构成三角形.
则三角形的周长为19.5或23.
14.如图,四边形ABCD,试说明.
答案:如图,延长BD交AC于点E.
因为,
所以.
因为,
所以.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
人教版八年级数学上名师点拨精练
第11章 三角形
专题一、阶段题型专训
三角形三边关系八种常见应用
老师告诉你
三角形三边关系应用广泛,利用三角形三边关系可以判断三条线段能否组成三角形、已知两边求第三边的取值范围、求等腰三角形一边的长、求等腰三角形的周长、证明线段不等关系、化简含绝对值的式子等。
类型一、利用三角形三边关系判定三条线段能否组成三角形
例1-1.下列长度的各组线段能组成一个三角形的是( )
A. 1cm,2cm,3cm B. 3cm,8cm,5cm C. 4cm,5cm,10cm D. 4cm,5cm,6cm
针对训练1
1.若从长度分别为2 cm、3 cm、4 cm、6 cm的四根木棒中,任意选取三根首尾顺次相连搭成三角形,则搭成的不同三角形共有( )
A. 1个 B. 2个 C. 3个 D. 4个
2.平面内,将长分别为1,5,1,1,d的线段,顺次首尾相接组成凸五边形(如图),则d可能是( )
A. 1 B. 2 C. 7 D. 8
3.下列语句中,能作为“三角形两边之和大于第三边”依据的是( )
A. 三角形具有稳定性 B. 两点之间,线段最短
C. 垂线段最短 D. 三角形内角和为180°
4.已知三角形的两边长是4和6,第三边的长是方程(x-3)2=4的根,则此三角形的周长为( )
A. 17 B. 11 C. 15 D. 11或15
5.下列每组数分别是三根小木棒的长度,不能用它们搭成三角形的是( )
A. 1cm,2cm,3cm B. 2cm,3cm,4cm C. 3cm,4cm,5cm D. 5cm,6cm,7cm
类型二、利用三角形三边关系已知两边求第三边的取值范围
例2-1.若某三角形的三边长分别为3,4,m,则m的值可以是( )
A. 1 B. 5 C. 7 D. 9
针对训练2
1.已知三角形的三边长分别为4,5,x,则x不可能是( )
A. 3 B. 5 C. 7 D. 9
2.已知a,b,c是△ABC的三边长,满足|a-7|+(b-2)2=0,c为奇数,则△ABC的周长为 _____.
3.一个三角形的两边长为2和6,第三边为偶数,则这个三角形的周长为_______
4.已知三角形的三边长分别为5、a、10,则a的取值范围是 _____;如果这个三角形中有两条边相等,那么它的周长为 _____.
类型三、利用三角形三边关系求等腰三角形周长
例3-1.已知等腰三角形两边的长分别为3和7,则此等腰三角形的周长为( )
A. 13 B. 17 C. 13或17 D. 13或10
针对训练3
1 .等腰三角形的一条边长为2cm,另一条边长为5cm,则它的周长是__________cm.
若等腰三角形的一边等于5,边等于12,则它的周长是( )
A.22 B.29 C.22或29 D.17
3.已知等腰三角形的两边长是4和8,则这个三角形的周长是 _____.
4.若等腰三角形的两条边a,b满足,则等腰三角形的周长为______.
类型四、利用三角形三边关系求等腰三角形一边的长
例4-1.等腰三角形的周长为20cm,一边为8cm,则腰长为( )
A. 4cm B. 8cm C. 4cm或8cm D. 6cm或8cm
针对训练4
1.等腰三角形的周长为20cm,一边长为6cm,则底边长为_____cm.
一个等腰三角形的两边长分别为3cm,6cm,则它的腰长是( )
A.3cm B.6cm C.3cm或6cm D.5cm
类型五、利用三角形三边关系判定三角形的形状
例5-1.已知a,b,c是△ABC的三边长,满足|a-7|+(b-2)2=0,c为奇数,判断三角形的形状,并求出△ABC的周长.
针对训练5
1.一个三角形的两边长为2和6,第三边为偶数,判断三角形的形状,并求出这个三角形的周长。
2.已知a,b,c是△ABC的三边长,a,b满足|a-7|+(b-1)2=0,c为奇数,判断三角形的形状.
3.已知a,b是等腰三角形ABC的两边长,且a、b满足a2+b2+29=10a+4b,|c|=5判断这个等腰三角形的形状.
类型六、利用三角形三边关系结合中线求等腰三角形三边
例6-1.等腰三角形一腰上的中线把它的周长分为21cm和15cm的两部分,这个等腰三角形的腰长为 _____.
针对训练6
1.在△ABC中,AB=BC,中线AD将这个三角形的周长分成15和12两部分,则AC的长为( )
A.7 B.11 C.7或11 D.8或10
2.在等腰三角形ABC中,,一腰上的中线BD将这个三角形的周长分成15cm和6cm两部分,这个等腰三角形的三边长为__________
类型七、利用三角形三边关系证明线段的不等关系
例7-1.如图,D为的边BC上一点,试判断与的周长之间的大小关系,并加以证明.
针对训练7
1.如图所示,由三角形两边的和大于第三边,可得到的结论是( )
A. AB+AD>BC B. PD+CD>BP C. AB+AC>BC D. BP+CP>AC
2.如图,点P是内部的一点.
(1)通过度量线段AB,AC,PB,PC的长度,比较与的大小.
(2)改变点P的位置,上述结论还成立吗?
(3)你能说明上述结论为什么正确吗?
3.如图,已知为内两点.求证:.
类型八、利用三角形三边关系化简含绝对值的式子
例8-1.已知一个三角形三边长为a、b、c,则|a-b-c|-|a+b-c|=( )
A. -2a+2c B. -2b+2c C. 2a D. -2c
针对训练8
1.已知a,b,c是△ABC的三条边长,化简|a+b-c|+|c-a-b|的结果为_____.
2.已知三角形的三边长分别为a,b,c,化简:|a+b-c|-2|a-b-c|+|a+b+c|.
3.已知a,b,c是三角形的三边长.
(1)化简:|a-b-c|+|b-c-a|+|c-a-b|;
(2)若a=10,b=8,c=6,求(1)中式子的值.
巩固练习
1.某等腰三角形的三边长分别为x,3,,则该三角形的周长为( )
A.11 B.11或8 C.11或8或5 D.与x的取值有关
3.等腰三角形的周长为13cm,其中一边长为3cm,则该等腰三角形的底边长为( )
A.7cm B.3cm C.9cm D.5cm
4.已知a、b、c是的三条边长,化简的结果为( )
A. B. C. D.0
5.三角形的两边长分别是10和8,则第三边的x取值范围是_____.
6.已知a,b,c是的三边长,b,c满足,且a为方程的解,则的周长为___________.
7.若等腰三角形的两边长分别为6cm和8cm,则它的周长是________.
8.已知等腰三角形的周长为20,其中一边的长为6,则底边的长为_________.
9.如图,由三角形两边的和大于第三边,得
___________,①
___________.②
将不等式①,②的左边、右边分别相加,得_________,③
不等式③两边都减PD,得.
10.已知的三边长分别为a,b,c.
(1)若a,b,c满足,试判断的形状;
(2)若,,且c为整数,求的周长的最大值及最小值.
11.等腰三角形一腰上的中线把该三角形的周长分为13.5 cm和11.5 cm两部分,求这个等腰三角形各边的长.
12.已知的三边长分别为a,b,c,化简.
13.等腰三角形的三边长分别为,,7,求等腰三角形的周长.
14.如图,四边形ABCD,试说明.
人教版八年级数学上名师点拨精练
第11章 三角形
专题一、阶段题型专训
三角形三边关系八种常见应用(解析版)
老师告诉你
三角形三边关系应用广泛,利用三角形三边关系可以判断三条线段能否组成三角形、已知两边求第三边的取值范围、求等腰三角形一边的长、求等腰三角形的周长、证明线段不等关系、化简含绝对值的式子等。
类型一、利用三角形三边关系判定三条线段能否组成三角形
例1-1.下列长度的各组线段能组成一个三角形的是( )
A. 1cm,2cm,3cm B. 3cm,8cm,5cm C. 4cm,5cm,10cm D. 4cm,5cm,6cm
【答案】D
【解析】根据两边之和大于第三边判断即可.
解:A、∵1+2=3,
∴长度为1cm,2cm,3cm的三条线段不能组成三角形,本选项不符合题意;
B、∵3+5=8,
∴长度为3cm,8cm,5cm的三条线段不能组成三角形,本选项不符合题意;
C、∵4+5<10,
∴长度为4cm,5cm,10cm的三条线段不能组成三角形,本选项不符合题意;
D、∵4+5>6,
∴长度为4cm,5cm,6cm的三条线段能组成三角形,本选项符合题意;
故选:D.
针对训练1
1.若从长度分别为2 cm、3 cm、4 cm、6 cm的四根木棒中,任意选取三根首尾顺次相连搭成三角形,则搭成的不同三角形共有( )
A. 1个 B. 2个 C. 3个 D. 4个
【答案】B
【解析】根据“在三角形中任意两边之和大于第三边,任意两边之差小于第三边”组合三角形.
三角形三边可以为:①2cm、3cm、4cm;②3cm、4cm、6cm.
所以,可以围成的三角形共有2个.
故选B.
【点睛】本题考查了三角形的三边关系.已知三角形的两边,则第三边的范围是:大于已知的两边的差,而小于两边的和.
2.平面内,将长分别为1,5,1,1,d的线段,顺次首尾相接组成凸五边形(如图),则d可能是( )
A. 1 B. 2 C. 7 D. 8
【答案】C
【解析】如图(见解析),设这个凸五边形为,连接,并设,先在和中,根据三角形的三边关系定理可得,,从而可得,,再在中,根据三角形的三边关系定理可得,从而可得,由此即可得出答案.
解:如图,设这个凸五边形为,连接,并设,
在中,,即,
在中,,即,
所以,,
在中,,
所以,
观察四个选项可知,只有选项C符合,
故选:C.
【点睛】本题考查了三角形的三边关系定理,通过作辅助线,构造三个三角形是解题关键.
3.下列语句中,能作为“三角形两边之和大于第三边”依据的是( )
A. 三角形具有稳定性 B. 两点之间,线段最短
C. 垂线段最短 D. 三角形内角和为180°
【答案】B
【解析】根据三角形两边之和大于第三边的推导过程三角形两边之和大于第三边的推导过程解决此题.
解:三角形两边之和大于第三边这一定理是根据“两点之间,线段最短”推导出来的.
故选:B.
4.已知三角形的两边长是4和6,第三边的长是方程(x-3)2=4的根,则此三角形的周长为( )
A. 17 B. 11 C. 15 D. 11或15
【答案】C
【解析】求出方程的解得到原方程的解,即可能为三角形的第三边,然后利用三角形的两边之和大于第三边判断能否构成三角形,选择满足题意的第三边,即可求出三角形的周长.
解:(x-3)2=4,
x-3=±2,
解得x1=5,x2=1.
若x=5,则三角形的三边分别为4,5,6,其周长为4+5+6=15;
若x=1时,6-4=2,不能构成三角形,
则此三角形的周长是15.
故选:C.
5.下列每组数分别是三根小木棒的长度,不能用它们搭成三角形的是( )
A. 1cm,2cm,3cm B. 2cm,3cm,4cm C. 3cm,4cm,5cm D. 5cm,6cm,7cm
【答案】A
【解析】用三角形两边之和大于第三边,两边只差小于第三边进行判断.
解:∵三角形两边之和大于第三边,两边只差小于第三边,
∴组成三角形的线段需满足两条线段的和大于第三条线段,
A、1cm+2cm=3cm,不能搭成三角形,故A符合题意,
B、2cm+3cm>4cm,3cm-2cm<4cm,能搭成三角形,故B不符合题意,
C、3cm+4cm>5cm,4cm-3cm<5cm,能搭成三角形,故C不符合题意,
D、5cm+6cm>7cm,6cm-5cm<7cm,能搭成三角形,故C不符合题意,
故选:A.
类型二、利用三角形三边关系已知两边求第三边的取值范围
例2-1.若某三角形的三边长分别为3,4,m,则m的值可以是( )
A. 1 B. 5 C. 7 D. 9
【答案】B
【解析】根据三角形的三边关系定理得出4-3<m<4+3,求出即可.
解:根据三角形的三边关系定理得:4-3<m<4+3,
解得:1<m<7,
即符合的只有5,
故选:B.
针对训练2
1.已知三角形的三边长分别为4,5,x,则x不可能是( )
A. 3 B. 5 C. 7 D. 9
【答案】D
【解析】已知两边时,第三边的范围是大于两边的差,小于两边的和.这样就可以确定x的范围,也就可以求出x的不可能取得的值.
解:5-4<x<5+4,即1<x<9,则x的不可能的值是9,
故选:D.
2.已知a,b,c是△ABC的三边长,满足|a-7|+(b-2)2=0,c为奇数,则△ABC的周长为 _____.
【答案】16
【解析】根据在三角形中任意两边之和>第三边,任意两边之差<第三边;可求第三边长的范围,再根据奇数的定义得出答案.
解:∵|a-7|+(b-2)2=0,
∴a-7=0,b-2=0,
解得:a=7,b=2,
由三角形三边关系定理得:7-2<c<7+2,即5<c<9,
又∵c为奇数,
∴c=7,
∴△ABC的周长为7+2+7=16.
故答案为:16.
3.一个三角形的两边长为2和6,第三边为偶数,则这个三角形的周长为_______
【答案】14
【解析】根据在三角形中任意两边之和大于第三边,任意两边之差小于第三边.即可求解.
解:第三边的取值范围是大于4且小于8,又第三边是偶数,
故第三边是6.
∴该三角形的周长是:2+6+6=14.
故答案为:14.
【点睛】首先根据三角形的三边关系确定第三边的取值范围,再根据第三边是偶数确定第三边的长.
4.已知三角形的三边长分别为5、a、10,则a的取值范围是 _____;如果这个三角形中有两条边相等,那么它的周长为 _____.
【答案】(1)5<a<15;(2)25;
【解析】根据三角形的三边关系可得8-4<a<8+4,再解即可得到a的取值范围;根据三角形的三边关系结合已知条件可得a=8,然后求周长即可.
解:根据三角形的三边关系可得:
10-5<a<10+5,
即5<a<15,
∵这个三角形中有两条边相等,
∴a=10或a=5(不符合三角形的三边关系,不合题意,舍去)
∴周长为5+10+10=25,
故答案为:5<a<15;25.
类型三、利用三角形三边关系求等腰三角形周长
例3-1.已知等腰三角形两边的长分别为3和7,则此等腰三角形的周长为( )
A. 13 B. 17 C. 13或17 D. 13或10
【答案】B
【解析】等腰三角形两边的长为3和7,具体哪条是底边,哪条是腰没有明确说明,因此要分两种情况讨论.
解:①当腰是3,底边是7时,3+3<7不满足三角形的三边关系,因此舍去.
②当底边是3,腰长是7时,7+7>3能构成三角形,则其周长=3+7+7=17.
故选:B.
【点睛】本题考查了等腰三角形的性质和三角形的三边关系,解题时注意:若没有明确腰和底边,则一定要分类进行讨论,还应验证各种情况是否能构成三角形,这是解题的关键.
针对训练3
1 .等腰三角形的一条边长为2cm,另一条边长为5cm,则它的周长是__________cm.
答案:12
解析:①当2cm为底时, 其它两边都为5cm,2cm,5cm,5cm可以构成三角形,
周长为12cm;
②当2cm为腰时,
其它两边为2cm和5cm,
不能构成三角形,故舍去,
故答案为:12.
若等腰三角形的一边等于5,边等于12,则它的周长是( )
A.22 B.29 C.22或29 D.17
答案:B
解析:若5为底边长,12为腰长,
,
能组成三角形,此时它的周长是:;
若12为底边长,5为腰长,
,
不能组成三角形,故舍去.
它的周长是29.
故选:B.
3.已知等腰三角形的两边长是4和8,则这个三角形的周长是 _____.
【答案】20
【解析】分两种情况:当等腰三角形的腰长为4,底边长为8时;当等腰三角形的腰长为8,底边长为4时;然后分别进行计算即可解答.
解:分两种情况:
当等腰三角形的腰长为4,底边长为8时,
∵4+4=8,
∴不能组成三角形;
当等腰三角形的腰长为8,底边长为4时,
∴等腰三角形的周长=8+8+4=20;
综上所述:这个三角形的周长是20,
故答案为:20.
4.若等腰三角形的两条边a,b满足,则等腰三角形的周长为______.
【答案】4+或2+
【解析】根据二次根式有意义,可得a=2,代入求得b=,利用三边关系求周长即可.
解:由题意,得3a-6≥0,2-a≥0
∴a=2
将a=2代入,得b=
当腰为2时,符合三角形三边关系,周长为4+
当腰为时,符合三角形三边关系,周长为2+
故答案为:4+或2+
【点睛】本题主要考查二次根式有意义的条件,以及三角形三边关系求周长的问题,利用二次根式有意义的条件得出a值是解题关键.
类型四、利用三角形三边关系求等腰三角形一边的长
例4-1.等腰三角形的周长为20cm,一边为8cm,则腰长为( )
A. 4cm B. 8cm C. 4cm或8cm D. 6cm或8cm
【答案】D
【解析】分8cm是等腰三角形的腰长与底边长两种情况进行讨论.
解:∵等腰三角形的周长为20cm,
∴当8cm是腰长时,底边=20-8-8=4cm;
∴当8cm是底边长时,腰长==6cm,
∴腰长为8cm或6cm,
故选:D.
针对训练4
1.等腰三角形的周长为20cm,一边长为6cm,则底边长为_____cm.
【答案】6或8
【解析】分6cm是底边与腰长两种情况讨论求解.
解:①6cm是底边时,腰长=(20-6)=7cm,
此时三角形的三边分别为7cm、7cm、6cm,
能组成三角形,
②6cm是腰长时,底边=20-6×2=8cm,
此时三角形的三边分别为6cm、6cm、8cm,
能组成三角形,
综上所述,底边长为6或8cm.
故答案为:6或8.
一个等腰三角形的两边长分别为3cm,6cm,则它的腰长是( )
A.3cm B.6cm C.3cm或6cm D.5cm
答案:B
解析:分两种情况考虑:
若3cm为等腰三角形的腰长,则三边分别为3cm,3cm,6cm,,不符合题意,舍去;
若6cm为等腰三角形的腰长,则三边分别为6cm,6cm,3cm,符合题意,
则它的腰长是6cm.
故选:B.
类型五、利用三角形三边关系判定三角形的形状
例5-1.已知a,b,c是△ABC的三边长,满足|a-7|+(b-2)2=0,c为奇数,判断三角形的形状,并求出△ABC的周长.
【答案】 等腰三角形,16
【解析】根据在三角形中任意两边之和>第三边,任意两边之差<第三边;可求第三边长的范围,再根据奇数的定义得出答案.
解:∵|a-7|+(b-2)2=0,
∴a-7=0,b-2=0,
解得:a=7,b=2,
由三角形三边关系定理得:7-2<c<7+2,即5<c<9,
又∵c为奇数,
∴c=7,
所以△ABC是等腰三角形
∴△ABC的周长为7+2+7=16.
故答案为:等腰三角形,16.
针对训练5
1.一个三角形的两边长为2和6,第三边为偶数,判断三角形的形状,并求出这个三角形的周长。
【答案】 等腰三角形 14
【解析】根据在三角形中任意两边之和大于第三边,任意两边之差小于第三边.即可求解.
解:第三边的取值范围是大于4且小于8,又第三边是偶数,
故第三边是6.
所以该三角形是等腰三角形
∴该三角形的周长是:2+6+6=14.
故答案为:等腰三角形 14.
【点睛】首先根据三角形的三边关系确定第三边的取值范围,再根据第三边是偶数确定第三边的长.
2.已知a,b,c是△ABC的三边长,a,b满足|a-7|+(b-1)2=0,c为奇数,判断三角形的形状.
【答案】等腰三角形
【解析】根据非负数的性质列式求出a、b的值,再根据三角形的任意两边之和大于第三边,两边之差小于第三边求出c的取值范围,再根据c是奇数求出c的值.
解:∵a,b满足|a-7|+(b-1)2=0,
∴a-7=0,b-1=0,
解得a=7,b=1,
∵7-1=6,7+1=8,
∴6<c<8,
又∵c为奇数,
∴c=7,
所以三角形是等腰三角形
3.已知a,b是等腰三角形ABC的两边长,且a、b满足a2+b2+29=10a+4b,|c|=5判断这个等腰三角形的形状.
【答案】等腰三角形
【解析】利用配方法分别求出a、b,根据三角形三边关系判断
解:a2+b2+29=10a+4b,
a2-10a+25+b2-4b+4=0,
(a-5)2+(b-2)2=0,
a-5=0,b-2=0,
解得,a=5,b=2,
|c|=5
C=5
∴这个三角形是等腰三角形
类型六、利用三角形三边关系结合中线求等腰三角形三边
例6-1.等腰三角形一腰上的中线把它的周长分为21cm和15cm的两部分,这个等腰三角形的腰长为 _____.
【答案】14cm或10cm
【解析】根据题意可知腰与底的差为6,结合等腰三角形的周长为36,可求得腰长.
解:设腰长为x cm,底为y cm,
根据题意可知x-y=21-15=6(cm)或y-x=6(cm),
且x+x+y=36,
当x-y=6时,可解得x=14,此时三角形的三边为14、14、8,满足三角形的三边关系;
当y-x=6时,可解得x=10,此时三角形的三边为10、10、16,满足三角形的三边关系;
综上可知,三角形的腰长为14cm或10cm.
故答案为:14cm或10cm.
针对训练6
1.在△ABC中,AB=BC,中线AD将这个三角形的周长分成15和12两部分,则AC的长为( )
A.7 B.11 C.7或11 D.8或10
【答案】C
【分析】设AB=BC=2x,AC=y,则BD=CD=x,根据周长分成两部分可得分两种情况讨论即可,注意三角形三边关系的应用.
解:设AB=BC=2x,AC=y,
∵AD为BC边上的中线,
∴则BD=CD=x,
∵中线AD将这个三角形的周长分成15和12两部分,
∴当AB+BD=15,且AC+CD=12时,
则2x+x=15,且y+x=12,
由2x+x=15解得:x=5,
∴y+5=12,
解得:y=7,
∴三边长分别为10,10,7(符合题意),
∴AC=7;
当AB+BD=12,且AC+CD=15时,
则2x+x=12,且y+x=15,
由2x+x=12解得:x=4,
∴y+4=15,
解得:y=11,
∴三边长分别为8,8,11(符合题意),
∴AC=11,
综上所述:AC的长为7或11,
故选:C.
【点拨】本题考查了三角形的中线以及三角形三边关系,注意要分两种情况讨论是正确解答本题的关键.
2.在等腰三角形ABC中,,一腰上的中线BD将这个三角形的周长分成15cm和6cm两部分,这个等腰三角形的三边长为__________
答案:10cm,10cm,1cm
解析:设,,则,
AC上的中线BD将这个三角形的周长分成15和6两部分,
有两种情况:
(1)当,且,
解得:,,
三边长分别为10cm,10cm,1cm;
(2)当且时,
解得:,,此时腰长为4,
根据三角形三边关系,任意两边之和大于第三边,而,
故这种情况不存在.
腰长只能是10cm.
故答案为:10cm,10cm,1cm.
类型七、利用三角形三边关系证明线段的不等关系
例7-1.如图,D为的边BC上一点,试判断与的周长之间的大小关系,并加以证明.
答案:的周长,见解析
解析:证明:在中,,
在中,,
,
即,
的周长
针对训练7
1.如图所示,由三角形两边的和大于第三边,可得到的结论是( )
A. AB+AD>BC B. PD+CD>BP C. AB+AC>BC D. BP+CP>AC
【答案】C
【解析】利用三角形的三边关系进行分析即可.
解:在△ABC中,AB+AC>BC,
故选:C.
2.如图,点P是内部的一点.
(1)通过度量线段AB,AC,PB,PC的长度,比较与的大小.
(2)改变点P的位置,上述结论还成立吗?
(3)你能说明上述结论为什么正确吗?
答案:(1).
(2)成立.
(3)见解析
解析:解:(3)延长BP交AC于点D.
在中,,①
在中,,②
①+②得,
所以.
3.如图,已知为内两点.求证:.
答案:如图,延长,分别交于点,交于点.
在中,.
在中,.
在中,.
,
.
又,
.
类型八、利用三角形三边关系化简含绝对值的式子
例8-1.已知一个三角形三边长为a、b、c,则|a-b-c|-|a+b-c|=( )
A. -2a+2c B. -2b+2c C. 2a D. -2c
【答案】A
【解析】根据三角形的三边关系得到b+c>a,a+b>c,根据绝对值的性质、合并同类项法则计算,得到答案.
解:∵a、b、c是一个三角形三边长,
∴b+c>a,a+b>c,
∴|a-b-c|-|a+b-c|
=-(a-b-c)-(a+b-c)
=-a+b+c-a-b+c
=-2a+2c,
故选:A.
针对训练8
1.已知a,b,c是△ABC的三条边长,化简|a+b-c|+|c-a-b|的结果为_____.
【答案】2a+2b-2c
【解析】先根据三角形的三边关系判断出a+b-c与c-b-a的符号,再去绝对值符号,合并同类项即可;
解:∵a、b、c为△ABC的三条边长,
∴a+b-c>0,c-a-b<0,
∴原式=a+b-c-(c-a-b)
=a+b-c-c+a+b
=2a+2b-2c
故答案为:2a+2b-2c.
2.已知三角形的三边长分别为a,b,c,化简:|a+b-c|-2|a-b-c|+|a+b+c|.
【解析】三角形三边满足的条件是:两边和大于第三边,两边的差小于第三边,根据此条件来确定绝对值内的式子的正负,从而化简计算即可.
解:∵△ABC的三边长分别是a、b、c,
∴必须满足两边之和大于第三边,两边的差小于第三边,则a+b-c>0,a-b-c<0,a+b+c>0,
∴|a+b-c|-2|a-b-c|+|a+b+c|=a+b-c+2a-2b-2c+a+b+c=4a-2c.
3.已知a,b,c是三角形的三边长.
(1)化简:|a-b-c|+|b-c-a|+|c-a-b|;
(2)若a=10,b=8,c=6,求(1)中式子的值.
【解析】(1)根据三角形的三边关系,两边之和大于第三边,即可确定绝对值符号内的式子的符号,从而去掉绝对值符号,然后进行化简即可;
(2)代人a=10,b=8,c=6求值即可.
解:(1)∵a,b,c是三角形的三边长,
∴b+c>a,c+a>b,a+b>c,
∴a-b-c<0,b-c-a<0,c-a-b<0,
∴|a-b-c|+|b-c-a|+|c-a-b|=b+c-a+c+a-b+a+b-c=a+b+c.
(2)把a=10,b=8,c=6代入(1)中式子,得原式=10+8+6=24.
巩固练习
1.某等腰三角形的三边长分别为x,3,,则该三角形的周长为( )
A.11 B.11或8 C.11或8或5 D.与x的取值有关
答案:B
解析:当时,此时,,能组成三角形,此时三角形的周长为.当时,此时,,不能组成三角形.当时,此时,,能组成三角形,此时三角形的周长为.
2.已知三角形的三边长分别为3、4、x,则x不可能是( )
A.4 B.5 C.6 D.7
答案:D
解析:,,
.
观察四个选项,x不可能是7.
故选:D.
3.等腰三角形的周长为13cm,其中一边长为3cm,则该等腰三角形的底边长为( )
A.7cm B.3cm C.9cm D.5cm
答案:B
解析:当长是3cm的边是底边时,
三边为3cm,5cm,5cm,等腰三角形成立;
当长是3cm的边是腰时,底边长是:,
而,不满足三角形的三边关系;
故底边长是:3cm.
故选:B.
4.已知a、b、c是的三条边长,化简的结果为( )
A. B. C. D.0
答案:D
解析:a、b、c为的三条边长,
,,
原式.
故选:D.
5.三角形的两边长分别是10和8,则第三边的x取值范围是_____.
答案:
解析:根据三角形的三边关系:,
解得:.
故答案为:.
6.已知a,b,c是的三边长,b,c满足,且a为方程的解,则的周长为___________.
答案:7
解析:因为,所以,,解得,.因为a为方程的解,所以,解得或2.因为a,b,c为的三边长,所以,所以,所以的周长为.
故答案为7.
7.若等腰三角形的两边长分别为6cm和8cm,则它的周长是________.
答案:或
解析:等腰三角形的两条腰相等
①当腰为6cm时:三角形的周长为:;
②当腰为8cm时:三角形的周长为:;
故答案为:或.
8.已知等腰三角形的周长为20,其中一边的长为6,则底边的长为_________.
答案:6或8
解析:设底边长为x,腰长为y,
则,
①当腰长时,
,
;
三边长分别为6,6,8能构成三角形,符合题意;
故;
②当底边长时,
,
;
三边长分别为7,7,6能构成三角形,符合题意;
故;
综上所述,或;
故答案为:6或8.
9.如图,由三角形两边的和大于第三边,得
___________,①
___________.②
将不等式①,②的左边、右边分别相加,得_________,③
不等式③两边都减PD,得.
答案:;;
解析:由三角形两边的和大于第三边,得,.将不等式左边、右边分别相加,得,即.
10.已知的三边长分别为a,b,c.
(1)若a,b,c满足,试判断的形状;
(2)若,,且c为整数,求的周长的最大值及最小值.
答案:(1),
,,,
是等边三角形.
(2),,,即,又c为整数,
,5,6,
当时,的周长最小,最小值;
当时,的周长最大,最大值.
11.等腰三角形一腰上的中线把该三角形的周长分为13.5 cm和11.5 cm两部分,求这个等腰三角形各边的长.
答案:设在中,,BD是AC边上的中线,
依题意,当时,,,
所以,
解得.
当时,,
.所以,
解得.
综上,这个等腰三角形三边的长分别为9cm,9cm,7cm或.
12.已知的三边长分别为a,b,c,化简.
答案:
解析:a,b,c是的三边长,
,,
.
13.等腰三角形的三边长分别为,,7,求等腰三角形的周长.
答案:三角形的周长为19.5或23
解析:①当是底边时,则腰长为:,7,
,
,
,
等腰三角形的周长;
②当是底边时,则腰长为:,7,
,
,
,
等腰三角形的周长;
③当7是底边时,则腰长为:,,
,
,
,,
,
不能构成三角形.
则三角形的周长为19.5或23.
14.如图,四边形ABCD,试说明.
答案:如图,延长BD交AC于点E.
因为,
所以.
因为,
所以.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
