北师大版六年级下册 神奇的莫比乌斯带 课件(共24张PPT)
文档属性
| 名称 | 北师大版六年级下册 神奇的莫比乌斯带 课件(共24张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 10.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-17 21:11:15 | ||
图片预览





文档简介
(共24张PPT)
1.准备宽4cm、长在20cm—30cm的纸条6条。
(其中二等分2条,三等分1条。)
2.双面胶1个。
3.安全剪刀1把
4.彩笔2支
例如二等分:
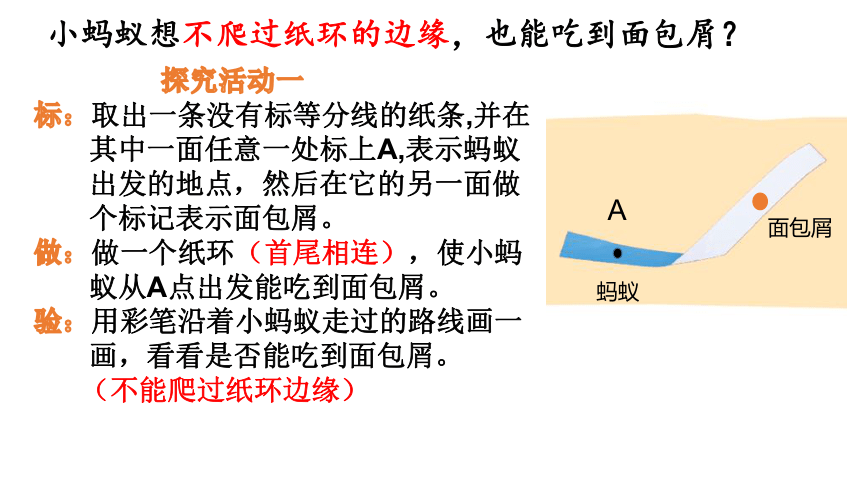
小蚂蚁想不爬过纸环的边缘,也能吃到面包屑?
A
面包屑
蚂蚁
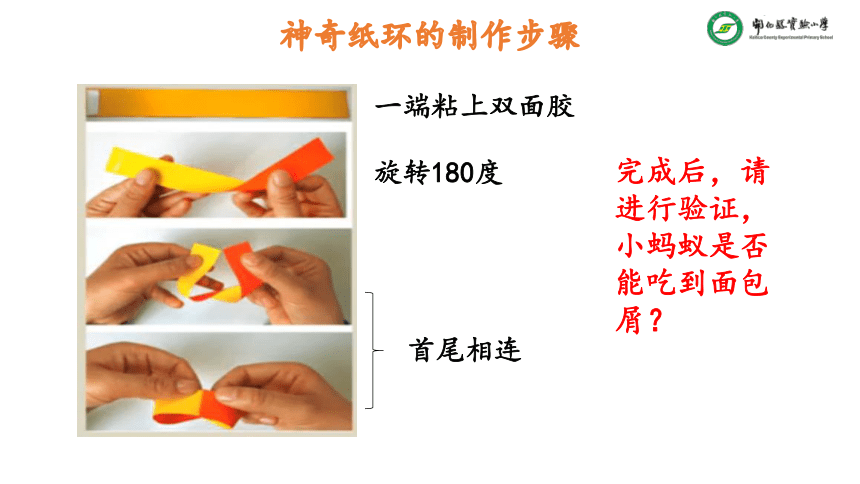
一端粘上双面胶
旋转180度
首尾相连
完成后,请进行验证,小蚂蚁是否能吃到面包屑?
小蚂蚁在这个神奇的纸环上,无论它在外面的哪个位置,都不必爬过边缘就能吃到面包屑。 因为这个神奇的纸环,把小蚂蚁和面包屑连在了同一条线上。
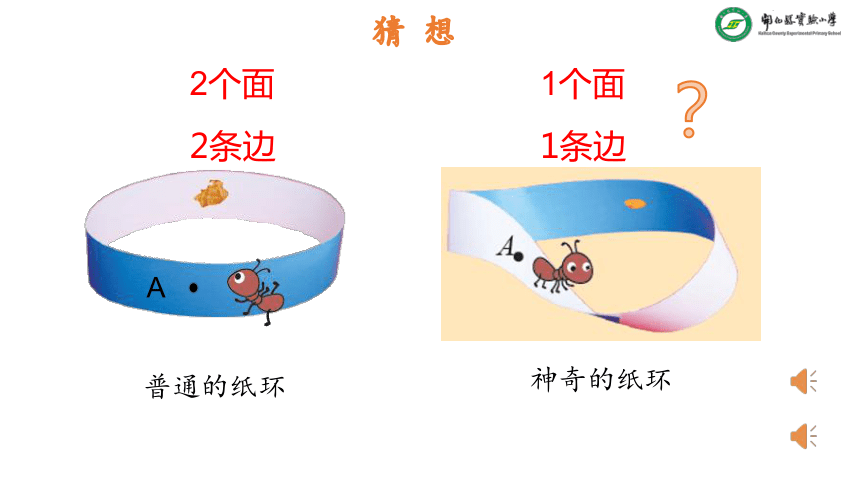
探究神奇的纸环的奥秘?
A
2个面
1个面
普通的纸环
神奇的纸环
2条边
1条边
←
从起点出发,
又回到起点
一
条
边
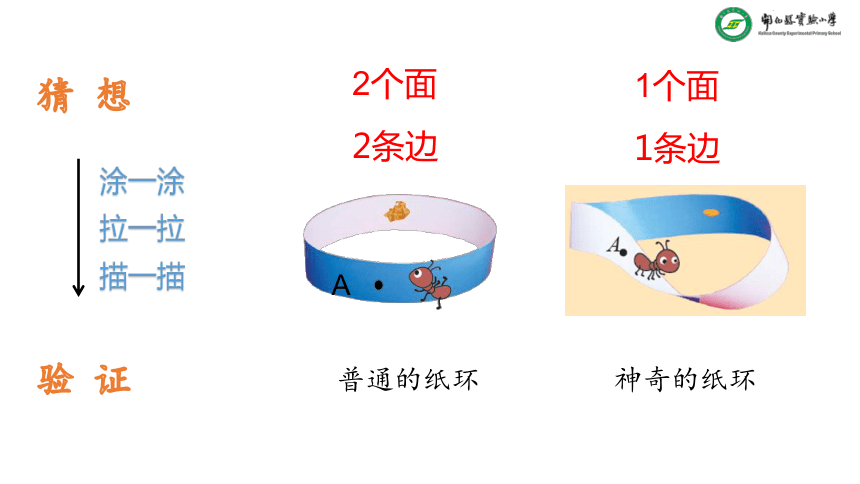
A
2个面
1个面
普通的纸环
神奇的纸环
2条边
1条边
这样的一条边、一个面的圈是德国数学家莫比乌斯在1858年研究四色定理时发现的,所以就以他的名字命名叫它“ 莫比乌斯带”,也有人叫它“莫比乌斯圈”,还有人管它叫“怪圈”。
探究莫比乌斯带沿二等分线剪开的奥秘
温馨提醒:
→
→
2个普通的纸环
1个是原来2倍的纸环
1个大圈套1个小圈
→
传送带,打印机的色带设计成莫比乌斯带,就不会只磨损一面,从而延长了使用寿命。
莫比乌斯带循环反复的几何特征,蕴含着永恒、无限的意义。可回收物标志就表示可循环使用的意思。
中国科技馆的“三叶扭结”雕塑就是莫比乌斯带,象征科学没有国界,各种科学之间相互连通。
2010年上海世博会湖南馆用莫比乌斯带来展示风土人情,突出湖南元素,体现“天人合一” “和谐自然”。
艺术的桥梁
哈萨克斯坦国家图书馆
凤凰卫视北京总部
过山车
莫比乌斯带爬梯
克莱因瓶
克莱因瓶是由德国数学家菲利克斯·克莱因提出的。克莱因瓶的结构非常简单,一个瓶子底部有一个洞,现在延长瓶子的颈部,并且扭曲地进入瓶子内部,然后和底部的洞相连接。这个物体没有“边”,它的表面不会终结。一只苍蝇可以从瓶子的内部直接飞到外部而不用穿过表面(所以说它没有内外部之分)。
克
莱
因
图形的运动
旋转180度
不改变
特点:1个面、1条边
广泛应用
一、填空
1.如右图,人行走在这样的带子上,不越过边缘,( )(填“能”或“不能”)到达带子上任意一点。
2.打印机的色带应用了莫比乌斯带,是因为这样做不会只磨损一面,就延
长了色带的使用寿命,节约了材料。我认为是( )的。(填“对”
或“不对”)
二、探究:
你能发现莫比乌斯带沿等分线剪开的奥秘吗?
二 等 分 一个大圈(不是莫比乌斯带)
三等分
四等分
五等分
我的发现:
(温馨提醒:先剪一剪,再验一验,剪后的纸环是否还是莫比乌斯带,并完成表格。)
1.准备宽4cm、长在20cm—30cm的纸条6条。
(其中二等分2条,三等分1条。)
2.双面胶1个。
3.安全剪刀1把
4.彩笔2支
例如二等分:
小蚂蚁想不爬过纸环的边缘,也能吃到面包屑?
A
面包屑
蚂蚁
一端粘上双面胶
旋转180度
首尾相连
完成后,请进行验证,小蚂蚁是否能吃到面包屑?
小蚂蚁在这个神奇的纸环上,无论它在外面的哪个位置,都不必爬过边缘就能吃到面包屑。 因为这个神奇的纸环,把小蚂蚁和面包屑连在了同一条线上。
探究神奇的纸环的奥秘?
A
2个面
1个面
普通的纸环
神奇的纸环
2条边
1条边
←
从起点出发,
又回到起点
一
条
边
A
2个面
1个面
普通的纸环
神奇的纸环
2条边
1条边
这样的一条边、一个面的圈是德国数学家莫比乌斯在1858年研究四色定理时发现的,所以就以他的名字命名叫它“ 莫比乌斯带”,也有人叫它“莫比乌斯圈”,还有人管它叫“怪圈”。
探究莫比乌斯带沿二等分线剪开的奥秘
温馨提醒:
→
→
2个普通的纸环
1个是原来2倍的纸环
1个大圈套1个小圈
→
传送带,打印机的色带设计成莫比乌斯带,就不会只磨损一面,从而延长了使用寿命。
莫比乌斯带循环反复的几何特征,蕴含着永恒、无限的意义。可回收物标志就表示可循环使用的意思。
中国科技馆的“三叶扭结”雕塑就是莫比乌斯带,象征科学没有国界,各种科学之间相互连通。
2010年上海世博会湖南馆用莫比乌斯带来展示风土人情,突出湖南元素,体现“天人合一” “和谐自然”。
艺术的桥梁
哈萨克斯坦国家图书馆
凤凰卫视北京总部
过山车
莫比乌斯带爬梯
克莱因瓶
克莱因瓶是由德国数学家菲利克斯·克莱因提出的。克莱因瓶的结构非常简单,一个瓶子底部有一个洞,现在延长瓶子的颈部,并且扭曲地进入瓶子内部,然后和底部的洞相连接。这个物体没有“边”,它的表面不会终结。一只苍蝇可以从瓶子的内部直接飞到外部而不用穿过表面(所以说它没有内外部之分)。
克
莱
因
图形的运动
旋转180度
不改变
特点:1个面、1条边
广泛应用
一、填空
1.如右图,人行走在这样的带子上,不越过边缘,( )(填“能”或“不能”)到达带子上任意一点。
2.打印机的色带应用了莫比乌斯带,是因为这样做不会只磨损一面,就延
长了色带的使用寿命,节约了材料。我认为是( )的。(填“对”
或“不对”)
二、探究:
你能发现莫比乌斯带沿等分线剪开的奥秘吗?
二 等 分 一个大圈(不是莫比乌斯带)
三等分
四等分
五等分
我的发现:
(温馨提醒:先剪一剪,再验一验,剪后的纸环是否还是莫比乌斯带,并完成表格。)
