第一章特殊平行四边形 单元测试(无答案)2023-2024学年北师大版数学九年级上册
文档属性
| 名称 | 第一章特殊平行四边形 单元测试(无答案)2023-2024学年北师大版数学九年级上册 |
|
|
| 格式 | docx | ||
| 文件大小 | 390.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-18 00:00:00 | ||
图片预览


文档简介
第一章特殊平行四边形 单元测试
一、单选题
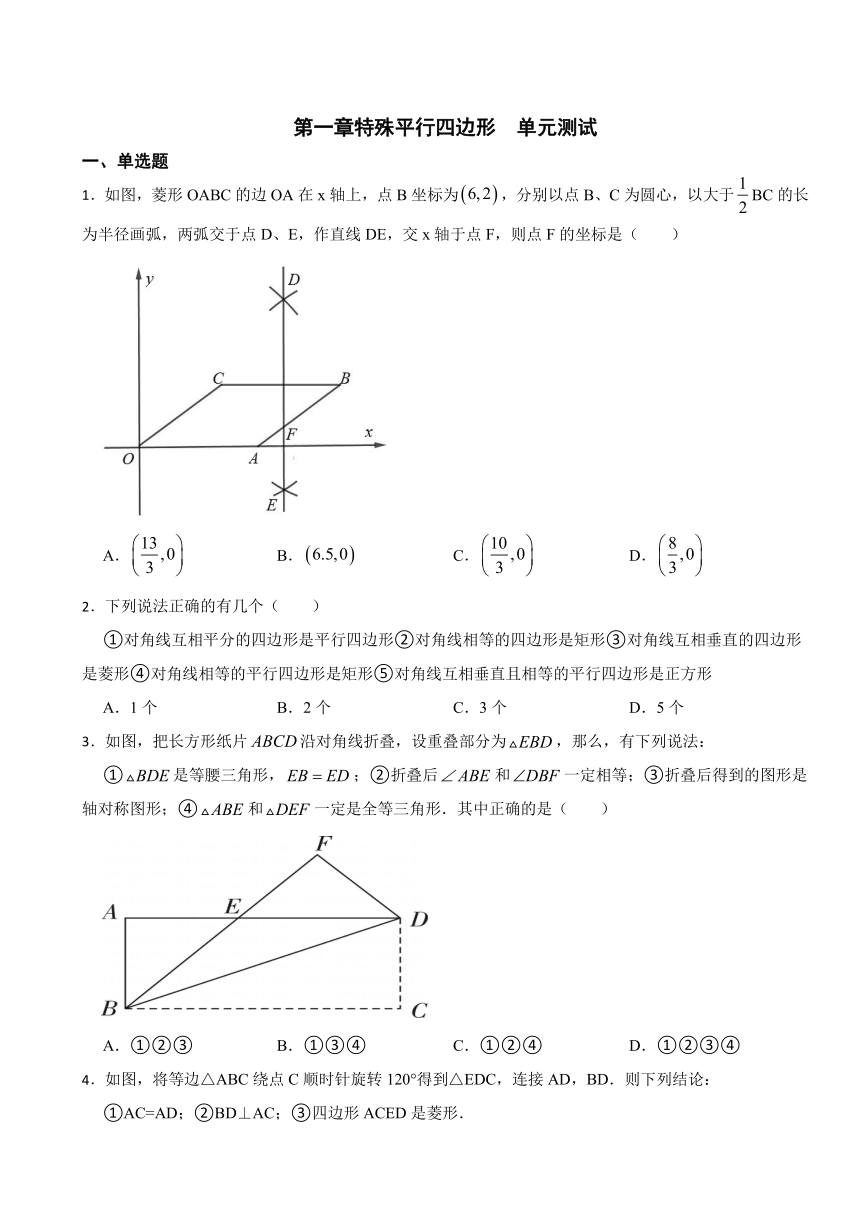
1.如图,菱形OABC的边OA在x轴上,点B坐标为,分别以点B、C为圆心,以大于BC的长为半径画弧,两弧交于点D、E,作直线DE,交x轴于点F,则点F的坐标是( )
A. B. C. D.
2.下列说法正确的有几个( )
①对角线互相平分的四边形是平行四边形②对角线相等的四边形是矩形③对角线互相垂直的四边形是菱形④对角线相等的平行四边形是矩形⑤对角线互相垂直且相等的平行四边形是正方形
A.1个 B.2个 C.3个 D.5个
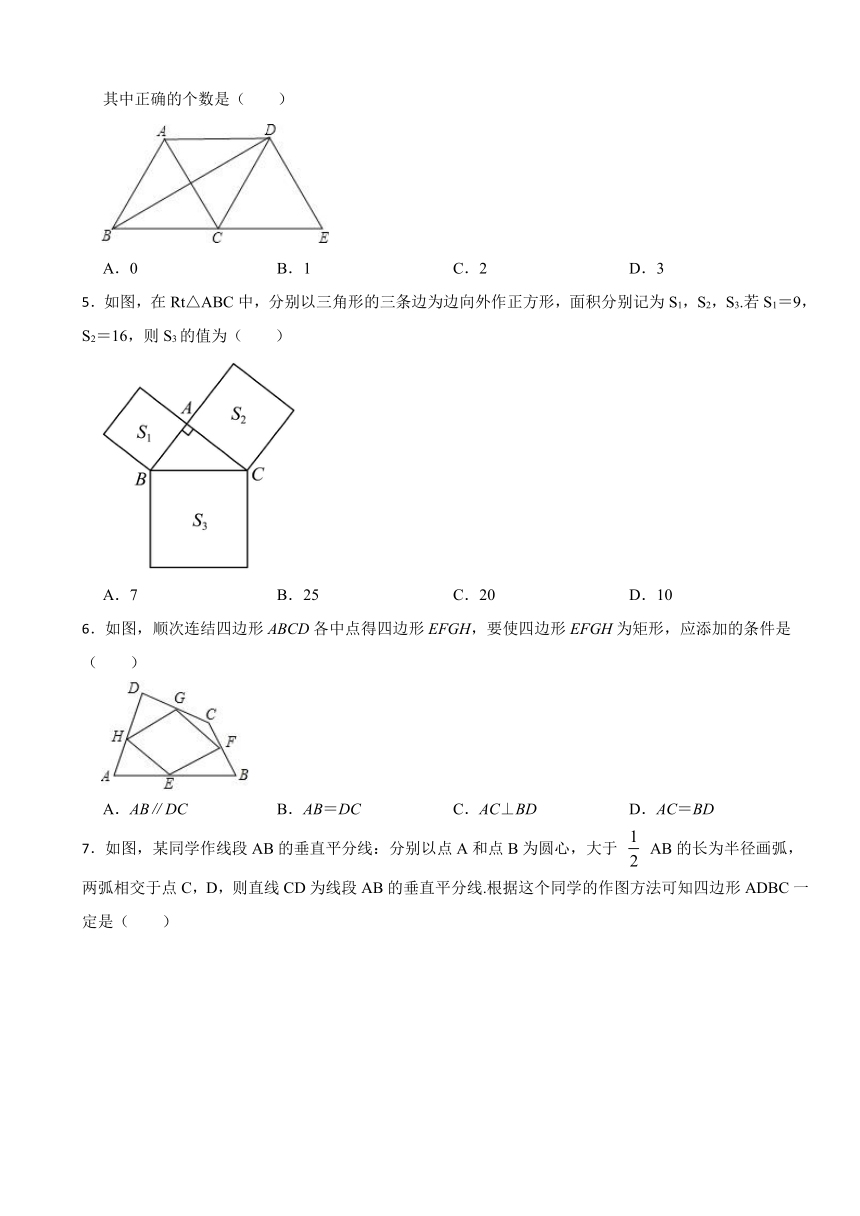
3.如图,把长方形纸片沿对角线折叠,设重叠部分为,那么,有下列说法:
①是等腰三角形,;②折叠后和一定相等;③折叠后得到的图形是轴对称图形;④和一定是全等三角形.其中正确的是( )
A.①②③ B.①③④ C.①②④ D.①②③④
4.如图,将等边△ABC绕点C顺时针旋转120°得到△EDC,连接AD,BD.则下列结论:
①AC=AD;②BD⊥AC;③四边形ACED是菱形.
其中正确的个数是( )
A.0 B.1 C.2 D.3
5.如图,在Rt△ABC中,分别以三角形的三条边为边向外作正方形,面积分别记为S1,S2,S3.若S1=9,S2=16,则S3的值为( )
A.7 B.25 C.20 D.10
6.如图,顺次连结四边形ABCD各中点得四边形EFGH,要使四边形EFGH为矩形,应添加的条件是( )
A.AB∥DC B.AB=DC C.AC⊥BD D.AC=BD
7.如图,某同学作线段AB的垂直平分线:分别以点A和点B为圆心,大于 AB的长为半径画弧,两弧相交于点C,D,则直线CD为线段AB的垂直平分线.根据这个同学的作图方法可知四边形ADBC一定是( )
A.菱形 B.平行四边形
C.矩形 D.一般的四边形
8.如图,点E是矩形的边上的中点,将折叠得到,点F在矩形内部,的延长线交于点G,若,,则的长为( )
A.7 B.8 C.9 D.10
9.如图,已知正方形的边长为,为边上一点,,为边上一点,沿将折叠,使得点的对应点为,连接,,,,有以下结论:①若,则②若,则③的面积最大值是④的最小值是,其中正确的有( )
A.① ② ③ ④ B.① ③ ④ C.① ② ④ D.① ② ③
10.如图,矩形纸片 ,点M、N分别在矩形的边 、 上,将矩形纸片沿直线 折叠,使点C落在矩形的边 上,记为点P,点D落在G处,连接 ,交 于点Q,连接 .下列结论:①四边形 是菱形;②点P与点A重合时, ;③ 的面积S的取值范围是 .其中所有正确结论的序号是( )
A.①②③ B.①② C.①③ D.②③
二、填空题
11.在菱形ABCD中,对角线AC=30,BD=60,则菱形ABCD的面积为 .
12.在矩形ABCD中,点E为AD的中点,点F是BC上的一点,连接EF和DF,若AB=4,BC=8,EF=2 ,则DF的长为 .
13.如图,正方形ABCD的边长为4cm,点E,F分别是BC,CD的中点,连结BF,DE,则图中阴影部分的面积是 cm2.
14.如图,在正方形中,,点E是边上的点,且,点F是对角线所在直线上一点且.过点F作,边交直线于点G,则的长为 .
15. 菱形ABCD,点A,B,C,D均在坐标轴上. ∠ABC=120°,点A(-6,0),点E是CD的中点,点P是OC上的一动点,则△PDE周长的最小值是 .
三、解答题
16.如图,在菱形中,,求菱形的周长.
17.如图,将矩形ABCD沿对角线AC折叠,点B的对应点为E,AE与CD相交于点F.
(1)求证:△DAF≌△ECF.
(2)若∠FCE=40°,求∠CAB的度数.
18.如图,在矩形ABCD中,连接对角线AC,分别过点B、点D作AC的垂线交于点E、F.证明:AF=CE.
19. 如图,将一张矩形纸片沿直线折叠,使点落在点处,点落在点处,直线交于点,交于点.
(1)请写出图中一对全等的三角形;
(2)若,,求折痕的长.
20.已知:如图,在△ABC中,AB=AC,点D为BC中点,AN是△ABC外角∠CAM的平分线,CE⊥AN,垂足为点E.求证:四边形ADCE为矩形.
21.已知:矩形ABCD中,AB=10,AD=8,点E是BC边上一个动点,将△ABE沿AE折叠得到△AB′E。
(1)如图1,点G和点H分别是AD和AB′的中点,若点B′在边DC上。
①求GH的长;
②求证:△AGH≌△B′CE;
(2)如图2,若点F是AE的中点,连接B′F,B′F∥AD,交DC于I。
①求证:四边形BEB′F是菱形;
②求B′F的长。
22.综合运用
如图1,点E是矩形的边上一点,连接,把沿折叠得到,点在矩形的内部,延长交射线于点F,连接,已知.
(1)当E是的中点时,求.
(2)如图2,当时,与相交于点G,求的长;
(3)如图3,当时,求的面积.
23.在平面直角坐标系中,O为原点,点A(6,0),点B在y轴的正半轴上,∠ABO=30°.矩形CODE的顶点D,E,C分别在OA,AB,OB上,OD=2.
(Ⅰ)如图①,求点E的坐标;
(Ⅱ)将矩形CODE沿x轴向右平移,得到矩形C′O′D′E′,点C,O,D,E的对应点分别为C′,O′,D′,E′.设OO′=t,矩形C′O′D′E′与△ABO重叠部分的面积为S.
①如图②,当矩形C′O′D′E′与△ABO重叠部分为五边形时,C′E′,E′D′分别与AB相交于点M,F,试用含有t的式子表示S,并直接写出t的取值范围;
②当 ≤S≤5 时,求t的取值范围(直接写出结果即可).
一、单选题
1.如图,菱形OABC的边OA在x轴上,点B坐标为,分别以点B、C为圆心,以大于BC的长为半径画弧,两弧交于点D、E,作直线DE,交x轴于点F,则点F的坐标是( )
A. B. C. D.
2.下列说法正确的有几个( )
①对角线互相平分的四边形是平行四边形②对角线相等的四边形是矩形③对角线互相垂直的四边形是菱形④对角线相等的平行四边形是矩形⑤对角线互相垂直且相等的平行四边形是正方形
A.1个 B.2个 C.3个 D.5个
3.如图,把长方形纸片沿对角线折叠,设重叠部分为,那么,有下列说法:
①是等腰三角形,;②折叠后和一定相等;③折叠后得到的图形是轴对称图形;④和一定是全等三角形.其中正确的是( )
A.①②③ B.①③④ C.①②④ D.①②③④
4.如图,将等边△ABC绕点C顺时针旋转120°得到△EDC,连接AD,BD.则下列结论:
①AC=AD;②BD⊥AC;③四边形ACED是菱形.
其中正确的个数是( )
A.0 B.1 C.2 D.3
5.如图,在Rt△ABC中,分别以三角形的三条边为边向外作正方形,面积分别记为S1,S2,S3.若S1=9,S2=16,则S3的值为( )
A.7 B.25 C.20 D.10
6.如图,顺次连结四边形ABCD各中点得四边形EFGH,要使四边形EFGH为矩形,应添加的条件是( )
A.AB∥DC B.AB=DC C.AC⊥BD D.AC=BD
7.如图,某同学作线段AB的垂直平分线:分别以点A和点B为圆心,大于 AB的长为半径画弧,两弧相交于点C,D,则直线CD为线段AB的垂直平分线.根据这个同学的作图方法可知四边形ADBC一定是( )
A.菱形 B.平行四边形
C.矩形 D.一般的四边形
8.如图,点E是矩形的边上的中点,将折叠得到,点F在矩形内部,的延长线交于点G,若,,则的长为( )
A.7 B.8 C.9 D.10
9.如图,已知正方形的边长为,为边上一点,,为边上一点,沿将折叠,使得点的对应点为,连接,,,,有以下结论:①若,则②若,则③的面积最大值是④的最小值是,其中正确的有( )
A.① ② ③ ④ B.① ③ ④ C.① ② ④ D.① ② ③
10.如图,矩形纸片 ,点M、N分别在矩形的边 、 上,将矩形纸片沿直线 折叠,使点C落在矩形的边 上,记为点P,点D落在G处,连接 ,交 于点Q,连接 .下列结论:①四边形 是菱形;②点P与点A重合时, ;③ 的面积S的取值范围是 .其中所有正确结论的序号是( )
A.①②③ B.①② C.①③ D.②③
二、填空题
11.在菱形ABCD中,对角线AC=30,BD=60,则菱形ABCD的面积为 .
12.在矩形ABCD中,点E为AD的中点,点F是BC上的一点,连接EF和DF,若AB=4,BC=8,EF=2 ,则DF的长为 .
13.如图,正方形ABCD的边长为4cm,点E,F分别是BC,CD的中点,连结BF,DE,则图中阴影部分的面积是 cm2.
14.如图,在正方形中,,点E是边上的点,且,点F是对角线所在直线上一点且.过点F作,边交直线于点G,则的长为 .
15. 菱形ABCD,点A,B,C,D均在坐标轴上. ∠ABC=120°,点A(-6,0),点E是CD的中点,点P是OC上的一动点,则△PDE周长的最小值是 .
三、解答题
16.如图,在菱形中,,求菱形的周长.
17.如图,将矩形ABCD沿对角线AC折叠,点B的对应点为E,AE与CD相交于点F.
(1)求证:△DAF≌△ECF.
(2)若∠FCE=40°,求∠CAB的度数.
18.如图,在矩形ABCD中,连接对角线AC,分别过点B、点D作AC的垂线交于点E、F.证明:AF=CE.
19. 如图,将一张矩形纸片沿直线折叠,使点落在点处,点落在点处,直线交于点,交于点.
(1)请写出图中一对全等的三角形;
(2)若,,求折痕的长.
20.已知:如图,在△ABC中,AB=AC,点D为BC中点,AN是△ABC外角∠CAM的平分线,CE⊥AN,垂足为点E.求证:四边形ADCE为矩形.
21.已知:矩形ABCD中,AB=10,AD=8,点E是BC边上一个动点,将△ABE沿AE折叠得到△AB′E。
(1)如图1,点G和点H分别是AD和AB′的中点,若点B′在边DC上。
①求GH的长;
②求证:△AGH≌△B′CE;
(2)如图2,若点F是AE的中点,连接B′F,B′F∥AD,交DC于I。
①求证:四边形BEB′F是菱形;
②求B′F的长。
22.综合运用
如图1,点E是矩形的边上一点,连接,把沿折叠得到,点在矩形的内部,延长交射线于点F,连接,已知.
(1)当E是的中点时,求.
(2)如图2,当时,与相交于点G,求的长;
(3)如图3,当时,求的面积.
23.在平面直角坐标系中,O为原点,点A(6,0),点B在y轴的正半轴上,∠ABO=30°.矩形CODE的顶点D,E,C分别在OA,AB,OB上,OD=2.
(Ⅰ)如图①,求点E的坐标;
(Ⅱ)将矩形CODE沿x轴向右平移,得到矩形C′O′D′E′,点C,O,D,E的对应点分别为C′,O′,D′,E′.设OO′=t,矩形C′O′D′E′与△ABO重叠部分的面积为S.
①如图②,当矩形C′O′D′E′与△ABO重叠部分为五边形时,C′E′,E′D′分别与AB相交于点M,F,试用含有t的式子表示S,并直接写出t的取值范围;
②当 ≤S≤5 时,求t的取值范围(直接写出结果即可).
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
