2.2.2平行四边形的判定课件(2课时)
文档属性
| 名称 | 2.2.2平行四边形的判定课件(2课时) |

|
|
| 格式 | zip | ||
| 文件大小 | 771.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-01-12 00:00:00 | ||
图片预览


文档简介
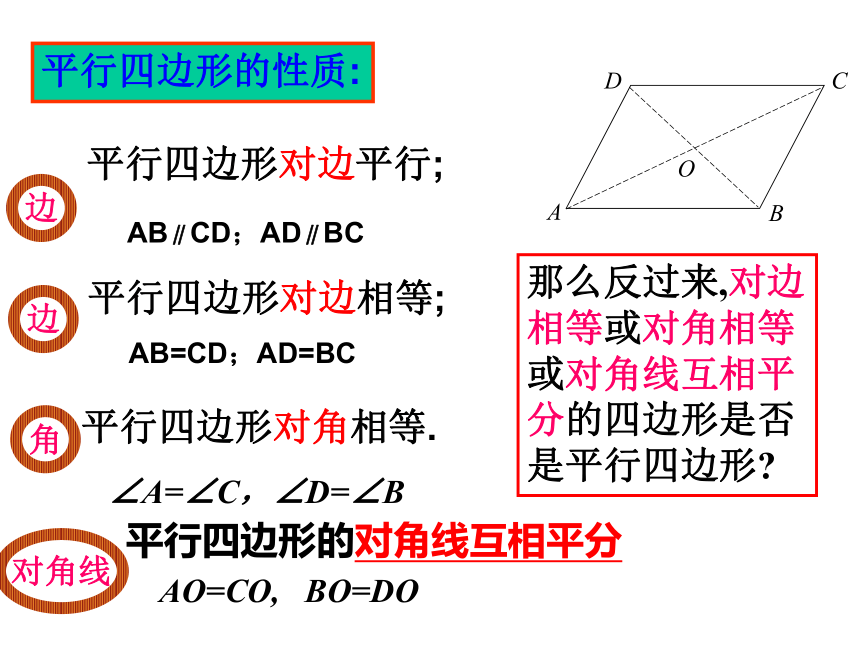
课件32张PPT。2.2.2平行四边形的判定(1)平行四边形对边相等;平行四边形对角相等.平行四边形的性质:平行四边形对边平行;AB∥CD;AD∥BCAB=CD;AD=BC∠A=∠C,∠D=∠B平行四边形的对角线互相平分AO=CO, BO=DO那么反过来,对边
相等或对角相等
或对角线互相平
分的四边形是否
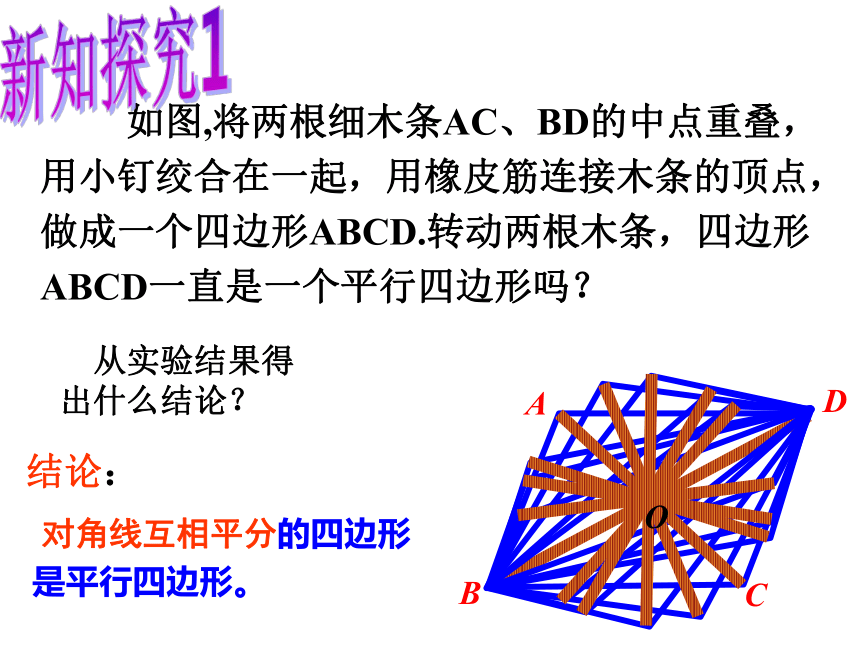
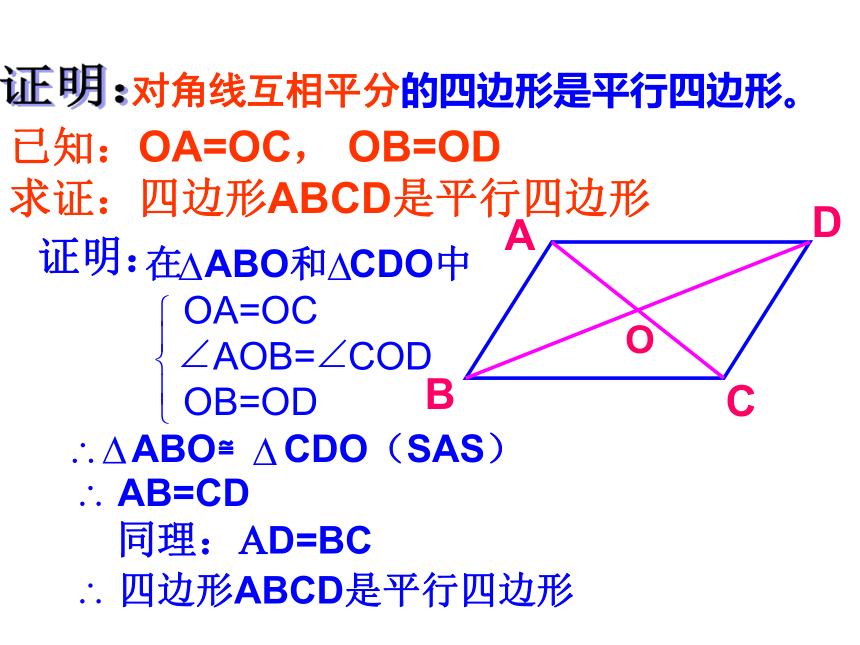
是平行四边形?边边角对角线 如图,将两根细木条AC、BD的中点重叠,用小钉绞合在一起,用橡皮筋连接木条的顶点,做成一个四边形ABCD.转动两根木条,四边形ABCD一直是一个平行四边形吗?新知探究1 从实验结果得出什么结论?BDOAC 对角线互相平分的四边形是平行四边形。结论:O已知:OA=OC, OB=OD
求证:四边形ABCD是平行四边形CA证明:在 ABO和 CDO中OA=OC
AOB= COD
OB=OD
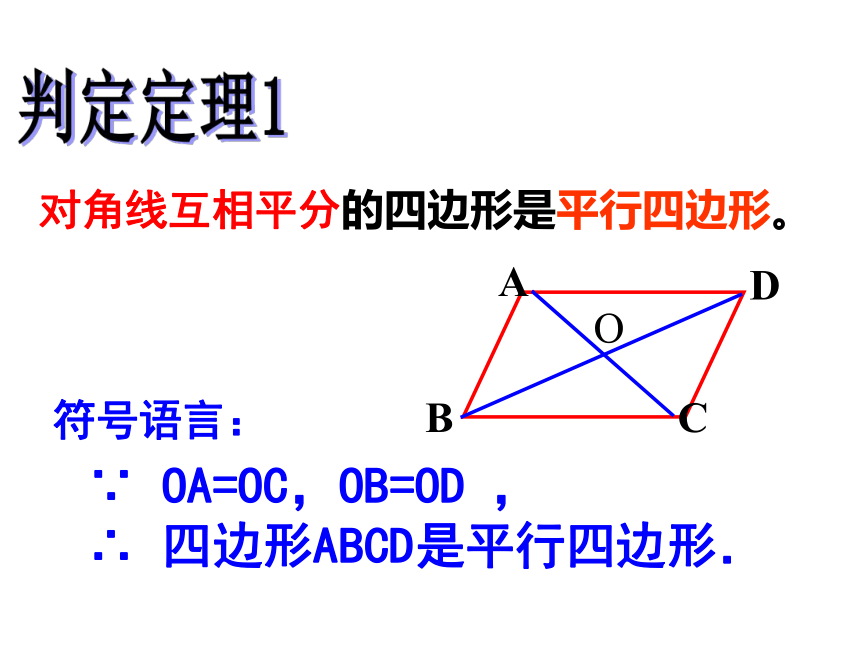
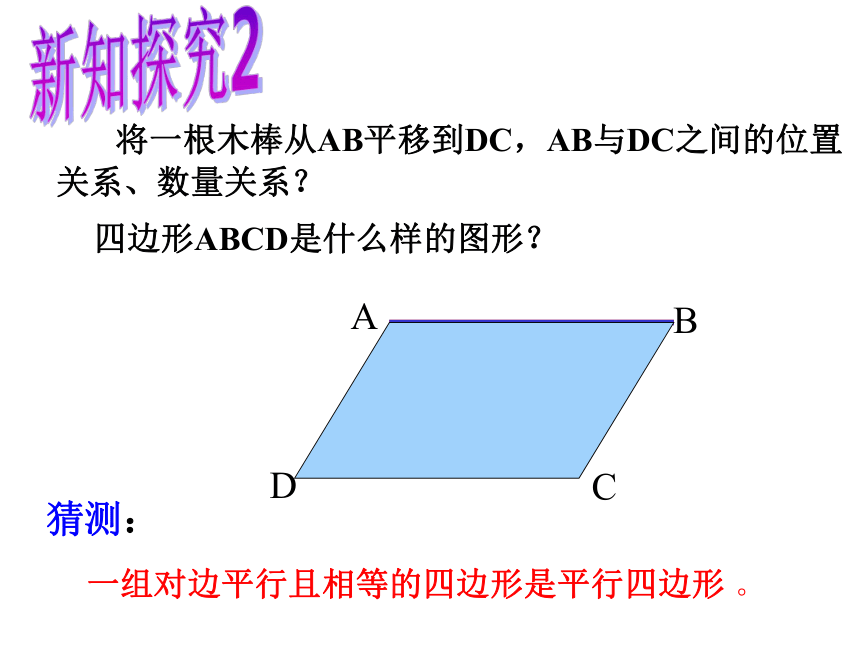
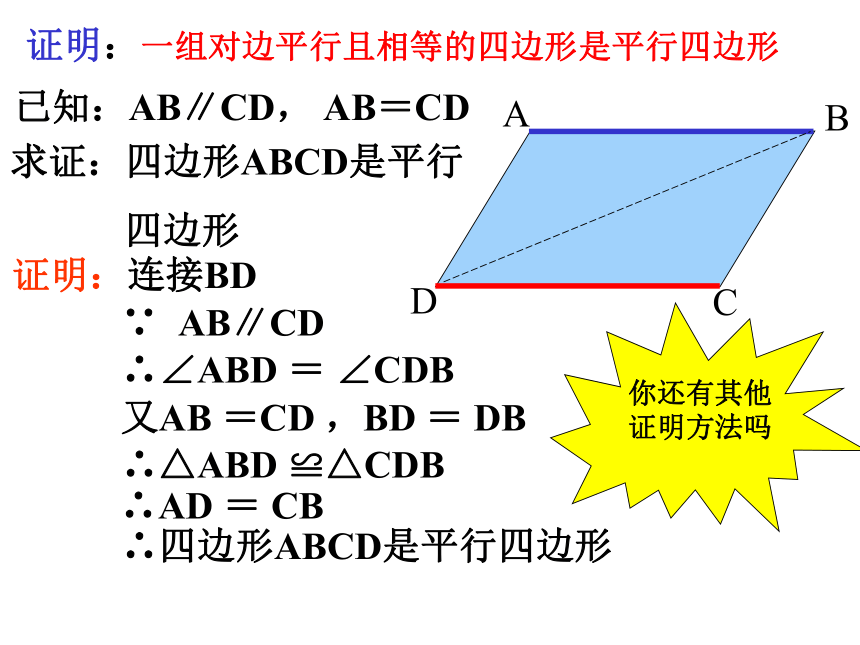
ABO≌ CDO(SAS) AB=CD同理:AD=BC 四边形ABCD是平行四边形证明: 对角线互相平分的四边形是平行四边形。对角线互相平分的四边形是平行四边形。判定定理1四边形ABCD是什么样的图形?猜测: 将一根木棒从AB平移到DC,AB与DC之间的位置关系、数量关系?新知探究2一组对边平行且相等的四边形是平行四边形 。证明:一组对边平行且相等的四边形是平行四边形已知:AB∥CD, AB=CD求证:四边形ABCD是平行
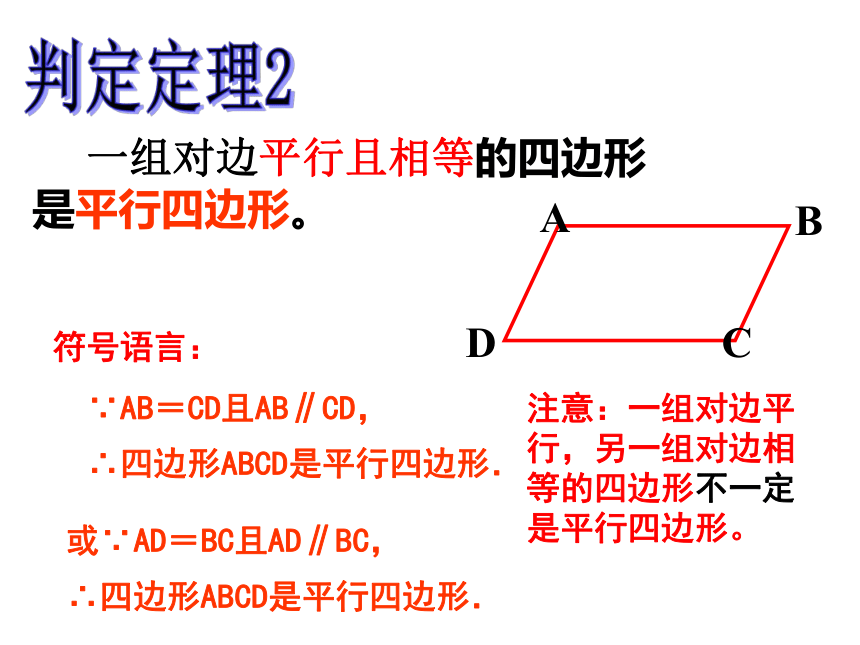
四边形证明:连接BD 一组对边平行且相等的四边形是平行四边形。判定定理2∵AB=CD且AB∥CD,
∴四边形ABCD是平行四边形. 符号语言:或∵AD=BC且AD∥BC,
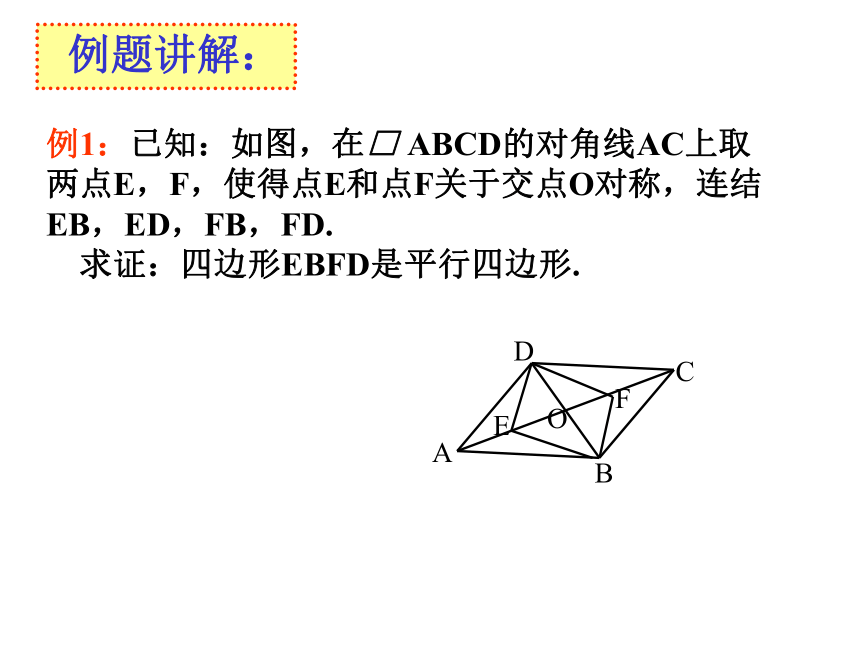
∴四边形ABCD是平行四边形. 注意:一组对边平行,另一组对边相等的四边形不一定是平行四边形。 平行四边形的判定方法1.定义法: 两组对边分别平行的四边形是平行四边形。2.判定定理1:对角线互相平分的四边形是平行四边形。3.判定定理2: 一组对边平行且相等的四边形是平行四边形。 例题讲解:例1:已知:如图,在□ ABCD的对角线AC上取
两点E,F,使得点E和点F关于交点O对称,连结
EB,ED,FB,FD.
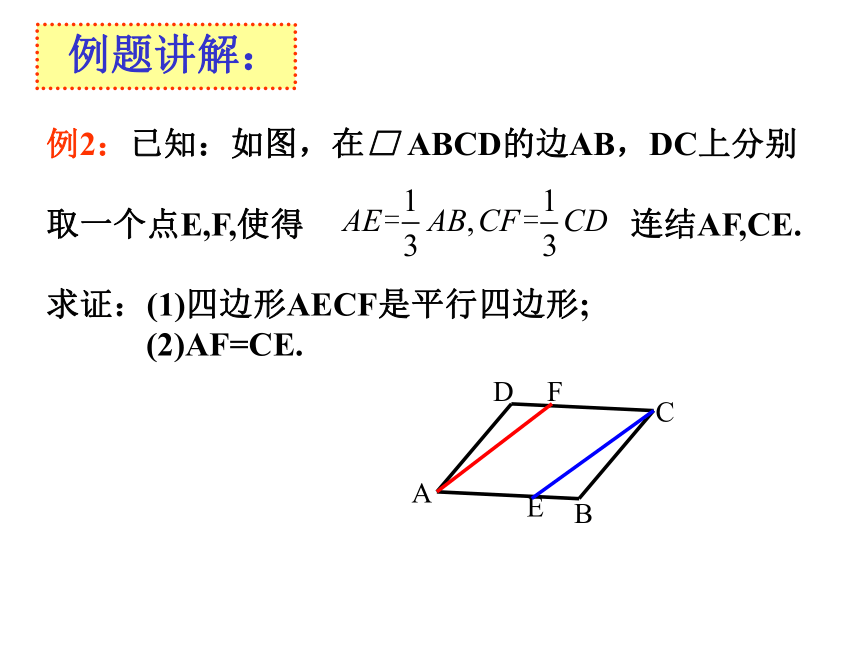
求证:四边形EBFD是平行四边形. 例题讲解:例2:已知:如图,在□ ABCD的边AB,DC上分别
取一个点E,F,使得 连结AF,CE.
求证:(1)四边形AECF是平行四边形;
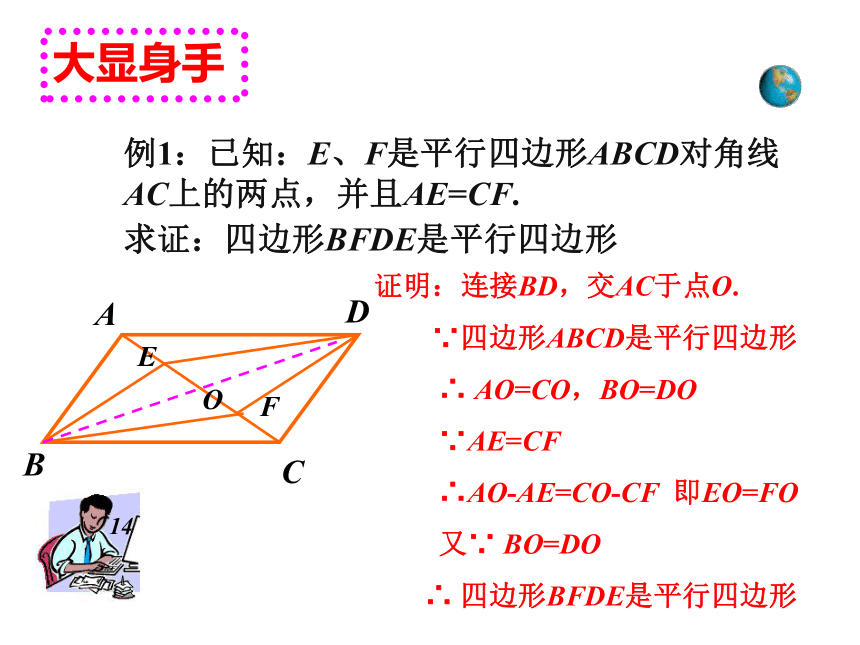
(2)AF=CE.例1:已知:E、F是平行四边形ABCD对角线AC上的两点,并且AE=CF.DOABCEF证明:连接BD,交AC于点O.
∵四边形ABCD是平行四边形
∴ AO=CO,BO=DO
∵AE=CF
∴AO-AE=CO-CF 即EO=FO
又∵ BO=DO
∴ 四边形BFDE是平行四边形大显身手求证:四边形BFDE是平行四边形14你今天有何收获? 平行四边形的判定方法1.定义法: 两组对边分别平行的四边形是平行四边形。2.判定定理1:对角线互相平分的四边形是平行四边形。3.判定定理2: 一组对边平行且相等的四边形是平行四边形。课 堂 小 结2.2.2 平行四边形的判定(二) 平行四边形的判定方法1.定义法: 两组对边分别平行的四边形是平行四边形。2.判定定理1:对角线互相平分的四边形是平行四边形。3.判定定理2: 一组对边平行且相等的四边形是平行四边形。温故知新平行四边形对边相等;平行四边形对角相等.平行四边形的性质:平行四边形对边平行;AB∥CD;AD∥BCAB=CD;AD=BC∠A=∠C,∠D=∠B平行四边形的对角线互相平分AO=CO, BO=DO 那么反过来,对边
相等或对角相等的
四边形是否是平行
四边形?边边角对角线温故知新 将两长两短的四根细木条用小钉绞合在一起,做成一个四边形,使等长的木条成为对边.转动这个四边形,使它形状改变,在图形变化的过程中,它一直是一个平行四边形吗?新知探究1从实验结果得出什么结论?ABCD观察与思考 ∴△ABC≌△CDA(SSS)ABDC证明:已知:AB=CD,AD=BC连接AC在 ABC和 CDA中AB=CD
AD=CB
AC=CA
1= 2, 3= 4 四边形ABCD是平行四边形AB ∥ CD,AD ∥ BC求证:四边形ABCD是平行四边形两组对边分别相等的四边形是平行四边形。命题:两组对边分别相等的四边形是平行四边形。判定定理3已知:如图,四边形ABCD中,∠A=∠C,∠B=∠D.
求证:四边形ABCD是平行四边形.命题:两组对角分别相等的四边形是平行四边形。证明:A= C, B= DA+ C+ B+ D=360在四边形ABCD中2( A+ B)=360 A+ B=180同理:AD ∥ BCAB ∥ CD四边形ABCD是平行四边形两组对角分别相等的四边形是平行四边形。判定定理4两组对边分别平行的四边形是平行四边形∵AB∥CD,
AD∥BC
∴四边形ABCD是平行四边形两组对边分别相等的四边形是平形四边形∵AB=CD,
AD= BC
∴四边形ABCD是平行四边形对角线互相平分的四边形是平行四边形∵OA=OC,
OB=OD
∴四边形ABCD是平行四边形两组对角分别相等的四边形是平行四边形∵∠A=∠C,
∠B=∠D
∴四边形ABCD是平行四边形 一组对边平行且相等的四边形是平行四边形∵AB∥CD,
AB=CD
∴四边形ABCD是平行四边形下列四边形是不是平行四边形?请说出理由说一说如图,AB =DC=EF, AD=BC,DE=CF,则图中有哪些互相平行的线段?试一试AB ∥ DC∥ EFAD ∥ BCDE ∥ CF求证:四边形BFDE是平行四边形.例1.已知: ABCD的对角线AC、BD相交于点O, E、F是对角线AC上的两点,并且AE=CF.证明: ∵四边形ABCD是平行四边形
∴ AO=CO,BO=DO
∵AE=CF
∴AO-AE=CO-CF
∴EO=FO
又 BO=DO
∴ 四边形BFDE是平行四边形你还有其他证明方法吗?判定运用证明:四边形ABCD是平行四边形AD ∥ BC且AD =BCEAD= FCBAE=CF
EAD= FCB
AD=BCAED ≌ CFB(SAS)DE=BF四边形BFDE是平行四边形在 AED和 CFB中同理可证:BE=DFFE求证:四边形BFDE是平行四边形.例3.已知: ABCD的对角线AC、BD相交于点O, E、F是对角线AC上的两点,并且AE=CF.大显身手如图,在 ABCD中,已知AE、CF分别是∠DAB、∠BCD的角平分线,
61234785求证:四边形AECF是平行四边形。你今天有何收获?两组对边分别平行的四边形是平行四边形∵AB∥CD,
AD∥BC
∴四边形ABCD是平行四边形两组对边分别相等的四边形是平形四边形∵AB=CD,
AD= BC
∴四边形ABCD是平行四边形对角线互相平分的四边形是平行四边形∵OA=OC,
OB=OD
∴四边形ABCD是平行四边形两组对角分别相等的四边形是平行四边形∵∠A=∠C,
∠B=∠D
∴四边形ABCD是平行四边形 一组对边平行且相等的四边形是平行四边形∵AB∥CD,
AB=CD
∴四边形ABCD是平行四边形
相等或对角相等
或对角线互相平
分的四边形是否
是平行四边形?边边角对角线 如图,将两根细木条AC、BD的中点重叠,用小钉绞合在一起,用橡皮筋连接木条的顶点,做成一个四边形ABCD.转动两根木条,四边形ABCD一直是一个平行四边形吗?新知探究1 从实验结果得出什么结论?BDOAC 对角线互相平分的四边形是平行四边形。结论:O已知:OA=OC, OB=OD
求证:四边形ABCD是平行四边形CA证明:在 ABO和 CDO中OA=OC
AOB= COD
OB=OD
ABO≌ CDO(SAS) AB=CD同理:AD=BC 四边形ABCD是平行四边形证明: 对角线互相平分的四边形是平行四边形。对角线互相平分的四边形是平行四边形。判定定理1四边形ABCD是什么样的图形?猜测: 将一根木棒从AB平移到DC,AB与DC之间的位置关系、数量关系?新知探究2一组对边平行且相等的四边形是平行四边形 。证明:一组对边平行且相等的四边形是平行四边形已知:AB∥CD, AB=CD求证:四边形ABCD是平行
四边形证明:连接BD 一组对边平行且相等的四边形是平行四边形。判定定理2∵AB=CD且AB∥CD,
∴四边形ABCD是平行四边形. 符号语言:或∵AD=BC且AD∥BC,
∴四边形ABCD是平行四边形. 注意:一组对边平行,另一组对边相等的四边形不一定是平行四边形。 平行四边形的判定方法1.定义法: 两组对边分别平行的四边形是平行四边形。2.判定定理1:对角线互相平分的四边形是平行四边形。3.判定定理2: 一组对边平行且相等的四边形是平行四边形。 例题讲解:例1:已知:如图,在□ ABCD的对角线AC上取
两点E,F,使得点E和点F关于交点O对称,连结
EB,ED,FB,FD.
求证:四边形EBFD是平行四边形. 例题讲解:例2:已知:如图,在□ ABCD的边AB,DC上分别
取一个点E,F,使得 连结AF,CE.
求证:(1)四边形AECF是平行四边形;
(2)AF=CE.例1:已知:E、F是平行四边形ABCD对角线AC上的两点,并且AE=CF.DOABCEF证明:连接BD,交AC于点O.
∵四边形ABCD是平行四边形
∴ AO=CO,BO=DO
∵AE=CF
∴AO-AE=CO-CF 即EO=FO
又∵ BO=DO
∴ 四边形BFDE是平行四边形大显身手求证:四边形BFDE是平行四边形14你今天有何收获? 平行四边形的判定方法1.定义法: 两组对边分别平行的四边形是平行四边形。2.判定定理1:对角线互相平分的四边形是平行四边形。3.判定定理2: 一组对边平行且相等的四边形是平行四边形。课 堂 小 结2.2.2 平行四边形的判定(二) 平行四边形的判定方法1.定义法: 两组对边分别平行的四边形是平行四边形。2.判定定理1:对角线互相平分的四边形是平行四边形。3.判定定理2: 一组对边平行且相等的四边形是平行四边形。温故知新平行四边形对边相等;平行四边形对角相等.平行四边形的性质:平行四边形对边平行;AB∥CD;AD∥BCAB=CD;AD=BC∠A=∠C,∠D=∠B平行四边形的对角线互相平分AO=CO, BO=DO 那么反过来,对边
相等或对角相等的
四边形是否是平行
四边形?边边角对角线温故知新 将两长两短的四根细木条用小钉绞合在一起,做成一个四边形,使等长的木条成为对边.转动这个四边形,使它形状改变,在图形变化的过程中,它一直是一个平行四边形吗?新知探究1从实验结果得出什么结论?ABCD观察与思考 ∴△ABC≌△CDA(SSS)ABDC证明:已知:AB=CD,AD=BC连接AC在 ABC和 CDA中AB=CD
AD=CB
AC=CA
1= 2, 3= 4 四边形ABCD是平行四边形AB ∥ CD,AD ∥ BC求证:四边形ABCD是平行四边形两组对边分别相等的四边形是平行四边形。命题:两组对边分别相等的四边形是平行四边形。判定定理3已知:如图,四边形ABCD中,∠A=∠C,∠B=∠D.
求证:四边形ABCD是平行四边形.命题:两组对角分别相等的四边形是平行四边形。证明:A= C, B= DA+ C+ B+ D=360在四边形ABCD中2( A+ B)=360 A+ B=180同理:AD ∥ BCAB ∥ CD四边形ABCD是平行四边形两组对角分别相等的四边形是平行四边形。判定定理4两组对边分别平行的四边形是平行四边形∵AB∥CD,
AD∥BC
∴四边形ABCD是平行四边形两组对边分别相等的四边形是平形四边形∵AB=CD,
AD= BC
∴四边形ABCD是平行四边形对角线互相平分的四边形是平行四边形∵OA=OC,
OB=OD
∴四边形ABCD是平行四边形两组对角分别相等的四边形是平行四边形∵∠A=∠C,
∠B=∠D
∴四边形ABCD是平行四边形 一组对边平行且相等的四边形是平行四边形∵AB∥CD,
AB=CD
∴四边形ABCD是平行四边形下列四边形是不是平行四边形?请说出理由说一说如图,AB =DC=EF, AD=BC,DE=CF,则图中有哪些互相平行的线段?试一试AB ∥ DC∥ EFAD ∥ BCDE ∥ CF求证:四边形BFDE是平行四边形.例1.已知: ABCD的对角线AC、BD相交于点O, E、F是对角线AC上的两点,并且AE=CF.证明: ∵四边形ABCD是平行四边形
∴ AO=CO,BO=DO
∵AE=CF
∴AO-AE=CO-CF
∴EO=FO
又 BO=DO
∴ 四边形BFDE是平行四边形你还有其他证明方法吗?判定运用证明:四边形ABCD是平行四边形AD ∥ BC且AD =BCEAD= FCBAE=CF
EAD= FCB
AD=BCAED ≌ CFB(SAS)DE=BF四边形BFDE是平行四边形在 AED和 CFB中同理可证:BE=DFFE求证:四边形BFDE是平行四边形.例3.已知: ABCD的对角线AC、BD相交于点O, E、F是对角线AC上的两点,并且AE=CF.大显身手如图,在 ABCD中,已知AE、CF分别是∠DAB、∠BCD的角平分线,
61234785求证:四边形AECF是平行四边形。你今天有何收获?两组对边分别平行的四边形是平行四边形∵AB∥CD,
AD∥BC
∴四边形ABCD是平行四边形两组对边分别相等的四边形是平形四边形∵AB=CD,
AD= BC
∴四边形ABCD是平行四边形对角线互相平分的四边形是平行四边形∵OA=OC,
OB=OD
∴四边形ABCD是平行四边形两组对角分别相等的四边形是平行四边形∵∠A=∠C,
∠B=∠D
∴四边形ABCD是平行四边形 一组对边平行且相等的四边形是平行四边形∵AB∥CD,
AB=CD
∴四边形ABCD是平行四边形
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
