2.2.1直线的点斜式方程 课件(共18张PPT)
文档属性
| 名称 | 2.2.1直线的点斜式方程 课件(共18张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-19 14:23:19 | ||
图片预览



文档简介
(共18张PPT)
2.2.1 直线的点斜式方程
第二章 直线和圆的方程
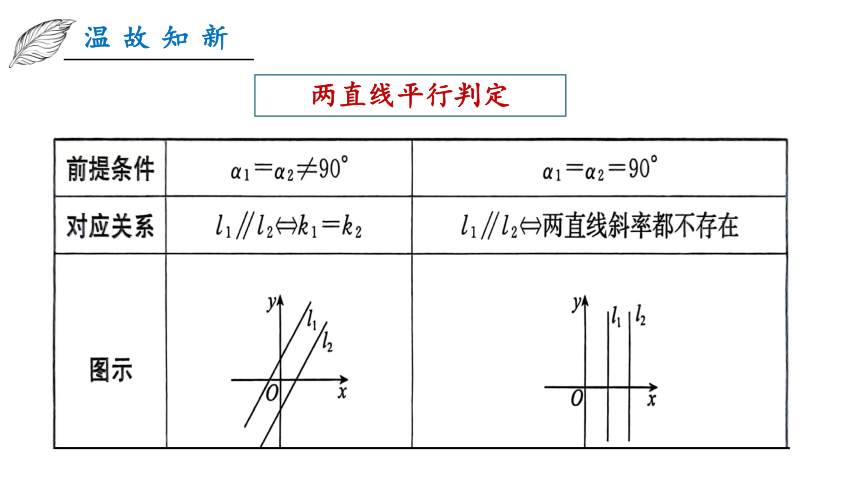
两直线平行判定
温故知新
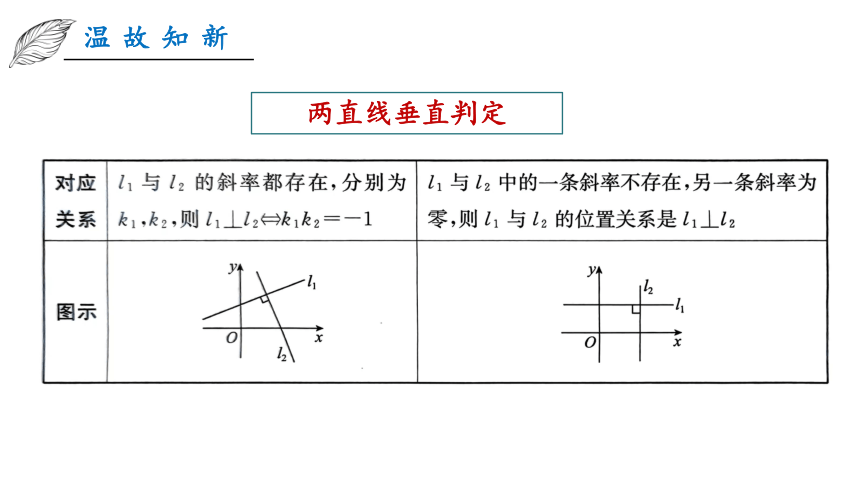
两直线垂直判定
温故知新
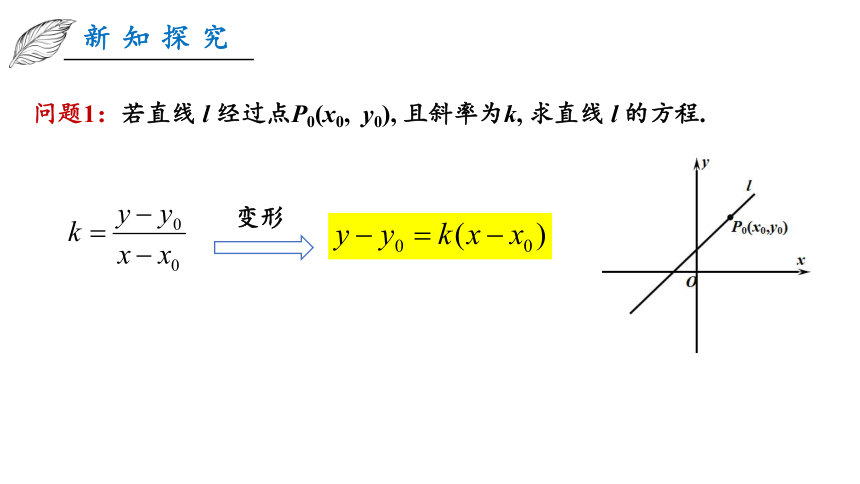
新知探究
问题1:若直线 l 经过点P0(x0, y0), 且斜率为k, 求直线 l 的方程.
变形
知识点1、直线的点斜式方程
y - y 0 = k ( x - x 0 )
方程由直线上一个定点及该直线的斜率 确定,我们把它叫做直线的点斜式方程,简称点斜式。
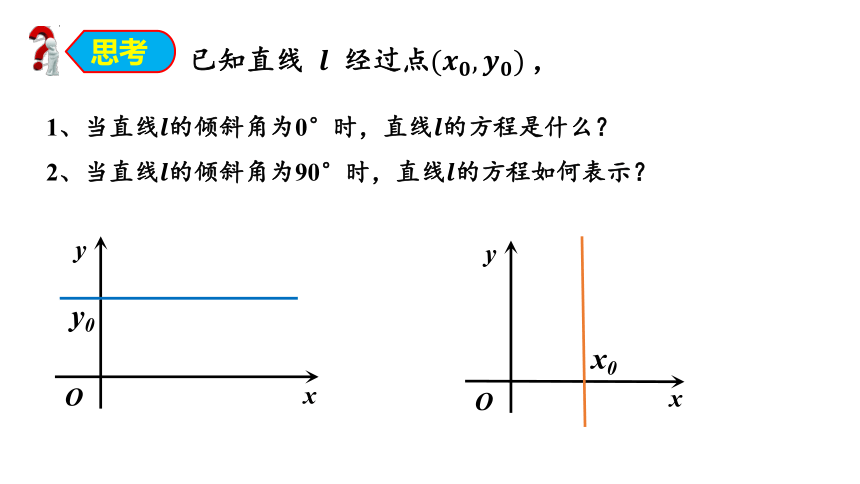
思考
1、当直线的倾斜角为0°时,直线的方程是什么?
2、当直线的倾斜角为90°时,直线的方程如何表示?
已知直线 经过点,
O
x
y
y0
O
x
y
x0
例题讲解
例1、根据条件写出下列直线的点斜式方程
(1)过点P(-4, 3),斜率k=-3
(2)过点P(3, -4),且与x轴平行
(3)过点P(3, -4),且与y轴平行
(4)过P(-2, 3),Q(5, -4)
思考2: 若给出直线斜率为k, 且与y轴的交点为(0, b), 则直线的方程是什么
O
x
y
b
方程: y - b = k ( x - 0 )
即: y = kx + b
把 b 叫做直线在 y 轴上的截距.
思考
知识点2、直线的斜截式方程
注意: 1. 截距 b 不是距离,而是直线与y轴交点的纵坐标,可正可负可为0;可将纵截距看成直线l过(0, b)
y = k x + b
2.直线的横截距a表示直线在x轴上的截距,它是直线与x轴交点的横坐标。可将横截距看成直线l过(a, 0)
这个方程是由斜率与直线在y轴上的截距确定的, 叫做直线方程的斜截式,斜截式是点斜式的特殊情况。 其中k表示直线的斜率,b表示直线在y轴的截距。
例2:写出下列直线的斜截式方程:
(1)经过点(3,-1),斜率是;
(2)经过点(,2),倾斜角是30°;
(3)过(-2,3),(5,-4)两点.
知识点3、根据直线的斜截式方程判断两直线平行与垂直
对于直线l1:y=k1x+b1,l2:y=k2x+b2,
(1)l1∥l2 ____________________________;
(2)l1⊥l2 __________________.
k1=k2,且b1≠b2
k1k2=-1
例3、已知直线l1:y=x+2与l2:y=-2ax+1平行,则a=________.
例4、求经过点(0,2),且与直线y= -3x-5平行的直线方程,并求其横纵截距;
例5、求经过点(-1,1),且与直线y= -2x+7垂直的直线方程
例6、已知直线l:5ax-5y-a+3=0.
(1)求证:不论实数a为何值,直线l总经过第一象限;
(2)若直线l不经过第二象限,求实数a的取值范围。
例7、已知直线l:y=kx+2k+1.
(1)求证:直线l过定点;
(2)若当-3题型巩固
1.已知在第一象限的△ABC中,A(1,1),B(5,1),∠A=60°,∠B=45°,求:
(1)AB边所在直线的方程;
(2)AC边与BC边所在直线的方程.
2、(1)当为何值时,直线:与直线:平行?
(2)当为何值时,直线:与直线:垂直?
4.已知两点A(-2,0),B(0,4),则线段AB的垂直平分线的方程为
__________.
3、已知直线l1:y=kx+b,l2:y=bx+k,则它们的图象可能为( )
归纳总结
点斜式 斜截式
已知条件 点和斜率 斜率与直线在轴上的截距
图示
方程形式
适用条件 斜率存在的直线 备注 斜截式是特殊的点斜式方程
直线的点斜式方程
2.2.1 直线的点斜式方程
第二章 直线和圆的方程
两直线平行判定
温故知新
两直线垂直判定
温故知新
新知探究
问题1:若直线 l 经过点P0(x0, y0), 且斜率为k, 求直线 l 的方程.
变形
知识点1、直线的点斜式方程
y - y 0 = k ( x - x 0 )
方程由直线上一个定点及该直线的斜率 确定,我们把它叫做直线的点斜式方程,简称点斜式。
思考
1、当直线的倾斜角为0°时,直线的方程是什么?
2、当直线的倾斜角为90°时,直线的方程如何表示?
已知直线 经过点,
O
x
y
y0
O
x
y
x0
例题讲解
例1、根据条件写出下列直线的点斜式方程
(1)过点P(-4, 3),斜率k=-3
(2)过点P(3, -4),且与x轴平行
(3)过点P(3, -4),且与y轴平行
(4)过P(-2, 3),Q(5, -4)
思考2: 若给出直线斜率为k, 且与y轴的交点为(0, b), 则直线的方程是什么
O
x
y
b
方程: y - b = k ( x - 0 )
即: y = kx + b
把 b 叫做直线在 y 轴上的截距.
思考
知识点2、直线的斜截式方程
注意: 1. 截距 b 不是距离,而是直线与y轴交点的纵坐标,可正可负可为0;可将纵截距看成直线l过(0, b)
y = k x + b
2.直线的横截距a表示直线在x轴上的截距,它是直线与x轴交点的横坐标。可将横截距看成直线l过(a, 0)
这个方程是由斜率与直线在y轴上的截距确定的, 叫做直线方程的斜截式,斜截式是点斜式的特殊情况。 其中k表示直线的斜率,b表示直线在y轴的截距。
例2:写出下列直线的斜截式方程:
(1)经过点(3,-1),斜率是;
(2)经过点(,2),倾斜角是30°;
(3)过(-2,3),(5,-4)两点.
知识点3、根据直线的斜截式方程判断两直线平行与垂直
对于直线l1:y=k1x+b1,l2:y=k2x+b2,
(1)l1∥l2 ____________________________;
(2)l1⊥l2 __________________.
k1=k2,且b1≠b2
k1k2=-1
例3、已知直线l1:y=x+2与l2:y=-2ax+1平行,则a=________.
例4、求经过点(0,2),且与直线y= -3x-5平行的直线方程,并求其横纵截距;
例5、求经过点(-1,1),且与直线y= -2x+7垂直的直线方程
例6、已知直线l:5ax-5y-a+3=0.
(1)求证:不论实数a为何值,直线l总经过第一象限;
(2)若直线l不经过第二象限,求实数a的取值范围。
例7、已知直线l:y=kx+2k+1.
(1)求证:直线l过定点;
(2)若当-3
1.已知在第一象限的△ABC中,A(1,1),B(5,1),∠A=60°,∠B=45°,求:
(1)AB边所在直线的方程;
(2)AC边与BC边所在直线的方程.
2、(1)当为何值时,直线:与直线:平行?
(2)当为何值时,直线:与直线:垂直?
4.已知两点A(-2,0),B(0,4),则线段AB的垂直平分线的方程为
__________.
3、已知直线l1:y=kx+b,l2:y=bx+k,则它们的图象可能为( )
归纳总结
点斜式 斜截式
已知条件 点和斜率 斜率与直线在轴上的截距
图示
方程形式
适用条件 斜率存在的直线 备注 斜截式是特殊的点斜式方程
直线的点斜式方程
