第十二章 全等三角形专题强化(无答案) 2024-2025学年人教版八年级数学上册
文档属性
| 名称 | 第十二章 全等三角形专题强化(无答案) 2024-2025学年人教版八年级数学上册 |
|
|
| 格式 | docx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-18 00:00:00 | ||
图片预览


文档简介
全等三角形专题强化
专题一 几何作图与多解问题
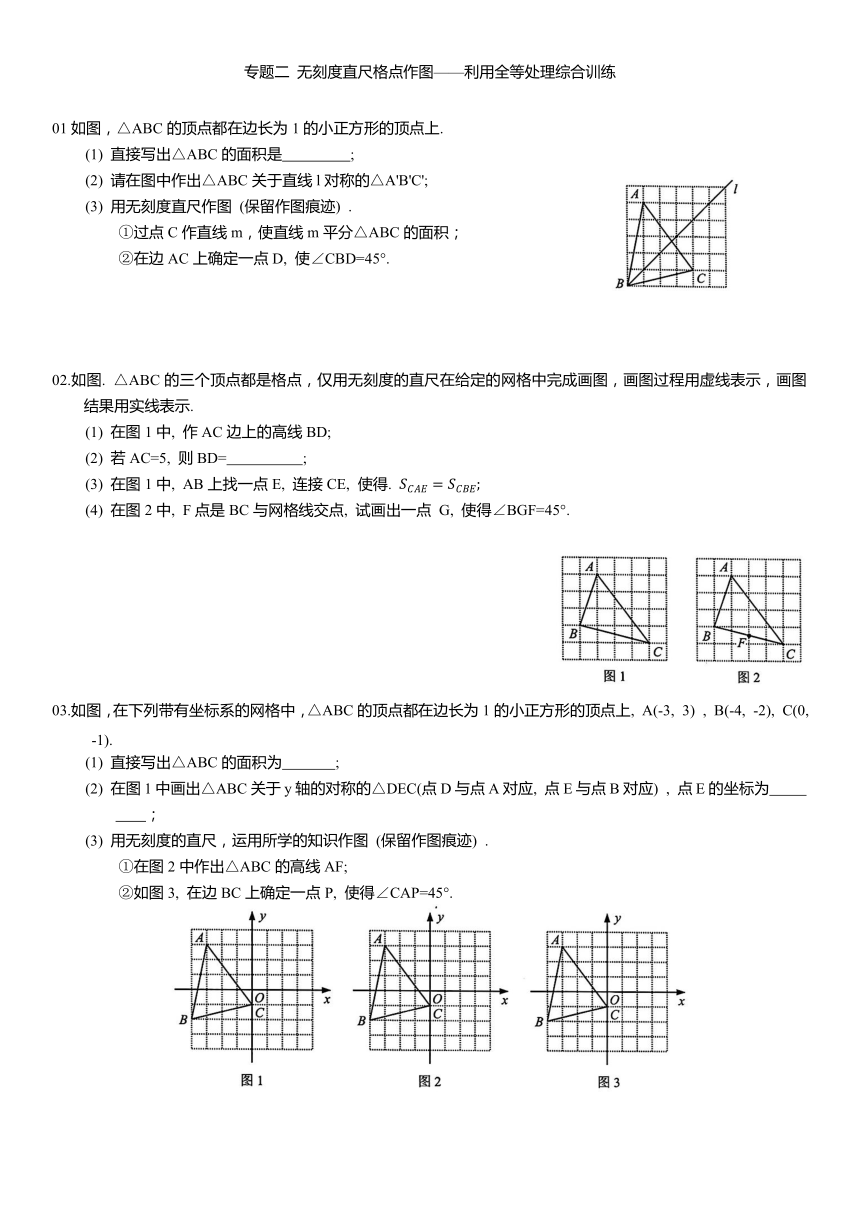
01如图, 在方格纸中,以AB为一边作△ABP, 使之与△ABC全等, 从P , P , P ,P 四个点中找出符合条件的点P,则这样的点P有 ( )
A. 1个 B. 2个
C. 3个 D. 4个
02如图, 在方格纸中, 以AB为一边作△ABP, 使之与△ABC全等, 则这样的点P有( ).(不含△ABC)
A. 1个 B. 2个
C. 3个 D. 4个
03.如图,3×4的网格中,△ABC的三个顶点均在格点上,这样的三角形叫格点三角形,图中可以画出与△ABC全等的格点三角形共有 ( )个(不含△ABC)
A. 23 B. 24
C. 27 D. 28
04.如图, CA⊥AB, 垂足为点A, AB=24, AC=12, 射线BM⊥AB, 垂足为点B, 一动点E从A 点出发以3厘米/秒沿射线AN运动,点D 为射线BM上一动点,随着E点运动而运动,且始终保持ED=CB, 当点E经过t秒时(t>0) , △DEB 与△BCA1全等,则t的值为 .
专题二 无刻度直尺格点作图——利用全等处理综合训练
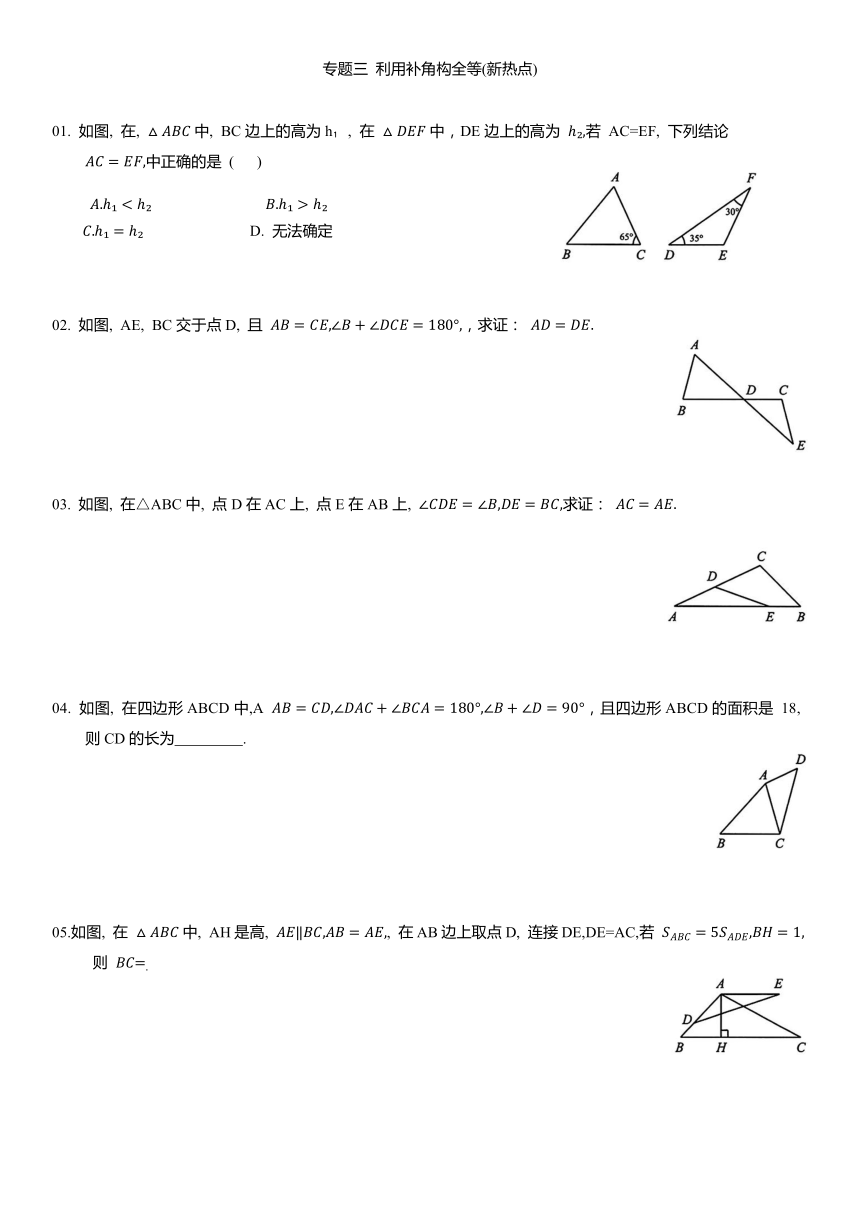
01如图,△ABC的顶点都在边长为1的小正方形的顶点上.
(1) 直接写出△ABC的面积是 ;
(2) 请在图中作出△ABC关于直线l对称的△A'B'C';
(3) 用无刻度直尺作图 (保留作图痕迹) .
①过点C作直线m,使直线m平分△ABC的面积;
②在边AC上确定一点D, 使∠CBD=45°.
02.如图. △ABC的三个顶点都是格点,仅用无刻度的直尺在给定的网格中完成画图,画图过程用虚线表示,画图结果用实线表示.
(1) 在图1中, 作AC边上的高线BD;
(2) 若AC=5, 则BD= ;
(3) 在图1中, AB上找一点E, 连接CE, 使得.
(4) 在图2中, F点是BC与网格线交点, 试画出一点 G, 使得∠BGF=45°.
03.如图,在下列带有坐标系的网格中,△ABC的顶点都在边长为1的小正方形的顶点上, A(-3, 3) , B(-4, -2), C(0, -1).
(1) 直接写出△ABC的面积为 ;
(2) 在图1中画出△ABC关于y轴的对称的△DEC(点D与点A对应, 点E与点B对应) , 点E的坐标为 ;
(3) 用无刻度的直尺,运用所学的知识作图 (保留作图痕迹) .
①在图2中作出△ABC的高线AF;
②如图3, 在边BC上确定一点P, 使得∠CAP=45°.
专题三 利用补角构全等(新热点)
01. 如图, 在, 中, BC边上的高为h , 在 中,DE边上的高为 若 AC=EF, 下列结论 中正确的是 ( )
D. 无法确定
02. 如图, AE, BC交于点D, 且 ,求证:
03. 如图, 在△ABC中, 点D在AC上, 点E在AB上, 求证:
04. 如图, 在四边形ABCD中,A ,且四边形ABCD的面积是 18, 则CD的长为 .
05.如图, 在 中, AH是高, , 在AB边上取点D, 连接DE,DE=AC,若 则
专题四 边边角(SSA)问题的处理方法 (新热点 )
方法:边边角即SSA问题,放垂处理
01. 如图,把长短确定的两根木棍AB,AC的一端固定在A处,和第三根木棍BM摆出△ABC,木棍AB固定, 木棍AC绕A转动, 得到△ABD, 这个实验说明( )
A. 三角形具有稳定性
B. 面积相等的两个三角形不一定全等
C. 两边和它们的夹角分别相等的两个三角形全等
D. 有两边和其中一边的对角分别相等的两个三角形不一定全等
02如图, OC在∠AOB内部, P是OC上的一点, 点D, E分别在OA, OB上, 且OD=OE, 连接PD, PE, ∠PDO>90°, ∠PDO=∠PEO. 求证: OC平分∠AOB.
03. 如图, 在等腰△ABC中, AB=AC, D是BC边上的一个动点, 射线( , 且AD=DE, 猜想∠ABC与∠ADE的数量关系,并证明你的结论.
04. 如图, 已知 是边长为5的等边三角形,点E 在CA 的延长线上且 , 连接EB, 在线段BC上取一点F,使得. 连接EF, 求BF的长.
专题五 利用角平分线的性质求线段长
核心考点一 放垂直接应用角平分线定理
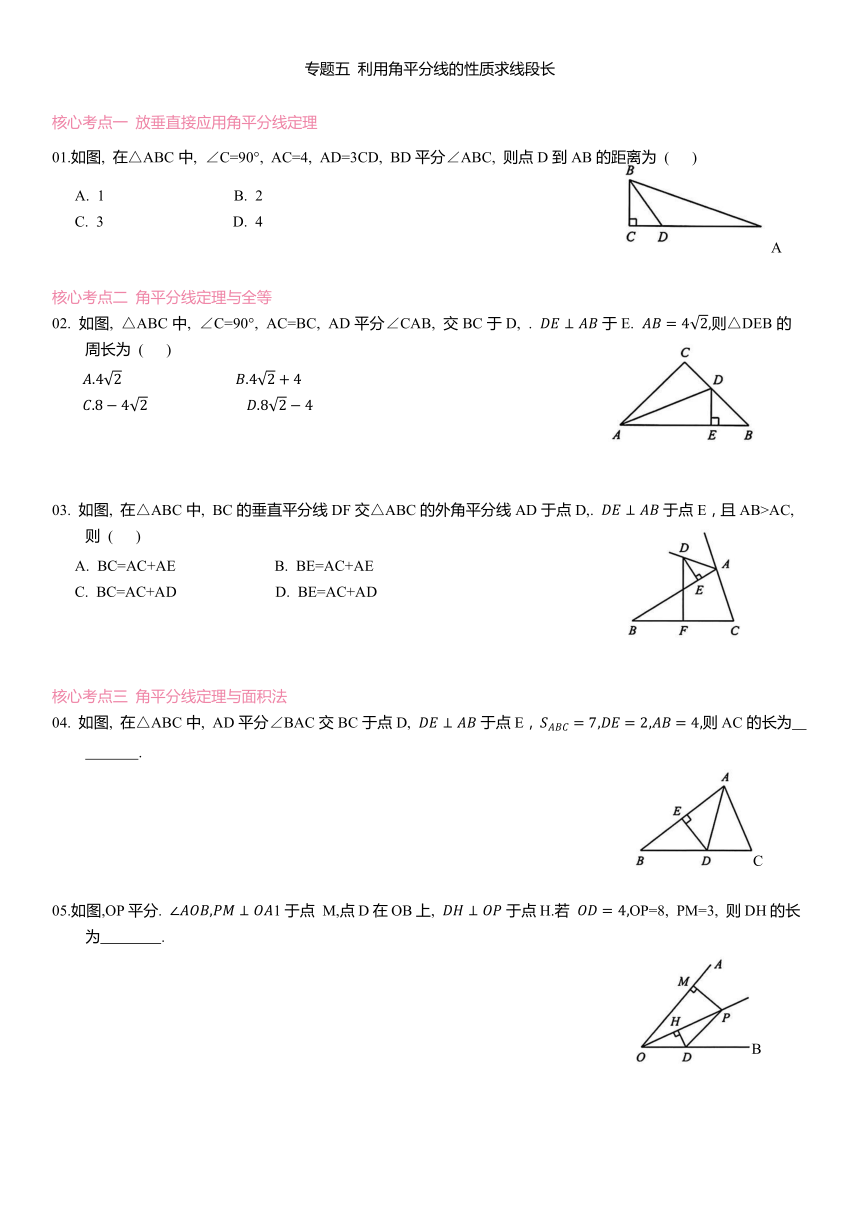
01.如图, 在△ABC中, ∠C=90°, AC=4, AD=3CD, BD平分∠ABC, 则点D到AB的距离为 ( )
A. 1 B. 2
C. 3 D. 4
A
核心考点二 角平分线定理与全等
02. 如图, △ABC中, ∠C=90°, AC=BC, AD平分∠CAB, 交BC于D, . 于E. 则△DEB的周长为 ( )
03. 如图, 在△ABC中, BC的垂直平分线DF交△ABC的外角平分线AD于点D,. 于点E,且AB>AC, 则 ( )
A. BC=AC+AE B. BE=AC+AE
C. BC=AC+AD D. BE=AC+AD
核心考点三 角平分线定理与面积法
04. 如图, 在△ABC中, AD平分∠BAC交BC于点D, 于点E, 则AC的长为 .
C
05.如图,OP平分. 1于点 M,点D在OB上, 于点H.若 OP=8, PM=3, 则DH的长为 .
B
06.如图, Rt△ABC中, ∠ABC=90°, AB=6, BC=8, BD为△ABC的角平分线, 则点D到边AB的距离为 .
核心考点四 角平分线性质定理与分类讨论
07.如图, 点P是∠AOB的角平分线OC上一点, PN⊥OB于点N, 点M是线段ON上一点, 已知OM=3, ON=4, 点D为OA上一点, 若满足PD=PM, 则OD的长度为 .
核心考点五 角平分线性质定理与全等和面积法结合
08.如图, BE是Rt△ABC的角平分线, AD⊥BC, 垂足为D, AD, BE交于点G, 过点G 作BC的平行线交AC于点F. 若AB=6, AC=8, BC=10, 则
09.如图, 四边形ABCD中, ∠DAB+∠ABC=90°, 对角线AC, BD相交于 O 点, 且分别平分∠DAB和∠ABC, 若BO=4OD, 则 的值为 .
专题六 全等辅助线与模型进阶(1)——内心、旁心与隐藏的角平分线
核心考点一 内角平分线的交点——内心,与对称全等推导线段关系
01. 如图, 在△ABC中, ∠ABC=90°, 点I为△ABC各内角平分线的交点, 过I点作AC的垂线, 垂足为H, 若BC=3, AB=4, AC=5, 那么IH的值为 .
02.如图,在△ABC中,AB=8,BC=10,AC=7,∠ABC和∠ACB的平分线交于点I,IE⊥BC于E, 则BE的长为 .
03.如图, 在 Rt△ACB中, ∠ACB=90°, AC=6, BC=8, AI平分∠CAB, BI平分∠ABC,过点I作IG⊥AB 于G, 若BG=6, 则△ABI的面积为 .
核心考点二 隐藏的角平分线与旁心(两条外角平分线的交点或一内一外角平分线的交点)
04.如图, 在四边形ABCD 中, 对角线BD平分∠ABC, ∠ACB=74°, ∠ABC=46°, 且∠BAD+∠CAD=180°, 那么∠BDC的度数为 .
05.如图, 在四边形ABDC中, 对角线AD平分 BCD=44°, 则 的度数为 .
06.如图, 在. 中, 点M, N是 与 三等分线的交点,若 则∠BMN的度数是 .
C
07.如图, 在等腰△ABC中, 顶角∠A=45°, 点E, F是内角∠ABC与外角. 三等分线的交点, 连接EF, 则∠BFE= °.
08.如图,平面上到两两相交的三条直线a,b,c的距离都相等的点一共有( . )
A. 1个 B. 2个
C. 3个 D. 4个
09.如图, △ABC的∠BAC和∠BCA的外角角平分线交于点O, 若 AB=OC-AC,∠OCA=x°, 其中 ,则∠OAC的度数是 °. (用含x的式子表示)
专题七 全等辅助线与模型进阶(2)——内角平分线定理的初步认识
01.如图,在△ABC中,AD是它的角平分线, ,则CD的长为( )
B. 4
C. 4.5 D. 6
02.如图, 在△ABC中, ∠ACB=90°, AD是∠BAC的角平分线, 若AB∶AC=3∶2, 且BD=2, 则点D到直线AB的距离为 .
03如图, 在Rt△ABC中, ∠C=90°, BE平分∠ABC交AC于点E, 点D是BC的中点,连接AD交BE于点F. 若AC=4, BC=3, AB=5, 则
04.如图, 在△ABE内有一点D, 点C是AE上一点, AD交BE于点P, 射线DC交BE的延长线于点 F, 且∠ABD=∠ACD, ∠PDB=∠PDC.
(1) 求证: AB=AC;
(2)若AB=3, AE=5, 求 的值;
(3) 若 则 (用m表示)
专题八 全等辅助线与模型进阶(3)——中点模型之放垂或作平行构等腰
方法:作平行构等腰或放垂构造8字型全等证中点
核心考点一 等腰三角形中的剪刀图
01. 如图, 中, , 点D在AB上, 点E在AC的延长线上, DE交BC于F且, 求证:
核心考点二 旋转得等腰
02. 如图, 中, 将 绕C 点顺时针旋转一个角度得到 直线BD交AE于点M, 求证: M为AE的中点.
专题九 全等辅助线与模型进阶 (4)——夹半角与截长补短
01. 如图, 在五边形ABCDE中, 且 CD=3,AE=4, 则五边形ABCDE的面积为 ( )
A. 6 B. 8
C. 10 D. 12
02. 如图, 等腰Rt△OAB中, ,过点A作 ,若线段OA上一点C满足∠CDB=∠OBD, 则∠CBD的大小是 ( )
A. 30° B. 40°
C. 45° D. 60°
03. 如图, 平面直角坐标系中, A(-4, 0) , B(0, 4) , M是AB中点, E是线段OA上一动点, F在y轴负半轴上, AE+OF=EF, 求. 的度数.
04.如图, 在平面直角坐标系中, 点A(0, 2), B (2, 0) , 点C在. 的平分线上, 求 的度数.
05. 如图, B(4, 4) , BC⊥y轴于点C, . 轴于点A, E为BC上一动点(不与B, C重合), F为AB上一动点, 且满足∠OEF=∠AOE, 在运动过程中, 求 的周长.
06.如图, △ABC中, AB=AC=DE, D为BC延长线上一点, 过点D作 于E交AC于F, 若AB=m, AF=n, 则. (用含m,n的式子表示)
07. 在△ABC中, AB=AC, ∠BAC=90°, 点E在边BC上, 点F在射线EC上, 且
(1) 如图1, 画出△AEF关于直线AF对称的△AE'F, 并写出画法;
(2) 如图2, 若∠AFE=75°, 求 的值;
(3) 如图3, 若BE=CF, 直接写出∠AFE的度数为 .
专题十 全等辅助线与模型进阶(5)——中点线段倍长构全等之脚碰脚
核心考点一 第一次全等后得对应边平行且相等后,再利用对角互补型导角
01. 如图, 已知 和 均为等腰直角三角形, , 点M为CE中点. 求证:①BM⊥DM; ②BM=DM.
核心考点二 第一次全等后得对应边平行且相等后,再利用8字型导角
02. 如图, 与 均为等腰直角三角形,共底角顶点C,连接BE取其中点M,连接AM,DM. 求证: ①AM⊥DM; ②AM=DM.
核心考点三 第一次全等后得对应边平行且相等后,再利用周角导角
03. 如图, 分别以 的边AB,AC为底边向外作等腰, 与等腰 其中 , F为BC的中点, 连接DF, EF, 猜想DF与EF的位置关系,并说明理由.
专题十一 全等辅助线与模型进阶(6)——弦图与镜面角
核心考点一 模型认识
01. 如图, 在△ABC中, ∠CAB=∠CBA=45°, CA=CB, 点E为BC的中点,( 交AB于点N,连接EN, 求证: AE=CN+EN.
核心考点二 模型变式
02. 如图, 在△ABC中,. .若M, D为AC上两点, 且. 于E点且交BC于F点, 延长BD交直线FM于点P, 求证: PD=PM.
03.如图, 在Rt△ABC中, , 点D, E分别在边AC, BC上, 过点E作EF⊥BD于点H,交AB于点F. 连接DF, 若. 求证:
核心考点三 模型应用
04.如图, 已知等腰 D在的CA延长线上,E在AC的延长线上, 连接BE,过点A作BE的垂线交BC于点F,垂足为O,连接DF并延长交BE于点K, 求BE的长度 .
专题十二 全等辅助线与模型进阶 (7)
——特殊角 与等腰直角三角形的构造
核心考点一 已有等腰直角三角形,利用 构造等腰直角三角形得手拉手
01.如图, 在等腰 中,
(1) 求证:
(2) 若BD=6, CD=2, 求四边形ABCD的面积.
核心考点二 利用45°构造等腰直角三角形,利用8字型构造旋转型全等
02.如图,在Rt△ABC中,∠A=90°.点D在AB边上,点E在AC边上,满足 若DE=1, BC=7, 则,
A. 2 B. 4
C. 5 D. 6
03.如图, 在四边形ABCD中, . 求证:
核心考点三 特殊角 角的处理
04. 如图, 在△ABC中, 于点D, BE平分. 且. 于点E,与CD相交于点F,H是边BC的中点,连接DH与BE相交于点G.若GE=3,则
核心考点四 等腰直角三角形的构造综合
05已知等腰 中,
(1) 如图1, 若 连DC, 求证:
(2)如图2,若点D在AB的延长线上,以DC为斜边作等腰 ,过直角顶点E作. 于F, 求证: 点F是AC的中点.
06. 已知A(a, 0), B(0, b), a,b满足 C为OB上一点,连AC, 作 且 连BD交x轴于点E(1, 0).
(1) 求点a, b的值; (2) 求点C的坐标;
(3) 在(2) 的前提下,点F是x轴上一个动点满足 请求出点F的坐标.
专题一 几何作图与多解问题
01如图, 在方格纸中,以AB为一边作△ABP, 使之与△ABC全等, 从P , P , P ,P 四个点中找出符合条件的点P,则这样的点P有 ( )
A. 1个 B. 2个
C. 3个 D. 4个
02如图, 在方格纸中, 以AB为一边作△ABP, 使之与△ABC全等, 则这样的点P有( ).(不含△ABC)
A. 1个 B. 2个
C. 3个 D. 4个
03.如图,3×4的网格中,△ABC的三个顶点均在格点上,这样的三角形叫格点三角形,图中可以画出与△ABC全等的格点三角形共有 ( )个(不含△ABC)
A. 23 B. 24
C. 27 D. 28
04.如图, CA⊥AB, 垂足为点A, AB=24, AC=12, 射线BM⊥AB, 垂足为点B, 一动点E从A 点出发以3厘米/秒沿射线AN运动,点D 为射线BM上一动点,随着E点运动而运动,且始终保持ED=CB, 当点E经过t秒时(t>0) , △DEB 与△BCA1全等,则t的值为 .
专题二 无刻度直尺格点作图——利用全等处理综合训练
01如图,△ABC的顶点都在边长为1的小正方形的顶点上.
(1) 直接写出△ABC的面积是 ;
(2) 请在图中作出△ABC关于直线l对称的△A'B'C';
(3) 用无刻度直尺作图 (保留作图痕迹) .
①过点C作直线m,使直线m平分△ABC的面积;
②在边AC上确定一点D, 使∠CBD=45°.
02.如图. △ABC的三个顶点都是格点,仅用无刻度的直尺在给定的网格中完成画图,画图过程用虚线表示,画图结果用实线表示.
(1) 在图1中, 作AC边上的高线BD;
(2) 若AC=5, 则BD= ;
(3) 在图1中, AB上找一点E, 连接CE, 使得.
(4) 在图2中, F点是BC与网格线交点, 试画出一点 G, 使得∠BGF=45°.
03.如图,在下列带有坐标系的网格中,△ABC的顶点都在边长为1的小正方形的顶点上, A(-3, 3) , B(-4, -2), C(0, -1).
(1) 直接写出△ABC的面积为 ;
(2) 在图1中画出△ABC关于y轴的对称的△DEC(点D与点A对应, 点E与点B对应) , 点E的坐标为 ;
(3) 用无刻度的直尺,运用所学的知识作图 (保留作图痕迹) .
①在图2中作出△ABC的高线AF;
②如图3, 在边BC上确定一点P, 使得∠CAP=45°.
专题三 利用补角构全等(新热点)
01. 如图, 在, 中, BC边上的高为h , 在 中,DE边上的高为 若 AC=EF, 下列结论 中正确的是 ( )
D. 无法确定
02. 如图, AE, BC交于点D, 且 ,求证:
03. 如图, 在△ABC中, 点D在AC上, 点E在AB上, 求证:
04. 如图, 在四边形ABCD中,A ,且四边形ABCD的面积是 18, 则CD的长为 .
05.如图, 在 中, AH是高, , 在AB边上取点D, 连接DE,DE=AC,若 则
专题四 边边角(SSA)问题的处理方法 (新热点 )
方法:边边角即SSA问题,放垂处理
01. 如图,把长短确定的两根木棍AB,AC的一端固定在A处,和第三根木棍BM摆出△ABC,木棍AB固定, 木棍AC绕A转动, 得到△ABD, 这个实验说明( )
A. 三角形具有稳定性
B. 面积相等的两个三角形不一定全等
C. 两边和它们的夹角分别相等的两个三角形全等
D. 有两边和其中一边的对角分别相等的两个三角形不一定全等
02如图, OC在∠AOB内部, P是OC上的一点, 点D, E分别在OA, OB上, 且OD=OE, 连接PD, PE, ∠PDO>90°, ∠PDO=∠PEO. 求证: OC平分∠AOB.
03. 如图, 在等腰△ABC中, AB=AC, D是BC边上的一个动点, 射线( , 且AD=DE, 猜想∠ABC与∠ADE的数量关系,并证明你的结论.
04. 如图, 已知 是边长为5的等边三角形,点E 在CA 的延长线上且 , 连接EB, 在线段BC上取一点F,使得. 连接EF, 求BF的长.
专题五 利用角平分线的性质求线段长
核心考点一 放垂直接应用角平分线定理
01.如图, 在△ABC中, ∠C=90°, AC=4, AD=3CD, BD平分∠ABC, 则点D到AB的距离为 ( )
A. 1 B. 2
C. 3 D. 4
A
核心考点二 角平分线定理与全等
02. 如图, △ABC中, ∠C=90°, AC=BC, AD平分∠CAB, 交BC于D, . 于E. 则△DEB的周长为 ( )
03. 如图, 在△ABC中, BC的垂直平分线DF交△ABC的外角平分线AD于点D,. 于点E,且AB>AC, 则 ( )
A. BC=AC+AE B. BE=AC+AE
C. BC=AC+AD D. BE=AC+AD
核心考点三 角平分线定理与面积法
04. 如图, 在△ABC中, AD平分∠BAC交BC于点D, 于点E, 则AC的长为 .
C
05.如图,OP平分. 1于点 M,点D在OB上, 于点H.若 OP=8, PM=3, 则DH的长为 .
B
06.如图, Rt△ABC中, ∠ABC=90°, AB=6, BC=8, BD为△ABC的角平分线, 则点D到边AB的距离为 .
核心考点四 角平分线性质定理与分类讨论
07.如图, 点P是∠AOB的角平分线OC上一点, PN⊥OB于点N, 点M是线段ON上一点, 已知OM=3, ON=4, 点D为OA上一点, 若满足PD=PM, 则OD的长度为 .
核心考点五 角平分线性质定理与全等和面积法结合
08.如图, BE是Rt△ABC的角平分线, AD⊥BC, 垂足为D, AD, BE交于点G, 过点G 作BC的平行线交AC于点F. 若AB=6, AC=8, BC=10, 则
09.如图, 四边形ABCD中, ∠DAB+∠ABC=90°, 对角线AC, BD相交于 O 点, 且分别平分∠DAB和∠ABC, 若BO=4OD, 则 的值为 .
专题六 全等辅助线与模型进阶(1)——内心、旁心与隐藏的角平分线
核心考点一 内角平分线的交点——内心,与对称全等推导线段关系
01. 如图, 在△ABC中, ∠ABC=90°, 点I为△ABC各内角平分线的交点, 过I点作AC的垂线, 垂足为H, 若BC=3, AB=4, AC=5, 那么IH的值为 .
02.如图,在△ABC中,AB=8,BC=10,AC=7,∠ABC和∠ACB的平分线交于点I,IE⊥BC于E, 则BE的长为 .
03.如图, 在 Rt△ACB中, ∠ACB=90°, AC=6, BC=8, AI平分∠CAB, BI平分∠ABC,过点I作IG⊥AB 于G, 若BG=6, 则△ABI的面积为 .
核心考点二 隐藏的角平分线与旁心(两条外角平分线的交点或一内一外角平分线的交点)
04.如图, 在四边形ABCD 中, 对角线BD平分∠ABC, ∠ACB=74°, ∠ABC=46°, 且∠BAD+∠CAD=180°, 那么∠BDC的度数为 .
05.如图, 在四边形ABDC中, 对角线AD平分 BCD=44°, 则 的度数为 .
06.如图, 在. 中, 点M, N是 与 三等分线的交点,若 则∠BMN的度数是 .
C
07.如图, 在等腰△ABC中, 顶角∠A=45°, 点E, F是内角∠ABC与外角. 三等分线的交点, 连接EF, 则∠BFE= °.
08.如图,平面上到两两相交的三条直线a,b,c的距离都相等的点一共有( . )
A. 1个 B. 2个
C. 3个 D. 4个
09.如图, △ABC的∠BAC和∠BCA的外角角平分线交于点O, 若 AB=OC-AC,∠OCA=x°, 其中 ,则∠OAC的度数是 °. (用含x的式子表示)
专题七 全等辅助线与模型进阶(2)——内角平分线定理的初步认识
01.如图,在△ABC中,AD是它的角平分线, ,则CD的长为( )
B. 4
C. 4.5 D. 6
02.如图, 在△ABC中, ∠ACB=90°, AD是∠BAC的角平分线, 若AB∶AC=3∶2, 且BD=2, 则点D到直线AB的距离为 .
03如图, 在Rt△ABC中, ∠C=90°, BE平分∠ABC交AC于点E, 点D是BC的中点,连接AD交BE于点F. 若AC=4, BC=3, AB=5, 则
04.如图, 在△ABE内有一点D, 点C是AE上一点, AD交BE于点P, 射线DC交BE的延长线于点 F, 且∠ABD=∠ACD, ∠PDB=∠PDC.
(1) 求证: AB=AC;
(2)若AB=3, AE=5, 求 的值;
(3) 若 则 (用m表示)
专题八 全等辅助线与模型进阶(3)——中点模型之放垂或作平行构等腰
方法:作平行构等腰或放垂构造8字型全等证中点
核心考点一 等腰三角形中的剪刀图
01. 如图, 中, , 点D在AB上, 点E在AC的延长线上, DE交BC于F且, 求证:
核心考点二 旋转得等腰
02. 如图, 中, 将 绕C 点顺时针旋转一个角度得到 直线BD交AE于点M, 求证: M为AE的中点.
专题九 全等辅助线与模型进阶 (4)——夹半角与截长补短
01. 如图, 在五边形ABCDE中, 且 CD=3,AE=4, 则五边形ABCDE的面积为 ( )
A. 6 B. 8
C. 10 D. 12
02. 如图, 等腰Rt△OAB中, ,过点A作 ,若线段OA上一点C满足∠CDB=∠OBD, 则∠CBD的大小是 ( )
A. 30° B. 40°
C. 45° D. 60°
03. 如图, 平面直角坐标系中, A(-4, 0) , B(0, 4) , M是AB中点, E是线段OA上一动点, F在y轴负半轴上, AE+OF=EF, 求. 的度数.
04.如图, 在平面直角坐标系中, 点A(0, 2), B (2, 0) , 点C在. 的平分线上, 求 的度数.
05. 如图, B(4, 4) , BC⊥y轴于点C, . 轴于点A, E为BC上一动点(不与B, C重合), F为AB上一动点, 且满足∠OEF=∠AOE, 在运动过程中, 求 的周长.
06.如图, △ABC中, AB=AC=DE, D为BC延长线上一点, 过点D作 于E交AC于F, 若AB=m, AF=n, 则. (用含m,n的式子表示)
07. 在△ABC中, AB=AC, ∠BAC=90°, 点E在边BC上, 点F在射线EC上, 且
(1) 如图1, 画出△AEF关于直线AF对称的△AE'F, 并写出画法;
(2) 如图2, 若∠AFE=75°, 求 的值;
(3) 如图3, 若BE=CF, 直接写出∠AFE的度数为 .
专题十 全等辅助线与模型进阶(5)——中点线段倍长构全等之脚碰脚
核心考点一 第一次全等后得对应边平行且相等后,再利用对角互补型导角
01. 如图, 已知 和 均为等腰直角三角形, , 点M为CE中点. 求证:①BM⊥DM; ②BM=DM.
核心考点二 第一次全等后得对应边平行且相等后,再利用8字型导角
02. 如图, 与 均为等腰直角三角形,共底角顶点C,连接BE取其中点M,连接AM,DM. 求证: ①AM⊥DM; ②AM=DM.
核心考点三 第一次全等后得对应边平行且相等后,再利用周角导角
03. 如图, 分别以 的边AB,AC为底边向外作等腰, 与等腰 其中 , F为BC的中点, 连接DF, EF, 猜想DF与EF的位置关系,并说明理由.
专题十一 全等辅助线与模型进阶(6)——弦图与镜面角
核心考点一 模型认识
01. 如图, 在△ABC中, ∠CAB=∠CBA=45°, CA=CB, 点E为BC的中点,( 交AB于点N,连接EN, 求证: AE=CN+EN.
核心考点二 模型变式
02. 如图, 在△ABC中,. .若M, D为AC上两点, 且. 于E点且交BC于F点, 延长BD交直线FM于点P, 求证: PD=PM.
03.如图, 在Rt△ABC中, , 点D, E分别在边AC, BC上, 过点E作EF⊥BD于点H,交AB于点F. 连接DF, 若. 求证:
核心考点三 模型应用
04.如图, 已知等腰 D在的CA延长线上,E在AC的延长线上, 连接BE,过点A作BE的垂线交BC于点F,垂足为O,连接DF并延长交BE于点K, 求BE的长度 .
专题十二 全等辅助线与模型进阶 (7)
——特殊角 与等腰直角三角形的构造
核心考点一 已有等腰直角三角形,利用 构造等腰直角三角形得手拉手
01.如图, 在等腰 中,
(1) 求证:
(2) 若BD=6, CD=2, 求四边形ABCD的面积.
核心考点二 利用45°构造等腰直角三角形,利用8字型构造旋转型全等
02.如图,在Rt△ABC中,∠A=90°.点D在AB边上,点E在AC边上,满足 若DE=1, BC=7, 则,
A. 2 B. 4
C. 5 D. 6
03.如图, 在四边形ABCD中, . 求证:
核心考点三 特殊角 角的处理
04. 如图, 在△ABC中, 于点D, BE平分. 且. 于点E,与CD相交于点F,H是边BC的中点,连接DH与BE相交于点G.若GE=3,则
核心考点四 等腰直角三角形的构造综合
05已知等腰 中,
(1) 如图1, 若 连DC, 求证:
(2)如图2,若点D在AB的延长线上,以DC为斜边作等腰 ,过直角顶点E作. 于F, 求证: 点F是AC的中点.
06. 已知A(a, 0), B(0, b), a,b满足 C为OB上一点,连AC, 作 且 连BD交x轴于点E(1, 0).
(1) 求点a, b的值; (2) 求点C的坐标;
(3) 在(2) 的前提下,点F是x轴上一个动点满足 请求出点F的坐标.
