第十三章轴对称 中档题专题提优(无答案)2024-2025学年人教版八年级数学上册
文档属性
| 名称 | 第十三章轴对称 中档题专题提优(无答案)2024-2025学年人教版八年级数学上册 |  | |
| 格式 | docx | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-18 17:12:10 | ||
图片预览


文档简介
第十三章 轴对称
专题一 轴对称和轴对称图形
核心考点一 轴对称的定义和性质
01.如图, 在△ABC中, 点D在BC边上, 将点D分别以AB, AC为对称轴, 画出对称点E, F, 并连接AE, AF. 根据图中标示的度数, 可求得∠EAF的大小为 ( )
A. 108° B. 115°
C. 122° D. 130°
核心考点二 坐标系内点的对称
02.已知点P(3, 2m-3) 关于x轴对称的点在第四象限, 则m的取值范围是 ( )
A. m>3 B. m<3
核心考点三 利用图形的折叠和对称求角度
03.如图, 在△ABC中, ∠BAC=90°, ∠B=50°, AD⊥BC, 垂足为D, △ADB与△ADB'关于直线AD对称, 点B 的对称点是点 B', 则∠CAB'的度数为( )
A. 10° B. 20°
C. 30° D. 40°
04.如图, 将一个直角三角形纸片(∠ACB=90°), 沿线段CD折叠, 使点 B落在点B 处,若 ,则∠ACD 的度数为( )
A. 30° B. 25°
C. 20° D. 15°
核心考点四 利用图形的折叠和对称求线段,周长或面积
05.如图, 在△ABC中, ∠C=90°, AC=BC, AD平分 交BC于D,. 于E,且AB=6cm, 则△DEB的周长为 ( )
A. 4cm B. 6cm
C. 8cm D. 10cm
06.在如图的三角形纸片中, AB=8cm, BC=6cm, AC=5cm,沿过点B的直线折叠这个三角形, 使点C落在AB上的点E处, 折痕为BD, 则△AED的周长为 ( )
A. 5cm B. 6cm
C. 7cm D. 8cm
B
核心考点五 通过数对称轴的个数,找轴对称图形的个数
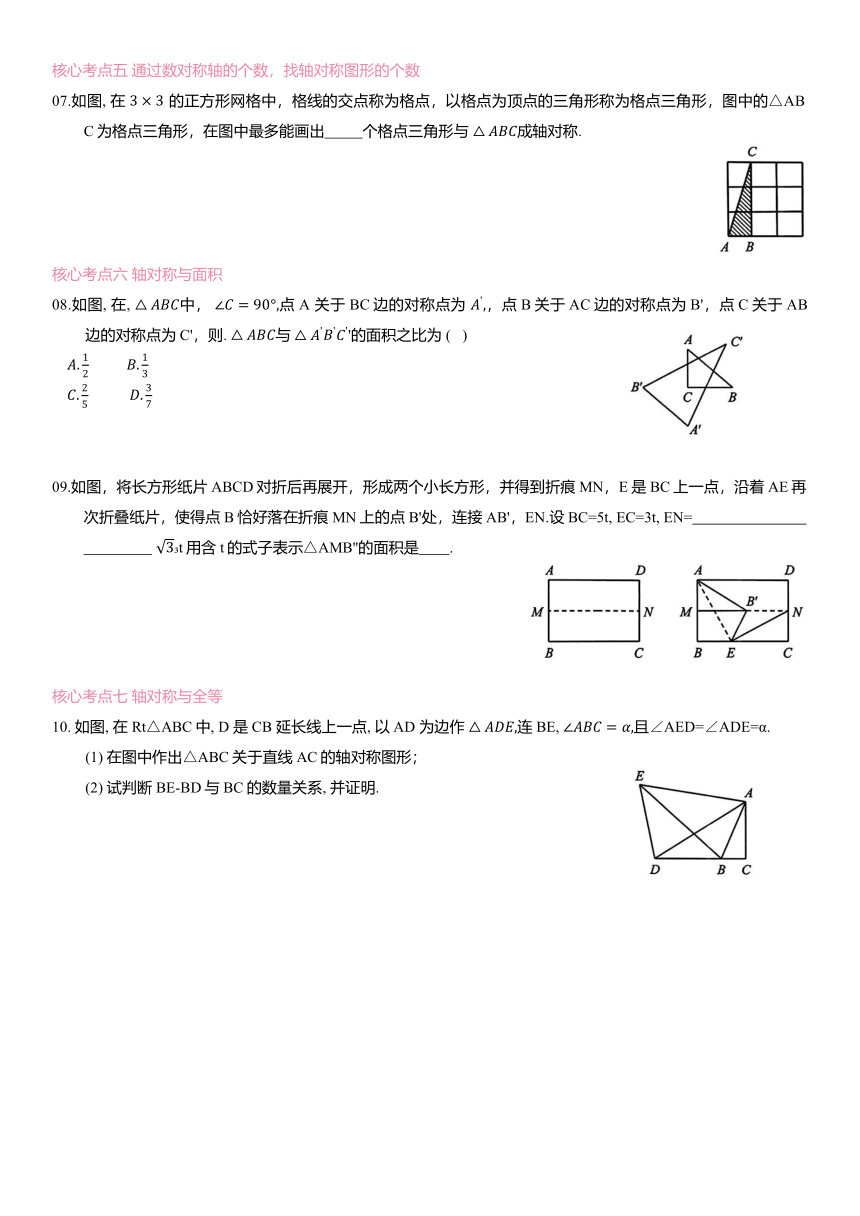
07.如图, 在 的正方形网格中,格线的交点称为格点,以格点为顶点的三角形称为格点三角形,图中的△ABC为格点三角形,在图中最多能画出 个格点三角形与 成轴对称.
核心考点六 轴对称与面积
08.如图, 在, 中, 点 A 关于 BC边的对称点为 ,点B关于AC边的对称点为B',点C关于AB边的对称点为C',则. 与 '的面积之比为 ( )
09.如图,将长方形纸片ABCD对折后再展开,形成两个小长方形,并得到折痕MN,E是BC上一点,沿着AE再次折叠纸片,使得点B恰好落在折痕MN上的点B'处,连接AB',EN.设BC=5t, EC=3t, EN= t用含t的式子表示△AMB''的面积是 .
核心考点七 轴对称与全等
10. 如图, 在 Rt△ABC中, D 是 CB 延长线上一点, 以AD 为边作 连 BE, 且∠AED=∠ADE=α.
(1) 在图中作出△ABC关于直线AC的轴对称图形;
(2) 试判断BE-BD与BC的数量关系, 并证明.
专题二 线段的垂直平分线及性质 (1) ——线段处理
核心考点一 利用线段垂直平分线的性质求线段长,周长
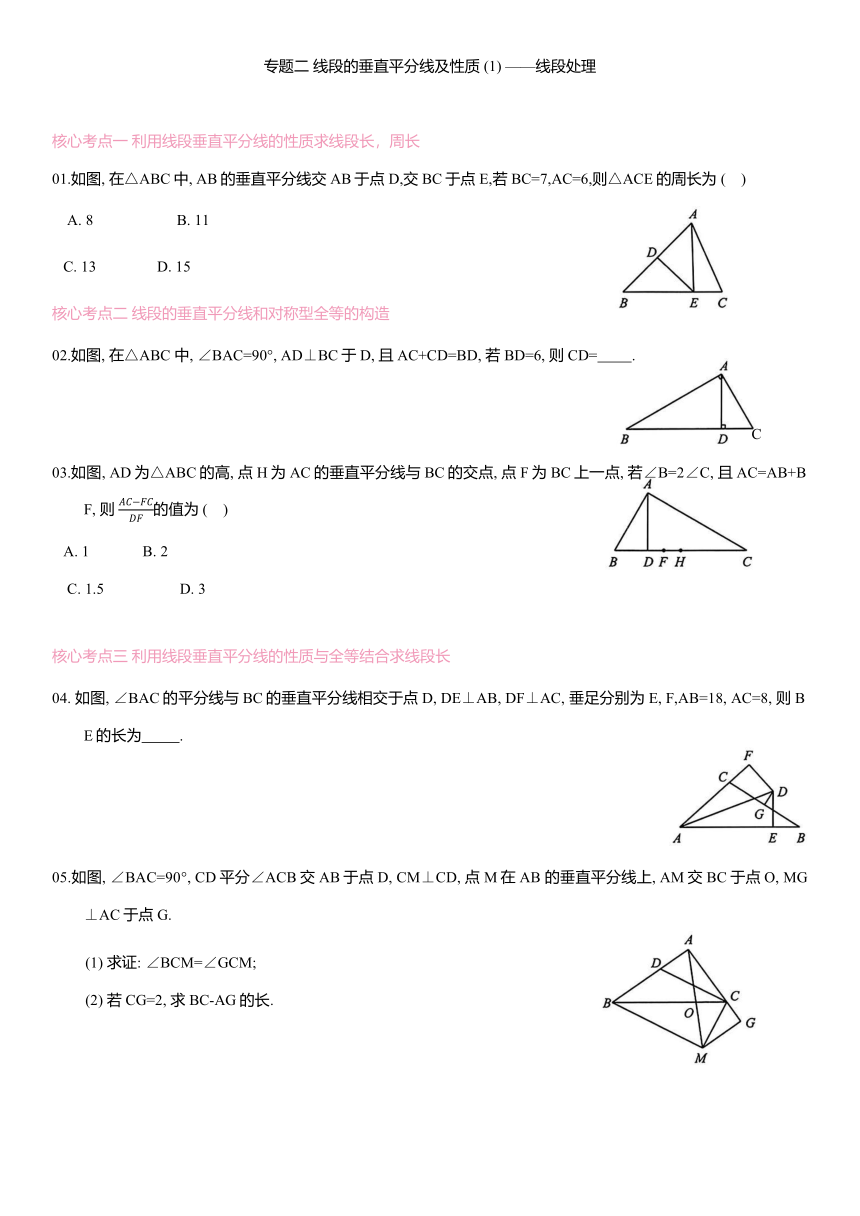
01.如图, 在△ABC中, AB的垂直平分线交AB于点D,交BC于点E,若BC=7,AC=6,则△ACE的周长为 ( )
A. 8 B. 11
C. 13 D. 15
核心考点二 线段的垂直平分线和对称型全等的构造
02.如图, 在△ABC 中, ∠BAC=90°, AD⊥BC于D, 且AC+CD=BD, 若BD=6, 则CD= .
C
03.如图, AD为△ABC的高, 点H为AC的垂直平分线与BC的交点, 点F为BC上一点, 若∠B=2∠C, 且AC=AB+BF, 则 的值为 ( )
A. 1 B. 2
C. 1.5 D. 3
核心考点三 利用线段垂直平分线的性质与全等结合求线段长
04. 如图, ∠BAC的平分线与BC的垂直平分线相交于点D, DE⊥AB, DF⊥AC, 垂足分别为E, F,AB=18, AC=8, 则BE的长为 .
05.如图, ∠BAC=90°, CD平分∠ACB交AB于点D, CM⊥CD, 点M在AB 的垂直平分线上, AM交BC于点O, MG⊥AC于点G.
(1) 求证: ∠BCM=∠GCM;
(2) 若CG=2, 求BC-AG的长.
专题三 线段的垂直平分线及性质 (2)——角度处理
核心考点一 利用垂直平分线求角度
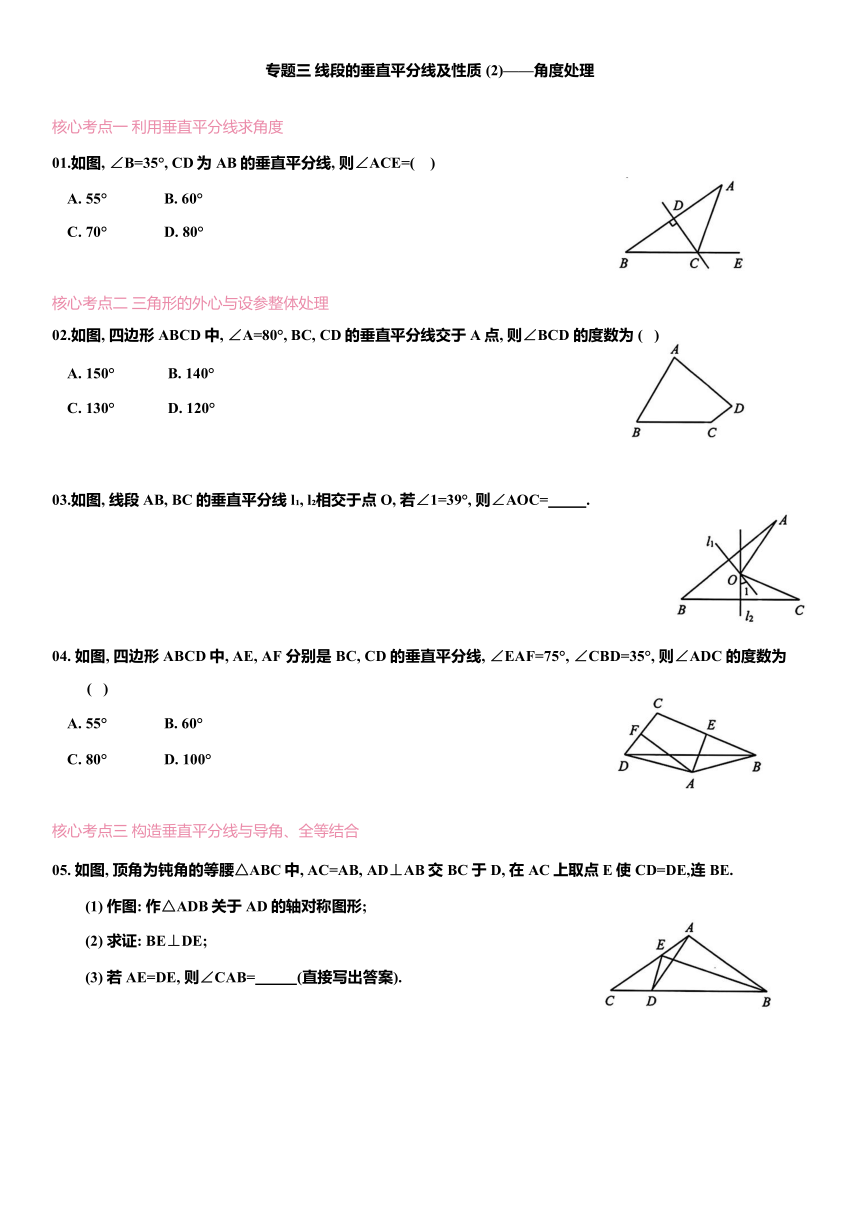
01.如图, ∠B=35°, CD为AB的垂直平分线, 则∠ACE=( )
A. 55° B. 60°
C. 70° D. 80°
核心考点二 三角形的外心与设参整体处理
02.如图, 四边形ABCD中, ∠A=80°, BC, CD的垂直平分线交于A点, 则∠BCD 的度数为 ( )
A. 150° B. 140°
C. 130° D. 120°
03.如图, 线段 AB, BC的垂直平分线l , l 相交于点 O, 若∠1=39°, 则∠AOC= .
04. 如图, 四边形ABCD中, AE, AF 分别是BC, CD的垂直平分线, ∠EAF=75°, ∠CBD=35°, 则∠ADC的度数为 ( )
A. 55° B. 60°
C. 80° D. 100°
核心考点三 构造垂直平分线与导角、全等结合
05. 如图, 顶角为钝角的等腰△ABC中, AC=AB, AD⊥AB交BC于D, 在AC上取点E使CD=DE,连BE.
(1) 作图: 作△ADB关于 AD的轴对称图形;
(2) 求证: BE⊥DE;
(3) 若AE=DE, 则∠CAB= (直接写出答案).
专题四 等腰三角形的性质和判定
01. 等腰三角形一腰上的高与另一腰所成的夹角为40°,,则顶角度数为 .
02. 如图, 在△ABC中, BO平分∠ABC, CO平分∠ACB, 过点O作. MN分别与AB, AC相交于点M, N, 若△ABC的周长为18, △AMN的周长为12, 则BC的长是 .
03. 如图, 在△ABC中, AB=AC, 点D, E, F分别在AB, BC, AC边上, 且
(1) 求证: △DEF是等腰三角形;
(2) 当∠A=40°时, 求∠DEF的大小.
04. 如图, 点P是△ABC内部一点, 且. 连接CP.
(1) 求证: ∠ACP=∠BCP;
(2) 若AB=3CP=3, 直接写出△APC的面积.
05. 在 中, AB=AC, BD平分∠ABC, 交AC于点D,
(1) 如图1, 求∠BAC的度数;
(2)如图2,E是AB的中点,连接ED并延长,交BC的延长线于点F,连接AF.求证:
06. 如图, 在 中, , 点E是AC的中点, 连接BE, 于点F, 交AB于D, CD=BE. 若, 则BD的长为( )
A. 2
07.如图, △ABC中, AB=AC, E在线段AC上, D在AB的延长线上, 连DE交BC于F, 过E作EG⊥BC于 G.
(1) 若∠A=50°, ∠D=30°, 求∠GEF的度数;
(2) 若 BD=CE, 求证: FG=BF+GC.
08. 如图, 在 中, D, E分别为AB, BC上的点, 且AE, CD交于点F, 若 ∠B=2∠FAC=2∠FCA, 求证: AD=CE.
C
09. 如图1, 在 中, 的平分线BD交边AC于点D.
(1) 求证: 为等腰三角形;
(2) 若 的平分线AE交边BC于点E,如图2,求证:
(3)若 外角的平分线AE交CB延长线于点E,请你探究(2)中的结论是否仍然成立 直接写出正确的结论.
专题五 设参导角求等腰三角形相关的角
01. 如图, 在△ABC中, AB=AC, 点D在AC上, 且BD=BC=AD, 则∠A的度数为 ( )
A. 30° B. 35°
C. 36° D. 40°
02如图, 在△ABC中, 点D在边BC上, BD=DC=AC, AE是 C的中线,∠B=35°,∠C=50°, ∠DAE的度数为 ( )
A. 30° B. 35°
C. 40° D. 50°
C
03. 如图, 在△ABC中, ∠B=∠C, 点 D 为BC边上一点, 点 E 在 AC 边上,∠ADE=∠AED=70°, ∠CDE=15°, 则∠BAD= ( )
A. 55° B. 40°
C. 30° D. 20°
04.如图, OA=OB=OC, ∠BOC=66°, 则∠BAC的度数是 .
05.如图, 已知 C的三条内角平分线相交于点I,三边的垂直平分线相交于点 O.若 则
C. 127° D. 132°
专题六 角平分线与平行线结合得等腰
方法:角平分线与平行线结合可得等腰三角形,三者之间,知二推一
核心考点一 认识模型
01. (1) 如图1, 中, BD平分∠ABC, CD平分∠ACB, 过点D作EF∥BC, 分别交AB, AC于 E,F两点,则图中共有 个等腰三角形,分别是 ;EF与BE,CF之间的关系是 ;
(2) 如图2, 点D在 外, 且BD平分∠ABC, CD平分△ABC的外角∠ACG, 过D点作DE∥BC, 分别交AB, AC于E, F两点, 则EF与BE, CF之间有何关系 写出你的结论,并加以证明;
(3) 如图3, 点D在△ABC外, BD, CD 分别平分△ABC的外角∠GBC和∠HCB, 过点D作DE∥BC, 分别交BG, CH于E, F两点, 直接写出EF与BE, CF之间存在的数量关系:
核心考点二 应用模型
02如图, 点O是 角平分线的交点,过点O作 分别与AB,AC相交于点M, N, 若. 则 的周长为 .
03.如图, 的 的外角平分线BD 与 的外角平分线CE交于点P,过点P作 交AC于点M,交BC于点N, 且. 则
A. 2 B. 3
C. 4 D. 5
专题七 倍角的处理策略(新热点)
01. 如图, 在△ABC中, 已知AD平分 ,则∠B和∠C的数量关系是 .
C
02.如图, CD是 的高,且. 若 则.
03.如图, 在△ABC中, , D 为边 BC上一点, 连接AD. 若∠ABC=2∠CAD, 则线段BD的长= .(用含a, b的式子表示)
04. 如图, 在四边形ABCD中, AC, BD相交于点E. 若E为BD的中点, CE=8, 则AB 的长为 .
C
05. 如图, △ABC中, ∠ABC=2∠C, BD平分. 于 F.求证: (1) ∠BAF=∠DAF+∠C: (2) AC=2BF.
专题八 分类讨论思想求等腰三角形的个数
01. 如图, 坐标平面内一点A(2, -1), O为原点, P是x轴上的一个动点, 如果以点P,O,A为顶点的三角形是等腰三角形,那么符合条件的动点P的个数为( )
A. 2 B. 3
C. 4 D. 5
02.如图,是一个5×5的正方形网格,网格中的每个小正方形的边长均为1. 点A和点B 在小正方形的顶点上. 点C 也在小正方形的顶点上,若 为等腰三角形,满足条件的C点的个数为 ( )个.
A. 9 B. 8
C. 7 D. 6
03.如图,在Rt△ABC中,以△ABC的一边为边画等腰三角形,使得它的第三个顶点在△ABC的其他边上,则可以画出的不同的等腰三角形的个数最多为 ( )
A. 7 B. 6
C. 5 D. 4
04.如图, B是直线l上的一点, 线段AB 与l的夹角为( 点C在l上,若以A,B,C为顶点的三角形是等腰三角形,则满足条件的点C共有 ( )
A. 2个 B. 3个
C. 2个或4个 D. 3个或4个
l
专题九 巧用“三线合一”
核心考点一 直接利用三线合一得二倍角 (或导角)
01. 如图, 在△ABC中, AB=AC, CH⊥AB于点H. 求证: ∠A=2∠BCH.
核心考点二 直接利用三线合一与面积法求线段长
02.如图, 在△ABC中, AB=AC, AD⊥BC于点D, DE⊥AB于点E, BF⊥AC于点F,DE=3cm, 则BF= cm.
核心考点三 放垂构造三线合一证明线段关系
03. 如图, 已知在△ABC中, AB=AC, 点D, E在边BC上, 且AD=AE. 证明: BD=CE.
核心考点四 连接等腰三角形的顶角定点和底边中点构造三线合一证明全等
04. 如图, Rt△ABC中, AC=BC, ∠C=90°, D为AB边的中点, ∠EDF=90°, E, F分别在AC, BC上.
(1) 求证: DE=DF; (2) 求证:
核心考点五 放垂构造三线合一,导角证明全等
05. 如图, 则 的面积为 .
06. 如图, 在四边形ABCD中, 若
(1) 求证: ∠ACB=2∠ABD; (2) 求△ABD的面积.
07. 如图, D, E, F是△ABC边上的点, EF与AD交于点G, ∠C=∠AGF=45°, 求△AFG的面积.
C
核心考点六 三线合一,夹半角结合
08. 在 中, . , 分别交直线AB, AC于点M, N.
(1) 如图1, 当 时,求证:
(2) 如图2, 当( 时,求证:
(3) 当 时,旋转∠MON至图3位置,请你直接写出线段BM,MN,AN之间的数量关系.
专题十 无刻度直尺格点作图(2) ——轴对称与最值(新热点)
核心考点一 利用三线合一及内心的性质作三角形的内角平分线
01.仅用无刻度的直尺作图, 保留作图痕迹: 如图, BD是△ABC的角平分线, 作△ABC的内角∠BCA的角平分线CE.
核心考点二 构造等腰直角三角形或者正方形,作线段的垂直平分线
02. 如图,点A,B在格点上,仅用无刻度的直尺在给定网格中按要求画图.
(1) 将线段AB绕A逆时针旋转90°得线段AC; (2) 画AB的垂直平分线.
03.如图,在10×10的正方形网格中,点A,B,C都在格点上,仅用无刻度的直尺在给定网格中完成画图,画图过程用虚线表示. 在图中画出BC边的垂直平分线.
核心考点三 利用三线合一及内心的性质作三角形的内角平分线
04如图, 点A, B, C均在格点上, 只用无刻度的直尺, 按要求作图:
(1) 如图1, AB=5, 作出∠BAC的角平分线AP;
(2) 如图2, BD是△ABC的角平分线, 作∠BCA 的角平分线CE;
(3)如图3, 点D在AC上, AB=5, 在AB上画点P, 使AP=AD.
05.如图,△ABC的顶点都在小正方形的顶点上,AB=5. 仅用无刻度的直尺作图,画图过程用虚线,画图结果用实线.
(1)如图1, 在格点上找点D, 连接AD, 使AD=5且AD∥BC, 再在AC上找点E, 使BE角平分∠ABC;
(2)如图2,在格点上找点F,使AF⊥AB且AF=AB,再在直线AC上找一点P,使∠APB=∠ABC.
核心考点四 构对称型全等作线段的垂直平分线
06.请仅用无刻度的直尺完成下列作图,不要求写作法,保留作图痕迹.
(1) 如图1, 四边形ABCD中, AB=AD, ∠B=∠D, BC=DC, 请画出四边形ABCD的对称轴;
(2) 如图2, 四边形ABCD中,. ,请画出BC边的垂直平分线m;
(3) 如图3,在一个5×6的方格图中有一个格点△ABC(顶点A,B,C均在格点上),请画出AC边上的高BH.
核心考点五 整体平移法
07.如图是由边长为1的小正方形构成的网格, 的顶点在格点上.
(1)如图1,点F是AC与网格线的交点,请在BC上作一点H,使
(2)如图2,直线a和直线b在网格线上,点A和点H在两条直线的两侧,请在直线a上作一点M, 过点M作MN⊥b于点N, 连接HN, 使得AM+MN+NH的最小.
专题十一 无刻度直尺格点作图(3)——轴对称与最值综合训练
01如图, △ABC的三个顶点A, B, C均在格点上, 已知AB=5, 请只用无刻度的直尺,在给定的网格中按要求画图,保留作图痕迹.
(1) △ABC面积为 ;
(2) 画出AB边上高CH;
(3) 作出∠BAC的角平分线AP.
02.如图,△ABC的三个顶点都是格点,其中AB=5. 仅用无刻度的直尺在给定网格中完成画图,画图过程用虚线表示,画图结果用实线表示.
(1) 在图1中, 先画边AB上的中线CD; 再画∠BAC的平分线AE;
(2)在图2中, 先画CF⊥AB于点F; M是边AB上一点, 再画点M关于直线BC的对称点N.
03如图, 在7×7的正方形网格中, 点A, B, C都在格点上, 点D是AB与网格线的交点,且AB=5,仅用无刻度的直尺在给定网格中完成画图,画图过程用虚线表示.
(1) 作AB边上高CE;
(2) 画出点D关于AC的对称点 F;
(3) 在AB上画点M, 使BM=BC;
(4) 在△ABC内画点P, 使
04.如图,边长为1的小正方形构成的6×6网格中,每个小正方形的顶点称为格点. AD是△ABC的角平分线, 其中A, B, D为格点.
(1) 画出AB的中点M;
(2) 在AC上画点N, 使ND∥AB;
(3) 画点 B 关于 AD的对称点 P;
(4) 若△QAB 是等腰三角形,直接写出该网格中满足条件的格点Q的个数.
专题十二 利用对称轴的个数求轴对称图形的个数
01.如图,在3×3的正方形格纸中,格线的交点称为格点,以格点为顶点的三角形称为格点三角形,图中△ABC是一个格点三角形. 在这个3×3的正方形格纸中,与 成轴对称的格点三角形最多有 ( )
A. 3个 B. 4个
C. 5个 D. 6个
02. 如图,是一个3×4的网格(由12个小正方形组成,虚线交点称之格点) 图中有一个三角形,三个顶点都在格点上,在网格中可以画出( )个与此三角形关于某直线对称的格点三角形.
A. 6 B. 7
C. 8 D. 9
03.如图,在4×4的正方形网格中,与△ABC关于某条直线对称的格点三角形(顶点在格线交点的三角形) 共有 个.
04. 在如图所示 的正方形网格中,有三个小方格被涂上了阴影,请在图中再选择两个空白的小正方形并涂成阴影,使得图中的阴影部分成为轴对称图形,共有 ( )不同的填涂方法.
A. 4种 B. 5种
C. 6种 D. 7种
专题十三 等边三角形(1) ——性质与判定
核心考点一 等边三角形的性质
01.如图, 正△ABC中, 点D, E分别为BC, CA上的两点, 且BD=CE, 连接AD, BE交于点F, 则∠FAE+∠AEF的度数是 .
核心考点二 等边三角形的判定——两边等+有一角为60°
02.如图,将△ABC绕A 点逆时针旋转60°得到△ADE,连接DE,若 则 的度数是( )
A. 110° B. 120°
C. 130° D. 150°
03.已知∠AOB=30°, 点P在∠AOB的内部, P 与P关于OA对称, P 与P关于OB对称, 则△P OP 是( )
A. 含 30°角的直角三角形 B. 顶角是30°的等腰三角形
C. 等腰直角三角形 D. 等边三角形
核心考点三 等边三角形的判定——两角为60°
04. 如图,一个六边形的每个内角都是 120°,连续四边的长依次是2.7,3,5,2,则该六边形的周长是 .
05.如图, Rt△ABC中, ∠ACB=90°, CA=CB, ∠BAD=∠ADE=60°, DE=3, AB=10,CE平分∠ACB, DE与CE相交于点E, 则AD的长为 ( )
A. 4 B. 13
C. 6.5 D. 7
核心考点四 等边三角形与旋转全等
06.如图, △ABC和△ADE都是等边三角形, 点D在BC上, DE与AC交于点F. 若AB=5, BD=3, 则
核心考点五 等边三角形与 直角三角形综合
07. 如图, 中,BD是AC边上的中线, 于点B, ∠ABC=120°, 求证: AB=2BC.
08.如图, 在等边 中, AE=CD, AD, BE交于P点, BQ⊥AD 于Q.
(1) 求证: ( 2) 连PC, 若BP⊥PC, 求 的值.
核心考点六 作平行 (或截长补短) 构造等边三角形
09.如图, 在等边△ABC中, D是AB上一点, E是BC延长线上一点, AD=CE, DE交AC于点 F.
(1) 求证: DF=EF;
(2) 过点D作DH⊥AC于点H, 求 的值.
10. 在等边 中,点D和点E分别在边AB,BC上,以DE为边向右作等边 连接CF.
(1) 如图1, 当点D和点A重合时, 求. 的大小;
(2) 如图2, 点D是边AB 的中点, 求证:
专题十四 等边三角形(2)——特殊角( 与等边三角形的构造
01. 如图, △ABC为等边三角形, ∠ADC=60°. 求证:
02. 如图, △ABC为等边三角形, ∠BDC=120°. 求证: AD=BD+CD.
03. 如图,在 中,AB=AC, 点D是 外的一点,且 求证:
04.如图, 在等边△ABC中, 点D为边BC上一点, 交AD的延长线于点 F.
(1) 求 的度数;
(2) 若 BE=10, AF=15, 求AE的长.
05.如图, 都是等边三角形.
(1) 求证:
(2) 设BE, DC交于M, 连AM, 求 的值.
06.(1) 探究: 如图1, △ABC和△ADE都是等边三角形, 点D在边BC上.
①求 的大小;
②直接写出线段CD,CE,AC之间的数量关系;
(2)应用: 如图2, 在四边形 ABCD 中, AB=BC, ∠ABC=60°, P 是四边形ABCD 内一点, 且 求证:
(3)拓展:如图.3,在平面直角坐标系中,点A的坐标为(-4,0) ,点B是y轴上一个动点,以AB为边在AB的下方作等边△ABC,求OC的最小值.
专题十五 直角三角形中30°角所对的直角边等于斜边的一半
核心考点一 直接运用定理
01.如图, Rt△ABC中, ∠ACB=90°, CD⊥AB, 若∠A=30°, BD=1, 则AD的长为 ·
02. 如图, 在△ABC中, AB=AC, ∠B=30°, AD⊥AB交BC于点D, AD=3, 则BC的长是 ( )
A. 8 B. 9
C. 10 D. 11
核心考点二 先构造图形,再运用定理
03. 如图, 点C在△ABD的边BD上,AC=AB,若AD=8, CD=3,∠D=60°, 则BC的长是 .
04.如图, 已知∠AOB=30°, P是∠AOB平分线上一点, CP∥OB, 交OA于点C, PD⊥OB, 垂足为点D, 且PC=4, 则PD的长是 ( )
A. 1 B. 2
C. 4 D. 8
05. 如图, 在Rt△ABC中, ∠C=90°, AB的垂直平分线DE交BC于点E, 若 则BE的长度是 .
06.如图, △ABC中, BC=2AC, ∠DBC=∠ACB=120°, BD=BC, CD交边AB于点E.
(1) 求∠ACE的度数;
(2) 求证: DE=3CE.
07. 已知 为等腰三角形,BC边上的高恰好等于BC边长的一半,则∠BAC的大小为 .
08.如图, 在. 中, ∠C=30°, 点D是AC的中点,. 交BC于E, 点O在DE上, OA=OB, OD=2, OE=4, 则BE的长为 .
09如图, 在 中, CM平分 交AB于点M,过点M作 BC交AC于点N, 且MN平分∠AMC, 若AN=1, 则BC的长为 .
C
10.如图, △ABC和 是一副直角三角板,其中 , 延长 AD,CB交于点E, 延长AB至F, 使BF=2AB, 那么∠F的度数是 .
核心考点三 构造全等,再结合定理解题
11.如图, 在 中, , 点D, E, F分别为边AC, AB, CB上的点,且 为等边三角形,若 则 的值为 .
B
专题一 轴对称和轴对称图形
核心考点一 轴对称的定义和性质
01.如图, 在△ABC中, 点D在BC边上, 将点D分别以AB, AC为对称轴, 画出对称点E, F, 并连接AE, AF. 根据图中标示的度数, 可求得∠EAF的大小为 ( )
A. 108° B. 115°
C. 122° D. 130°
核心考点二 坐标系内点的对称
02.已知点P(3, 2m-3) 关于x轴对称的点在第四象限, 则m的取值范围是 ( )
A. m>3 B. m<3
核心考点三 利用图形的折叠和对称求角度
03.如图, 在△ABC中, ∠BAC=90°, ∠B=50°, AD⊥BC, 垂足为D, △ADB与△ADB'关于直线AD对称, 点B 的对称点是点 B', 则∠CAB'的度数为( )
A. 10° B. 20°
C. 30° D. 40°
04.如图, 将一个直角三角形纸片(∠ACB=90°), 沿线段CD折叠, 使点 B落在点B 处,若 ,则∠ACD 的度数为( )
A. 30° B. 25°
C. 20° D. 15°
核心考点四 利用图形的折叠和对称求线段,周长或面积
05.如图, 在△ABC中, ∠C=90°, AC=BC, AD平分 交BC于D,. 于E,且AB=6cm, 则△DEB的周长为 ( )
A. 4cm B. 6cm
C. 8cm D. 10cm
06.在如图的三角形纸片中, AB=8cm, BC=6cm, AC=5cm,沿过点B的直线折叠这个三角形, 使点C落在AB上的点E处, 折痕为BD, 则△AED的周长为 ( )
A. 5cm B. 6cm
C. 7cm D. 8cm
B
核心考点五 通过数对称轴的个数,找轴对称图形的个数
07.如图, 在 的正方形网格中,格线的交点称为格点,以格点为顶点的三角形称为格点三角形,图中的△ABC为格点三角形,在图中最多能画出 个格点三角形与 成轴对称.
核心考点六 轴对称与面积
08.如图, 在, 中, 点 A 关于 BC边的对称点为 ,点B关于AC边的对称点为B',点C关于AB边的对称点为C',则. 与 '的面积之比为 ( )
09.如图,将长方形纸片ABCD对折后再展开,形成两个小长方形,并得到折痕MN,E是BC上一点,沿着AE再次折叠纸片,使得点B恰好落在折痕MN上的点B'处,连接AB',EN.设BC=5t, EC=3t, EN= t用含t的式子表示△AMB''的面积是 .
核心考点七 轴对称与全等
10. 如图, 在 Rt△ABC中, D 是 CB 延长线上一点, 以AD 为边作 连 BE, 且∠AED=∠ADE=α.
(1) 在图中作出△ABC关于直线AC的轴对称图形;
(2) 试判断BE-BD与BC的数量关系, 并证明.
专题二 线段的垂直平分线及性质 (1) ——线段处理
核心考点一 利用线段垂直平分线的性质求线段长,周长
01.如图, 在△ABC中, AB的垂直平分线交AB于点D,交BC于点E,若BC=7,AC=6,则△ACE的周长为 ( )
A. 8 B. 11
C. 13 D. 15
核心考点二 线段的垂直平分线和对称型全等的构造
02.如图, 在△ABC 中, ∠BAC=90°, AD⊥BC于D, 且AC+CD=BD, 若BD=6, 则CD= .
C
03.如图, AD为△ABC的高, 点H为AC的垂直平分线与BC的交点, 点F为BC上一点, 若∠B=2∠C, 且AC=AB+BF, 则 的值为 ( )
A. 1 B. 2
C. 1.5 D. 3
核心考点三 利用线段垂直平分线的性质与全等结合求线段长
04. 如图, ∠BAC的平分线与BC的垂直平分线相交于点D, DE⊥AB, DF⊥AC, 垂足分别为E, F,AB=18, AC=8, 则BE的长为 .
05.如图, ∠BAC=90°, CD平分∠ACB交AB于点D, CM⊥CD, 点M在AB 的垂直平分线上, AM交BC于点O, MG⊥AC于点G.
(1) 求证: ∠BCM=∠GCM;
(2) 若CG=2, 求BC-AG的长.
专题三 线段的垂直平分线及性质 (2)——角度处理
核心考点一 利用垂直平分线求角度
01.如图, ∠B=35°, CD为AB的垂直平分线, 则∠ACE=( )
A. 55° B. 60°
C. 70° D. 80°
核心考点二 三角形的外心与设参整体处理
02.如图, 四边形ABCD中, ∠A=80°, BC, CD的垂直平分线交于A点, 则∠BCD 的度数为 ( )
A. 150° B. 140°
C. 130° D. 120°
03.如图, 线段 AB, BC的垂直平分线l , l 相交于点 O, 若∠1=39°, 则∠AOC= .
04. 如图, 四边形ABCD中, AE, AF 分别是BC, CD的垂直平分线, ∠EAF=75°, ∠CBD=35°, 则∠ADC的度数为 ( )
A. 55° B. 60°
C. 80° D. 100°
核心考点三 构造垂直平分线与导角、全等结合
05. 如图, 顶角为钝角的等腰△ABC中, AC=AB, AD⊥AB交BC于D, 在AC上取点E使CD=DE,连BE.
(1) 作图: 作△ADB关于 AD的轴对称图形;
(2) 求证: BE⊥DE;
(3) 若AE=DE, 则∠CAB= (直接写出答案).
专题四 等腰三角形的性质和判定
01. 等腰三角形一腰上的高与另一腰所成的夹角为40°,,则顶角度数为 .
02. 如图, 在△ABC中, BO平分∠ABC, CO平分∠ACB, 过点O作. MN分别与AB, AC相交于点M, N, 若△ABC的周长为18, △AMN的周长为12, 则BC的长是 .
03. 如图, 在△ABC中, AB=AC, 点D, E, F分别在AB, BC, AC边上, 且
(1) 求证: △DEF是等腰三角形;
(2) 当∠A=40°时, 求∠DEF的大小.
04. 如图, 点P是△ABC内部一点, 且. 连接CP.
(1) 求证: ∠ACP=∠BCP;
(2) 若AB=3CP=3, 直接写出△APC的面积.
05. 在 中, AB=AC, BD平分∠ABC, 交AC于点D,
(1) 如图1, 求∠BAC的度数;
(2)如图2,E是AB的中点,连接ED并延长,交BC的延长线于点F,连接AF.求证:
06. 如图, 在 中, , 点E是AC的中点, 连接BE, 于点F, 交AB于D, CD=BE. 若, 则BD的长为( )
A. 2
07.如图, △ABC中, AB=AC, E在线段AC上, D在AB的延长线上, 连DE交BC于F, 过E作EG⊥BC于 G.
(1) 若∠A=50°, ∠D=30°, 求∠GEF的度数;
(2) 若 BD=CE, 求证: FG=BF+GC.
08. 如图, 在 中, D, E分别为AB, BC上的点, 且AE, CD交于点F, 若 ∠B=2∠FAC=2∠FCA, 求证: AD=CE.
C
09. 如图1, 在 中, 的平分线BD交边AC于点D.
(1) 求证: 为等腰三角形;
(2) 若 的平分线AE交边BC于点E,如图2,求证:
(3)若 外角的平分线AE交CB延长线于点E,请你探究(2)中的结论是否仍然成立 直接写出正确的结论.
专题五 设参导角求等腰三角形相关的角
01. 如图, 在△ABC中, AB=AC, 点D在AC上, 且BD=BC=AD, 则∠A的度数为 ( )
A. 30° B. 35°
C. 36° D. 40°
02如图, 在△ABC中, 点D在边BC上, BD=DC=AC, AE是 C的中线,∠B=35°,∠C=50°, ∠DAE的度数为 ( )
A. 30° B. 35°
C. 40° D. 50°
C
03. 如图, 在△ABC中, ∠B=∠C, 点 D 为BC边上一点, 点 E 在 AC 边上,∠ADE=∠AED=70°, ∠CDE=15°, 则∠BAD= ( )
A. 55° B. 40°
C. 30° D. 20°
04.如图, OA=OB=OC, ∠BOC=66°, 则∠BAC的度数是 .
05.如图, 已知 C的三条内角平分线相交于点I,三边的垂直平分线相交于点 O.若 则
C. 127° D. 132°
专题六 角平分线与平行线结合得等腰
方法:角平分线与平行线结合可得等腰三角形,三者之间,知二推一
核心考点一 认识模型
01. (1) 如图1, 中, BD平分∠ABC, CD平分∠ACB, 过点D作EF∥BC, 分别交AB, AC于 E,F两点,则图中共有 个等腰三角形,分别是 ;EF与BE,CF之间的关系是 ;
(2) 如图2, 点D在 外, 且BD平分∠ABC, CD平分△ABC的外角∠ACG, 过D点作DE∥BC, 分别交AB, AC于E, F两点, 则EF与BE, CF之间有何关系 写出你的结论,并加以证明;
(3) 如图3, 点D在△ABC外, BD, CD 分别平分△ABC的外角∠GBC和∠HCB, 过点D作DE∥BC, 分别交BG, CH于E, F两点, 直接写出EF与BE, CF之间存在的数量关系:
核心考点二 应用模型
02如图, 点O是 角平分线的交点,过点O作 分别与AB,AC相交于点M, N, 若. 则 的周长为 .
03.如图, 的 的外角平分线BD 与 的外角平分线CE交于点P,过点P作 交AC于点M,交BC于点N, 且. 则
A. 2 B. 3
C. 4 D. 5
专题七 倍角的处理策略(新热点)
01. 如图, 在△ABC中, 已知AD平分 ,则∠B和∠C的数量关系是 .
C
02.如图, CD是 的高,且. 若 则.
03.如图, 在△ABC中, , D 为边 BC上一点, 连接AD. 若∠ABC=2∠CAD, 则线段BD的长= .(用含a, b的式子表示)
04. 如图, 在四边形ABCD中, AC, BD相交于点E. 若E为BD的中点, CE=8, 则AB 的长为 .
C
05. 如图, △ABC中, ∠ABC=2∠C, BD平分. 于 F.求证: (1) ∠BAF=∠DAF+∠C: (2) AC=2BF.
专题八 分类讨论思想求等腰三角形的个数
01. 如图, 坐标平面内一点A(2, -1), O为原点, P是x轴上的一个动点, 如果以点P,O,A为顶点的三角形是等腰三角形,那么符合条件的动点P的个数为( )
A. 2 B. 3
C. 4 D. 5
02.如图,是一个5×5的正方形网格,网格中的每个小正方形的边长均为1. 点A和点B 在小正方形的顶点上. 点C 也在小正方形的顶点上,若 为等腰三角形,满足条件的C点的个数为 ( )个.
A. 9 B. 8
C. 7 D. 6
03.如图,在Rt△ABC中,以△ABC的一边为边画等腰三角形,使得它的第三个顶点在△ABC的其他边上,则可以画出的不同的等腰三角形的个数最多为 ( )
A. 7 B. 6
C. 5 D. 4
04.如图, B是直线l上的一点, 线段AB 与l的夹角为( 点C在l上,若以A,B,C为顶点的三角形是等腰三角形,则满足条件的点C共有 ( )
A. 2个 B. 3个
C. 2个或4个 D. 3个或4个
l
专题九 巧用“三线合一”
核心考点一 直接利用三线合一得二倍角 (或导角)
01. 如图, 在△ABC中, AB=AC, CH⊥AB于点H. 求证: ∠A=2∠BCH.
核心考点二 直接利用三线合一与面积法求线段长
02.如图, 在△ABC中, AB=AC, AD⊥BC于点D, DE⊥AB于点E, BF⊥AC于点F,DE=3cm, 则BF= cm.
核心考点三 放垂构造三线合一证明线段关系
03. 如图, 已知在△ABC中, AB=AC, 点D, E在边BC上, 且AD=AE. 证明: BD=CE.
核心考点四 连接等腰三角形的顶角定点和底边中点构造三线合一证明全等
04. 如图, Rt△ABC中, AC=BC, ∠C=90°, D为AB边的中点, ∠EDF=90°, E, F分别在AC, BC上.
(1) 求证: DE=DF; (2) 求证:
核心考点五 放垂构造三线合一,导角证明全等
05. 如图, 则 的面积为 .
06. 如图, 在四边形ABCD中, 若
(1) 求证: ∠ACB=2∠ABD; (2) 求△ABD的面积.
07. 如图, D, E, F是△ABC边上的点, EF与AD交于点G, ∠C=∠AGF=45°, 求△AFG的面积.
C
核心考点六 三线合一,夹半角结合
08. 在 中, . , 分别交直线AB, AC于点M, N.
(1) 如图1, 当 时,求证:
(2) 如图2, 当( 时,求证:
(3) 当 时,旋转∠MON至图3位置,请你直接写出线段BM,MN,AN之间的数量关系.
专题十 无刻度直尺格点作图(2) ——轴对称与最值(新热点)
核心考点一 利用三线合一及内心的性质作三角形的内角平分线
01.仅用无刻度的直尺作图, 保留作图痕迹: 如图, BD是△ABC的角平分线, 作△ABC的内角∠BCA的角平分线CE.
核心考点二 构造等腰直角三角形或者正方形,作线段的垂直平分线
02. 如图,点A,B在格点上,仅用无刻度的直尺在给定网格中按要求画图.
(1) 将线段AB绕A逆时针旋转90°得线段AC; (2) 画AB的垂直平分线.
03.如图,在10×10的正方形网格中,点A,B,C都在格点上,仅用无刻度的直尺在给定网格中完成画图,画图过程用虚线表示. 在图中画出BC边的垂直平分线.
核心考点三 利用三线合一及内心的性质作三角形的内角平分线
04如图, 点A, B, C均在格点上, 只用无刻度的直尺, 按要求作图:
(1) 如图1, AB=5, 作出∠BAC的角平分线AP;
(2) 如图2, BD是△ABC的角平分线, 作∠BCA 的角平分线CE;
(3)如图3, 点D在AC上, AB=5, 在AB上画点P, 使AP=AD.
05.如图,△ABC的顶点都在小正方形的顶点上,AB=5. 仅用无刻度的直尺作图,画图过程用虚线,画图结果用实线.
(1)如图1, 在格点上找点D, 连接AD, 使AD=5且AD∥BC, 再在AC上找点E, 使BE角平分∠ABC;
(2)如图2,在格点上找点F,使AF⊥AB且AF=AB,再在直线AC上找一点P,使∠APB=∠ABC.
核心考点四 构对称型全等作线段的垂直平分线
06.请仅用无刻度的直尺完成下列作图,不要求写作法,保留作图痕迹.
(1) 如图1, 四边形ABCD中, AB=AD, ∠B=∠D, BC=DC, 请画出四边形ABCD的对称轴;
(2) 如图2, 四边形ABCD中,. ,请画出BC边的垂直平分线m;
(3) 如图3,在一个5×6的方格图中有一个格点△ABC(顶点A,B,C均在格点上),请画出AC边上的高BH.
核心考点五 整体平移法
07.如图是由边长为1的小正方形构成的网格, 的顶点在格点上.
(1)如图1,点F是AC与网格线的交点,请在BC上作一点H,使
(2)如图2,直线a和直线b在网格线上,点A和点H在两条直线的两侧,请在直线a上作一点M, 过点M作MN⊥b于点N, 连接HN, 使得AM+MN+NH的最小.
专题十一 无刻度直尺格点作图(3)——轴对称与最值综合训练
01如图, △ABC的三个顶点A, B, C均在格点上, 已知AB=5, 请只用无刻度的直尺,在给定的网格中按要求画图,保留作图痕迹.
(1) △ABC面积为 ;
(2) 画出AB边上高CH;
(3) 作出∠BAC的角平分线AP.
02.如图,△ABC的三个顶点都是格点,其中AB=5. 仅用无刻度的直尺在给定网格中完成画图,画图过程用虚线表示,画图结果用实线表示.
(1) 在图1中, 先画边AB上的中线CD; 再画∠BAC的平分线AE;
(2)在图2中, 先画CF⊥AB于点F; M是边AB上一点, 再画点M关于直线BC的对称点N.
03如图, 在7×7的正方形网格中, 点A, B, C都在格点上, 点D是AB与网格线的交点,且AB=5,仅用无刻度的直尺在给定网格中完成画图,画图过程用虚线表示.
(1) 作AB边上高CE;
(2) 画出点D关于AC的对称点 F;
(3) 在AB上画点M, 使BM=BC;
(4) 在△ABC内画点P, 使
04.如图,边长为1的小正方形构成的6×6网格中,每个小正方形的顶点称为格点. AD是△ABC的角平分线, 其中A, B, D为格点.
(1) 画出AB的中点M;
(2) 在AC上画点N, 使ND∥AB;
(3) 画点 B 关于 AD的对称点 P;
(4) 若△QAB 是等腰三角形,直接写出该网格中满足条件的格点Q的个数.
专题十二 利用对称轴的个数求轴对称图形的个数
01.如图,在3×3的正方形格纸中,格线的交点称为格点,以格点为顶点的三角形称为格点三角形,图中△ABC是一个格点三角形. 在这个3×3的正方形格纸中,与 成轴对称的格点三角形最多有 ( )
A. 3个 B. 4个
C. 5个 D. 6个
02. 如图,是一个3×4的网格(由12个小正方形组成,虚线交点称之格点) 图中有一个三角形,三个顶点都在格点上,在网格中可以画出( )个与此三角形关于某直线对称的格点三角形.
A. 6 B. 7
C. 8 D. 9
03.如图,在4×4的正方形网格中,与△ABC关于某条直线对称的格点三角形(顶点在格线交点的三角形) 共有 个.
04. 在如图所示 的正方形网格中,有三个小方格被涂上了阴影,请在图中再选择两个空白的小正方形并涂成阴影,使得图中的阴影部分成为轴对称图形,共有 ( )不同的填涂方法.
A. 4种 B. 5种
C. 6种 D. 7种
专题十三 等边三角形(1) ——性质与判定
核心考点一 等边三角形的性质
01.如图, 正△ABC中, 点D, E分别为BC, CA上的两点, 且BD=CE, 连接AD, BE交于点F, 则∠FAE+∠AEF的度数是 .
核心考点二 等边三角形的判定——两边等+有一角为60°
02.如图,将△ABC绕A 点逆时针旋转60°得到△ADE,连接DE,若 则 的度数是( )
A. 110° B. 120°
C. 130° D. 150°
03.已知∠AOB=30°, 点P在∠AOB的内部, P 与P关于OA对称, P 与P关于OB对称, 则△P OP 是( )
A. 含 30°角的直角三角形 B. 顶角是30°的等腰三角形
C. 等腰直角三角形 D. 等边三角形
核心考点三 等边三角形的判定——两角为60°
04. 如图,一个六边形的每个内角都是 120°,连续四边的长依次是2.7,3,5,2,则该六边形的周长是 .
05.如图, Rt△ABC中, ∠ACB=90°, CA=CB, ∠BAD=∠ADE=60°, DE=3, AB=10,CE平分∠ACB, DE与CE相交于点E, 则AD的长为 ( )
A. 4 B. 13
C. 6.5 D. 7
核心考点四 等边三角形与旋转全等
06.如图, △ABC和△ADE都是等边三角形, 点D在BC上, DE与AC交于点F. 若AB=5, BD=3, 则
核心考点五 等边三角形与 直角三角形综合
07. 如图, 中,BD是AC边上的中线, 于点B, ∠ABC=120°, 求证: AB=2BC.
08.如图, 在等边 中, AE=CD, AD, BE交于P点, BQ⊥AD 于Q.
(1) 求证: ( 2) 连PC, 若BP⊥PC, 求 的值.
核心考点六 作平行 (或截长补短) 构造等边三角形
09.如图, 在等边△ABC中, D是AB上一点, E是BC延长线上一点, AD=CE, DE交AC于点 F.
(1) 求证: DF=EF;
(2) 过点D作DH⊥AC于点H, 求 的值.
10. 在等边 中,点D和点E分别在边AB,BC上,以DE为边向右作等边 连接CF.
(1) 如图1, 当点D和点A重合时, 求. 的大小;
(2) 如图2, 点D是边AB 的中点, 求证:
专题十四 等边三角形(2)——特殊角( 与等边三角形的构造
01. 如图, △ABC为等边三角形, ∠ADC=60°. 求证:
02. 如图, △ABC为等边三角形, ∠BDC=120°. 求证: AD=BD+CD.
03. 如图,在 中,AB=AC, 点D是 外的一点,且 求证:
04.如图, 在等边△ABC中, 点D为边BC上一点, 交AD的延长线于点 F.
(1) 求 的度数;
(2) 若 BE=10, AF=15, 求AE的长.
05.如图, 都是等边三角形.
(1) 求证:
(2) 设BE, DC交于M, 连AM, 求 的值.
06.(1) 探究: 如图1, △ABC和△ADE都是等边三角形, 点D在边BC上.
①求 的大小;
②直接写出线段CD,CE,AC之间的数量关系;
(2)应用: 如图2, 在四边形 ABCD 中, AB=BC, ∠ABC=60°, P 是四边形ABCD 内一点, 且 求证:
(3)拓展:如图.3,在平面直角坐标系中,点A的坐标为(-4,0) ,点B是y轴上一个动点,以AB为边在AB的下方作等边△ABC,求OC的最小值.
专题十五 直角三角形中30°角所对的直角边等于斜边的一半
核心考点一 直接运用定理
01.如图, Rt△ABC中, ∠ACB=90°, CD⊥AB, 若∠A=30°, BD=1, 则AD的长为 ·
02. 如图, 在△ABC中, AB=AC, ∠B=30°, AD⊥AB交BC于点D, AD=3, 则BC的长是 ( )
A. 8 B. 9
C. 10 D. 11
核心考点二 先构造图形,再运用定理
03. 如图, 点C在△ABD的边BD上,AC=AB,若AD=8, CD=3,∠D=60°, 则BC的长是 .
04.如图, 已知∠AOB=30°, P是∠AOB平分线上一点, CP∥OB, 交OA于点C, PD⊥OB, 垂足为点D, 且PC=4, 则PD的长是 ( )
A. 1 B. 2
C. 4 D. 8
05. 如图, 在Rt△ABC中, ∠C=90°, AB的垂直平分线DE交BC于点E, 若 则BE的长度是 .
06.如图, △ABC中, BC=2AC, ∠DBC=∠ACB=120°, BD=BC, CD交边AB于点E.
(1) 求∠ACE的度数;
(2) 求证: DE=3CE.
07. 已知 为等腰三角形,BC边上的高恰好等于BC边长的一半,则∠BAC的大小为 .
08.如图, 在. 中, ∠C=30°, 点D是AC的中点,. 交BC于E, 点O在DE上, OA=OB, OD=2, OE=4, 则BE的长为 .
09如图, 在 中, CM平分 交AB于点M,过点M作 BC交AC于点N, 且MN平分∠AMC, 若AN=1, 则BC的长为 .
C
10.如图, △ABC和 是一副直角三角板,其中 , 延长 AD,CB交于点E, 延长AB至F, 使BF=2AB, 那么∠F的度数是 .
核心考点三 构造全等,再结合定理解题
11.如图, 在 中, , 点D, E, F分别为边AC, AB, CB上的点,且 为等边三角形,若 则 的值为 .
B
