2024-2025学年人教版八年级数学上册第十一章 三角形 中档题专题提优(共16专题,无答案)
文档属性
| 名称 | 2024-2025学年人教版八年级数学上册第十一章 三角形 中档题专题提优(共16专题,无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-18 19:11:00 | ||
图片预览


文档简介
第十一章 三角形 中档题专题提优
专题一 三角形的边
核心考点一 两边之和大于第三边
01 以下各组线段中,能组成三角形的是 ( )
A. 2, 2, 4 B. 3, 2, 6 C. 1, 2, 2 D. 1, 2, 3
02.若三角形两边长分别是3,5,则第三边c的范围是 .
03. 在△ABC中, AB=2cm, AC=5cm, 若△ABC的周长为整数, △ABC的周长不可能是 ( )
A. 10cm B. 11cm C. 12cm D. 13cm
04. 若a, b, c表示△ABC的三边长, 则|a-b-c|+|b-c-a|+|c-b-a|= .
核心考点二 等腰三角形的三边关系
05. 已知等腰三角形的两边长分别为5和6,则这个等腰三角形的周长为( )
A. 11 B. 16 C. 17 D. 16或17
06.已知等腰三角形的周长为18,一边长为4,则它的底边长是 ( )
A. 4 B. 10 C. 4或7 D. 4或10
07. 一个等腰三角形的一边长为4cm,一边长为9cm,则它的周长是 .
08.在等腰△ABC中, AB=AC, 其周长为20cm,则AB边的取值范围是 ( )
A. 1cmC. 4cm核心考点三 同一个未知数表示已知大小关系的三边
09. 已知一个三角形的三边长分别是a+4,a+5和a+6,则a的取值范围是 .
10. 一个等腰三角形的周长为12cm,且底边、腰长相差3cm,求这个三角形的各边长.
核心考点四 动态三边关系求取值范围和最值
11.如图, AB=3, BC=5, 将线段AB绕着点 B旋转, 连接AC, 在旋转过程中, 线段AC的最大值是 ,最小值是 ,AC的取值范围是 .
核心考点五 同一个未知数表示未知大小关系的三边与分类讨论
12. 已知三角形的三边长为x, ,并且最长边与最短边x之差是8,则三角形的最短边的长为 .
13. 在周长为25的三角形中,最短边是x,另一边是2x-3,则x的取值范围( )
14.已知等腰△ABC中, AB=8, BC=x+2, AC=2x, 求 的周长.
15.已知a,b,c是△ABC的三边长, 若 且 的周长不超过20cm,求a的取值范围.
16.小刚准备用一段长44米的篱笆围成三角形,用于养鸡. 已知第一条边长为x米,第二条边长是第一条边长的3倍多6米.
(1) 若能围成一个等腰三角形,求三边长;
(2) 若第一条边长最短,写出x的取值范围 .
核心考点六 利用三角形三边关系证明线段的不等关系
17.如图, P为 角平分线AD 上一点,求证:
专题二 三角形的高、中线和角平分线
核心考点一 三角形的高
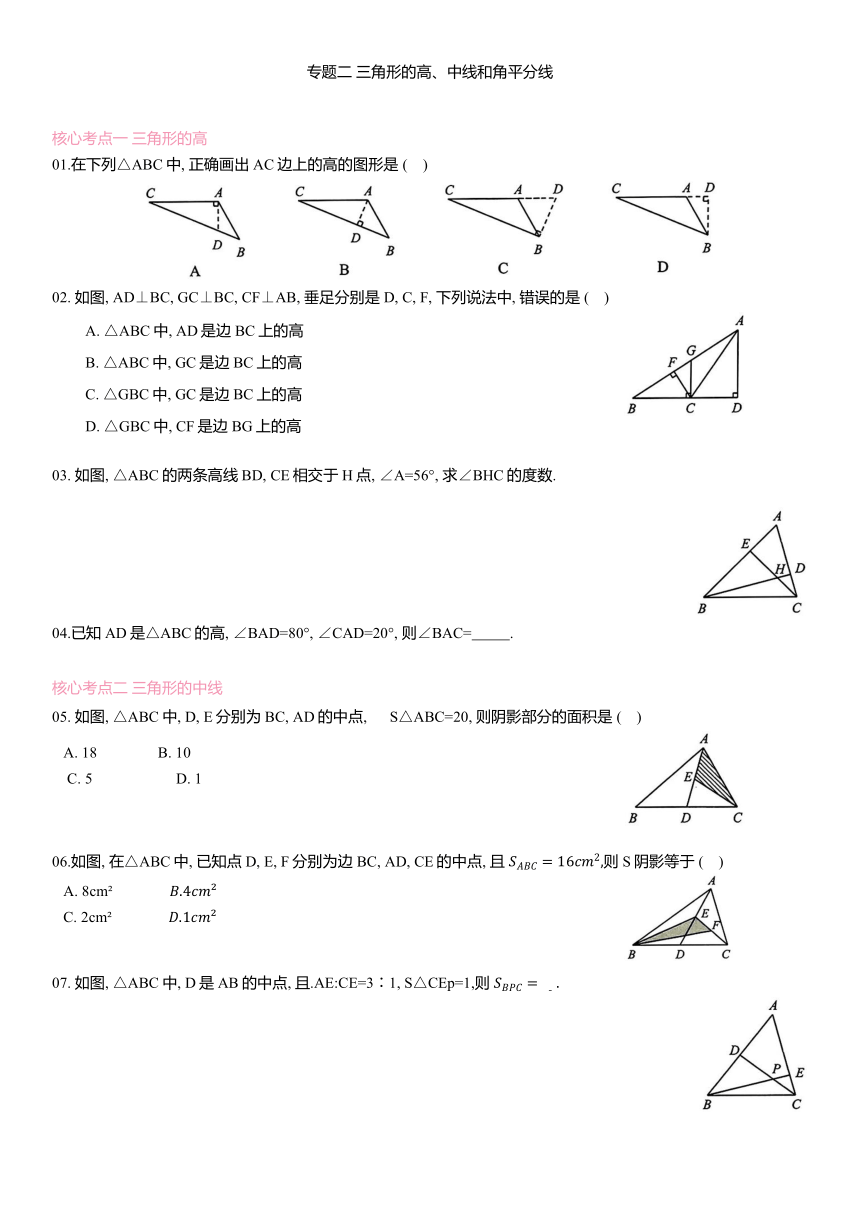
01.在下列△ABC中, 正确画出AC边上的高的图形是 ( )
02. 如图, AD⊥BC, GC⊥BC, CF⊥AB, 垂足分别是D, C, F, 下列说法中, 错误的是 ( )
A. △ABC中, AD是边BC上的高
B. △ABC中, GC是边BC上的高
C. △GBC中, GC是边BC上的高
D. △GBC中, CF是边 BG上的高
03. 如图, △ABC的两条高线BD, CE相交于H点, ∠A=56°, 求∠BHC的度数.
04.已知AD是△ABC的高, ∠BAD=80°, ∠CAD=20°, 则∠BAC= .
核心考点二 三角形的中线
05. 如图, △ABC中, D, E分别为BC, AD的中点, S△ABC=20, 则阴影部分的面积是 ( )
A. 18 B. 10
C. 5 D. 1
06.如图, 在△ABC中, 已知点D, E, F分别为边 BC, AD, CE的中点, 且 则S阴影等于 ( )
A. 8cm
C. 2cm
07. 如图, △ABC中, D是AB的中点, 且.AE:CE=3∶1, S△CEp=1,则
08三角形的三条中线的交点叫三角形的 .
核心考点三 三角形的角平分线
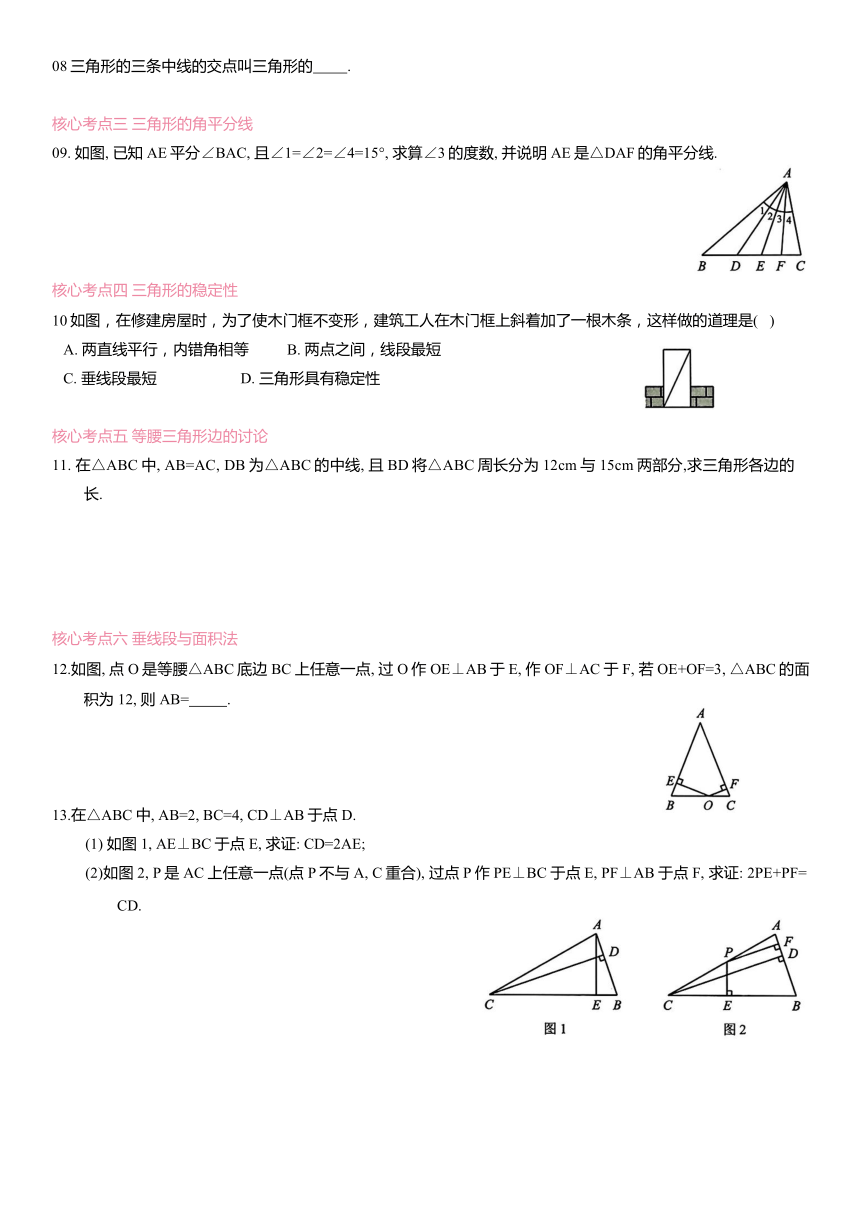
09. 如图, 已知AE平分∠BAC, 且∠1=∠2=∠4=15°, 求算∠3的度数, 并说明AE是△DAF的角平分线.
核心考点四 三角形的稳定性
10如图,在修建房屋时,为了使木门框不变形,建筑工人在木门框上斜着加了一根木条,这样做的道理是( )
A. 两直线平行,内错角相等 B. 两点之间,线段最短
C. 垂线段最短 D. 三角形具有稳定性
核心考点五 等腰三角形边的讨论
11. 在△ABC中, AB=AC, DB为△ABC的中线, 且BD将△ABC周长分为12cm与15cm两部分,求三角形各边的长.
核心考点六 垂线段与面积法
12.如图, 点O是等腰△ABC底边BC上任意一点, 过O作OE⊥AB于E, 作OF⊥AC于 F, 若OE+OF=3, △ABC的面积为12, 则AB= .
13.在△ABC中, AB=2, BC=4, CD⊥AB于点D.
(1) 如图1, AE⊥BC于点 E, 求证: CD=2AE;
(2)如图2, P是AC上任意一点(点P不与A, C重合), 过点P作PE⊥BC于点E, PF⊥AB于点 F, 求证: 2PE+PF=CD.
专题三 三角形的内外角
核心考点一 三角形的内角
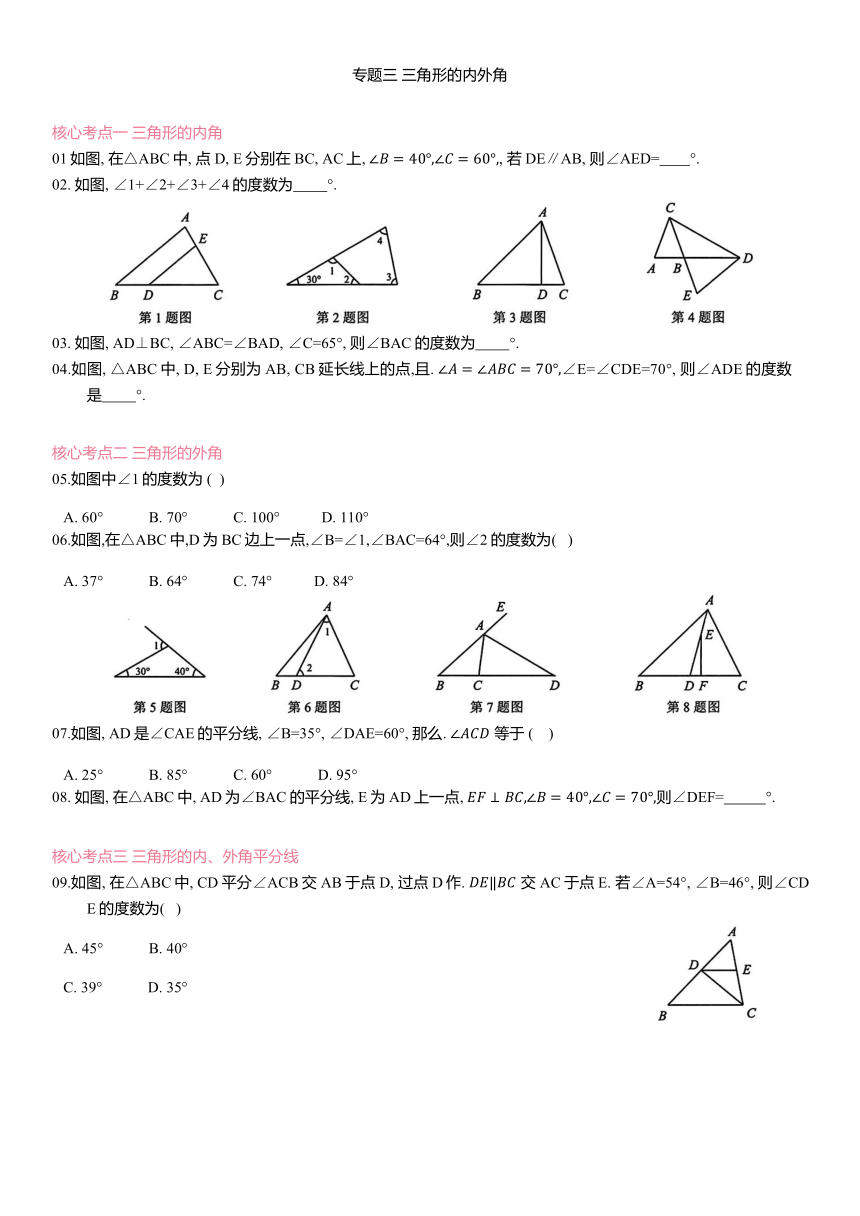
01如图, 在△ABC中, 点D, E分别在BC, AC上, , 若DE∥AB, 则∠AED= °.
02. 如图, ∠1+∠2+∠3+∠4的度数为 °.
03. 如图, AD⊥BC, ∠ABC=∠BAD, ∠C=65°, 则∠BAC的度数为 °.
04.如图, △ABC中, D, E分别为AB, CB延长线上的点,且. ∠E=∠CDE=70°, 则∠ADE的度数是 °.
核心考点二 三角形的外角
05.如图中∠1的度数为 ( )
A. 60° B. 70° C. 100° D. 110°
06.如图,在△ABC中,D为BC边上一点,∠B=∠1,∠BAC=64°,则∠2的度数为( )
A. 37° B. 64° C. 74° D. 84°
07.如图, AD是∠CAE的平分线, ∠B=35°, ∠DAE=60°, 那么. 等于 ( )
A. 25° B. 85° C. 60° D. 95°
08. 如图, 在△ABC中, AD为∠BAC的平分线, E为AD上一点, 则∠DEF= °.
核心考点三 三角形的内、外角平分线
09.如图, 在△ABC中, CD平分∠ACB交AB于点D, 过点D作. 交AC于点E. 若∠A=54°, ∠B=46°, 则∠CDE的度数为( )
A. 45° B. 40°
C. 39° D. 35°
10. 如图, △ABC中, ∠ACB和∠CAB的平分线交于点O, 且∠O=110°, 则∠B的度数为 ( )
A. 45° B. 50°
C. 40° D. 55°
B
11.如图, BE, CF是△ABC的角平分线, ∠ABC=80°,∠ACB=60°, EB, CF相交于D,则∠CDE的度数是 ( )
A. 130° B. 70°
C. 80° D. 75°
核心考点四 设参导角
12.如图,在△ABC中,∠ABC=∠ACB,点P为△ABC内一点,且∠PBC=∠PCA,∠A=α,求∠BPC的度数.
13.△ABC中, BD平分∠ABC, CE平分∠ACB, BD与CE交于点M.
(1) 如图1, 若∠ABC=70°, ∠ACB=50°, 求∠BMC的度数;
(2) 如图2, 若MN⊥BC于N, ∠A=60°, 求图中∠1-∠2的值;
(3) 若∠BEC=x, ∠BDC=y, 那么∠BMC= .
专题四 直角三角形的性质与判定
核心考点一 直角三角形的两锐角互余
01. 如图, Rt△ABC, ∠ACB=90°, CD⊥AB 于D, ∠BCD=40°, 则∠A的度数为( )
A. 40° B. 38°
C. 50° D. 30°
02. 如图, 在Rt△ADB中, ∠D=90°, C为AD上一点, ∠ACB=6x, 则x可能是 ( )
A. 10° B. 20°
C. 30° D. 40°
03.如图是由一副三角板拼凑得到的,图中的∠ABC的度数为( )
A. 50° B. 60°
C. 75° D. 80°
04.如图, 在锐角△ABC中, CD, BE分别是AB, AC边上的高, CD, BE交于点P,∠A=50°, 则∠BPC的度数是 ( )
A. 150° B. 130°
C. 120° D. 100°
05. 如图, 在△ABC中, ∠ABC=∠C=2∠A, BD⊥AC于D, 求 的度数.
核心考点二 从角的角度判定直角三角形
06.满足下列条件的△ABC中, 不是直角三角形的是 ( )
A. ∠A-∠B=∠C B. ∠A∶∠B∶∠C=3∶4∶7
C. ∠A=2∠B=3∠C D. ∠A=9°, ∠B=81°
07.在下列条件中: ①∠A+∠B=∠C; ②∠A∶∠B∶∠C=3∶7∶4; ③∠A=90°-∠B; 中,能确定△ABC是直角三角形的条件有 ( )
A. ①③ B. ①④ C. ①②③ D. ①②③④
核心考点三 直角三角形与角平分线
08.如图, △ABC中, ∠C=90°, AD平分 于F, 交AD于点P. 求证:∠CPD=∠CDP.
09. 如图, Rt△ACB中, ∠ACB=90°, CD⊥AB于 D, BE平分 交AC于E, 交CD于点F, 若∠A-∠EBA=12°, 则∠CFB的度数为 °.
10.如图, 在△ABC中, ∠B=25°, ∠BAC=31°, 过点A作BC边上的高, 交 BC的延长线于点 D, CE平分∠ACD, 交AD于点E.
求: (1)∠ACD的度数; (2) ∠AEC的度数.
11.如图1, 在 中, AD平分
(1) 求 的度数;
(2) 如图2, 若把“AE⊥BC”变成“点F在DA的延长线上, 其它条件不变,求 的度数.
专题五 多边形的边、角和对角线
核心考点一 多边形的内角与边数的关系
01.一个正多边形的每一个内角均为120°,它是一个 ( )
A. 正方形 B. 正三角形 C. 正八边形 D. 正六边形
02.已知正多边形的一个内角为144°,则该正多边形的边数为( )
A. 12 B. 10 C. 8 D. 6
03.一个多边形内角和是1080°, 则这个多边形是 ( )
A. 六边形 B. 七边形 C. 八边形 D. 九边形
04.如果剪掉四边形的一个角,那么所得多边形的内角和的度数不可能是 ( )
A. 180° B. 360° C. 540° D. 720°
05.如图, 在由线段AB, CD, DF, BF, CA组成的平面图形中,∠D=28°, 则∠A+∠B+∠C+∠F的度数为 ( )
A. 62° B. 152°
C. 208° D. 236°
核心考点二 多边形的外角
06.已知一个多边形的每个外角都是36°,则这个多边形的内角和是 ( )
A. 1260° B. 1440° C. 1620° D. 1800°
07.一个多边形的内角和与它的外角和相等,则它是 ( )
A. 三角形 B. 四边形 C. 五边形 D. 六边形
08.如果一个多边形的内角和是外角和的3倍,则这个多边形的边数是 ( )
A. 6 B. 7 C. 8 D. 9
09.如图, 小明从O点出发, 前进6米后向右转20°, 再前进6米后又向右转20°, …,这样一直走下去,他第一次回到出发点O时一共走了 ( )
A. 144米 B. 120米
C. 108米 D. 72米
10如图, 七边形 ABCDEFG 中, EF, BA的延长线相交于点P, 若∠ABC, ∠BCD,∠CDE, ∠DEF的外角的度数和为230°, 则∠P的度数为( )
A. 40° B. 45°
C. 50° D. 55°
核心考点三 多边形的对角线
11.已知一个多边形的内角和为1620°,则多边形的总对角线条数为( )
A. 27 B. 44 C. 35 D. 54
12. 多边形每一个内角都等于150°,则从此多边形一个顶点发出的对角线有 ( )
A. 7条 B. 8条 C. 9条 D. 10条
13.从n边形的一个顶点出发,可以作5条对角线,则n的值是 ( )
A. 6 B. 8 C. 10 D. 12
14.从7边形的一个顶点作对角线,把这个7边形分成三角形的个数是 ( )
A. 7个 B. 6个 C. 5个 D. 4个
核心考点四 镶嵌
15.下列一种完全相同的正多边形能镶嵌成一个平面图案的是 ( )
A. 正六边形 B. 正八边形 C. 正七边形 D. 正五边形
16. 用形状、大小完全相同的下列图形,不能拼成既无缝隙又不重叠的图形的是( )
A. 三角形 B. 四边形 C. 正五边形 D. 正六边形
核心考点五 多边形的内外角及角平分线
17. 如图, 在五边形ABCDE中, ∠A+∠B+∠E=300°, DP, CP分别平分∠EDC, ∠BCD, 则∠P的 大小是 度.
18. 如图, 在正五边形ABCDE中, BG平分∠ABC, DG平分正五边形的外角∠EDF, 则∠G=( )
A. 36° B. 54°
C. 60° D. 72°
19. 如图, 在四边形ABCD中, ∠A+∠C=180°, BE平分∠ABC, DF平分∠CDA, BE∥DF.求证: DC⊥BC.
20. 已知在四边形ABCD中, 如图, (n>2) , 则∠BED的度数为 ( )
专题六 设参处理与方程思想求角度
01. 如图, △ABC中, ∠1=∠2, ∠ABC=∠C=∠3=α, 求α.
C
02.如图, 点D在BC上, ∠B=∠C=∠BAD, ∠CAD=∠CDA, 求∠B的度数.
03.如图, 在△ABC中, ∠B=∠C, 点D为BC边上一点, 点E在AC边上, ∠ADE=∠AED=70°, ∠CDE=15°, 则∠BAD= ( )
A. 55° B. 40°
C. 30° D. 20°
C
04. 如图, △ABC中, ∠BAC=∠ACB, M, N为BC上两点, 且. 求∠MAC的度数.
05. 如图, ∠CDM, ∠FCA为△ACD的两个外角, 射线DE, CG分别平分 CG交DA 的延长线于点G, ∠E=∠1, ∠G=∠2, 求 的度数.
专题七 导角模型 ( 1)——双内角平分线
核心考点一 认识模型
01. 如图,点P是△ABC两条内角平分线的交点,求证:
核心考点二 应用模型
02.如图, 在△ABC中,∠C=80°, ∠CAB, ∠CBA的平分线相交于点D, BD的延长线交AC于点E, 求∠ADE的度数.
03.已知在 中,
(1) 如图1, 的平分线交于点O,求 的度数;
(2)如图2, 的三等分线交于点( 则
04. (1) 如图1, 在 中, DP, CP分别平分. 和 ,直接写出 与 的数量关系为 ;
(2)如图2, 在四边形ABCD 中, DP, CP 分别平分. 和 试写出 与 的数量关系.
专题八 导角模型(2) ——双外角平分线
核心考点一 认识模型
01. 如图,点P是△ABC两条外角平分线的交点,求证:
核心考点二 应用模型
02. 如图,在平面直角坐标系中,点A为x轴上的一点,点B为y轴上的一点,AC平分∠BAx,BC平分∠ABy, 求∠C的度数.
03. 如图, △ABC的外角∠ACE和外角∠CAF的平分线交于点P, 已知 则∠B的度数 为 ( )
A. 42° B. 40°
C. 38° D. 35°
04. 在△ABC中, ∠ABC, ∠ACB的平分线交于点O, 的外角平分线交于点D.
(1) 请探究∠BOC的度数与∠BDC的度数有什么数量关系 并证明你的结论;
(2) 若△ABC的三个外角平分线的交点为D, E, F, 请判断 是锐角三角形还是钝角三角形或直角三角形 并证明你的结论.
专题九 导角模型(3)——内外角平分线
核心考点一 认识模型
01. 如图, 点D是BC延长线上一点, PB平分∠ABC, PC平分∠ACD. 求证:
核心考点二 应用模型
02. 如图,在平面直角坐标系中,点A为x轴上的一点,点B为y轴上的一点,AD平分∠BAx,BP平分∠OBA, BP与DA的延长线交于点P, 求∠P的度数.
03如图, 等腰△ABC中, 顶角∠A=42°, 点E, F是内角 与外角∠ACD三等分线的交点, 则∠BFC= °.
04. 已知D, E分别为△ABC中AB, BC上的动点, 直线DE与直线AC相交于 F, 的平分线与 的平分线相交于 P,∠ACB的平分线与. 的平分线相交于 Q.
(1) 如图1, 当F在AC的延长线上时, 求∠P与. 之间的数量关系;
(2) 如图2, 当F在AC的反向延长线上时, 求∠P与. 之间的数量关系(用等式表示) .
专题十 导角模型(4)——角平分线与垂线
核心考点一 认识模型
01. 如图, △ABC中, AD平分∠BAC, AE⊥BC, 求证:
核心考点二 应用模型
02. 如图, △ABC中, AD是高, AE平分∠BAC, ∠B=50°, ∠C=80°, 则.
核心考点三 模型变式
03.如图,△ABC中,AD平分∠BAC,P是BC延长线上一点,过P作 则∠EPD= °.
04.如图1, AE, AD分别是 的高和角平分线.
(1) 若. ,求∠DAE的度数;
(2)如图2,AD平分∠BAC,P是AD延长线上一点, 过P作 求证:
专题十一 导角模型(5) ——A 字模型
核心考点一 认识模型
01. 如图, ∠DAE的两边上各有一点B, C, 连接BC, 求证:
核心考点二 应用模型
02. 如图, ∠1+∠2的度数是( )
A. 90° B. 135°
C. 180° D. 270°
03. 如图, 在△ABC中, E, F分别是AB, AC上的点, ∠1+∠2=214°, 则∠A的度数为 ( )
A. 17° B. 34°
C. 68° D. 无法确定
04. 如图, △ABC中, ∠C=70°, 若沿图中虚线截去∠C, 则
A. 360° B. 250°
C. 180° D. 140°
05. 如图, 在△ABC中, ∠B=58°, 三角形两外角的平分线交于点E, 则.
核心考点三 构造模型
06. 如图, 已知∠C=30°, 则
专题十二 导角模型(6)——折叠模型
核心考点一 认识模型
01如图, 将∠BAC 沿 DE 向 内部折叠,A与 重合,若 则∠1+∠2= °.
02.如图,将一张三角形纸片ABC的一角折叠,使点A落在 外的点A'处,折痕为DE. 如果∠A=α, ∠CEA'=β, ∠BDA'=γ. 那么下列式子中正确的是 ( )
A. γ=α+β B. γ=α+2β
D. γ=2α+β
核心考点二 应用模型
03.如图,△ADC中, 点E和点F分别为AD, AC上的动点,把 纸片沿EF折叠,使得点A落在△ADC的外部A'处,若. 则 度数为 ( )
A. 20° B. 21°
C. 21.5° D. 22.5°
核心考点三 模型变式
04.把△ABC沿EF对折, 折叠后的图形如图所示. 若 则 的度数为 °.
专题十三 导角模型 (7) ——蝴蝶模型
核心考点一 认识模型
01. ① 如图1, ∠A+∠B ∠C+∠D; (填“>” “=”或“<”) 并简述其理由.
② 如图2, ∠A+∠B+∠C+∠D+∠E= .
③ 如图3, ∠A+∠B+∠C+∠D+∠E= .
④ 如图4, ∠F=50°, 则∠A+∠B+∠C+∠D+∠E= .
核心考点二 应用模型
02. 如图, 在△ABC中, D为BC延长线上的一点, DE⊥AB于E, 交AC于F,若∠A=40°, ∠D=45°,则∠ACD= .
核心考点三 构造模型
03.如图, 在△ABC中, ∠C=90°, AG⊥HG, BI∥GH, 求证: ∠CAG=∠CBI.
核心考点四 组合应用模型
04. 平面内, 四条线段AB, BC, CD, DA 首尾顺次相接, ∠ABC=24°, ∠ADC=42°.
(1) 如图1, ∠BAD和∠BCD的平分线交于点M, 求∠AMC的大小;
(2)如图2, 点E在BA的延长线上, ∠DAE的平分线和∠BCD 的平分线交于点N, 求∠ANC的大小.
专题十四 导角模型 (8) ——燕尾模型
核心考点一 认识模型
01. (1) 如图, 求证: ∠CDB=∠A+∠B+∠C.
(2)如图,∠ACD的平分线与∠ABD的平分线交于点E,试说明 和∠CDB 有何数量 关系
核心考点二 应用模型
02.形如燕尾的几何图形我们通常称之为“燕尾形”,如图是一个燕尾形,已知, 105°, ∠ABC=63°, ∠BAD=22°, 则∠BCD的度数为 °.
03. 如图, 已知在, 中, ,现将一块直角三角板放在 上,使三角板的两条直角边分别经过点B,C,直角顶点 D落在 的内部,则
A. 90° B. 60°
C. 50° D. 40°
04.如图, 若 则
核心考点三 构造模型
05.在社会实践手工课上,小茗同学设计了一个形状如图所示的零件,如果∠A=52°,∠B=25°, ∠C=30°, ∠D=35°, ∠E=72°, 那么∠F的度数是 ( )
A. 72° B. 70°
C. 65° D. 60°
06. 如图, 若∠AED=105°, ∠BFC=115°, 则∠A+∠B+∠C+∠D= .
核心考点四 模型拓展
07. 已知∠ABC与∠ADC的平分线交于点E.
(1) 如图,试探究∠E,∠A与∠C之间的数量关系,并说明理由;
(2)如图, 若∠ABD, ∠BAC的平分线交于点E, 则∠C, ∠D与∠E之间有怎样的数量关系
08. 如图, ∠ABD, ∠ACD的角平分线交于点P, 若∠A=50°, ∠D=10°, 则∠P 的度数为 .
专题十五 实践与操作——图形的拼接
01.如图, 将锐角△ABC沿DH, GF, FE翻折, 三个顶点均落在点O处. 若 则∠2的度数为( )
A. 75° B. 85°
C. 90° D. 95°
02.把一幅含45°、30°的三角板如图摆放, 其中 则∠α+∠β= ( )
A. 180° B. 200°
C. 210° D. 240°
03. 如图,两本长方形的书按如图所示方式叠放在一起,则∠3+∠2+2∠1=( )
A. 360° B. 540°
C. 720° D. 以上答案均不对
04. 如图,由内角分别相等的四边形、五边形、六边形组合而成的图形中, 则 2的度数为 度.
05如图, 以正六边形ADHGFE的一边AD为边向外作正方形ABCD, 求 的度数.
专题十六 综合与运用——设参导角的处理策略
01. 如图, 在△ABC中, ∠ABC=67°, ∠ACB=34°, AD是△ABC的角平分线, 过D点作DE∥AB 交AC于点E, 则∠ADE的度数为 ( )
A. 40° B. 39.5°
C. 79° D. 44.5°
02. 如图, △ABC中, 三条内角平分线AD, BF, CE相交于点O, OG⊥BC. 求证: ∠BOD=∠GOC.
03.(1) 如图1, 四边形ABCD中, ∠ABC和∠BCD的平分线交于点P, 已知∠A+∠D=140°, 求∠P的度数;
(2)如图2,四边形ABCD中, ∠ABC和∠ADC外角的三等分线交于点P, 已知∠ABC=3∠ABP,∠ADE=3∠ADP, 请写出∠A, ∠C与∠P的数量关系, 并证明;
(3)如图3,E在CD边的延长线上,F在AD边的延长线上,∠BAD和∠DEF的平分线交于点P,请直接写出∠B, ∠C, ∠F, ∠P的数量关系: .
专题一 三角形的边
核心考点一 两边之和大于第三边
01 以下各组线段中,能组成三角形的是 ( )
A. 2, 2, 4 B. 3, 2, 6 C. 1, 2, 2 D. 1, 2, 3
02.若三角形两边长分别是3,5,则第三边c的范围是 .
03. 在△ABC中, AB=2cm, AC=5cm, 若△ABC的周长为整数, △ABC的周长不可能是 ( )
A. 10cm B. 11cm C. 12cm D. 13cm
04. 若a, b, c表示△ABC的三边长, 则|a-b-c|+|b-c-a|+|c-b-a|= .
核心考点二 等腰三角形的三边关系
05. 已知等腰三角形的两边长分别为5和6,则这个等腰三角形的周长为( )
A. 11 B. 16 C. 17 D. 16或17
06.已知等腰三角形的周长为18,一边长为4,则它的底边长是 ( )
A. 4 B. 10 C. 4或7 D. 4或10
07. 一个等腰三角形的一边长为4cm,一边长为9cm,则它的周长是 .
08.在等腰△ABC中, AB=AC, 其周长为20cm,则AB边的取值范围是 ( )
A. 1cm
09. 已知一个三角形的三边长分别是a+4,a+5和a+6,则a的取值范围是 .
10. 一个等腰三角形的周长为12cm,且底边、腰长相差3cm,求这个三角形的各边长.
核心考点四 动态三边关系求取值范围和最值
11.如图, AB=3, BC=5, 将线段AB绕着点 B旋转, 连接AC, 在旋转过程中, 线段AC的最大值是 ,最小值是 ,AC的取值范围是 .
核心考点五 同一个未知数表示未知大小关系的三边与分类讨论
12. 已知三角形的三边长为x, ,并且最长边与最短边x之差是8,则三角形的最短边的长为 .
13. 在周长为25的三角形中,最短边是x,另一边是2x-3,则x的取值范围( )
14.已知等腰△ABC中, AB=8, BC=x+2, AC=2x, 求 的周长.
15.已知a,b,c是△ABC的三边长, 若 且 的周长不超过20cm,求a的取值范围.
16.小刚准备用一段长44米的篱笆围成三角形,用于养鸡. 已知第一条边长为x米,第二条边长是第一条边长的3倍多6米.
(1) 若能围成一个等腰三角形,求三边长;
(2) 若第一条边长最短,写出x的取值范围 .
核心考点六 利用三角形三边关系证明线段的不等关系
17.如图, P为 角平分线AD 上一点,求证:
专题二 三角形的高、中线和角平分线
核心考点一 三角形的高
01.在下列△ABC中, 正确画出AC边上的高的图形是 ( )
02. 如图, AD⊥BC, GC⊥BC, CF⊥AB, 垂足分别是D, C, F, 下列说法中, 错误的是 ( )
A. △ABC中, AD是边BC上的高
B. △ABC中, GC是边BC上的高
C. △GBC中, GC是边BC上的高
D. △GBC中, CF是边 BG上的高
03. 如图, △ABC的两条高线BD, CE相交于H点, ∠A=56°, 求∠BHC的度数.
04.已知AD是△ABC的高, ∠BAD=80°, ∠CAD=20°, 则∠BAC= .
核心考点二 三角形的中线
05. 如图, △ABC中, D, E分别为BC, AD的中点, S△ABC=20, 则阴影部分的面积是 ( )
A. 18 B. 10
C. 5 D. 1
06.如图, 在△ABC中, 已知点D, E, F分别为边 BC, AD, CE的中点, 且 则S阴影等于 ( )
A. 8cm
C. 2cm
07. 如图, △ABC中, D是AB的中点, 且.AE:CE=3∶1, S△CEp=1,则
08三角形的三条中线的交点叫三角形的 .
核心考点三 三角形的角平分线
09. 如图, 已知AE平分∠BAC, 且∠1=∠2=∠4=15°, 求算∠3的度数, 并说明AE是△DAF的角平分线.
核心考点四 三角形的稳定性
10如图,在修建房屋时,为了使木门框不变形,建筑工人在木门框上斜着加了一根木条,这样做的道理是( )
A. 两直线平行,内错角相等 B. 两点之间,线段最短
C. 垂线段最短 D. 三角形具有稳定性
核心考点五 等腰三角形边的讨论
11. 在△ABC中, AB=AC, DB为△ABC的中线, 且BD将△ABC周长分为12cm与15cm两部分,求三角形各边的长.
核心考点六 垂线段与面积法
12.如图, 点O是等腰△ABC底边BC上任意一点, 过O作OE⊥AB于E, 作OF⊥AC于 F, 若OE+OF=3, △ABC的面积为12, 则AB= .
13.在△ABC中, AB=2, BC=4, CD⊥AB于点D.
(1) 如图1, AE⊥BC于点 E, 求证: CD=2AE;
(2)如图2, P是AC上任意一点(点P不与A, C重合), 过点P作PE⊥BC于点E, PF⊥AB于点 F, 求证: 2PE+PF=CD.
专题三 三角形的内外角
核心考点一 三角形的内角
01如图, 在△ABC中, 点D, E分别在BC, AC上, , 若DE∥AB, 则∠AED= °.
02. 如图, ∠1+∠2+∠3+∠4的度数为 °.
03. 如图, AD⊥BC, ∠ABC=∠BAD, ∠C=65°, 则∠BAC的度数为 °.
04.如图, △ABC中, D, E分别为AB, CB延长线上的点,且. ∠E=∠CDE=70°, 则∠ADE的度数是 °.
核心考点二 三角形的外角
05.如图中∠1的度数为 ( )
A. 60° B. 70° C. 100° D. 110°
06.如图,在△ABC中,D为BC边上一点,∠B=∠1,∠BAC=64°,则∠2的度数为( )
A. 37° B. 64° C. 74° D. 84°
07.如图, AD是∠CAE的平分线, ∠B=35°, ∠DAE=60°, 那么. 等于 ( )
A. 25° B. 85° C. 60° D. 95°
08. 如图, 在△ABC中, AD为∠BAC的平分线, E为AD上一点, 则∠DEF= °.
核心考点三 三角形的内、外角平分线
09.如图, 在△ABC中, CD平分∠ACB交AB于点D, 过点D作. 交AC于点E. 若∠A=54°, ∠B=46°, 则∠CDE的度数为( )
A. 45° B. 40°
C. 39° D. 35°
10. 如图, △ABC中, ∠ACB和∠CAB的平分线交于点O, 且∠O=110°, 则∠B的度数为 ( )
A. 45° B. 50°
C. 40° D. 55°
B
11.如图, BE, CF是△ABC的角平分线, ∠ABC=80°,∠ACB=60°, EB, CF相交于D,则∠CDE的度数是 ( )
A. 130° B. 70°
C. 80° D. 75°
核心考点四 设参导角
12.如图,在△ABC中,∠ABC=∠ACB,点P为△ABC内一点,且∠PBC=∠PCA,∠A=α,求∠BPC的度数.
13.△ABC中, BD平分∠ABC, CE平分∠ACB, BD与CE交于点M.
(1) 如图1, 若∠ABC=70°, ∠ACB=50°, 求∠BMC的度数;
(2) 如图2, 若MN⊥BC于N, ∠A=60°, 求图中∠1-∠2的值;
(3) 若∠BEC=x, ∠BDC=y, 那么∠BMC= .
专题四 直角三角形的性质与判定
核心考点一 直角三角形的两锐角互余
01. 如图, Rt△ABC, ∠ACB=90°, CD⊥AB 于D, ∠BCD=40°, 则∠A的度数为( )
A. 40° B. 38°
C. 50° D. 30°
02. 如图, 在Rt△ADB中, ∠D=90°, C为AD上一点, ∠ACB=6x, 则x可能是 ( )
A. 10° B. 20°
C. 30° D. 40°
03.如图是由一副三角板拼凑得到的,图中的∠ABC的度数为( )
A. 50° B. 60°
C. 75° D. 80°
04.如图, 在锐角△ABC中, CD, BE分别是AB, AC边上的高, CD, BE交于点P,∠A=50°, 则∠BPC的度数是 ( )
A. 150° B. 130°
C. 120° D. 100°
05. 如图, 在△ABC中, ∠ABC=∠C=2∠A, BD⊥AC于D, 求 的度数.
核心考点二 从角的角度判定直角三角形
06.满足下列条件的△ABC中, 不是直角三角形的是 ( )
A. ∠A-∠B=∠C B. ∠A∶∠B∶∠C=3∶4∶7
C. ∠A=2∠B=3∠C D. ∠A=9°, ∠B=81°
07.在下列条件中: ①∠A+∠B=∠C; ②∠A∶∠B∶∠C=3∶7∶4; ③∠A=90°-∠B; 中,能确定△ABC是直角三角形的条件有 ( )
A. ①③ B. ①④ C. ①②③ D. ①②③④
核心考点三 直角三角形与角平分线
08.如图, △ABC中, ∠C=90°, AD平分 于F, 交AD于点P. 求证:∠CPD=∠CDP.
09. 如图, Rt△ACB中, ∠ACB=90°, CD⊥AB于 D, BE平分 交AC于E, 交CD于点F, 若∠A-∠EBA=12°, 则∠CFB的度数为 °.
10.如图, 在△ABC中, ∠B=25°, ∠BAC=31°, 过点A作BC边上的高, 交 BC的延长线于点 D, CE平分∠ACD, 交AD于点E.
求: (1)∠ACD的度数; (2) ∠AEC的度数.
11.如图1, 在 中, AD平分
(1) 求 的度数;
(2) 如图2, 若把“AE⊥BC”变成“点F在DA的延长线上, 其它条件不变,求 的度数.
专题五 多边形的边、角和对角线
核心考点一 多边形的内角与边数的关系
01.一个正多边形的每一个内角均为120°,它是一个 ( )
A. 正方形 B. 正三角形 C. 正八边形 D. 正六边形
02.已知正多边形的一个内角为144°,则该正多边形的边数为( )
A. 12 B. 10 C. 8 D. 6
03.一个多边形内角和是1080°, 则这个多边形是 ( )
A. 六边形 B. 七边形 C. 八边形 D. 九边形
04.如果剪掉四边形的一个角,那么所得多边形的内角和的度数不可能是 ( )
A. 180° B. 360° C. 540° D. 720°
05.如图, 在由线段AB, CD, DF, BF, CA组成的平面图形中,∠D=28°, 则∠A+∠B+∠C+∠F的度数为 ( )
A. 62° B. 152°
C. 208° D. 236°
核心考点二 多边形的外角
06.已知一个多边形的每个外角都是36°,则这个多边形的内角和是 ( )
A. 1260° B. 1440° C. 1620° D. 1800°
07.一个多边形的内角和与它的外角和相等,则它是 ( )
A. 三角形 B. 四边形 C. 五边形 D. 六边形
08.如果一个多边形的内角和是外角和的3倍,则这个多边形的边数是 ( )
A. 6 B. 7 C. 8 D. 9
09.如图, 小明从O点出发, 前进6米后向右转20°, 再前进6米后又向右转20°, …,这样一直走下去,他第一次回到出发点O时一共走了 ( )
A. 144米 B. 120米
C. 108米 D. 72米
10如图, 七边形 ABCDEFG 中, EF, BA的延长线相交于点P, 若∠ABC, ∠BCD,∠CDE, ∠DEF的外角的度数和为230°, 则∠P的度数为( )
A. 40° B. 45°
C. 50° D. 55°
核心考点三 多边形的对角线
11.已知一个多边形的内角和为1620°,则多边形的总对角线条数为( )
A. 27 B. 44 C. 35 D. 54
12. 多边形每一个内角都等于150°,则从此多边形一个顶点发出的对角线有 ( )
A. 7条 B. 8条 C. 9条 D. 10条
13.从n边形的一个顶点出发,可以作5条对角线,则n的值是 ( )
A. 6 B. 8 C. 10 D. 12
14.从7边形的一个顶点作对角线,把这个7边形分成三角形的个数是 ( )
A. 7个 B. 6个 C. 5个 D. 4个
核心考点四 镶嵌
15.下列一种完全相同的正多边形能镶嵌成一个平面图案的是 ( )
A. 正六边形 B. 正八边形 C. 正七边形 D. 正五边形
16. 用形状、大小完全相同的下列图形,不能拼成既无缝隙又不重叠的图形的是( )
A. 三角形 B. 四边形 C. 正五边形 D. 正六边形
核心考点五 多边形的内外角及角平分线
17. 如图, 在五边形ABCDE中, ∠A+∠B+∠E=300°, DP, CP分别平分∠EDC, ∠BCD, 则∠P的 大小是 度.
18. 如图, 在正五边形ABCDE中, BG平分∠ABC, DG平分正五边形的外角∠EDF, 则∠G=( )
A. 36° B. 54°
C. 60° D. 72°
19. 如图, 在四边形ABCD中, ∠A+∠C=180°, BE平分∠ABC, DF平分∠CDA, BE∥DF.求证: DC⊥BC.
20. 已知在四边形ABCD中, 如图, (n>2) , 则∠BED的度数为 ( )
专题六 设参处理与方程思想求角度
01. 如图, △ABC中, ∠1=∠2, ∠ABC=∠C=∠3=α, 求α.
C
02.如图, 点D在BC上, ∠B=∠C=∠BAD, ∠CAD=∠CDA, 求∠B的度数.
03.如图, 在△ABC中, ∠B=∠C, 点D为BC边上一点, 点E在AC边上, ∠ADE=∠AED=70°, ∠CDE=15°, 则∠BAD= ( )
A. 55° B. 40°
C. 30° D. 20°
C
04. 如图, △ABC中, ∠BAC=∠ACB, M, N为BC上两点, 且. 求∠MAC的度数.
05. 如图, ∠CDM, ∠FCA为△ACD的两个外角, 射线DE, CG分别平分 CG交DA 的延长线于点G, ∠E=∠1, ∠G=∠2, 求 的度数.
专题七 导角模型 ( 1)——双内角平分线
核心考点一 认识模型
01. 如图,点P是△ABC两条内角平分线的交点,求证:
核心考点二 应用模型
02.如图, 在△ABC中,∠C=80°, ∠CAB, ∠CBA的平分线相交于点D, BD的延长线交AC于点E, 求∠ADE的度数.
03.已知在 中,
(1) 如图1, 的平分线交于点O,求 的度数;
(2)如图2, 的三等分线交于点( 则
04. (1) 如图1, 在 中, DP, CP分别平分. 和 ,直接写出 与 的数量关系为 ;
(2)如图2, 在四边形ABCD 中, DP, CP 分别平分. 和 试写出 与 的数量关系.
专题八 导角模型(2) ——双外角平分线
核心考点一 认识模型
01. 如图,点P是△ABC两条外角平分线的交点,求证:
核心考点二 应用模型
02. 如图,在平面直角坐标系中,点A为x轴上的一点,点B为y轴上的一点,AC平分∠BAx,BC平分∠ABy, 求∠C的度数.
03. 如图, △ABC的外角∠ACE和外角∠CAF的平分线交于点P, 已知 则∠B的度数 为 ( )
A. 42° B. 40°
C. 38° D. 35°
04. 在△ABC中, ∠ABC, ∠ACB的平分线交于点O, 的外角平分线交于点D.
(1) 请探究∠BOC的度数与∠BDC的度数有什么数量关系 并证明你的结论;
(2) 若△ABC的三个外角平分线的交点为D, E, F, 请判断 是锐角三角形还是钝角三角形或直角三角形 并证明你的结论.
专题九 导角模型(3)——内外角平分线
核心考点一 认识模型
01. 如图, 点D是BC延长线上一点, PB平分∠ABC, PC平分∠ACD. 求证:
核心考点二 应用模型
02. 如图,在平面直角坐标系中,点A为x轴上的一点,点B为y轴上的一点,AD平分∠BAx,BP平分∠OBA, BP与DA的延长线交于点P, 求∠P的度数.
03如图, 等腰△ABC中, 顶角∠A=42°, 点E, F是内角 与外角∠ACD三等分线的交点, 则∠BFC= °.
04. 已知D, E分别为△ABC中AB, BC上的动点, 直线DE与直线AC相交于 F, 的平分线与 的平分线相交于 P,∠ACB的平分线与. 的平分线相交于 Q.
(1) 如图1, 当F在AC的延长线上时, 求∠P与. 之间的数量关系;
(2) 如图2, 当F在AC的反向延长线上时, 求∠P与. 之间的数量关系(用等式表示) .
专题十 导角模型(4)——角平分线与垂线
核心考点一 认识模型
01. 如图, △ABC中, AD平分∠BAC, AE⊥BC, 求证:
核心考点二 应用模型
02. 如图, △ABC中, AD是高, AE平分∠BAC, ∠B=50°, ∠C=80°, 则.
核心考点三 模型变式
03.如图,△ABC中,AD平分∠BAC,P是BC延长线上一点,过P作 则∠EPD= °.
04.如图1, AE, AD分别是 的高和角平分线.
(1) 若. ,求∠DAE的度数;
(2)如图2,AD平分∠BAC,P是AD延长线上一点, 过P作 求证:
专题十一 导角模型(5) ——A 字模型
核心考点一 认识模型
01. 如图, ∠DAE的两边上各有一点B, C, 连接BC, 求证:
核心考点二 应用模型
02. 如图, ∠1+∠2的度数是( )
A. 90° B. 135°
C. 180° D. 270°
03. 如图, 在△ABC中, E, F分别是AB, AC上的点, ∠1+∠2=214°, 则∠A的度数为 ( )
A. 17° B. 34°
C. 68° D. 无法确定
04. 如图, △ABC中, ∠C=70°, 若沿图中虚线截去∠C, 则
A. 360° B. 250°
C. 180° D. 140°
05. 如图, 在△ABC中, ∠B=58°, 三角形两外角的平分线交于点E, 则.
核心考点三 构造模型
06. 如图, 已知∠C=30°, 则
专题十二 导角模型(6)——折叠模型
核心考点一 认识模型
01如图, 将∠BAC 沿 DE 向 内部折叠,A与 重合,若 则∠1+∠2= °.
02.如图,将一张三角形纸片ABC的一角折叠,使点A落在 外的点A'处,折痕为DE. 如果∠A=α, ∠CEA'=β, ∠BDA'=γ. 那么下列式子中正确的是 ( )
A. γ=α+β B. γ=α+2β
D. γ=2α+β
核心考点二 应用模型
03.如图,△ADC中, 点E和点F分别为AD, AC上的动点,把 纸片沿EF折叠,使得点A落在△ADC的外部A'处,若. 则 度数为 ( )
A. 20° B. 21°
C. 21.5° D. 22.5°
核心考点三 模型变式
04.把△ABC沿EF对折, 折叠后的图形如图所示. 若 则 的度数为 °.
专题十三 导角模型 (7) ——蝴蝶模型
核心考点一 认识模型
01. ① 如图1, ∠A+∠B ∠C+∠D; (填“>” “=”或“<”) 并简述其理由.
② 如图2, ∠A+∠B+∠C+∠D+∠E= .
③ 如图3, ∠A+∠B+∠C+∠D+∠E= .
④ 如图4, ∠F=50°, 则∠A+∠B+∠C+∠D+∠E= .
核心考点二 应用模型
02. 如图, 在△ABC中, D为BC延长线上的一点, DE⊥AB于E, 交AC于F,若∠A=40°, ∠D=45°,则∠ACD= .
核心考点三 构造模型
03.如图, 在△ABC中, ∠C=90°, AG⊥HG, BI∥GH, 求证: ∠CAG=∠CBI.
核心考点四 组合应用模型
04. 平面内, 四条线段AB, BC, CD, DA 首尾顺次相接, ∠ABC=24°, ∠ADC=42°.
(1) 如图1, ∠BAD和∠BCD的平分线交于点M, 求∠AMC的大小;
(2)如图2, 点E在BA的延长线上, ∠DAE的平分线和∠BCD 的平分线交于点N, 求∠ANC的大小.
专题十四 导角模型 (8) ——燕尾模型
核心考点一 认识模型
01. (1) 如图, 求证: ∠CDB=∠A+∠B+∠C.
(2)如图,∠ACD的平分线与∠ABD的平分线交于点E,试说明 和∠CDB 有何数量 关系
核心考点二 应用模型
02.形如燕尾的几何图形我们通常称之为“燕尾形”,如图是一个燕尾形,已知, 105°, ∠ABC=63°, ∠BAD=22°, 则∠BCD的度数为 °.
03. 如图, 已知在, 中, ,现将一块直角三角板放在 上,使三角板的两条直角边分别经过点B,C,直角顶点 D落在 的内部,则
A. 90° B. 60°
C. 50° D. 40°
04.如图, 若 则
核心考点三 构造模型
05.在社会实践手工课上,小茗同学设计了一个形状如图所示的零件,如果∠A=52°,∠B=25°, ∠C=30°, ∠D=35°, ∠E=72°, 那么∠F的度数是 ( )
A. 72° B. 70°
C. 65° D. 60°
06. 如图, 若∠AED=105°, ∠BFC=115°, 则∠A+∠B+∠C+∠D= .
核心考点四 模型拓展
07. 已知∠ABC与∠ADC的平分线交于点E.
(1) 如图,试探究∠E,∠A与∠C之间的数量关系,并说明理由;
(2)如图, 若∠ABD, ∠BAC的平分线交于点E, 则∠C, ∠D与∠E之间有怎样的数量关系
08. 如图, ∠ABD, ∠ACD的角平分线交于点P, 若∠A=50°, ∠D=10°, 则∠P 的度数为 .
专题十五 实践与操作——图形的拼接
01.如图, 将锐角△ABC沿DH, GF, FE翻折, 三个顶点均落在点O处. 若 则∠2的度数为( )
A. 75° B. 85°
C. 90° D. 95°
02.把一幅含45°、30°的三角板如图摆放, 其中 则∠α+∠β= ( )
A. 180° B. 200°
C. 210° D. 240°
03. 如图,两本长方形的书按如图所示方式叠放在一起,则∠3+∠2+2∠1=( )
A. 360° B. 540°
C. 720° D. 以上答案均不对
04. 如图,由内角分别相等的四边形、五边形、六边形组合而成的图形中, 则 2的度数为 度.
05如图, 以正六边形ADHGFE的一边AD为边向外作正方形ABCD, 求 的度数.
专题十六 综合与运用——设参导角的处理策略
01. 如图, 在△ABC中, ∠ABC=67°, ∠ACB=34°, AD是△ABC的角平分线, 过D点作DE∥AB 交AC于点E, 则∠ADE的度数为 ( )
A. 40° B. 39.5°
C. 79° D. 44.5°
02. 如图, △ABC中, 三条内角平分线AD, BF, CE相交于点O, OG⊥BC. 求证: ∠BOD=∠GOC.
03.(1) 如图1, 四边形ABCD中, ∠ABC和∠BCD的平分线交于点P, 已知∠A+∠D=140°, 求∠P的度数;
(2)如图2,四边形ABCD中, ∠ABC和∠ADC外角的三等分线交于点P, 已知∠ABC=3∠ABP,∠ADE=3∠ADP, 请写出∠A, ∠C与∠P的数量关系, 并证明;
(3)如图3,E在CD边的延长线上,F在AD边的延长线上,∠BAD和∠DEF的平分线交于点P,请直接写出∠B, ∠C, ∠F, ∠P的数量关系: .
