第一章空间向量与立体几何同步过关练习卷(含解析)-高二数学上学期人教A版(2019)选择性必修第一册
文档属性
| 名称 | 第一章空间向量与立体几何同步过关练习卷(含解析)-高二数学上学期人教A版(2019)选择性必修第一册 |  | |
| 格式 | docx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-19 14:46:07 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
第一章空间向量与立体几何同步过关练习卷-高二数学上学期人教A版(2019)选择性必修第一册
一、单选题
1.设,,,是半径为1的球的球面上的四个点.设,则不可能等于( )
A.3 B. C.4 D.
2.在三棱锥中,为的中点,则等于( )
A.-1 B.0 C.1 D.3
3.设向量,,不共面,已知,,,若A,C,D三点共线,则( )
A.1 B.2 C.3 D.4
4.下列说法正确的是( )
A.若向量、共线,则向量、所在的直线平行.
B.若、、是空间三个向量,则对空间任一向量,总存在唯一的有序实数组,使.
C.若向量、所在的直线是异面直线,则向量、一定不共线.
D.若三个向量、、两两共面,则三个向量、、一定共面.
5.已知四面体O-ABC,G1是△ABC的重心,G是OG1上一点,且OG=3GG1,若,则为( )
A. B.
C. D.
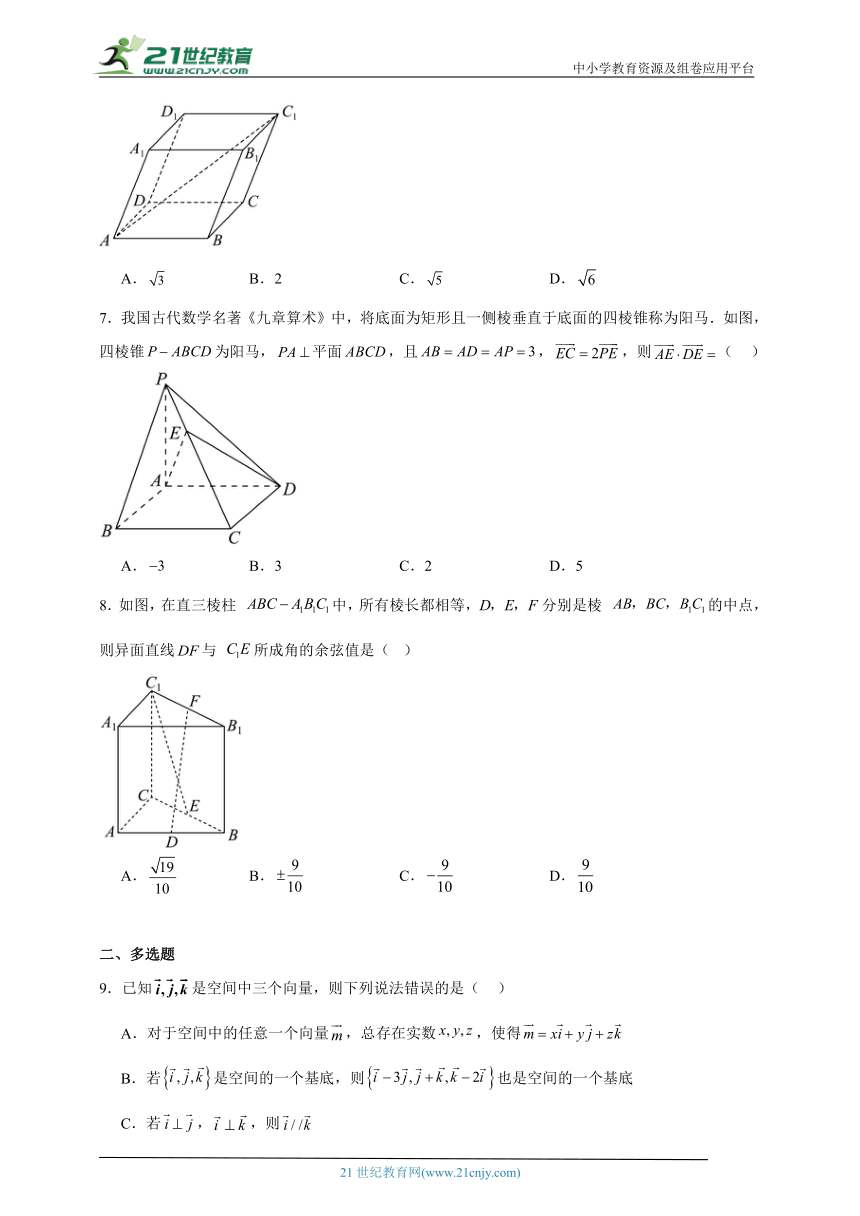
6.如图所示,在四棱柱中,底面为平行四边形,以顶点A为端点的三条棱长都为1,且两两夹角为,则的长为( )
A. B.2 C. D.
7.我国古代数学名著《九章算术》中,将底面为矩形且一侧棱垂直于底面的四棱锥称为阳马.如图,四棱锥为阳马,平面,且,,则( )
A. B.3 C.2 D.5
8.如图,在直三棱柱 中,所有棱长都相等,分别是棱 的中点,则异面直线与 所成角的余弦值是( )
A. B. C. D.
二、多选题
9.已知是空间中三个向量,则下列说法错误的是( )
A.对于空间中的任意一个向量,总存在实数,使得
B.若是空间的一个基底,则也是空间的一个基底
C.若,,则
D.若所在直线两两共面,则共面
10.已知点是平行四边形所在的平面外一点,如果,,,下列结论正确的有( )
A. B.与平面的夹角的余弦值为
C.是平面PBC的一个法向量 D.
11.如图,在平行六面体中,以顶点为端点的三条棱长都为1,且,则( )
A. B.
C.平面 D.直线与AC所成角的正弦值为
三、填空题
12.已知空间向量, 且,则 .
13.正四面体的棱长为2,设,,,则 .
14.已知平面的一个法向量,直线的方向向量,则直线与平面所成角的正弦值为 .
四、解答题
15.已知向量,向量,
(1)求向量,,的坐标;
(2)求与所成角的余弦值.
16.如图,四面体中,,分别为,上的点,且,,设,,.
(1)以为基底表示;
(2)若,且,,,求.
17.已知向量,,点,.
(1)求的值;
(2)在直线上存在一点E,使得,求点E的坐标.
18.如图,在三棱柱中,,,,平面底面,分别是的中点,P是与的交点.
(1)证明:平面平面;
(2)求平面与平面夹角的余弦值.
19.在如图所示的几何体中,四边形ABCD是正方形,四边形ADPQ是梯形,,,且.
(1)求证:平面PDC;
(2)求平面CPB与平面PBQ所成角的大小;
(3)已知点H在棱PD上,且异面直线AH与PB所成角的余弦值为,试确定点H的位置.
参考答案:
1.A
【分析】根据条件,得到,利用判断等号成立条件,确定不可能取的值.
【详解】因为,
且,所以,
而,当且仅当同向时,等号成立,
而A,,,在球面上,不可能共线,即不同向,
所以
且均小于直径长2,即,
综上,.
根据选项可知A不符合.
故选:A
2.C
【分析】由题意可得,再由数量积的运算律代入求解即可.
【详解】因为,
所以,
,
,
因为,
.
故选:C.
3.C
【分析】根据A,C,D三点共线,可得,则存在唯一实数,使得,再根据空间向量共线定理即可得解.
【详解】由,,
得,
因为A,C,D三点共线,所以,
则存在唯一实数,使得,
则,解得.
故选:C.
4.C
【分析】根据空间向量的相关概念以及空间向量基本定理分析判断.
【详解】对于A:若向量、共线,则向量、所在的直线平行或重合,故A错误;
对于B:根据空间向量基本定理可知,此时、、应是空间三个不共面的向量,故B错误;
对于C:反证:若向量、共线,则向量、所在的直线平行或重合,
这与向量、所在的直线是异面直线相矛盾,故C正确;
对于D:若三个向量、、两两共面,则三个向量、、不一定共面,
例如、、所在的直线为三棱锥的三条侧棱,故D错误;
故选:C.
5.A
【分析】连接AG1并延长,交BC于点E,利用向量加减、数乘几何意义用表示出,即可得答案.
【详解】如图所示,连接AG1并延长,交BC于点E,则点E为BC的中点,
,则,
由题设,,
所以.
故选:A
6.D
【分析】记,,,由,利用向量法即可求出的长.
【详解】解:记,,,
由题意可知,,
所以,
,
所以,即的长为,
故选:D.
7.B
【分析】根据题意建立空间直角坐标系计算求解即可.
【详解】因为平面,平面,
所以,
又因为四边形是矩形,所以,
以A为坐标原点,,,的方向分别为x,y,z轴的正方向建立如图所示的空间直角坐标系,
则,,则,
所以,,所以.
故选:B
8.D
【分析】利用平移法作出异面直线与 所成角,解三角形即可求得答案.
【详解】连接,因为在直三棱柱中,分别是棱的中点,
故,即四边形为平行四边形,所以,
则即为异面直线与 所成角或其补角;
直三棱柱中,所有棱长都相等,设其棱长为,连接,
则平面,故平面平面,
故,是棱的中点,故,
则,而
,又,故在中,,
由于异面直线所成角的范围,故异面直线与 所成角的余弦值是,
故选:D.
9.ACD
【分析】根据空间向量基本定理对选项一一判断即可得出答案.
【详解】对A,由空间向量基本定理,可知只有当不共面时,
才能作为基底,才能得到,故A错误;
对B,若是空间的一个基底,则不共面,
设,
则,因为无解,所以也不共面,
所以也是空间的一个基底,故B正确;
对C,若,,则不一定平行,故C错误;
对D,若所在直线两两共面,则不一定共面,故D错误,
故选:ACD.
10.AB
【分析】利用向量的坐标运算解决平行垂直问题,利用向量法求线面角的余弦值.
【详解】是平行四边形,,又,
由,得,即,A选项正确;
,,又,则是平面的法向量,
即平面,在平面内射影为,
与平面的夹角为,,B选项正确;
,不是平面PBC的法向量,C选项错误;
,,无解,不成立,D选项错误.
故选:AB
11.AC
【分析】利用空间向量基本定理,结合空间向量数量积的运算性质和定义、空间向量夹角公式逐一判断即可.
【详解】以为空间一组基底,,
,
所以,A选项正确;
,所以
,
所以,B选项错误;
依题意可知,四边形ABCD是菱形,
所以,且,由于,,平面,
所以平面,C选项正确;
设直线与AC所成角为,,
,
,
,
,
所以,
,D选项错误.
故选:AC.
【点睛】关键点睛:本题的关键是利用空间向量基本定理、空间向量夹角公式.
12.
【分析】由向量垂直的性质计算即可得.
【详解】由,故,解得.
故答案为:.
13.
【分析】根据空间向量数量积的定义及运算律计算可得.
【详解】在正四面体中,,
又,,,
所以.
故答案为:
14./
【分析】根据题意,由线面角的计算公式,代入计算,即可得到结果.
【详解】设直线与平面所成角为,
则,
即直线与平面所成角的正弦值为.
故答案为:
15.(1)
(2)
【分析】(1)利用向量垂直、平行的条件即可求解;
(2)利用向量夹角公式求解即可.
【详解】(1)因为向量,所以,解得:,,
则,,
又因为,则,解得,
所以
(2)由(1)知,
所以,,
则,,,
即与所成角的余弦值
16.(1)
(2)
【分析】(1)利用向量的加减数乘运算,结合题设条件即可求得;
(2)先求出平面的基底两两之间的数量积,再根据(1)中的表示式,两边取平方,利用向量数量积的运算律计算即得.
【详解】(1)由图可得,;
(2)由题意,,
则,
于是,由两边取平方,
,
故.
17.(1)
(2)
【分析】(1)根据空间向量运算的坐标表示公式,结合空间向量模的坐标表示公式进行求解即可;
(2)根据空间向量坐标表示公式,结合空间向量垂直的坐标表示公式进行求解即可.
【详解】(1)因为向量,,
所以向量,,
因此,
所以;
(2)因为,,
所以,
因为点E在直线上,
所以设,
因为,所以,
因为,
所以,
所以,
因此点E的坐标.
18.(1)证明见解析
(2)
【分析】(1)根据面面平行的判定定理即可证明;
(2)根据向量法即可求二面角夹角的余弦值.
【详解】(1)
连接,
因为分别是的中点,P是与的交点,
所以为的中位线,所以,
又因为平面,平面,所以平面,
又因为且,所以四边形为平行四边形,所以,
因为平面,平面,所以平面,
又因为,所以平面平面;
(2)因为,,所以是等边三角形,
取的中点为,连接,则,,
又因为平面底面且交线为,所以底面,
因为,,,所以,
所以,所以,
所以取的三分之一等分点,,连接,则
以为坐标原点,以所在的直线为轴,以所在的直线为轴,以所在的直线为轴,建立如图所示的空间直角坐标系,
则,,
则,
设平面的法向量为,平面的法向量为,
,
令,则,所以,
同理可得,,
令,则,所以,
所以,
所以,
所以平面与平面夹角的余弦值.
19.(1)证明见解析
(2)
(3)H为线段PD的四等分点靠近P点
【分析】(1)利用线面平行的判定定理可得平面PDC,平面PDC,再由面面平行的判定定理可得答案;
(2)以D为原点,DA为x轴,DC为y轴,DP为z轴,建立空间直角坐标系,根据二面角的向量求法可求出结果;
(3)根据异面直线的向量公式可求出结果.
【详解】(1)四边形ABCD是正方形,
,平面PDC,平面PDC,
平面PDC,
四边形ADPQ是梯形,,平面PDC,平面PDC,
平面PDC,
平面ABQ,平面ABQ,,
平面平面DCP,
平面ABQ,平面PDC;
(2),即,,又,
以D为原点,DA,DC,DP所在直线分别为x轴、y轴、z轴,
建立空间直角坐标系,
则,,,,
,,,
设平面PBC的法向量,
则,
取,得,,得,
设平面PBQ的法向量,
则,
取,,,得,
设二面角的大小为,由图形得为钝角,
则,
为钝角,,
二面角的大小为,
平面CPB与平面PBQ所成角的大小为;
(3)点H在棱PD上,且异面直线AH与PB所成角的余弦值为,
设,,则,,
,,
,
解得,或舍去,线段DH的长为,又,
即,
H为线段PD的四等分点靠近P点.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第一章空间向量与立体几何同步过关练习卷-高二数学上学期人教A版(2019)选择性必修第一册
一、单选题
1.设,,,是半径为1的球的球面上的四个点.设,则不可能等于( )
A.3 B. C.4 D.
2.在三棱锥中,为的中点,则等于( )
A.-1 B.0 C.1 D.3
3.设向量,,不共面,已知,,,若A,C,D三点共线,则( )
A.1 B.2 C.3 D.4
4.下列说法正确的是( )
A.若向量、共线,则向量、所在的直线平行.
B.若、、是空间三个向量,则对空间任一向量,总存在唯一的有序实数组,使.
C.若向量、所在的直线是异面直线,则向量、一定不共线.
D.若三个向量、、两两共面,则三个向量、、一定共面.
5.已知四面体O-ABC,G1是△ABC的重心,G是OG1上一点,且OG=3GG1,若,则为( )
A. B.
C. D.
6.如图所示,在四棱柱中,底面为平行四边形,以顶点A为端点的三条棱长都为1,且两两夹角为,则的长为( )
A. B.2 C. D.
7.我国古代数学名著《九章算术》中,将底面为矩形且一侧棱垂直于底面的四棱锥称为阳马.如图,四棱锥为阳马,平面,且,,则( )
A. B.3 C.2 D.5
8.如图,在直三棱柱 中,所有棱长都相等,分别是棱 的中点,则异面直线与 所成角的余弦值是( )
A. B. C. D.
二、多选题
9.已知是空间中三个向量,则下列说法错误的是( )
A.对于空间中的任意一个向量,总存在实数,使得
B.若是空间的一个基底,则也是空间的一个基底
C.若,,则
D.若所在直线两两共面,则共面
10.已知点是平行四边形所在的平面外一点,如果,,,下列结论正确的有( )
A. B.与平面的夹角的余弦值为
C.是平面PBC的一个法向量 D.
11.如图,在平行六面体中,以顶点为端点的三条棱长都为1,且,则( )
A. B.
C.平面 D.直线与AC所成角的正弦值为
三、填空题
12.已知空间向量, 且,则 .
13.正四面体的棱长为2,设,,,则 .
14.已知平面的一个法向量,直线的方向向量,则直线与平面所成角的正弦值为 .
四、解答题
15.已知向量,向量,
(1)求向量,,的坐标;
(2)求与所成角的余弦值.
16.如图,四面体中,,分别为,上的点,且,,设,,.
(1)以为基底表示;
(2)若,且,,,求.
17.已知向量,,点,.
(1)求的值;
(2)在直线上存在一点E,使得,求点E的坐标.
18.如图,在三棱柱中,,,,平面底面,分别是的中点,P是与的交点.
(1)证明:平面平面;
(2)求平面与平面夹角的余弦值.
19.在如图所示的几何体中,四边形ABCD是正方形,四边形ADPQ是梯形,,,且.
(1)求证:平面PDC;
(2)求平面CPB与平面PBQ所成角的大小;
(3)已知点H在棱PD上,且异面直线AH与PB所成角的余弦值为,试确定点H的位置.
参考答案:
1.A
【分析】根据条件,得到,利用判断等号成立条件,确定不可能取的值.
【详解】因为,
且,所以,
而,当且仅当同向时,等号成立,
而A,,,在球面上,不可能共线,即不同向,
所以
且均小于直径长2,即,
综上,.
根据选项可知A不符合.
故选:A
2.C
【分析】由题意可得,再由数量积的运算律代入求解即可.
【详解】因为,
所以,
,
,
因为,
.
故选:C.
3.C
【分析】根据A,C,D三点共线,可得,则存在唯一实数,使得,再根据空间向量共线定理即可得解.
【详解】由,,
得,
因为A,C,D三点共线,所以,
则存在唯一实数,使得,
则,解得.
故选:C.
4.C
【分析】根据空间向量的相关概念以及空间向量基本定理分析判断.
【详解】对于A:若向量、共线,则向量、所在的直线平行或重合,故A错误;
对于B:根据空间向量基本定理可知,此时、、应是空间三个不共面的向量,故B错误;
对于C:反证:若向量、共线,则向量、所在的直线平行或重合,
这与向量、所在的直线是异面直线相矛盾,故C正确;
对于D:若三个向量、、两两共面,则三个向量、、不一定共面,
例如、、所在的直线为三棱锥的三条侧棱,故D错误;
故选:C.
5.A
【分析】连接AG1并延长,交BC于点E,利用向量加减、数乘几何意义用表示出,即可得答案.
【详解】如图所示,连接AG1并延长,交BC于点E,则点E为BC的中点,
,则,
由题设,,
所以.
故选:A
6.D
【分析】记,,,由,利用向量法即可求出的长.
【详解】解:记,,,
由题意可知,,
所以,
,
所以,即的长为,
故选:D.
7.B
【分析】根据题意建立空间直角坐标系计算求解即可.
【详解】因为平面,平面,
所以,
又因为四边形是矩形,所以,
以A为坐标原点,,,的方向分别为x,y,z轴的正方向建立如图所示的空间直角坐标系,
则,,则,
所以,,所以.
故选:B
8.D
【分析】利用平移法作出异面直线与 所成角,解三角形即可求得答案.
【详解】连接,因为在直三棱柱中,分别是棱的中点,
故,即四边形为平行四边形,所以,
则即为异面直线与 所成角或其补角;
直三棱柱中,所有棱长都相等,设其棱长为,连接,
则平面,故平面平面,
故,是棱的中点,故,
则,而
,又,故在中,,
由于异面直线所成角的范围,故异面直线与 所成角的余弦值是,
故选:D.
9.ACD
【分析】根据空间向量基本定理对选项一一判断即可得出答案.
【详解】对A,由空间向量基本定理,可知只有当不共面时,
才能作为基底,才能得到,故A错误;
对B,若是空间的一个基底,则不共面,
设,
则,因为无解,所以也不共面,
所以也是空间的一个基底,故B正确;
对C,若,,则不一定平行,故C错误;
对D,若所在直线两两共面,则不一定共面,故D错误,
故选:ACD.
10.AB
【分析】利用向量的坐标运算解决平行垂直问题,利用向量法求线面角的余弦值.
【详解】是平行四边形,,又,
由,得,即,A选项正确;
,,又,则是平面的法向量,
即平面,在平面内射影为,
与平面的夹角为,,B选项正确;
,不是平面PBC的法向量,C选项错误;
,,无解,不成立,D选项错误.
故选:AB
11.AC
【分析】利用空间向量基本定理,结合空间向量数量积的运算性质和定义、空间向量夹角公式逐一判断即可.
【详解】以为空间一组基底,,
,
所以,A选项正确;
,所以
,
所以,B选项错误;
依题意可知,四边形ABCD是菱形,
所以,且,由于,,平面,
所以平面,C选项正确;
设直线与AC所成角为,,
,
,
,
,
所以,
,D选项错误.
故选:AC.
【点睛】关键点睛:本题的关键是利用空间向量基本定理、空间向量夹角公式.
12.
【分析】由向量垂直的性质计算即可得.
【详解】由,故,解得.
故答案为:.
13.
【分析】根据空间向量数量积的定义及运算律计算可得.
【详解】在正四面体中,,
又,,,
所以.
故答案为:
14./
【分析】根据题意,由线面角的计算公式,代入计算,即可得到结果.
【详解】设直线与平面所成角为,
则,
即直线与平面所成角的正弦值为.
故答案为:
15.(1)
(2)
【分析】(1)利用向量垂直、平行的条件即可求解;
(2)利用向量夹角公式求解即可.
【详解】(1)因为向量,所以,解得:,,
则,,
又因为,则,解得,
所以
(2)由(1)知,
所以,,
则,,,
即与所成角的余弦值
16.(1)
(2)
【分析】(1)利用向量的加减数乘运算,结合题设条件即可求得;
(2)先求出平面的基底两两之间的数量积,再根据(1)中的表示式,两边取平方,利用向量数量积的运算律计算即得.
【详解】(1)由图可得,;
(2)由题意,,
则,
于是,由两边取平方,
,
故.
17.(1)
(2)
【分析】(1)根据空间向量运算的坐标表示公式,结合空间向量模的坐标表示公式进行求解即可;
(2)根据空间向量坐标表示公式,结合空间向量垂直的坐标表示公式进行求解即可.
【详解】(1)因为向量,,
所以向量,,
因此,
所以;
(2)因为,,
所以,
因为点E在直线上,
所以设,
因为,所以,
因为,
所以,
所以,
因此点E的坐标.
18.(1)证明见解析
(2)
【分析】(1)根据面面平行的判定定理即可证明;
(2)根据向量法即可求二面角夹角的余弦值.
【详解】(1)
连接,
因为分别是的中点,P是与的交点,
所以为的中位线,所以,
又因为平面,平面,所以平面,
又因为且,所以四边形为平行四边形,所以,
因为平面,平面,所以平面,
又因为,所以平面平面;
(2)因为,,所以是等边三角形,
取的中点为,连接,则,,
又因为平面底面且交线为,所以底面,
因为,,,所以,
所以,所以,
所以取的三分之一等分点,,连接,则
以为坐标原点,以所在的直线为轴,以所在的直线为轴,以所在的直线为轴,建立如图所示的空间直角坐标系,
则,,
则,
设平面的法向量为,平面的法向量为,
,
令,则,所以,
同理可得,,
令,则,所以,
所以,
所以,
所以平面与平面夹角的余弦值.
19.(1)证明见解析
(2)
(3)H为线段PD的四等分点靠近P点
【分析】(1)利用线面平行的判定定理可得平面PDC,平面PDC,再由面面平行的判定定理可得答案;
(2)以D为原点,DA为x轴,DC为y轴,DP为z轴,建立空间直角坐标系,根据二面角的向量求法可求出结果;
(3)根据异面直线的向量公式可求出结果.
【详解】(1)四边形ABCD是正方形,
,平面PDC,平面PDC,
平面PDC,
四边形ADPQ是梯形,,平面PDC,平面PDC,
平面PDC,
平面ABQ,平面ABQ,,
平面平面DCP,
平面ABQ,平面PDC;
(2),即,,又,
以D为原点,DA,DC,DP所在直线分别为x轴、y轴、z轴,
建立空间直角坐标系,
则,,,,
,,,
设平面PBC的法向量,
则,
取,得,,得,
设平面PBQ的法向量,
则,
取,,,得,
设二面角的大小为,由图形得为钝角,
则,
为钝角,,
二面角的大小为,
平面CPB与平面PBQ所成角的大小为;
(3)点H在棱PD上,且异面直线AH与PB所成角的余弦值为,
设,,则,,
,,
,
解得,或舍去,线段DH的长为,又,
即,
H为线段PD的四等分点靠近P点.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
