第12章 一次函数 单元检测(含答案)2023-2024学年沪科版数学八年级上册
文档属性
| 名称 | 第12章 一次函数 单元检测(含答案)2023-2024学年沪科版数学八年级上册 |
|
|
| 格式 | docx | ||
| 文件大小 | 361.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-18 00:00:00 | ||
图片预览



文档简介
第12章《一次函数》单元检测2023-2024学年八年级上册数学沪科版
一、单选题(共10小题,满分40分)
1.一次函数y=3x+1的图象一定经过( )
A. B. C. D.
2.我市春天经常刮风,如图,小明观测了4月6日连续个小时风力变化情况,并画出了风力随时间变化的图象,则下列说法正确的是( )
A.在8时至时,风力不断增大 B.8时风力最小
C.在8时至时,风力最大为5级 D.在时至时,风力最小为1级
3.如图,是一台自动测温记录仪的图象,它反映了我市某天气温(℃)随时间(时)变化而变化的关系,观察图象得到下列信息,其中正确的是( )
A.早上6时气温最低
B.下午14时气温是24℃
C.从0时至14时,气温随时间的推移而上升
D.从14时至24时,气温随时间的推移而下降
4.在某火车站托运物品时,不超过3kg的物品需付1.5元,以后每增加1kg(不足1kg按1kg计)需增加托运费0.5元,则下列图象能表示出托运费y与物品重量x之间的函数关系式的是( )
A. B.
C. D.
5.已知关于x的一次函数y=3x+n的图象如图,则关于x的一次方程3x+n=0的解是 ( )
A. B. C. D.
6.若点在函数的图象上,则的值为( )
A. B. C. D.
7.甲、乙两人相约从A地到B地,甲骑自行车先行,乙开车,两人均同一路线上速匀行驶,乙到B地后即停车等甲.甲、乙两人之间的距离y(千米)与甲行驶的时间x(小时)之间的函数关系如图所示,则乙从A地到B地所用的时间为( )
A.0.25小时 B.0.5小时 C.1小时 D.2.5小时
8.下列说法正确的是( )
A.一次函数是正比例函数
B.正比例函数是一次函数
C.不是正比例函数就一定不是一次函数
D.正比例函数不一定是一次函数
9.甲,乙两车在笔直的公路上行驶,乙车从之间的地出发,到达终点地停止行驶,甲车从起点A地与乙车同时出发到达地休息半小时后立即以另一速度返回地并停止行驶,在行驶过程中,两车均保持匀速,甲、乙两车相距的路程千米与乙车行驶的时间小时之间的关系如图所示,下列说法中正确的有( )
①甲车行驶的速度为每小时千米;
②两地之间的距离为千米;
③甲车返回地的速度为每小时千米;
④甲车返回地比乙车到地时间晚小时.
A.个 B.个
C.个 D.个
10.在平面直角坐标系中,点P的坐标为(a,b),点P的“变换点”P`的坐标定义如下:当时,P`点坐标为(a,-b);当时,P`点坐标为(b,-a).线段l:上所有点按上述“变换点”组成一个新的图形,若直线与组成的新的图形有两个交点,则k的取值范围是( )
A. B.或 C. D.
二、填空题(共8小题,满分32分)
11.已知与x成正比例,且时,y的值为7,求y与x的函数关系式 .
12.很多城市的网约车按里程收费:在一定的里程内按定额收费(起步价),超出规定里程部分按与超出里程的整千米数(不足1km的按1km计算)成正比例收费.江山市某网约车的起步价里程为2km,起步价为6元(不计等待时间).小明一次在该市乘车,从计费表上看到乘车里程和车费分别为4km,10元.如果你在该市乘坐某网约车的乘车里程为5km,那么需付车费 元.
13.一次函数的图像如图所示,当 时,.
14.如图,一次函数的图象经过点和点,若当时,对于的每一个值,总有函数的值大于一次函数的值,则的取值范围是 .
15.三角形三边的长分别为3,4,x,那么三角形的周长y与边长x的函数关系式是 ,x的取值范围是
16.等腰三角形的周长是16(cm),腰长为x(cm),底边长为y(cm),那么y与x之间的函数关系式是 (要求写出自变量x的取值范围).
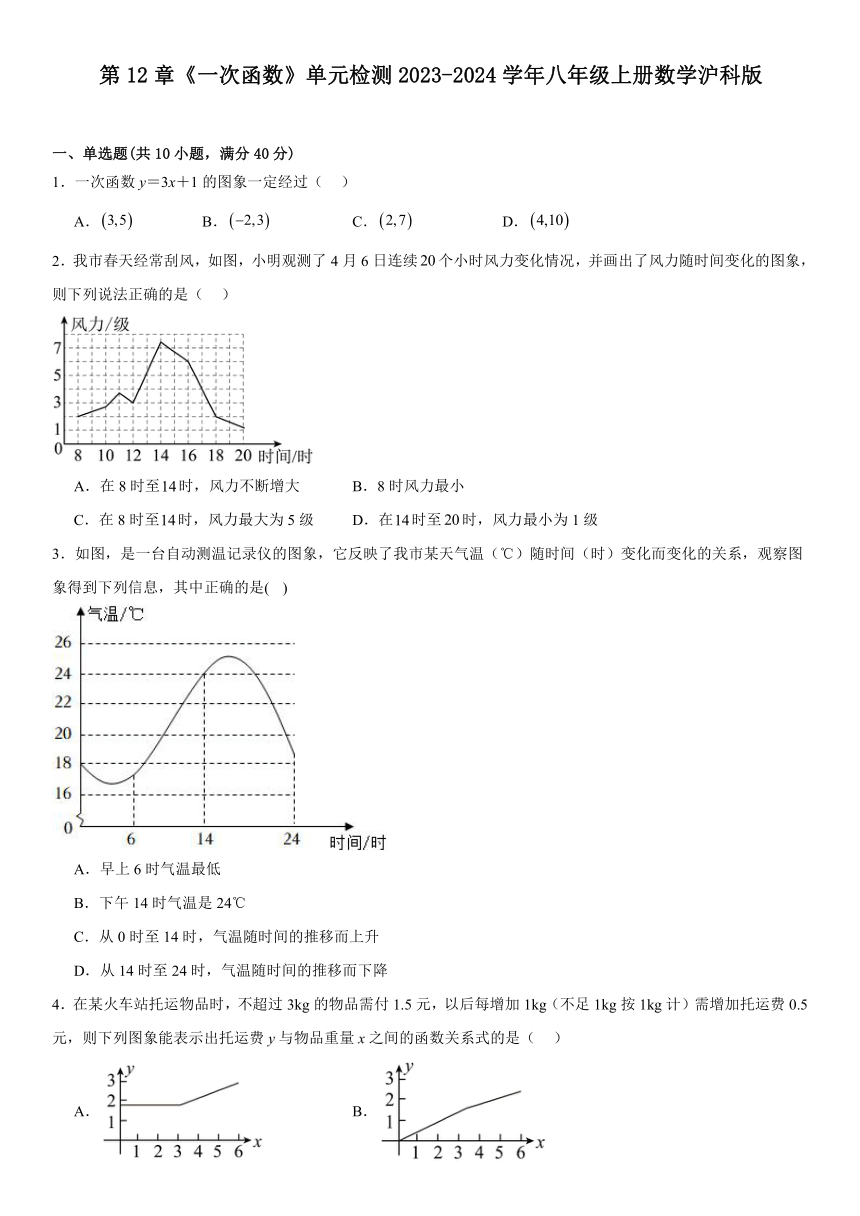
17.A、B两地相距480千米,甲车从A地匀速前往B地,乙车同时从B地沿同一公路匀速前往A地.甲车出发30分钟时发现自己有物件落在A地,于是立即掉头以原速返回取件,取件后立即掉头以原速继续匀速前行(掉头和取件时间忽略不计),两车之间相距的路程与甲车出发时间之间的函数关系如图所示.则当甲车到达B地时,乙车离A地的路程为 千米.
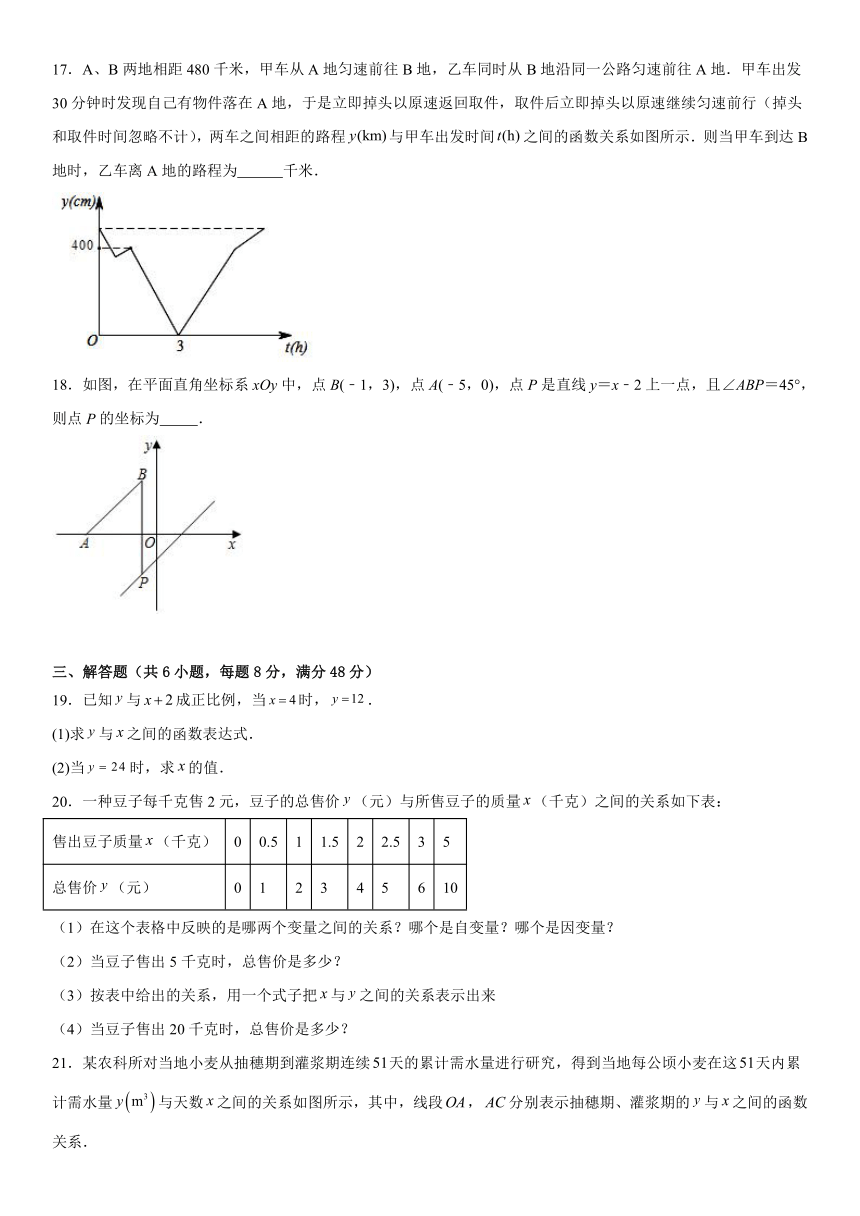
18.如图,在平面直角坐标系xOy中,点B(﹣1,3),点A(﹣5,0),点P是直线y=x﹣2上一点,且∠ABP=45°,则点P的坐标为 .
三、解答题(共6小题,每题8分,满分48分)
19.已知与成正比例,当时,.
(1)求与之间的函数表达式.
(2)当时,求的值.
20.一种豆子每千克售2元,豆子的总售价(元)与所售豆子的质量(千克)之间的关系如下表:
售出豆子质量(千克) 0 0.5 1 1.5 2 2.5 3 5
总售价(元) 0 1 2 3 4 5 6 10
(1)在这个表格中反映的是哪两个变量之间的关系?哪个是自变量?哪个是因变量?
(2)当豆子售出5千克时,总售价是多少?
(3)按表中给出的关系,用一个式子把与之间的关系表示出来
(4)当豆子售出20千克时,总售价是多少?
21.某农科所对当地小麦从抽穗期到灌浆期连续天的累计需水量进行研究,得到当地每公顷小麦在这天内累计需水量与天数之间的关系如图所示,其中,线段,分别表示抽穗期、灌浆期的与之间的函数关系.
(1)求这天内,与之间的函数关系式;
(2)求当地每公顷小麦在整个灌浆期的需水量.
22.为了预防新冠肺炎,某药店销售甲、乙两种防护口罩,已知甲种口罩每袋的售价比乙种口罩多元,小明从该药店购买了袋甲口罩和袋乙口罩共花费元.
(1)求该药店甲、乙两种口罩每袋的售价分别为多少元.
(2)根据消费者需求,该药店决定用不超过元购进甲、乙两种口罩共袋,已知甲种口罩每袋的进价为元,乙种口罩每袋的进价为元.若所购进口罩均可全部售出,请求出该药店所获利润(元)与甲种口罩的进货量(袋)之间的函数关系式.
(3)在(2)的前提下,要使药店获利最大,应该购进甲、乙两种口罩各多少袋,并求出最大利润.
23.如图,已知长方形OABC的顶点O在坐标原点,A、C分别在x、y轴的正半轴上,顶点B(8,6),直线y=﹣x+b经过点A交BC于D、交y轴于点M,点P是AD的中点,直线OP交AB于点E
(1)求点D的坐标及直线OP的解析式;
(2)求△ODP的面积,并在直线AD上找一点N,使△AEN的面积等于△ODP的面积,请求出点N的坐标.
(3)在x轴上有一点T(t,0)(5<t<8),过点T作x轴的垂线,分别交直线OE、AD于点F、G,在线段AE上是否存在一点Q,使得△FGQ为等腰直角三角形,若存在,请求出点Q的坐标及相应的t的值;若不存在,请说明理由.
24.如图,已知在平面直角坐标系中,的面积为18,,,点P的坐标是.
(1)求顶点A的坐标___________;
(2)若点P在第二象限,若的面积等于的面积,求出点P的坐标.
(3)在x轴上找一点D,使得为等腰三角形,直接写出点D 的坐标.
(4)求出当的值最小时点P的坐标.
参考答案:
1.C
2.D
3.B
4.D
5.D
6.D
7.B
8.B
9.B
10.A
11.
12.12
13.
14.
15. y=x+7 1<x<7
16.y=16-2x,4<x<8
17.
18.(﹣2,﹣4)
19.(1)
(2)
20.(1)总售价(元)与售出豆子的质量(千克),自变量是售出豆子的质量(千克),因变量是总售价(元);(2)元;(3);(4)元.
21.(1)
(2)
22.(1)甲、乙两种口罩每袋的售价分别为25元、20元;(2)W=a+1000;(3)购进甲、乙两种口罩各200袋时,药店获利最大,最大利润为1200元.
23.(1)点D的坐标为(2,6).直线OP的解析式为y=x.(2)点N的坐标为(3,5)或(13,-5).(3)在线段AE上存在一点Q,使得△FGQ为等腰直角三角形,当t=时点Q的坐标为(8,)或(8,),当t=时点Q的坐标为(8,).
24.(1)
(2)
(3)或或或
(4)
一、单选题(共10小题,满分40分)
1.一次函数y=3x+1的图象一定经过( )
A. B. C. D.
2.我市春天经常刮风,如图,小明观测了4月6日连续个小时风力变化情况,并画出了风力随时间变化的图象,则下列说法正确的是( )
A.在8时至时,风力不断增大 B.8时风力最小
C.在8时至时,风力最大为5级 D.在时至时,风力最小为1级
3.如图,是一台自动测温记录仪的图象,它反映了我市某天气温(℃)随时间(时)变化而变化的关系,观察图象得到下列信息,其中正确的是( )
A.早上6时气温最低
B.下午14时气温是24℃
C.从0时至14时,气温随时间的推移而上升
D.从14时至24时,气温随时间的推移而下降
4.在某火车站托运物品时,不超过3kg的物品需付1.5元,以后每增加1kg(不足1kg按1kg计)需增加托运费0.5元,则下列图象能表示出托运费y与物品重量x之间的函数关系式的是( )
A. B.
C. D.
5.已知关于x的一次函数y=3x+n的图象如图,则关于x的一次方程3x+n=0的解是 ( )
A. B. C. D.
6.若点在函数的图象上,则的值为( )
A. B. C. D.
7.甲、乙两人相约从A地到B地,甲骑自行车先行,乙开车,两人均同一路线上速匀行驶,乙到B地后即停车等甲.甲、乙两人之间的距离y(千米)与甲行驶的时间x(小时)之间的函数关系如图所示,则乙从A地到B地所用的时间为( )
A.0.25小时 B.0.5小时 C.1小时 D.2.5小时
8.下列说法正确的是( )
A.一次函数是正比例函数
B.正比例函数是一次函数
C.不是正比例函数就一定不是一次函数
D.正比例函数不一定是一次函数
9.甲,乙两车在笔直的公路上行驶,乙车从之间的地出发,到达终点地停止行驶,甲车从起点A地与乙车同时出发到达地休息半小时后立即以另一速度返回地并停止行驶,在行驶过程中,两车均保持匀速,甲、乙两车相距的路程千米与乙车行驶的时间小时之间的关系如图所示,下列说法中正确的有( )
①甲车行驶的速度为每小时千米;
②两地之间的距离为千米;
③甲车返回地的速度为每小时千米;
④甲车返回地比乙车到地时间晚小时.
A.个 B.个
C.个 D.个
10.在平面直角坐标系中,点P的坐标为(a,b),点P的“变换点”P`的坐标定义如下:当时,P`点坐标为(a,-b);当时,P`点坐标为(b,-a).线段l:上所有点按上述“变换点”组成一个新的图形,若直线与组成的新的图形有两个交点,则k的取值范围是( )
A. B.或 C. D.
二、填空题(共8小题,满分32分)
11.已知与x成正比例,且时,y的值为7,求y与x的函数关系式 .
12.很多城市的网约车按里程收费:在一定的里程内按定额收费(起步价),超出规定里程部分按与超出里程的整千米数(不足1km的按1km计算)成正比例收费.江山市某网约车的起步价里程为2km,起步价为6元(不计等待时间).小明一次在该市乘车,从计费表上看到乘车里程和车费分别为4km,10元.如果你在该市乘坐某网约车的乘车里程为5km,那么需付车费 元.
13.一次函数的图像如图所示,当 时,.
14.如图,一次函数的图象经过点和点,若当时,对于的每一个值,总有函数的值大于一次函数的值,则的取值范围是 .
15.三角形三边的长分别为3,4,x,那么三角形的周长y与边长x的函数关系式是 ,x的取值范围是
16.等腰三角形的周长是16(cm),腰长为x(cm),底边长为y(cm),那么y与x之间的函数关系式是 (要求写出自变量x的取值范围).
17.A、B两地相距480千米,甲车从A地匀速前往B地,乙车同时从B地沿同一公路匀速前往A地.甲车出发30分钟时发现自己有物件落在A地,于是立即掉头以原速返回取件,取件后立即掉头以原速继续匀速前行(掉头和取件时间忽略不计),两车之间相距的路程与甲车出发时间之间的函数关系如图所示.则当甲车到达B地时,乙车离A地的路程为 千米.
18.如图,在平面直角坐标系xOy中,点B(﹣1,3),点A(﹣5,0),点P是直线y=x﹣2上一点,且∠ABP=45°,则点P的坐标为 .
三、解答题(共6小题,每题8分,满分48分)
19.已知与成正比例,当时,.
(1)求与之间的函数表达式.
(2)当时,求的值.
20.一种豆子每千克售2元,豆子的总售价(元)与所售豆子的质量(千克)之间的关系如下表:
售出豆子质量(千克) 0 0.5 1 1.5 2 2.5 3 5
总售价(元) 0 1 2 3 4 5 6 10
(1)在这个表格中反映的是哪两个变量之间的关系?哪个是自变量?哪个是因变量?
(2)当豆子售出5千克时,总售价是多少?
(3)按表中给出的关系,用一个式子把与之间的关系表示出来
(4)当豆子售出20千克时,总售价是多少?
21.某农科所对当地小麦从抽穗期到灌浆期连续天的累计需水量进行研究,得到当地每公顷小麦在这天内累计需水量与天数之间的关系如图所示,其中,线段,分别表示抽穗期、灌浆期的与之间的函数关系.
(1)求这天内,与之间的函数关系式;
(2)求当地每公顷小麦在整个灌浆期的需水量.
22.为了预防新冠肺炎,某药店销售甲、乙两种防护口罩,已知甲种口罩每袋的售价比乙种口罩多元,小明从该药店购买了袋甲口罩和袋乙口罩共花费元.
(1)求该药店甲、乙两种口罩每袋的售价分别为多少元.
(2)根据消费者需求,该药店决定用不超过元购进甲、乙两种口罩共袋,已知甲种口罩每袋的进价为元,乙种口罩每袋的进价为元.若所购进口罩均可全部售出,请求出该药店所获利润(元)与甲种口罩的进货量(袋)之间的函数关系式.
(3)在(2)的前提下,要使药店获利最大,应该购进甲、乙两种口罩各多少袋,并求出最大利润.
23.如图,已知长方形OABC的顶点O在坐标原点,A、C分别在x、y轴的正半轴上,顶点B(8,6),直线y=﹣x+b经过点A交BC于D、交y轴于点M,点P是AD的中点,直线OP交AB于点E
(1)求点D的坐标及直线OP的解析式;
(2)求△ODP的面积,并在直线AD上找一点N,使△AEN的面积等于△ODP的面积,请求出点N的坐标.
(3)在x轴上有一点T(t,0)(5<t<8),过点T作x轴的垂线,分别交直线OE、AD于点F、G,在线段AE上是否存在一点Q,使得△FGQ为等腰直角三角形,若存在,请求出点Q的坐标及相应的t的值;若不存在,请说明理由.
24.如图,已知在平面直角坐标系中,的面积为18,,,点P的坐标是.
(1)求顶点A的坐标___________;
(2)若点P在第二象限,若的面积等于的面积,求出点P的坐标.
(3)在x轴上找一点D,使得为等腰三角形,直接写出点D 的坐标.
(4)求出当的值最小时点P的坐标.
参考答案:
1.C
2.D
3.B
4.D
5.D
6.D
7.B
8.B
9.B
10.A
11.
12.12
13.
14.
15. y=x+7 1<x<7
16.y=16-2x,4<x<8
17.
18.(﹣2,﹣4)
19.(1)
(2)
20.(1)总售价(元)与售出豆子的质量(千克),自变量是售出豆子的质量(千克),因变量是总售价(元);(2)元;(3);(4)元.
21.(1)
(2)
22.(1)甲、乙两种口罩每袋的售价分别为25元、20元;(2)W=a+1000;(3)购进甲、乙两种口罩各200袋时,药店获利最大,最大利润为1200元.
23.(1)点D的坐标为(2,6).直线OP的解析式为y=x.(2)点N的坐标为(3,5)或(13,-5).(3)在线段AE上存在一点Q,使得△FGQ为等腰直角三角形,当t=时点Q的坐标为(8,)或(8,),当t=时点Q的坐标为(8,).
24.(1)
(2)
(3)或或或
(4)
