第21章《二次函数与反比例函数》单元检测题(含答案) 2023-2024学年沪科版九年级数学上册
文档属性
| 名称 | 第21章《二次函数与反比例函数》单元检测题(含答案) 2023-2024学年沪科版九年级数学上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 450.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-18 00:00:00 | ||
图片预览



文档简介
第21章《二次函数与反比例函数》单元检测题
2023-2024学年九年级上册数学沪科版
一、单选题(共10小题,满分40分)
1.反比例函数一定经过的点是( )
A. B. C. D.
2.若抛物线与x轴的两个交点坐标是和,则抛物线的对称轴是( )
A. B. C. D.
3.若点A(1,y1)、B(2,y2)都在反比例函数的图象上,则y1、y2的大小关系为
A.y1<y2 B.y1≤y2 C.y1>y2 D.y1≥y2
4.二次函数y=ax2+bx-1(a≠0)的图象经过点(1,1).则代数式1-a-b的值为( )
A.-3 B.-1 C.2 D.5
5.如图,二次函数的图象与x轴交于,B两点,下列说法错误的是( )
A.该函数图象的顶点坐标为
B.若为该图象上两点,则
C.方程有两个不相等的实数根
D.当时,y随x的增大而增大
6.把抛物线向上平移2个单位长度,则平移后抛物线的解析式是( )
A. B. C. D.
7.二次函数 的图象如图所示,有下列结论:
①;
②若 是抛物线上的两点,则 ,
③;
④对于任意实数m,都有
其中正确的个数有( )
A.1个 B.2个 C.3个 D.4个
8.已知:二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论中:①abc>0;②2a+b<0;③a-b+c<0;④当x>1时,y随x的增大而增大;⑤a>1,其中正确的项是( )
A.①②⑤ B.①④⑤ C.①③⑤ D.②③④
9.已知点A、B分别在反比例函数(x>0),(x>0)的图象上,且∠AOB=90°,则∠B=30°,则k的取值为( )
A. B. C.﹣2 D.﹣3
10.如图,在中,,是的中点,,动点从点出发沿向终点运动,动点从点出发沿折线向终点运动,两点速度均为每秒1个单位,两点同时出发,当其中一点到达终点后,运动停止,设运动时间为,的面积为(平方单位),则与之间的图象大致为( )
A. B. C. D.
二、填空题(共8小题,满分32分)
11.将抛物线向右移3单位,上移2单位所得到的新抛物线解析式为 .
12.已知二次函数的图像上有三个点.用“,,”连接的结果是 .
13.在平整的路面上某型号汽车急刹车后仍将滑行的距离s(米)与刹车的速度v(千米/时)有这样的关系,当汽车紧急刹车仍滑行27米时,汽车刹车前的速度是 千米/时.
14.如图,点A在反比例函数的图象上,点B在x轴的正半轴上,若,则的面积为 .
15.如图,M为双曲线()上的一点,分别交直线于点D、C两点.若直线与y轴交于点A,与x轴交于点B,则的值为 .
16.设抛物线l:的顶点为D,与y轴的交点是C,我们称以C为顶点,且过点D的抛物线为抛物线l的“伴随抛物线”,请写出抛物线的伴随抛物线的解析式 .
17.已知抛物线y=ax2+bx+c(a,b,c是常数),a+b+c=0.下列四个结论:
①抛物线与x轴一定有两个不同的交点;
②若抛物线经过点(-1,0),则b=0;
③若b=c,则方程ax2+bx+c=0一定有根x=-2;
④点A(x1,y1),B(x1,y1)在抛物线上,若0<a<c,则当x1>x2>1时,y1>y2.
其中正确的是 (填写序号).
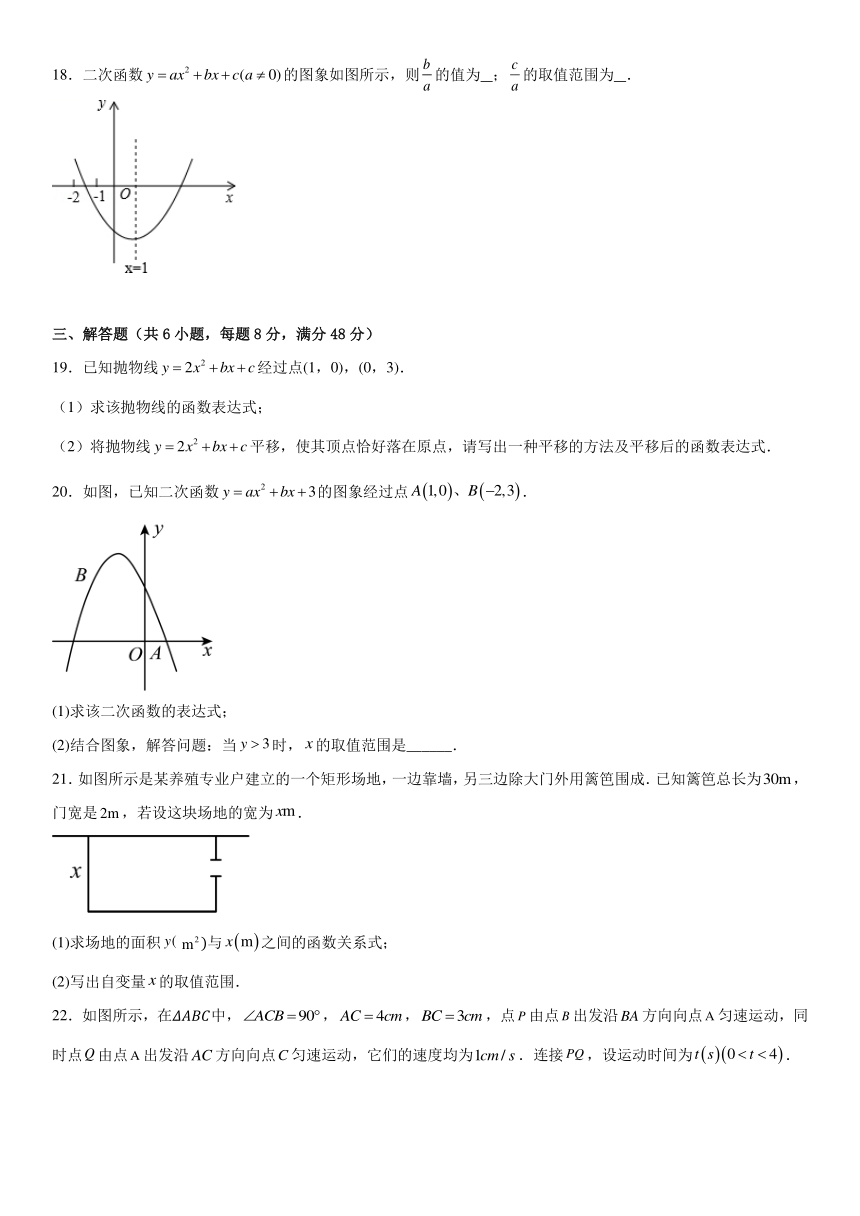
18.二次函数的图象如图所示,则的值为 ;的取值范围为 .
三、解答题(共6小题,每题8分,满分48分)
19.已知抛物线经过点(1,0),(0,3).
(1)求该抛物线的函数表达式;
(2)将抛物线平移,使其顶点恰好落在原点,请写出一种平移的方法及平移后的函数表达式.
20.如图,已知二次函数的图象经过点.
(1)求该二次函数的表达式;
(2)结合图象,解答问题:当时,的取值范围是______.
21.如图所示是某养殖专业户建立的一个矩形场地,一边靠墙,另三边除大门外用篱笆围成.已知篱笆总长为,门宽是,若设这块场地的宽为.
(1)求场地的面积与之间的函数关系式;
(2)写出自变量的取值范围.
22.如图所示,在中,,,,点由点出发沿方向向点匀速运动,同时点由点出发沿方向向点匀速运动,它们的速度均为.连接,设运动时间为.
(1)当为何值时,?
(2)设的面积为,求与的函数关系式,并求出当为何值时,取得最大值?的最大值是多少?
23.如图,小明用一个固定电压为的蓄电池,通过调节滑动变阻器来改变电流大小,完成控制灯泡(灯丝的电阻值)亮度的实验.
(1)写出电路中电流与可变电阻的函数关系式;
(2)在平面直角坐标系中画出(1)的函数图象;
(3)根据图象特征写一条函数的性质.
24.如图,已知正比例函数和反比例函数的图像交于点.
(1)求反比例函数的表达式;
(2)观察图像,直接写出当时,自变量的取值范围;
(3)将直线沿轴向上平移,使平移后的直线与轴交于,与双曲线在第一象限内交于点,求点的坐标.
参考答案:
1.B
2.D
3.C
4.B
5.D
6.C
7.A
8.B
9.D
10.A
11.
12./
13.
14.3
15.6
16.
17.②
18. -2;
19.(1);(2)将抛物线向左平移个单位,向上平移个单位,解析式变为.
20.(1)
(2)
21.(1)
(2)
22.(1)(2)S= (t )2+, t=,S有最大值,最大值为.
23.(1)
(2)11
(3)函数值随着自变量的增大而减小
24.(1)
(2)或
(3)
2023-2024学年九年级上册数学沪科版
一、单选题(共10小题,满分40分)
1.反比例函数一定经过的点是( )
A. B. C. D.
2.若抛物线与x轴的两个交点坐标是和,则抛物线的对称轴是( )
A. B. C. D.
3.若点A(1,y1)、B(2,y2)都在反比例函数的图象上,则y1、y2的大小关系为
A.y1<y2 B.y1≤y2 C.y1>y2 D.y1≥y2
4.二次函数y=ax2+bx-1(a≠0)的图象经过点(1,1).则代数式1-a-b的值为( )
A.-3 B.-1 C.2 D.5
5.如图,二次函数的图象与x轴交于,B两点,下列说法错误的是( )
A.该函数图象的顶点坐标为
B.若为该图象上两点,则
C.方程有两个不相等的实数根
D.当时,y随x的增大而增大
6.把抛物线向上平移2个单位长度,则平移后抛物线的解析式是( )
A. B. C. D.
7.二次函数 的图象如图所示,有下列结论:
①;
②若 是抛物线上的两点,则 ,
③;
④对于任意实数m,都有
其中正确的个数有( )
A.1个 B.2个 C.3个 D.4个
8.已知:二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论中:①abc>0;②2a+b<0;③a-b+c<0;④当x>1时,y随x的增大而增大;⑤a>1,其中正确的项是( )
A.①②⑤ B.①④⑤ C.①③⑤ D.②③④
9.已知点A、B分别在反比例函数(x>0),(x>0)的图象上,且∠AOB=90°,则∠B=30°,则k的取值为( )
A. B. C.﹣2 D.﹣3
10.如图,在中,,是的中点,,动点从点出发沿向终点运动,动点从点出发沿折线向终点运动,两点速度均为每秒1个单位,两点同时出发,当其中一点到达终点后,运动停止,设运动时间为,的面积为(平方单位),则与之间的图象大致为( )
A. B. C. D.
二、填空题(共8小题,满分32分)
11.将抛物线向右移3单位,上移2单位所得到的新抛物线解析式为 .
12.已知二次函数的图像上有三个点.用“,,”连接的结果是 .
13.在平整的路面上某型号汽车急刹车后仍将滑行的距离s(米)与刹车的速度v(千米/时)有这样的关系,当汽车紧急刹车仍滑行27米时,汽车刹车前的速度是 千米/时.
14.如图,点A在反比例函数的图象上,点B在x轴的正半轴上,若,则的面积为 .
15.如图,M为双曲线()上的一点,分别交直线于点D、C两点.若直线与y轴交于点A,与x轴交于点B,则的值为 .
16.设抛物线l:的顶点为D,与y轴的交点是C,我们称以C为顶点,且过点D的抛物线为抛物线l的“伴随抛物线”,请写出抛物线的伴随抛物线的解析式 .
17.已知抛物线y=ax2+bx+c(a,b,c是常数),a+b+c=0.下列四个结论:
①抛物线与x轴一定有两个不同的交点;
②若抛物线经过点(-1,0),则b=0;
③若b=c,则方程ax2+bx+c=0一定有根x=-2;
④点A(x1,y1),B(x1,y1)在抛物线上,若0<a<c,则当x1>x2>1时,y1>y2.
其中正确的是 (填写序号).
18.二次函数的图象如图所示,则的值为 ;的取值范围为 .
三、解答题(共6小题,每题8分,满分48分)
19.已知抛物线经过点(1,0),(0,3).
(1)求该抛物线的函数表达式;
(2)将抛物线平移,使其顶点恰好落在原点,请写出一种平移的方法及平移后的函数表达式.
20.如图,已知二次函数的图象经过点.
(1)求该二次函数的表达式;
(2)结合图象,解答问题:当时,的取值范围是______.
21.如图所示是某养殖专业户建立的一个矩形场地,一边靠墙,另三边除大门外用篱笆围成.已知篱笆总长为,门宽是,若设这块场地的宽为.
(1)求场地的面积与之间的函数关系式;
(2)写出自变量的取值范围.
22.如图所示,在中,,,,点由点出发沿方向向点匀速运动,同时点由点出发沿方向向点匀速运动,它们的速度均为.连接,设运动时间为.
(1)当为何值时,?
(2)设的面积为,求与的函数关系式,并求出当为何值时,取得最大值?的最大值是多少?
23.如图,小明用一个固定电压为的蓄电池,通过调节滑动变阻器来改变电流大小,完成控制灯泡(灯丝的电阻值)亮度的实验.
(1)写出电路中电流与可变电阻的函数关系式;
(2)在平面直角坐标系中画出(1)的函数图象;
(3)根据图象特征写一条函数的性质.
24.如图,已知正比例函数和反比例函数的图像交于点.
(1)求反比例函数的表达式;
(2)观察图像,直接写出当时,自变量的取值范围;
(3)将直线沿轴向上平移,使平移后的直线与轴交于,与双曲线在第一象限内交于点,求点的坐标.
参考答案:
1.B
2.D
3.C
4.B
5.D
6.C
7.A
8.B
9.D
10.A
11.
12./
13.
14.3
15.6
16.
17.②
18. -2;
19.(1);(2)将抛物线向左平移个单位,向上平移个单位,解析式变为.
20.(1)
(2)
21.(1)
(2)
22.(1)(2)S= (t )2+, t=,S有最大值,最大值为.
23.(1)
(2)11
(3)函数值随着自变量的增大而减小
24.(1)
(2)或
(3)
