第十二章全等三角形 单元练习(无答案)2024-2025学年人教版数学八年级上册
文档属性
| 名称 | 第十二章全等三角形 单元练习(无答案)2024-2025学年人教版数学八年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 326.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-19 09:08:32 | ||
图片预览

文档简介
第十二章全等三角形 章节检测2024-2025学年人教版数学八年级上册
一、单选题
1.如图,是尺规作图中“画一个角等于已知角”的示意图,该作法运用了“全等三角形的对应角相等”这一性质,则判定图中两三角形全等的条件是( ) .
A.SAS B.ASA C.AAS D.SSS
2.如图,,,,以下四个结论:①;②;③;④CD平分.其中结论正确的个数是( )
A.1 B.2 C.3 D.4
3.如图,已知,与交于点O,添加一个适当的条件后,仍不能使得成立的是( )
A. B. C. D.
4.如图,在△ABC中,∠ACB=90°,BE平分∠ABC,ED⊥AB于D,如果AC=5cm,那么AE+DE等于 ( )
A.3cm B.4cm C.5cm D.6cm
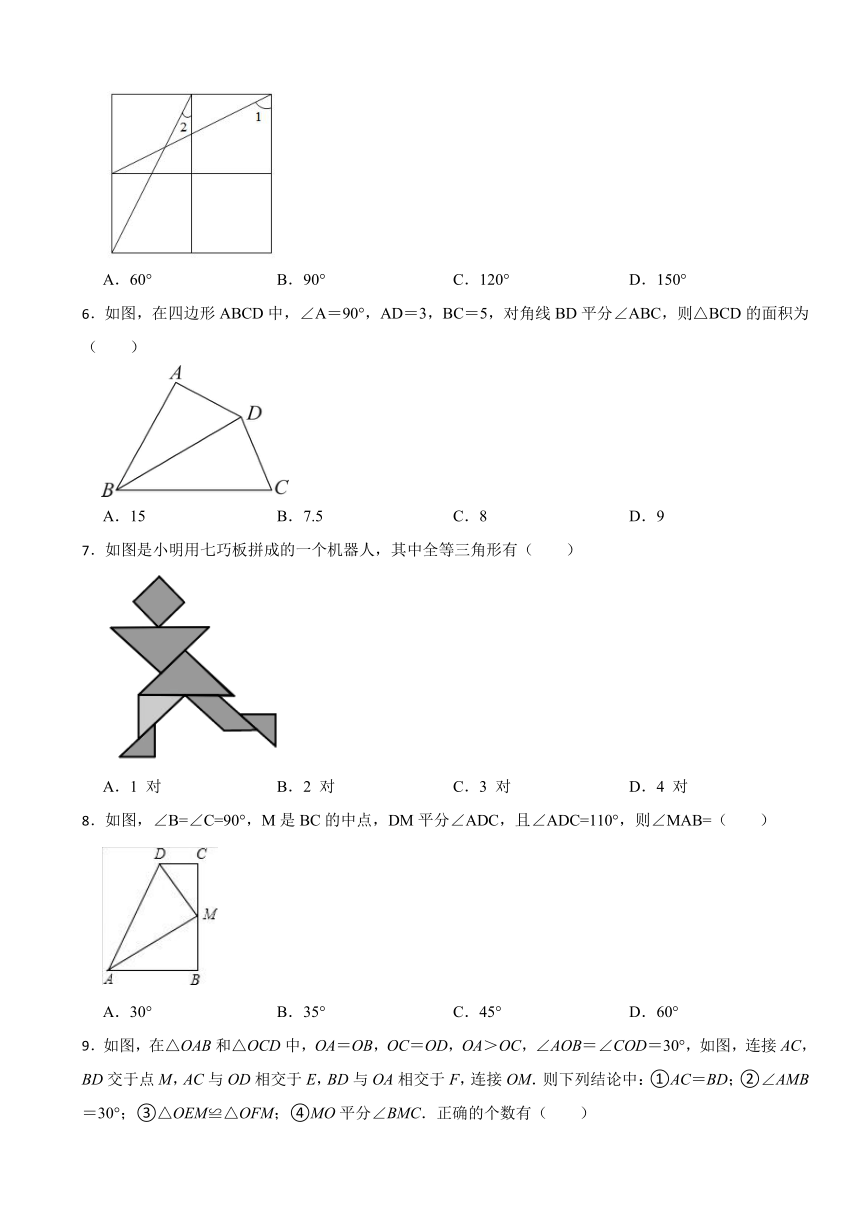
5.如图,已知方格纸中是4个相同的正方形,则( )
A.60° B.90° C.120° D.150°
6.如图,在四边形ABCD中,∠A=90°,AD=3,BC=5,对角线BD平分∠ABC,则△BCD的面积为( )
A.15 B.7.5 C.8 D.9
7.如图是小明用七巧板拼成的一个机器人,其中全等三角形有( )
A.1 对 B.2 对 C.3 对 D.4 对
8.如图,∠B=∠C=90°,M是BC的中点,DM平分∠ADC,且∠ADC=110°,则∠MAB=( )
A.30° B.35° C.45° D.60°
9.如图,在△OAB和△OCD中,OA=OB,OC=OD,OA>OC,∠AOB=∠COD=30°,如图,连接AC,BD交于点M,AC与OD相交于E,BD与OA相交于F,连接OM.则下列结论中:①AC=BD;②∠AMB=30°;③△OEM≌△OFM;④MO平分∠BMC.正确的个数有( )
A.1个 B.2个 C.3个 D.4个
10.如图,在四边形ABCD中,BD平分∠ABC,CD⊥BD于点D,AC=5,BC-AB=2,则△ADC面积的最大值为( )
A.2 B.2.5 C.4 D.5
二、填空题
11.如图,,射线在外,且,若平分,平分,则 .
12.如图,AD∥BC,AD=BC,请你添加一个条件: ,使△ADE≌△CBF.(写出一个条件即可)
13.点O是△ABC内一点,且点O到三边的距离相等,∠A=70°,则∠BOC的度数为 .
14.等腰三角形ABC中,AB=AC,D、E分别是AC、AB上两点,连结BD、CE,BD=CE,且BC>BD,∠A=48°,∠BCE=36°,则∠ADB的度数等于 。
三、解答题
15.如图,点、在直线上,,平分,,求的度数.
16.如图,,以O为顶点,为一边画,分别平分与.
(1)如图1,若射线在内部,锐角,则____;
(2)如图2,若射线在外部,锐角,求的度数;
(3)将问题(2)中“锐角”改为“为任意大小的钝角”,其余条件不变,能否求出的度数?若能,求出的度数;若不能,说明理由.
17.某游乐场有两个长度相同的滑梯,要想使左边滑梯BC的高度AC与右边滑梯EF的水平方向的长度DF相等,则两个滑梯的倾斜角∠ABC与∠DFE的大小必须满足什么关系?说明理由.
18.如图,点F在线段AB上,点E,G在线段CD上,AB∥CD,∠1=∠2.
(1)求证:FG∥AE;
(2)若FG⊥BC于点H,BC平分∠ABD,∠D=120°,求∠1的度数.
19.如图(1),AB⊥AD,ED⊥AD,AB=CD,AC=DE,试说明BC⊥CE的理由;
如图(2),若△ABC向右平移,使得点C移到点D,AB⊥AD,ED⊥AD,AB=CD,AD=DE,探索BD⊥CE的结论是否成立,并说明理由.
20.如图所示,在△ABC中,AE是角平分线,AD是高,∠BAC=80°,∠EAD=10°,求∠B的度数
21.认真阅读下面关于三角形内外角平分线所夹角的探究片段,完成所提出的问题.
探究1:如图l,在△ABC中,O是∠ABC与∠ACB的平分线BO和CO的交点,通过分析发现∠BOC=90+∠A,理由如下:
∵BO和CO分别是∠ABC和∠ACB的角平分线
∴∠1=∠ABC, ∠2=∠ACB
∴∠l+∠2=(∠ABC+∠ACB)= (180-∠A)= 90-∠A
∴∠BOC=180-(∠1+∠2) =180-(90-∠A)=90+∠A
(1)探究2;如图2中,O是∠ABC与外角∠ACD的平分线BO和CO的交点,试分析∠BOC与∠A有怎样的关系?请说明理由.
(2)探究3:如图3中, O是外角∠DBC与外角∠ECB的平分线BO和CO的交点,则∠BOC与∠A有怎样的关系?(直接写出结论)
(3)拓展:如图4,在四边形ABCD中,O是∠ABC与∠DCB的平分线BO和CO的交点,则∠BOC与∠A+∠D有怎样的关系?(直接写出结论)
一、单选题
1.如图,是尺规作图中“画一个角等于已知角”的示意图,该作法运用了“全等三角形的对应角相等”这一性质,则判定图中两三角形全等的条件是( ) .
A.SAS B.ASA C.AAS D.SSS
2.如图,,,,以下四个结论:①;②;③;④CD平分.其中结论正确的个数是( )
A.1 B.2 C.3 D.4
3.如图,已知,与交于点O,添加一个适当的条件后,仍不能使得成立的是( )
A. B. C. D.
4.如图,在△ABC中,∠ACB=90°,BE平分∠ABC,ED⊥AB于D,如果AC=5cm,那么AE+DE等于 ( )
A.3cm B.4cm C.5cm D.6cm
5.如图,已知方格纸中是4个相同的正方形,则( )
A.60° B.90° C.120° D.150°
6.如图,在四边形ABCD中,∠A=90°,AD=3,BC=5,对角线BD平分∠ABC,则△BCD的面积为( )
A.15 B.7.5 C.8 D.9
7.如图是小明用七巧板拼成的一个机器人,其中全等三角形有( )
A.1 对 B.2 对 C.3 对 D.4 对
8.如图,∠B=∠C=90°,M是BC的中点,DM平分∠ADC,且∠ADC=110°,则∠MAB=( )
A.30° B.35° C.45° D.60°
9.如图,在△OAB和△OCD中,OA=OB,OC=OD,OA>OC,∠AOB=∠COD=30°,如图,连接AC,BD交于点M,AC与OD相交于E,BD与OA相交于F,连接OM.则下列结论中:①AC=BD;②∠AMB=30°;③△OEM≌△OFM;④MO平分∠BMC.正确的个数有( )
A.1个 B.2个 C.3个 D.4个
10.如图,在四边形ABCD中,BD平分∠ABC,CD⊥BD于点D,AC=5,BC-AB=2,则△ADC面积的最大值为( )
A.2 B.2.5 C.4 D.5
二、填空题
11.如图,,射线在外,且,若平分,平分,则 .
12.如图,AD∥BC,AD=BC,请你添加一个条件: ,使△ADE≌△CBF.(写出一个条件即可)
13.点O是△ABC内一点,且点O到三边的距离相等,∠A=70°,则∠BOC的度数为 .
14.等腰三角形ABC中,AB=AC,D、E分别是AC、AB上两点,连结BD、CE,BD=CE,且BC>BD,∠A=48°,∠BCE=36°,则∠ADB的度数等于 。
三、解答题
15.如图,点、在直线上,,平分,,求的度数.
16.如图,,以O为顶点,为一边画,分别平分与.
(1)如图1,若射线在内部,锐角,则____;
(2)如图2,若射线在外部,锐角,求的度数;
(3)将问题(2)中“锐角”改为“为任意大小的钝角”,其余条件不变,能否求出的度数?若能,求出的度数;若不能,说明理由.
17.某游乐场有两个长度相同的滑梯,要想使左边滑梯BC的高度AC与右边滑梯EF的水平方向的长度DF相等,则两个滑梯的倾斜角∠ABC与∠DFE的大小必须满足什么关系?说明理由.
18.如图,点F在线段AB上,点E,G在线段CD上,AB∥CD,∠1=∠2.
(1)求证:FG∥AE;
(2)若FG⊥BC于点H,BC平分∠ABD,∠D=120°,求∠1的度数.
19.如图(1),AB⊥AD,ED⊥AD,AB=CD,AC=DE,试说明BC⊥CE的理由;
如图(2),若△ABC向右平移,使得点C移到点D,AB⊥AD,ED⊥AD,AB=CD,AD=DE,探索BD⊥CE的结论是否成立,并说明理由.
20.如图所示,在△ABC中,AE是角平分线,AD是高,∠BAC=80°,∠EAD=10°,求∠B的度数
21.认真阅读下面关于三角形内外角平分线所夹角的探究片段,完成所提出的问题.
探究1:如图l,在△ABC中,O是∠ABC与∠ACB的平分线BO和CO的交点,通过分析发现∠BOC=90+∠A,理由如下:
∵BO和CO分别是∠ABC和∠ACB的角平分线
∴∠1=∠ABC, ∠2=∠ACB
∴∠l+∠2=(∠ABC+∠ACB)= (180-∠A)= 90-∠A
∴∠BOC=180-(∠1+∠2) =180-(90-∠A)=90+∠A
(1)探究2;如图2中,O是∠ABC与外角∠ACD的平分线BO和CO的交点,试分析∠BOC与∠A有怎样的关系?请说明理由.
(2)探究3:如图3中, O是外角∠DBC与外角∠ECB的平分线BO和CO的交点,则∠BOC与∠A有怎样的关系?(直接写出结论)
(3)拓展:如图4,在四边形ABCD中,O是∠ABC与∠DCB的平分线BO和CO的交点,则∠BOC与∠A+∠D有怎样的关系?(直接写出结论)
