组合图形的面积(综合练习)(含答案)-2024-2025学年五年级上册数学人教版
文档属性
| 名称 | 组合图形的面积(综合练习)(含答案)-2024-2025学年五年级上册数学人教版 |  | |
| 格式 | docx | ||
| 文件大小 | 805.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-18 20:01:06 | ||
图片预览

文档简介
组合图形的面积 经典例题
班级 小组 姓名 成绩 (满分 120)
一、组合图形的面积
(一)组合图形的面积计算(共 4 小题,每题 3 分,共计 12 分)
例 1. 求下面图形的面积。 (单位:cm)
例 1. 变式 1. 先回答问题,再计算图形的面积。 (单位:cm)
(1)
组合图形的面积= ( )面积+( )面积
(2)
52
阴影部分的面积= ( )面积- ( )面积
例 1. 变式 2. 计算下面图形的面积,你能用不同的计算方法吗
第 1 页 共 10 页
组合图形的面积 经典例题
例 1. 变式 3. 如图,左边阴影部分的面积是 60 平方厘米。求右边空白部分(梯形)的面积。(单
位:厘米)
(二)组合图形的面积计算(共 4 小题,每题 3 分,共计 12 分)
例 2. 计算下列组合图形的面积。 (单位:cm)
例 2. 变式 1. 解决问题。
下图是一间房子侧面的墙,它的面积是多少 如果每平方米用 120 块砖,砌这面墙一共需要多
少块砖
第 2 页 共 10 页
组合图形的面积 经典例题
例 2. 变式 2. 下图是一块地的平面图,求它的面积。 (单位:米)
例 2. 变式 3. 求下图中的阴影部分的面积。 (单位:cm)
二、成长的脚印
(三)估计不规则图形的面积(共 4 小题,每题 3 分,共计 12 分)
例 3. 想一想,填一填。
估计不规则图形的面积的方法是根据图形的形状,确定一个近似的( ),通过对( )的
计算,估计出不规则图形的面积。
例 3. 变式 1. 估算运动场地在图上的面积。 (小方格的边长为 1 cm)
面积约为: cm 。
第 3 页 共 10 页
组合图形的面积 经典例题
例 3. 变式 2. 某公司想购买土地(如图所示)。比一比,在同等价格下购买哪一块划算些
(每个方格 1 km )
例 3. 变式 3. 如图,这是教室的一面墙壁,学校要涂上白色涂料(黑板和墙裙除外)。如果每平
方米需要花费 3.5 元,那么粉刷这样的 20 面墙壁一共需要多少元 (单位:米)
(四)估计不规则图形的面积(共 4 小题,每题 3 分,共计 12 分)
例 4. 一条白色的正方形手帕,它的边长是 18 cm ,手帕上横竖各有两道灰条(如下图所示阴影
部分),灰条宽是 2 cm。这条手帕白色部分的面积是多少
第 4 页 共 10 页
组合图形的面积 经典例题
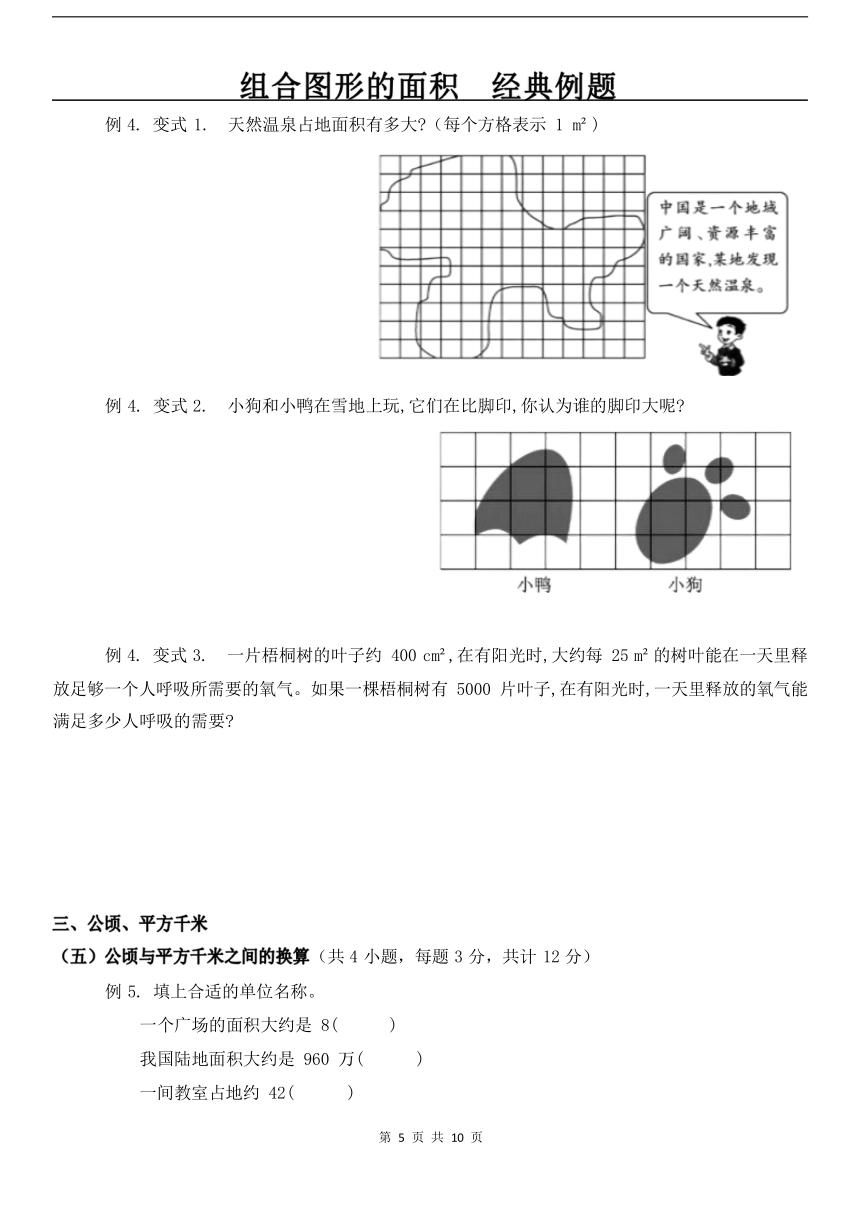
例 4. 变式 1. 天然温泉占地面积有多大 (每个方格表示 1 m )
例 4. 变式 2. 小狗和小鸭在雪地上玩,它们在比脚印,你认为谁的脚印大呢
例 4. 变式 3. 一片梧桐树的叶子约 400 cm ,在有阳光时,大约每 25 m 的树叶能在一天里释 放足够一个人呼吸所需要的氧气。如果一棵梧桐树有 5000 片叶子,在有阳光时,一天里释放的氧气能
满足多少人呼吸的需要
三、公顷、平方千米
(五)公顷与平方千米之间的换算(共 4 小题,每题 3 分,共计 12 分)
例 5. 填上合适的单位名称。
一个广场的面积大约是 8( )
我国陆地面积大约是 960 万( )
一间教室占地约 42( )
第 5 页 共 10 页
组合图形的面积 经典例题
例 5. 变式 1. 算一算,填一填。
62 平方分米= ( )平方厘米
40000 平方米= ( )公顷
1800 平方分米= ( )平方米
9 平方米= ( )平方分米
26 公顷= ( )平方米
72 平方分米= ( )平方厘米
14 m = ( )dm = ( )cm
例 5. 变式 2. 在○里填上“> ”“< ”或“= ”。
8 公顷○8000 平方米 20 公顷○1 平方千米
5 平方千米○5000000 平方米 60000 平方米○5 公顷
例 5. 变式 3. 选择正确答案填在( )里。
(1)一块正方形手帕,边长是 30 厘米,它的面积是( )。
A.120 平方厘米 B.12 平方厘米 C.9 平方分米 D.9 平方米
(2)把 1 个边长是 1 米的正方形,平均切成 100 个小正方形,每个小正方形边长是( )。
A.1 米 B.1 分米 C.1 厘米
(六)公顷与平方千米之间的换算(共 4 小题,每题 3 分,共计 12 分)
例 6. 判断题。 (对的在括号里打“ √ ”,错的打“ × ”)
(1)周长是 4 分米的正方形,面积是 1 平方分米。 ( )
(2)长度单位的进率是 10,面积单位的进率是 1000。 ( )
(3)8 平方千米+4 平方米=12 平方千米。 ( )
(4)长 50 厘米、宽 40 厘米的长方形,面积是 20 平方分米。 ( )
例 6. 变式 1. 学校长方形操场长 200 米,宽 50 米,操场的面积是多少平方米 合多少公顷
例 6. 变式 2. 有一块长方形的玉米地,长是 12 米,宽是 8 米,这块玉米地的面积是多少平
方米 在这块玉米地的四周围上篱笆,篱笆长多少米
第 6 页 共 10 页
组合图形的面积 经典例题
例 6. 变式 3. 一个果园的长是 200 米,宽是 150 米,每公顷有 20 棵果树,这个果园一共有
多少棵果树
(七)公顷与平方千米之间的换算(共 4 小题,每题 3 分,共计 12 分)
例 7. 一块正方形的果园,周长是 2400 米,面积是多少公顷
例 7. 变式 1. 一个长方形开发区,长 6000 米,比宽多 1000 米,这个开发区的面积是多少平方
千米
例 7. 变式 2. 一台播种机宽 4 米,工作时,以每小时 4.5 千米的速度前进,3 小时可以播种多少
公顷
例 7. 变式 3. 市政府开展“开荒造林 ”活动,打算在一块长 18 千米,宽 6 千米的长方形荒
地上种树,按平均每公顷种树 3500 棵计算,能种多少棵树
第 7 页 共 10 页
组合图形的面积 经典例题
(八)综合运用(共 4 小题,每题 3 分,共计 12 分)
例 8. 填空。
(1)一个梯形,它的下底是 8 厘米,如果将它的上底增加 3 厘米,正好变成一个平行四边形,
这时面积增加 15 平方厘米,原来梯形的面积是( )平方厘米。
(2)如图,平行四边形的底是 10 厘米,高是 6 厘米,阴影部分的面积和是( )平方厘米。
例 8. 变式 1. 填一填。
(
5
公
顷
=
(
)m
1000
公
顷
=
(
)km
2
m =
(
)
cm
) (
200
dm
=
(
)m
1400
cm
=
(
)dm
)1 dm = ( ) cm
12 km = ( ) 公 顷
1 km = ( )m = ( )公顷
(
“<
”“=
”。
)例 8. 变式 2. 在○里填上“> ”
5 公顷○5 平方千米
9 平方米○90 平方分米
400 公顷○4000 平方米
800 平方厘米○8 平方分米
588 平方分米○6 平方米
1 平方千米○100000 平方米
例 8. 变式 3. 求下面组合图形的面积。 (单位:cm)
第 8 页 共 10 页
组合图形的面积 经典例题
(九)综合运用(共 4 小题,每题 3 分,共计 12 分)
例 9. 选择题。
(1)我们学校的占地面积是 9500( )。
A.km B. 公顷 C.m
(2)进率是 100 的两个面积单位是( )。
A. 公顷和 m B.m 和 dm C.m 和 km
(3)梯形的面积是 96 平方厘米,高是 8 厘米,则上、下底的和是( )厘米。
A.12 B.24 C.48
例 9. 变式 1. 判断题。
(1)6 公顷=600 平方米。 ( )
(2)一个直角三角形,三边长分别为 6 cm,8 cm,10 cm,则它的面积为 24cm 。 ( )
(3)两个梯形一定能拼成一个平行四边形。 ( )
例 9. 变式 2. 小丽家装修需要 30 块木板,木板的形状如下图。
(1)一块木板的面积是多少
(2)如果每块木板需要 15 元,那么小丽家买木板需要花多少钱
例 9. 变式 3. 如图,这个长方形的长是 9 cm,宽是 8 cm,A 和 B 是宽的中点,求长方形内阴
影部分的面积。
第 9 页 共 10 页
组合图形的面积 经典例题
(十)综合运用(共 4 小题,每题 3 分,共计 12 分)
例 10. 计算下列图形阴影部分的面积。 (单位:cm)
例 10. 变式 1. 一块长方形菜地,长 60 m,宽 40 m,在这块菜地中间有一个三角形水池,水池
的底边长是 16 m,高是 20 m。这块菜地可以耕种的面积有多大?
例 10. 变式 2. 如图中间是一个正方形的花坛,边长 20 m,在花坛周围有一条宽 2 m 的小路,
小路的面积是多少平方米
例 10. 变式 3. 公园里有一块面积为 180 m2 的三角形绿地(如下图),底是 24 m,为了使周围
的空气更清新,市政府决定把绿地扩展,把底延长 8 m,高不变。
(1)请在下面图上画出扩展后的三角形绿地。 (只画示意图)
(2)计算出扩展后的三角形绿地的总面积。
第 10 页 共 10 页
组合图形的面积 经典例题答案
一、组合图形的面积
(一)组合图形的面积计算(共 4 小题,每题 3 分,共计 12 分)
例 1. 求下面图形的面积。 (单位:cm)
32×10÷2+32×20 3×4÷2+(5+10) ×5÷2 10×12-(4+8) ×2÷2
= 160+640 =6+37.5 =120-12
=800(cm ) =43.5(cm ) = 108(cm )
例 1. 变式 1. 先回答问题,再计算图形的面积。 (单位:cm)
(1)
组合图形的面积= ( 长方形 )面积+( 三角形 )面积
36×24+24×21÷2=1116(平方厘米)
(2)
52
阴影部分的面积= ( 梯形 )面积- ( 三角形 )面积
(30+52) ×28÷2-30×28÷2=728(cm )
例 1. 变式 2. 计算下面图形的面积,你能用不同的计算方法吗
第 1 页 共 10 页
组合图形的面积 经典例题答案
5×2.5+(3+5) ×(5-2.5) ÷2
=5×2.5+8×2.5÷2
= 12.5+10
=22.5(平方米)
5×3+(2.5+5) ×(5-3) ÷2
=5×3+7.5×2÷2
= 15+7.5
=22.5(平方米)
例 1. 变式 3. 如图,左边阴影部分的面积是 60 平方厘米。求右边空白部分(梯形)的面积。 (单
位:厘米)
60×2÷8=15(厘米)
(16+16+8) ×15÷2
=40×15÷2
=300(平方厘米)
答:空白部分的面积是 300 平方厘米.
(二)组合图形的面积计算(共 4 小题,每题 3 分,共计 12 分)
例 2. 计算下列组合图形的面积。 (单位:cm)
(8.5+15) ×13÷2-8.5×4÷2=135.75(cm )
例 2. 变式 1. 解决问题。
下图是一间房子侧面的墙,它的面积是多少 如果每平方米用 120 块砖,砌这面墙一共需要多少
块砖
6×5+(4+6) ×3÷2
=30+15
=45(m )
45×120 =5400(块)
答:砌这面墙一共需要 5400 块.
第 2 页 共 10 页
组合图形的面积 经典例题答案
例 2. 变式 2. 下图是一块地的平面图,求它的面积。 (单位:米)
(30+50) ×25÷2-30×10÷2=850(m )
例 2. 变式 3. 求下图中的阴影部分的面积。 (单位:cm)
2×(6+2) ÷2
=2×8÷2
= 16÷2
=8(cm )
二、成长的脚印
(三)估计不规则图形的面积(共 4 小题,每题 3 分,共计 12 分)
例 3. 想一想,填一填。
估计不规则图形的面积的方法是根据图形的形状,确定一个近似的( 规则图形 ),通过对( 规则
图形 )的计算,估计出不规则图形的面积。
例 3. 变式 1. 估算运动场地在图上的面积。 (小方格的边长为 1 cm)
面积约为: 74 cm 。
例 3. 变式 2. 某公司想购买土地(如图所示)。比一比,在同等价格下购买哪一块划算些 (每
个方格 1 km )
组合图形的面积 经典例题答案
在同等价格下购买第一块土地合适.
例 3. 变式 3. 如图,这是教室的一面墙壁,学校要涂上白色涂料(黑板和墙裙除外)。如果每平
方米需要花费 3.5 元,那么粉刷这样的 20 面墙壁一共需要多少元 (单位:米)
6×5-4×1.5-6×1 3.5×(18×20)
=30-6-6 =3.5×360
=24-6 =1260(元)
= 18(平方米) 答:粉刷这样的 20 面墙壁一共需要 1260 元.
(四)估计不规则图形的面积(共 4 小题,每题 3 分,共计 12 分)
例 4. 一条白色的正方形手帕,它的边长是 18 cm ,手帕上横竖各有两道灰条(如下图所示阴影
部分),灰条宽是 2 cm。这条手帕白色部分的面积是多少
(18-2×2) ×(18-2×2)
=(18-4) ×(18-4)
= 14×14
= 196(平方厘米)
答:这条手帕白色部分的面积是 196 平方厘米.
第 4 页 共 10 页
组合图形的面积 经典例题答案
例 4. 变式 1. 天然温泉占地面积有多大 (每个方格表示 1 m )
解答:
由图意可知,温泉是由大约 70 个小方格组成的,所以温泉的面积是:
70×1 =70(m )
答:温泉的面积是 70m .
例 4. 变式 2. 小狗和小鸭在雪地上玩,它们在比脚印,你认为谁的脚印大呢
我认为小狗的脚印大.
解析:本题考察的是组合图形的面积,可以用数格子的办法解决。
小鸭的脚印大概 6 个多一点点,小狗的脚印大约 7 个方格左右,6<7,所以
我认为小狗的脚大。
注:在数格子时,不满一个格子均按半个格子计算.
例 4. 变式 3. 一片梧桐树的叶子约 400 cm ,在有阳光时,大约每 25 m 的树叶能在一天里释 放足够一个人呼吸所需要的氧气。如果一棵梧桐树有 5000 片叶子,在有阳光时,一天里释放的氧气能
满足多少人呼吸的需要
400×5000=2000000(平方厘米)
2000000 平方厘米=200 平方米
200÷25=8(人)
答:一天里释放的氧气能满足 8 人呼吸的需要.
第 5 页 共 10 页
组合图形的面积 经典例题答案
三、公顷、平方千米
(五)公顷与平方千米之间的换算(共 4 小题,每题 3 分,共计 12 分)
例 5. 填上合适的单位名称。
一个广场的面积大约是 8( 公顷 )
我国陆地面积大约是 960 万( 平方千米 )
一间教室占地约 42( 平方米 )
例 5. 变式 1. 算一算,填一填。
62 平方分米= ( 6200 )平方厘米 9 平方米= ( 900 )平方分米
40000 平方米= ( 4 )公顷 26 公顷= ( 260000 )平方米
1800 平方分米= ( 18 )平方米 72 平方分米= ( 7200 )平方厘米
14 m = ( 1400 )dm = ( 140000 )cm
例 5. 变式 2. 在○里填上“> ”“< ”或“= ”。
8 公顷 800>0 平方米 20 公顷<1 平方千米
5 平方千米=5000000 平方米 60000 平方米>5 公顷
例 5. 变式 3. 选择正确答案填在( )里。
(1)一块正方形手帕,边长是 30 厘米,它的面积是( C )。
A.120 平方厘米 B.12 平方厘米 C.9 平方分米 D.9 平方米
(2)把 1 个边长是 1 米的正方形,平均切成 100 个小正方形,每个小正方形边长是( B )。
A.1 米 B.1 分米 C.1 厘米
(六)公顷与平方千米之间的换算(共 4 小题,每题 3 分,共计 12 分)
例 6. 判断题。 (对的在括号里打“ √ ”,错的打“ × ”)
(1)周长是 4 分米的正方形,面积是 1 平方分米。
(2)长度单位的进率是 10,面积单位的进率是 1000。
(3)8 平方千米+4 平方米=12 平方千米。
( √
( ×
( ×
)
)
)
(4)长 50 厘米、宽 40 厘米的长方形,面积是 20 平方分米。 ( √ )
例 6. 变式 1. 学校长方形操场长 200 米,宽 50 米,操场的面积是多少平方米 合多少公顷
200×50=10000(平方米)
10000 平方米=1 公顷
答:操场的面积是 10000 平方米,合 1 公顷.
第 6 页 共 10 页
组合图形的面积 经典例题答案
例 6. 变式 2. 有一块长方形的玉米地,长是 12 米,宽是 8 米,这块玉米地的面积是多少平方
米 在这块玉米地的四周围上篱笆,篱笆长多少米
12×8=96(平方米)
(12+8)×2=40(米)
答:这块玉米地的面积是 96 平方米,在这块玉米地的四周围上篱笆,篱笆
长 40 米.
例 6. 变式 3. 一个果园的长是 200 米,宽是 150 米,每公顷有 20 棵果树,这个果园一共有
多少棵果树
200 ×150=30000(平方米)
30000 平方米=3 公顷
3×20=60(棵)
答:这个果园一共有 60 棵果树.
(七)公顷与平方千米之间的换算(共 4 小题,每题 3 分,共计 12 分)
例 7. 一块正方形的果园,周长是 2400 米,面积是多少公顷
2400÷4=600(米)
600×600=360000(平方米)
360000 平方米=36 公顷
答:面积是 36 公顷.
例 7. 变式 1. 一个长方形开发区,长 6000 米,比宽多 1000 米,这个开发区的面积是多少平方
千米
6000-1000=5000(米)
6000×5000=30000000(平方米)
30000000 平方米=30(平方千米)
答:这个开发区的面积是 30 平方千米.
例 7. 变式 2. 一台播种机宽 4 米,工作时,以每小时 4.5 千米的速度前进,3 小时可以播种多少
公顷
4.5 千米=4500 米
4500×3×4=54000 平方米 54000 平方米=5.4 公顷
答:3 小时可以播种 5.4 公顷.
第 7 页 共 10 页
组合图形的面积 经典例题答案
例 7. 变式 3. 市政府开展“开荒造林 ”活动,打算在一块长 18 千米,宽 6 千米的长方形荒
地上种树,按平均每公顷种树 3500 棵计算,能种多少棵树
18 ×6=108(平方千米)
108 平方千米=10800 公顷
10800×3500=37800000(棵)
答:能种 37800000 棵树.
(八)综合运用(共 4 小题,每题 3 分,共计 12 分)
例 8. 填空。
(1)一个梯形,它的下底是 8 厘米,如果将它的上底增加 3 厘米,正好变成一个平行四边形,
这时面积增加 15 平方厘米,原来梯形的面积是( 65 )平方厘米。
(2)如图,平行四边形的底是 10 厘米,高是 6 厘米,阴影部分的面积和是( 30 )平方厘米。
例 8. 变式 1. 填一填。
1 dm = ( 100 ) cm 5 公顷= ( 50000 )m 200 dm = ( 2 )m 12
km = ( 1200 )公顷 1000 公顷= ( 10 )km 1400 cm = ( 14 )dm 1
km = ( 1000000 )m = ( 100 )公顷
例 8. 变式 2. 在○里填上“> ”“< ”
5 公顷 5< 平方千米
9 平方米>90 平方分米
400 公顷>4000 平方米
例 8. 变式 3. 求下面组合图形的面积。 (单位:cm)
(20+24) ×20÷2-20×15÷2=290(cm )
6×9+(6+14) ×7÷2=124(cm )
第 8 页 共 10 页
组合图形的面积 经典例题答案
4.5×11+(4.5+11-4.5) ×(5.5-4.5) × =55(cm )
10×16+(8+16) ×4× =208(cm )
(九)综合运用(共 4 小题,每题 3 分,共计 12 分)
例 9. 选择题。
(1)我们学校的占地面积是 9500( C )。
A.km B. 公顷 C.m
(2)进率是 100 的两个面积单位是( B )。
A. 公顷和 m B.m 和 dm C.m 和 km
(3)梯形的面积是 96 平方厘米,高是 8 厘米,则上、下底的和是( B )厘米。
A.12 B.24 C.48
例 9. 变式 1. 判断题。
(1)6 公顷=600 平方米。 ( × )
(2)一个直角三角形,三边长分别为 6 cm,8 cm,10 cm,则它的面积为 24cm 。 ( √ )
(3)两个梯形一定能拼成一个平行四边形。 ( × )
例 9. 变式 2. 小丽家装修需要 30 块木板,木板的形状如下图。
(1)一块木板的面积是多少
48×60+ ×(60-30) ×(72-48)=3240(cm )
(2)如果每块木板需要 15 元,那么小丽家买木板需要花多少钱
30×15=450(元)
例 9. 变式 3. 如图,这个长方形的长是 9 cm,宽是 8 cm,A 和 B 是宽的中点,求长方形内阴
影部分的面积。
8×9÷2÷2 =18(平方厘米)
答:长方形内阴影部分的面积是 18 平方厘米.
组合图形的面积 经典例题答案
(十)综合运用(共 4 小题,每题 3 分,共计 12 分)
例 10. 计算下列图形阴影部分的面积。 (单位:cm)
(6+11) ×12× -5×12× =72(cm ) 22×22+44×17× =858(cm )
例 10. 变式 1.
的底边长是 16 m,高是
一块长方形菜地,长 60 m,宽 40 m,在这块菜地中间有一个三角形水池,水池
20 m。这块菜地可以耕种的面积有多大?
60×40-16×20×
答:这块菜地可以耕种的面积是 2240 平方米.
例 10. 变式 2. 如图中间是一个正方形的花坛,边长 20 m,在花坛周围有一条宽 2 m 的小路,
小路的面积是多少平方米
20+2×2 =24(米)
24×24-20×20
=576-400
= 176(平方米)
答:这条小路的面积是 176 平方米.
例 10. 变式 3. 公园里有一块面积为
180 m 的三角形绿地(如下图),底是 24 m,为了使周围
的空气更清新,市政府决定把绿地扩展,把底延长 8 m,高不变。
(1)请在下面图上画出扩展后的三角形绿地。 (只画示意图)
(2)计算出扩展后的三角形绿地的总面积。
180×2÷24=15(m)
(24+8) ×15÷2=240(m )
答:扩展后的三角形绿地的总面积是 240 平方米.
第 10 页 共 10 页
班级 小组 姓名 成绩 (满分 120)
一、组合图形的面积
(一)组合图形的面积计算(共 4 小题,每题 3 分,共计 12 分)
例 1. 求下面图形的面积。 (单位:cm)
例 1. 变式 1. 先回答问题,再计算图形的面积。 (单位:cm)
(1)
组合图形的面积= ( )面积+( )面积
(2)
52
阴影部分的面积= ( )面积- ( )面积
例 1. 变式 2. 计算下面图形的面积,你能用不同的计算方法吗
第 1 页 共 10 页
组合图形的面积 经典例题
例 1. 变式 3. 如图,左边阴影部分的面积是 60 平方厘米。求右边空白部分(梯形)的面积。(单
位:厘米)
(二)组合图形的面积计算(共 4 小题,每题 3 分,共计 12 分)
例 2. 计算下列组合图形的面积。 (单位:cm)
例 2. 变式 1. 解决问题。
下图是一间房子侧面的墙,它的面积是多少 如果每平方米用 120 块砖,砌这面墙一共需要多
少块砖
第 2 页 共 10 页
组合图形的面积 经典例题
例 2. 变式 2. 下图是一块地的平面图,求它的面积。 (单位:米)
例 2. 变式 3. 求下图中的阴影部分的面积。 (单位:cm)
二、成长的脚印
(三)估计不规则图形的面积(共 4 小题,每题 3 分,共计 12 分)
例 3. 想一想,填一填。
估计不规则图形的面积的方法是根据图形的形状,确定一个近似的( ),通过对( )的
计算,估计出不规则图形的面积。
例 3. 变式 1. 估算运动场地在图上的面积。 (小方格的边长为 1 cm)
面积约为: cm 。
第 3 页 共 10 页
组合图形的面积 经典例题
例 3. 变式 2. 某公司想购买土地(如图所示)。比一比,在同等价格下购买哪一块划算些
(每个方格 1 km )
例 3. 变式 3. 如图,这是教室的一面墙壁,学校要涂上白色涂料(黑板和墙裙除外)。如果每平
方米需要花费 3.5 元,那么粉刷这样的 20 面墙壁一共需要多少元 (单位:米)
(四)估计不规则图形的面积(共 4 小题,每题 3 分,共计 12 分)
例 4. 一条白色的正方形手帕,它的边长是 18 cm ,手帕上横竖各有两道灰条(如下图所示阴影
部分),灰条宽是 2 cm。这条手帕白色部分的面积是多少
第 4 页 共 10 页
组合图形的面积 经典例题
例 4. 变式 1. 天然温泉占地面积有多大 (每个方格表示 1 m )
例 4. 变式 2. 小狗和小鸭在雪地上玩,它们在比脚印,你认为谁的脚印大呢
例 4. 变式 3. 一片梧桐树的叶子约 400 cm ,在有阳光时,大约每 25 m 的树叶能在一天里释 放足够一个人呼吸所需要的氧气。如果一棵梧桐树有 5000 片叶子,在有阳光时,一天里释放的氧气能
满足多少人呼吸的需要
三、公顷、平方千米
(五)公顷与平方千米之间的换算(共 4 小题,每题 3 分,共计 12 分)
例 5. 填上合适的单位名称。
一个广场的面积大约是 8( )
我国陆地面积大约是 960 万( )
一间教室占地约 42( )
第 5 页 共 10 页
组合图形的面积 经典例题
例 5. 变式 1. 算一算,填一填。
62 平方分米= ( )平方厘米
40000 平方米= ( )公顷
1800 平方分米= ( )平方米
9 平方米= ( )平方分米
26 公顷= ( )平方米
72 平方分米= ( )平方厘米
14 m = ( )dm = ( )cm
例 5. 变式 2. 在○里填上“> ”“< ”或“= ”。
8 公顷○8000 平方米 20 公顷○1 平方千米
5 平方千米○5000000 平方米 60000 平方米○5 公顷
例 5. 变式 3. 选择正确答案填在( )里。
(1)一块正方形手帕,边长是 30 厘米,它的面积是( )。
A.120 平方厘米 B.12 平方厘米 C.9 平方分米 D.9 平方米
(2)把 1 个边长是 1 米的正方形,平均切成 100 个小正方形,每个小正方形边长是( )。
A.1 米 B.1 分米 C.1 厘米
(六)公顷与平方千米之间的换算(共 4 小题,每题 3 分,共计 12 分)
例 6. 判断题。 (对的在括号里打“ √ ”,错的打“ × ”)
(1)周长是 4 分米的正方形,面积是 1 平方分米。 ( )
(2)长度单位的进率是 10,面积单位的进率是 1000。 ( )
(3)8 平方千米+4 平方米=12 平方千米。 ( )
(4)长 50 厘米、宽 40 厘米的长方形,面积是 20 平方分米。 ( )
例 6. 变式 1. 学校长方形操场长 200 米,宽 50 米,操场的面积是多少平方米 合多少公顷
例 6. 变式 2. 有一块长方形的玉米地,长是 12 米,宽是 8 米,这块玉米地的面积是多少平
方米 在这块玉米地的四周围上篱笆,篱笆长多少米
第 6 页 共 10 页
组合图形的面积 经典例题
例 6. 变式 3. 一个果园的长是 200 米,宽是 150 米,每公顷有 20 棵果树,这个果园一共有
多少棵果树
(七)公顷与平方千米之间的换算(共 4 小题,每题 3 分,共计 12 分)
例 7. 一块正方形的果园,周长是 2400 米,面积是多少公顷
例 7. 变式 1. 一个长方形开发区,长 6000 米,比宽多 1000 米,这个开发区的面积是多少平方
千米
例 7. 变式 2. 一台播种机宽 4 米,工作时,以每小时 4.5 千米的速度前进,3 小时可以播种多少
公顷
例 7. 变式 3. 市政府开展“开荒造林 ”活动,打算在一块长 18 千米,宽 6 千米的长方形荒
地上种树,按平均每公顷种树 3500 棵计算,能种多少棵树
第 7 页 共 10 页
组合图形的面积 经典例题
(八)综合运用(共 4 小题,每题 3 分,共计 12 分)
例 8. 填空。
(1)一个梯形,它的下底是 8 厘米,如果将它的上底增加 3 厘米,正好变成一个平行四边形,
这时面积增加 15 平方厘米,原来梯形的面积是( )平方厘米。
(2)如图,平行四边形的底是 10 厘米,高是 6 厘米,阴影部分的面积和是( )平方厘米。
例 8. 变式 1. 填一填。
(
5
公
顷
=
(
)m
1000
公
顷
=
(
)km
2
m =
(
)
cm
) (
200
dm
=
(
)m
1400
cm
=
(
)dm
)1 dm = ( ) cm
12 km = ( ) 公 顷
1 km = ( )m = ( )公顷
(
“<
”“=
”。
)例 8. 变式 2. 在○里填上“> ”
5 公顷○5 平方千米
9 平方米○90 平方分米
400 公顷○4000 平方米
800 平方厘米○8 平方分米
588 平方分米○6 平方米
1 平方千米○100000 平方米
例 8. 变式 3. 求下面组合图形的面积。 (单位:cm)
第 8 页 共 10 页
组合图形的面积 经典例题
(九)综合运用(共 4 小题,每题 3 分,共计 12 分)
例 9. 选择题。
(1)我们学校的占地面积是 9500( )。
A.km B. 公顷 C.m
(2)进率是 100 的两个面积单位是( )。
A. 公顷和 m B.m 和 dm C.m 和 km
(3)梯形的面积是 96 平方厘米,高是 8 厘米,则上、下底的和是( )厘米。
A.12 B.24 C.48
例 9. 变式 1. 判断题。
(1)6 公顷=600 平方米。 ( )
(2)一个直角三角形,三边长分别为 6 cm,8 cm,10 cm,则它的面积为 24cm 。 ( )
(3)两个梯形一定能拼成一个平行四边形。 ( )
例 9. 变式 2. 小丽家装修需要 30 块木板,木板的形状如下图。
(1)一块木板的面积是多少
(2)如果每块木板需要 15 元,那么小丽家买木板需要花多少钱
例 9. 变式 3. 如图,这个长方形的长是 9 cm,宽是 8 cm,A 和 B 是宽的中点,求长方形内阴
影部分的面积。
第 9 页 共 10 页
组合图形的面积 经典例题
(十)综合运用(共 4 小题,每题 3 分,共计 12 分)
例 10. 计算下列图形阴影部分的面积。 (单位:cm)
例 10. 变式 1. 一块长方形菜地,长 60 m,宽 40 m,在这块菜地中间有一个三角形水池,水池
的底边长是 16 m,高是 20 m。这块菜地可以耕种的面积有多大?
例 10. 变式 2. 如图中间是一个正方形的花坛,边长 20 m,在花坛周围有一条宽 2 m 的小路,
小路的面积是多少平方米
例 10. 变式 3. 公园里有一块面积为 180 m2 的三角形绿地(如下图),底是 24 m,为了使周围
的空气更清新,市政府决定把绿地扩展,把底延长 8 m,高不变。
(1)请在下面图上画出扩展后的三角形绿地。 (只画示意图)
(2)计算出扩展后的三角形绿地的总面积。
第 10 页 共 10 页
组合图形的面积 经典例题答案
一、组合图形的面积
(一)组合图形的面积计算(共 4 小题,每题 3 分,共计 12 分)
例 1. 求下面图形的面积。 (单位:cm)
32×10÷2+32×20 3×4÷2+(5+10) ×5÷2 10×12-(4+8) ×2÷2
= 160+640 =6+37.5 =120-12
=800(cm ) =43.5(cm ) = 108(cm )
例 1. 变式 1. 先回答问题,再计算图形的面积。 (单位:cm)
(1)
组合图形的面积= ( 长方形 )面积+( 三角形 )面积
36×24+24×21÷2=1116(平方厘米)
(2)
52
阴影部分的面积= ( 梯形 )面积- ( 三角形 )面积
(30+52) ×28÷2-30×28÷2=728(cm )
例 1. 变式 2. 计算下面图形的面积,你能用不同的计算方法吗
第 1 页 共 10 页
组合图形的面积 经典例题答案
5×2.5+(3+5) ×(5-2.5) ÷2
=5×2.5+8×2.5÷2
= 12.5+10
=22.5(平方米)
5×3+(2.5+5) ×(5-3) ÷2
=5×3+7.5×2÷2
= 15+7.5
=22.5(平方米)
例 1. 变式 3. 如图,左边阴影部分的面积是 60 平方厘米。求右边空白部分(梯形)的面积。 (单
位:厘米)
60×2÷8=15(厘米)
(16+16+8) ×15÷2
=40×15÷2
=300(平方厘米)
答:空白部分的面积是 300 平方厘米.
(二)组合图形的面积计算(共 4 小题,每题 3 分,共计 12 分)
例 2. 计算下列组合图形的面积。 (单位:cm)
(8.5+15) ×13÷2-8.5×4÷2=135.75(cm )
例 2. 变式 1. 解决问题。
下图是一间房子侧面的墙,它的面积是多少 如果每平方米用 120 块砖,砌这面墙一共需要多少
块砖
6×5+(4+6) ×3÷2
=30+15
=45(m )
45×120 =5400(块)
答:砌这面墙一共需要 5400 块.
第 2 页 共 10 页
组合图形的面积 经典例题答案
例 2. 变式 2. 下图是一块地的平面图,求它的面积。 (单位:米)
(30+50) ×25÷2-30×10÷2=850(m )
例 2. 变式 3. 求下图中的阴影部分的面积。 (单位:cm)
2×(6+2) ÷2
=2×8÷2
= 16÷2
=8(cm )
二、成长的脚印
(三)估计不规则图形的面积(共 4 小题,每题 3 分,共计 12 分)
例 3. 想一想,填一填。
估计不规则图形的面积的方法是根据图形的形状,确定一个近似的( 规则图形 ),通过对( 规则
图形 )的计算,估计出不规则图形的面积。
例 3. 变式 1. 估算运动场地在图上的面积。 (小方格的边长为 1 cm)
面积约为: 74 cm 。
例 3. 变式 2. 某公司想购买土地(如图所示)。比一比,在同等价格下购买哪一块划算些 (每
个方格 1 km )
组合图形的面积 经典例题答案
在同等价格下购买第一块土地合适.
例 3. 变式 3. 如图,这是教室的一面墙壁,学校要涂上白色涂料(黑板和墙裙除外)。如果每平
方米需要花费 3.5 元,那么粉刷这样的 20 面墙壁一共需要多少元 (单位:米)
6×5-4×1.5-6×1 3.5×(18×20)
=30-6-6 =3.5×360
=24-6 =1260(元)
= 18(平方米) 答:粉刷这样的 20 面墙壁一共需要 1260 元.
(四)估计不规则图形的面积(共 4 小题,每题 3 分,共计 12 分)
例 4. 一条白色的正方形手帕,它的边长是 18 cm ,手帕上横竖各有两道灰条(如下图所示阴影
部分),灰条宽是 2 cm。这条手帕白色部分的面积是多少
(18-2×2) ×(18-2×2)
=(18-4) ×(18-4)
= 14×14
= 196(平方厘米)
答:这条手帕白色部分的面积是 196 平方厘米.
第 4 页 共 10 页
组合图形的面积 经典例题答案
例 4. 变式 1. 天然温泉占地面积有多大 (每个方格表示 1 m )
解答:
由图意可知,温泉是由大约 70 个小方格组成的,所以温泉的面积是:
70×1 =70(m )
答:温泉的面积是 70m .
例 4. 变式 2. 小狗和小鸭在雪地上玩,它们在比脚印,你认为谁的脚印大呢
我认为小狗的脚印大.
解析:本题考察的是组合图形的面积,可以用数格子的办法解决。
小鸭的脚印大概 6 个多一点点,小狗的脚印大约 7 个方格左右,6<7,所以
我认为小狗的脚大。
注:在数格子时,不满一个格子均按半个格子计算.
例 4. 变式 3. 一片梧桐树的叶子约 400 cm ,在有阳光时,大约每 25 m 的树叶能在一天里释 放足够一个人呼吸所需要的氧气。如果一棵梧桐树有 5000 片叶子,在有阳光时,一天里释放的氧气能
满足多少人呼吸的需要
400×5000=2000000(平方厘米)
2000000 平方厘米=200 平方米
200÷25=8(人)
答:一天里释放的氧气能满足 8 人呼吸的需要.
第 5 页 共 10 页
组合图形的面积 经典例题答案
三、公顷、平方千米
(五)公顷与平方千米之间的换算(共 4 小题,每题 3 分,共计 12 分)
例 5. 填上合适的单位名称。
一个广场的面积大约是 8( 公顷 )
我国陆地面积大约是 960 万( 平方千米 )
一间教室占地约 42( 平方米 )
例 5. 变式 1. 算一算,填一填。
62 平方分米= ( 6200 )平方厘米 9 平方米= ( 900 )平方分米
40000 平方米= ( 4 )公顷 26 公顷= ( 260000 )平方米
1800 平方分米= ( 18 )平方米 72 平方分米= ( 7200 )平方厘米
14 m = ( 1400 )dm = ( 140000 )cm
例 5. 变式 2. 在○里填上“> ”“< ”或“= ”。
8 公顷 800>0 平方米 20 公顷<1 平方千米
5 平方千米=5000000 平方米 60000 平方米>5 公顷
例 5. 变式 3. 选择正确答案填在( )里。
(1)一块正方形手帕,边长是 30 厘米,它的面积是( C )。
A.120 平方厘米 B.12 平方厘米 C.9 平方分米 D.9 平方米
(2)把 1 个边长是 1 米的正方形,平均切成 100 个小正方形,每个小正方形边长是( B )。
A.1 米 B.1 分米 C.1 厘米
(六)公顷与平方千米之间的换算(共 4 小题,每题 3 分,共计 12 分)
例 6. 判断题。 (对的在括号里打“ √ ”,错的打“ × ”)
(1)周长是 4 分米的正方形,面积是 1 平方分米。
(2)长度单位的进率是 10,面积单位的进率是 1000。
(3)8 平方千米+4 平方米=12 平方千米。
( √
( ×
( ×
)
)
)
(4)长 50 厘米、宽 40 厘米的长方形,面积是 20 平方分米。 ( √ )
例 6. 变式 1. 学校长方形操场长 200 米,宽 50 米,操场的面积是多少平方米 合多少公顷
200×50=10000(平方米)
10000 平方米=1 公顷
答:操场的面积是 10000 平方米,合 1 公顷.
第 6 页 共 10 页
组合图形的面积 经典例题答案
例 6. 变式 2. 有一块长方形的玉米地,长是 12 米,宽是 8 米,这块玉米地的面积是多少平方
米 在这块玉米地的四周围上篱笆,篱笆长多少米
12×8=96(平方米)
(12+8)×2=40(米)
答:这块玉米地的面积是 96 平方米,在这块玉米地的四周围上篱笆,篱笆
长 40 米.
例 6. 变式 3. 一个果园的长是 200 米,宽是 150 米,每公顷有 20 棵果树,这个果园一共有
多少棵果树
200 ×150=30000(平方米)
30000 平方米=3 公顷
3×20=60(棵)
答:这个果园一共有 60 棵果树.
(七)公顷与平方千米之间的换算(共 4 小题,每题 3 分,共计 12 分)
例 7. 一块正方形的果园,周长是 2400 米,面积是多少公顷
2400÷4=600(米)
600×600=360000(平方米)
360000 平方米=36 公顷
答:面积是 36 公顷.
例 7. 变式 1. 一个长方形开发区,长 6000 米,比宽多 1000 米,这个开发区的面积是多少平方
千米
6000-1000=5000(米)
6000×5000=30000000(平方米)
30000000 平方米=30(平方千米)
答:这个开发区的面积是 30 平方千米.
例 7. 变式 2. 一台播种机宽 4 米,工作时,以每小时 4.5 千米的速度前进,3 小时可以播种多少
公顷
4.5 千米=4500 米
4500×3×4=54000 平方米 54000 平方米=5.4 公顷
答:3 小时可以播种 5.4 公顷.
第 7 页 共 10 页
组合图形的面积 经典例题答案
例 7. 变式 3. 市政府开展“开荒造林 ”活动,打算在一块长 18 千米,宽 6 千米的长方形荒
地上种树,按平均每公顷种树 3500 棵计算,能种多少棵树
18 ×6=108(平方千米)
108 平方千米=10800 公顷
10800×3500=37800000(棵)
答:能种 37800000 棵树.
(八)综合运用(共 4 小题,每题 3 分,共计 12 分)
例 8. 填空。
(1)一个梯形,它的下底是 8 厘米,如果将它的上底增加 3 厘米,正好变成一个平行四边形,
这时面积增加 15 平方厘米,原来梯形的面积是( 65 )平方厘米。
(2)如图,平行四边形的底是 10 厘米,高是 6 厘米,阴影部分的面积和是( 30 )平方厘米。
例 8. 变式 1. 填一填。
1 dm = ( 100 ) cm 5 公顷= ( 50000 )m 200 dm = ( 2 )m 12
km = ( 1200 )公顷 1000 公顷= ( 10 )km 1400 cm = ( 14 )dm 1
km = ( 1000000 )m = ( 100 )公顷
例 8. 变式 2. 在○里填上“> ”“< ”
5 公顷 5< 平方千米
9 平方米>90 平方分米
400 公顷>4000 平方米
例 8. 变式 3. 求下面组合图形的面积。 (单位:cm)
(20+24) ×20÷2-20×15÷2=290(cm )
6×9+(6+14) ×7÷2=124(cm )
第 8 页 共 10 页
组合图形的面积 经典例题答案
4.5×11+(4.5+11-4.5) ×(5.5-4.5) × =55(cm )
10×16+(8+16) ×4× =208(cm )
(九)综合运用(共 4 小题,每题 3 分,共计 12 分)
例 9. 选择题。
(1)我们学校的占地面积是 9500( C )。
A.km B. 公顷 C.m
(2)进率是 100 的两个面积单位是( B )。
A. 公顷和 m B.m 和 dm C.m 和 km
(3)梯形的面积是 96 平方厘米,高是 8 厘米,则上、下底的和是( B )厘米。
A.12 B.24 C.48
例 9. 变式 1. 判断题。
(1)6 公顷=600 平方米。 ( × )
(2)一个直角三角形,三边长分别为 6 cm,8 cm,10 cm,则它的面积为 24cm 。 ( √ )
(3)两个梯形一定能拼成一个平行四边形。 ( × )
例 9. 变式 2. 小丽家装修需要 30 块木板,木板的形状如下图。
(1)一块木板的面积是多少
48×60+ ×(60-30) ×(72-48)=3240(cm )
(2)如果每块木板需要 15 元,那么小丽家买木板需要花多少钱
30×15=450(元)
例 9. 变式 3. 如图,这个长方形的长是 9 cm,宽是 8 cm,A 和 B 是宽的中点,求长方形内阴
影部分的面积。
8×9÷2÷2 =18(平方厘米)
答:长方形内阴影部分的面积是 18 平方厘米.
组合图形的面积 经典例题答案
(十)综合运用(共 4 小题,每题 3 分,共计 12 分)
例 10. 计算下列图形阴影部分的面积。 (单位:cm)
(6+11) ×12× -5×12× =72(cm ) 22×22+44×17× =858(cm )
例 10. 变式 1.
的底边长是 16 m,高是
一块长方形菜地,长 60 m,宽 40 m,在这块菜地中间有一个三角形水池,水池
20 m。这块菜地可以耕种的面积有多大?
60×40-16×20×
答:这块菜地可以耕种的面积是 2240 平方米.
例 10. 变式 2. 如图中间是一个正方形的花坛,边长 20 m,在花坛周围有一条宽 2 m 的小路,
小路的面积是多少平方米
20+2×2 =24(米)
24×24-20×20
=576-400
= 176(平方米)
答:这条小路的面积是 176 平方米.
例 10. 变式 3. 公园里有一块面积为
180 m 的三角形绿地(如下图),底是 24 m,为了使周围
的空气更清新,市政府决定把绿地扩展,把底延长 8 m,高不变。
(1)请在下面图上画出扩展后的三角形绿地。 (只画示意图)
(2)计算出扩展后的三角形绿地的总面积。
180×2÷24=15(m)
(24+8) ×15÷2=240(m )
答:扩展后的三角形绿地的总面积是 240 平方米.
第 10 页 共 10 页
