1.1 分式课件 (45张PPT) 2024-2025学年数学湘教版八年级上册
文档属性
| 名称 | 1.1 分式课件 (45张PPT) 2024-2025学年数学湘教版八年级上册 |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-19 20:09:31 | ||
图片预览







文档简介
(共45张PPT)
第1章 分式
1.1 分式
第1课时
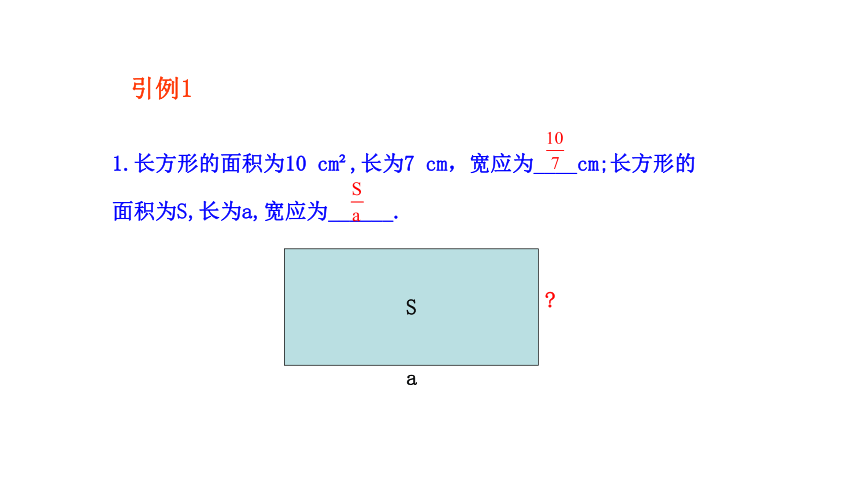
1.长方形的面积为10 cm ,长为7 cm,宽应为____cm;长方形的面积为S,长为a,宽应为______.
S
a
引例1
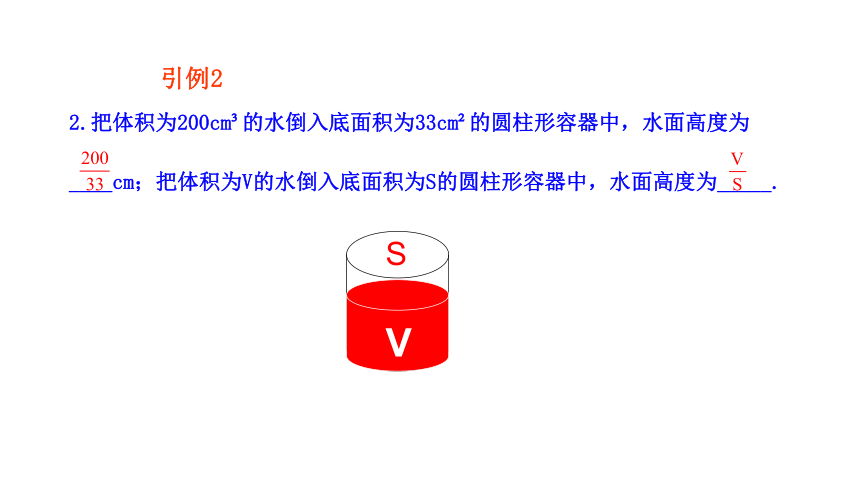
2.把体积为200cm 的水倒入底面积为33cm 的圆柱形容器中,水面高度为____cm;把体积为V的水倒入底面积为S的圆柱形容器中,水面高度为_____.
V
S
引例2
2.能熟练地求出分式的值存在、分式的值不存在及分式值为零的条件.
1.理解分式的概念.
请大家观察式子 和 有什么特点?
请大家观察式子 和 ,有什么特点?
它们与分数有什么相同点和不同点?
都具有分数的形式
相同点
不同点
(观察分母)
分母中有字母
一个整式f除以一个非零整式g(g中含有字母),所得的商记作 , 把代数式 叫作分式,其中f是分式的分子,g是分式的分母,(g≠0).
注意:分式的分子可以含有字母,也可以不含字母,但分式的分母必须含有字母.
概念
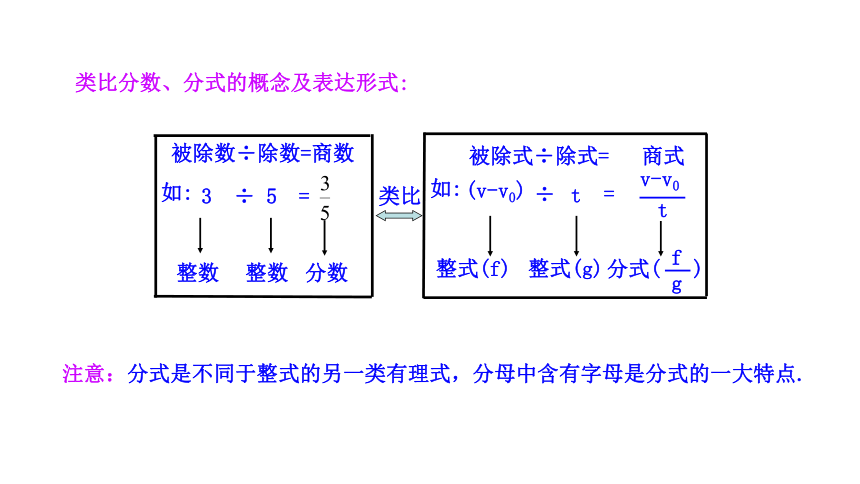
类比分数、分式的概念及表达形式:
整数
整数
分数
整式(f)
整式(g)
分式( )
f
g
注意:分式是不同于整式的另一类有理式,分母中含有字母是分式的一大特点.
t
类比
(v-v0)
÷
t
=
v-v0
3 ÷ 5 =
被除数÷除数=商数
如:
被除式÷除式= 商式
如:
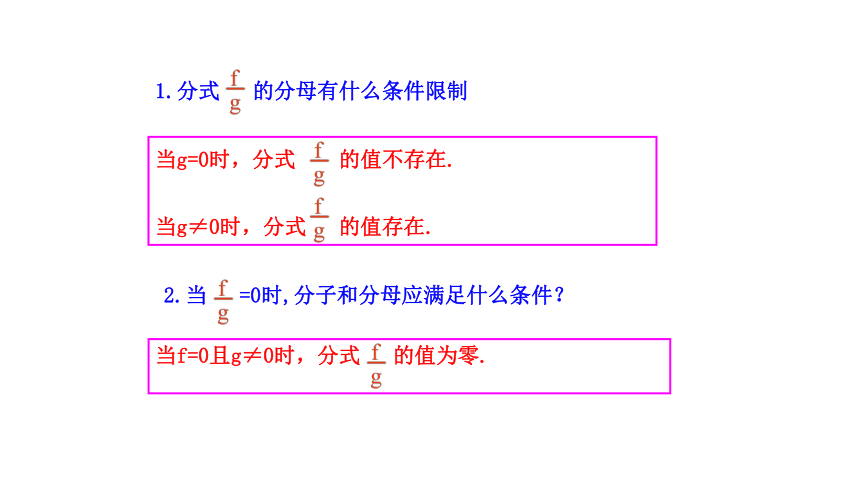
1.分式 的分母有什么条件限制
当g=0时,分式 的值不存在.
当g≠0时,分式 的值存在.
2.当 =0时,分子和分母应满足什么条件?
当f=0且g≠0时,分式 的值为零.
【例题1】
B
【跟踪练习】
C
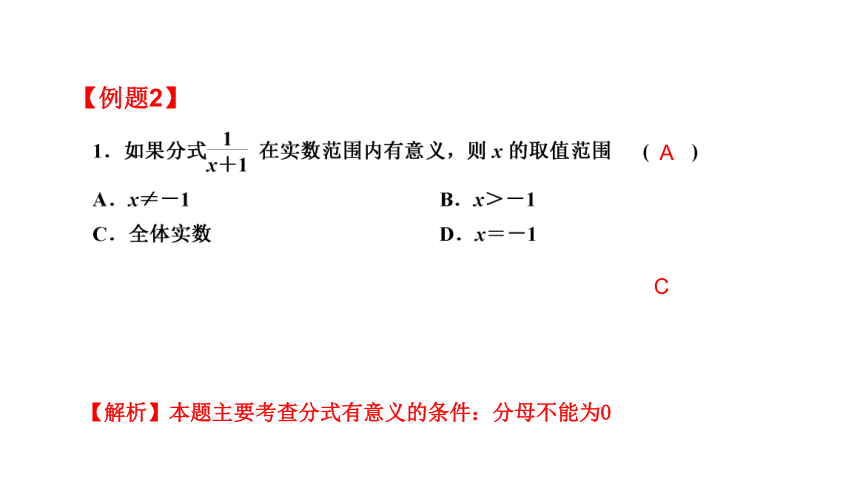
【例题2】
A
C
【解析】本题主要考查分式有意义的条件:分母不能为0
【跟踪练习】
【解析】x+1≠0,分式成立,即x≠-1;
x -1=0,则分式的值等于0,即x=1或-1;
综上,x的值取1。
D
【练习】
B
【例题3】
【跟踪练习】
【跟踪练习】
【跟踪练习】
C
C
D
-6,-4,-3,-1,0,2
解:(1)要使分式有意义,则x2+2x≠0,即x≠0且x≠-2.
(2)要使分式无意义,则x2+2x=0,即x=0或-2.
(3)要使分式的值为0,则|x|-2=0且x2+2x≠0,即x=2.
1.1 分式
第2课时
下列两式成立吗?为什么?
一个分数的分子、分母都乘(或除以)同一个不为零的数,分数的值不变.
分数的基本性质:
即对于任意一个分数 有:
2.能运用分式的基本性质进行简单变形 .
1.理解分式的基本性质 .
相等.
类比分数的基本性质,你能得到分式的基本性质吗?说说看!
如何用语言和式子表示分式的基本性质?
分式的基本性质
其中f,g,h是整式.
分式的分子与分母都乘(或除以)同一个非零整式 ,所得分式与原分式相等.
用语言表示
(2) 成立.因为
所以
例 下列等式成立吗 右边是怎样从左边得到的?
解: (1)成立.因为
所以
【例题1】
xy2
x+y
x+y
x2+2xy+y2
5x
a+b
a+b
a2-b2
【跟踪训练】
C
【例题2】
C
D
【跟踪练习】
这一过程实际上是将分式中分子与分母的公因式约去.
根据分式的基本性质,把一个分式的分子与分母的公因式约去(即分子与分母都除以它们的公因式),叫作分式的约分.
观察下列化简过程,你能发现什么?
那你能不能尝试将下边这个分式进行约分呢?
分子与分母没有公因式的分式叫作最简分式.
(1)若分子﹑分母都是单项式,则约简系数,并约去相同字母的最低次幂;
(2)若分子﹑分母含有多项式,则先将多项式分解因式,然后约去分子﹑分母所有的公因式.
注意:约分过程中,有时还需运用分式的符号法则使最后结果形式简捷;约分的依据是分式的基本性质
约分的基本步骤
【例题1】
C
C
【跟踪练习】
【例题2】
A
【解析】判断分式是否为最简分式,需要找出分式中是否含有公因式.
A.不含有公因式 B.含有公因式x-1
C.含有公因式x-y D.含公因式x+6
D
【解析】判断分式是否为最简分式,需要找出分式中是否含有公因式.
A.含有公因式a
B.含有公因式3
C.含有公因式x+1
D.不含公因式
【跟踪训练】
D
C
C
*
第1章 分式
1.1 分式
第1课时
1.长方形的面积为10 cm ,长为7 cm,宽应为____cm;长方形的面积为S,长为a,宽应为______.
S
a
引例1
2.把体积为200cm 的水倒入底面积为33cm 的圆柱形容器中,水面高度为____cm;把体积为V的水倒入底面积为S的圆柱形容器中,水面高度为_____.
V
S
引例2
2.能熟练地求出分式的值存在、分式的值不存在及分式值为零的条件.
1.理解分式的概念.
请大家观察式子 和 有什么特点?
请大家观察式子 和 ,有什么特点?
它们与分数有什么相同点和不同点?
都具有分数的形式
相同点
不同点
(观察分母)
分母中有字母
一个整式f除以一个非零整式g(g中含有字母),所得的商记作 , 把代数式 叫作分式,其中f是分式的分子,g是分式的分母,(g≠0).
注意:分式的分子可以含有字母,也可以不含字母,但分式的分母必须含有字母.
概念
类比分数、分式的概念及表达形式:
整数
整数
分数
整式(f)
整式(g)
分式( )
f
g
注意:分式是不同于整式的另一类有理式,分母中含有字母是分式的一大特点.
t
类比
(v-v0)
÷
t
=
v-v0
3 ÷ 5 =
被除数÷除数=商数
如:
被除式÷除式= 商式
如:
1.分式 的分母有什么条件限制
当g=0时,分式 的值不存在.
当g≠0时,分式 的值存在.
2.当 =0时,分子和分母应满足什么条件?
当f=0且g≠0时,分式 的值为零.
【例题1】
B
【跟踪练习】
C
【例题2】
A
C
【解析】本题主要考查分式有意义的条件:分母不能为0
【跟踪练习】
【解析】x+1≠0,分式成立,即x≠-1;
x -1=0,则分式的值等于0,即x=1或-1;
综上,x的值取1。
D
【练习】
B
【例题3】
【跟踪练习】
【跟踪练习】
【跟踪练习】
C
C
D
-6,-4,-3,-1,0,2
解:(1)要使分式有意义,则x2+2x≠0,即x≠0且x≠-2.
(2)要使分式无意义,则x2+2x=0,即x=0或-2.
(3)要使分式的值为0,则|x|-2=0且x2+2x≠0,即x=2.
1.1 分式
第2课时
下列两式成立吗?为什么?
一个分数的分子、分母都乘(或除以)同一个不为零的数,分数的值不变.
分数的基本性质:
即对于任意一个分数 有:
2.能运用分式的基本性质进行简单变形 .
1.理解分式的基本性质 .
相等.
类比分数的基本性质,你能得到分式的基本性质吗?说说看!
如何用语言和式子表示分式的基本性质?
分式的基本性质
其中f,g,h是整式.
分式的分子与分母都乘(或除以)同一个非零整式 ,所得分式与原分式相等.
用语言表示
(2) 成立.因为
所以
例 下列等式成立吗 右边是怎样从左边得到的?
解: (1)成立.因为
所以
【例题1】
xy2
x+y
x+y
x2+2xy+y2
5x
a+b
a+b
a2-b2
【跟踪训练】
C
【例题2】
C
D
【跟踪练习】
这一过程实际上是将分式中分子与分母的公因式约去.
根据分式的基本性质,把一个分式的分子与分母的公因式约去(即分子与分母都除以它们的公因式),叫作分式的约分.
观察下列化简过程,你能发现什么?
那你能不能尝试将下边这个分式进行约分呢?
分子与分母没有公因式的分式叫作最简分式.
(1)若分子﹑分母都是单项式,则约简系数,并约去相同字母的最低次幂;
(2)若分子﹑分母含有多项式,则先将多项式分解因式,然后约去分子﹑分母所有的公因式.
注意:约分过程中,有时还需运用分式的符号法则使最后结果形式简捷;约分的依据是分式的基本性质
约分的基本步骤
【例题1】
C
C
【跟踪练习】
【例题2】
A
【解析】判断分式是否为最简分式,需要找出分式中是否含有公因式.
A.不含有公因式 B.含有公因式x-1
C.含有公因式x-y D.含公因式x+6
D
【解析】判断分式是否为最简分式,需要找出分式中是否含有公因式.
A.含有公因式a
B.含有公因式3
C.含有公因式x+1
D.不含公因式
【跟踪训练】
D
C
C
*
同课章节目录
