初中数学湘教版(2024)八年级上册 1.3.1 同底数幂的除法课件(21张PPT)
文档属性
| 名称 | 初中数学湘教版(2024)八年级上册 1.3.1 同底数幂的除法课件(21张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 981.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-19 20:14:05 | ||
图片预览






文档简介
(共21张PPT)
1.3 整数指数幂
1.3.1 同底数幂的除法
an 表示的意义是什么?其中a,n,an分别叫作什么
an
底数
幂
指数
an = a × a × a ×… a
n个a
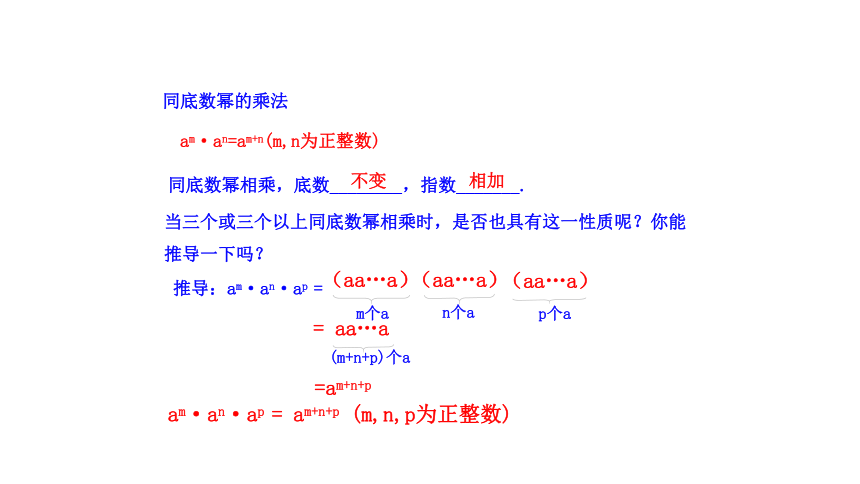
am·an=am+n(m,n为正整数)
同底数幂相乘,底数________,指数_______.
不变
相加
同底数幂的乘法
当三个或三个以上同底数幂相乘时,是否也具有这一性质呢?你能推导一下吗?
推导:am·an·ap =
n个a
= aa…a
=am+n+p
(m+n+p)个a
(aa…a)
(aa…a)
m个a
(aa…a)
p个a
am·an·ap = am+n+p (m,n,p为正整数)
计算下列各式.
(1)b5 ·b;
(3)-a2·a6;
(4)y2n·yn+1.
(2)10×102×103 ;
解:(1)b5·b =b5+1 =b6;
(2)10×102×103 =101+2+3 =106 ;
(3)-a2·a6 =-a2+6 =-a8 ;
(4)y2n·yn+1 =y2n+n+1 =y3n+1.
回顾小练习
1.通过探索,归纳同底数幂的除法法则.
2.熟练进行同底数幂的除法运算.
3.通过同底数幂除法的应用,使学生感受数学应用的价值,提高学习热情.
1.计算:
(1)( )·28=216 (2)( )·53=55
(3)( )·105=107 (4)( )·a3=a6
28
52
102
a3
2.计算:
(1)216÷28=( ) (2)55÷53=( )
(3)107÷105=( ) (4)a6÷a3=( )
28
52
102
a3
上述运算能否发现商与除数、被除数有什么关系?
同底数幂的除法
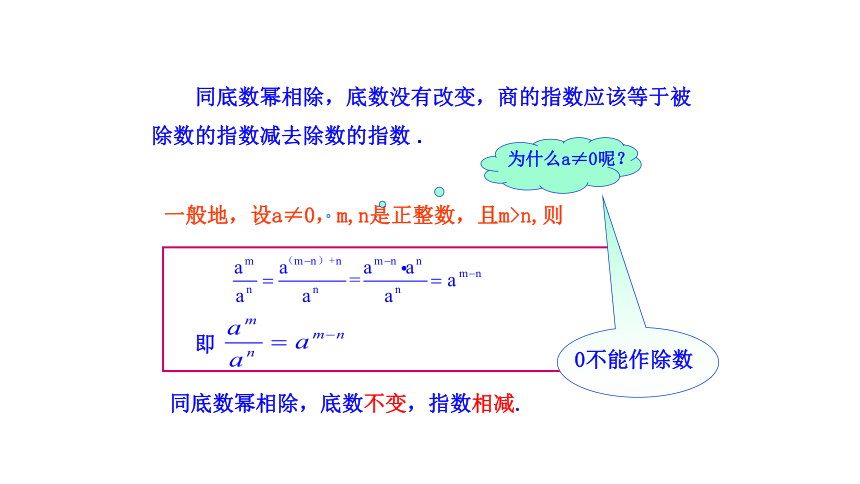
同底数幂相除,底数没有改变,商的指数应该等于被除数的指数减去除数的指数 .
同底数幂相除,底数不变,指数相减.
一般地,设a≠0,m,n是正整数,且m>n,则
为什么a≠0呢?
0不能作除数
即
【例题1】
分析:(1)(2)直接利用同底数幂的除法公式求解;(3)(4)先化为同底数幂相除,再计算.
点评:在(3)中,要把(x-2)看作一个整体,另外要注意(2-x)4=(x-2)4,(2-x)3=-(x-2)3.
【跟踪训练】
【例题2】
【解析】此题考察同底数幂除法的基本概念
a10÷a2(a≠0)的结果是a8
C
计算a10÷a2(a≠0)的结果是 ( )
A.a5 B.a-5
C.a8 D.a-8
【跟踪练习】
某种液体中每升含有1012个有害细菌,某种杀虫剂1滴可杀死109个此种有害细菌.现要将这种2升液体中的有害细菌杀死,要用这种杀虫剂 ( )
A.1000滴 B.2000滴
C.3000滴 D.5000滴
B
【解析】此题考察同底数幂除法的综合运用
2*1012÷109
=2000
【例题3】
C
【跟踪训练】
B
D
(1) a9÷a3
(2) 212÷27
=a9-3=a6
=212-7=25=32
(3)(-x)4÷(-x)
=(-x)4-1=(-x)3=-x3
(4)(-3)11÷(-3)8
=(-3)11-8=(-3)3=-27
1.计算:
3.若10m=16,10n=20,求10m-n的值.
解:因为10m =16,10n=20,
所以10m-n =10m ÷10n =16÷20=0.8
4.已知am=2,an=4,ak=32(a≠0).
(1)求a3m+2n-k的值;
(2)求k-3m-n的值.
解:(1)因为a3m=23,a2n=42=24,ak=32=25,所以a3m+2n-k=a3m·a2n÷ak=23×24÷25=23+4-5=22=4. (2)因为ak-3m-n=25÷23÷22=20=1=a0,所以k-3m-n=0,即k-3m-n的值是0.
5.已知25a×52b=56,4b÷4c=4,求代数式a2+ab+3c值.
解:因为25a×52b=56,4b÷4c=4,所以52a+2b=56,4b-c=4,所以a+b=3,b-c=1.两式相减,可得a+c=2,所以a2+ab+3c=a(a+b)+3c=3a+3c=3(a+c)=3×2=6.
6.已知:xa=4,xb=9,
求(1)xa-b.(2)x3a-2b
这种思维叫作逆向思维!
解:(1)xa-b=xa÷xb=4÷9=
(2)x3a-2b=x3a÷x2b=(xa)3÷(xb)2
=43÷92=
从来没有人读书,只有人在书中读自己,发现自己或检查自己。
——罗曼 罗兰
1.3 整数指数幂
1.3.1 同底数幂的除法
an 表示的意义是什么?其中a,n,an分别叫作什么
an
底数
幂
指数
an = a × a × a ×… a
n个a
am·an=am+n(m,n为正整数)
同底数幂相乘,底数________,指数_______.
不变
相加
同底数幂的乘法
当三个或三个以上同底数幂相乘时,是否也具有这一性质呢?你能推导一下吗?
推导:am·an·ap =
n个a
= aa…a
=am+n+p
(m+n+p)个a
(aa…a)
(aa…a)
m个a
(aa…a)
p个a
am·an·ap = am+n+p (m,n,p为正整数)
计算下列各式.
(1)b5 ·b;
(3)-a2·a6;
(4)y2n·yn+1.
(2)10×102×103 ;
解:(1)b5·b =b5+1 =b6;
(2)10×102×103 =101+2+3 =106 ;
(3)-a2·a6 =-a2+6 =-a8 ;
(4)y2n·yn+1 =y2n+n+1 =y3n+1.
回顾小练习
1.通过探索,归纳同底数幂的除法法则.
2.熟练进行同底数幂的除法运算.
3.通过同底数幂除法的应用,使学生感受数学应用的价值,提高学习热情.
1.计算:
(1)( )·28=216 (2)( )·53=55
(3)( )·105=107 (4)( )·a3=a6
28
52
102
a3
2.计算:
(1)216÷28=( ) (2)55÷53=( )
(3)107÷105=( ) (4)a6÷a3=( )
28
52
102
a3
上述运算能否发现商与除数、被除数有什么关系?
同底数幂的除法
同底数幂相除,底数没有改变,商的指数应该等于被除数的指数减去除数的指数 .
同底数幂相除,底数不变,指数相减.
一般地,设a≠0,m,n是正整数,且m>n,则
为什么a≠0呢?
0不能作除数
即
【例题1】
分析:(1)(2)直接利用同底数幂的除法公式求解;(3)(4)先化为同底数幂相除,再计算.
点评:在(3)中,要把(x-2)看作一个整体,另外要注意(2-x)4=(x-2)4,(2-x)3=-(x-2)3.
【跟踪训练】
【例题2】
【解析】此题考察同底数幂除法的基本概念
a10÷a2(a≠0)的结果是a8
C
计算a10÷a2(a≠0)的结果是 ( )
A.a5 B.a-5
C.a8 D.a-8
【跟踪练习】
某种液体中每升含有1012个有害细菌,某种杀虫剂1滴可杀死109个此种有害细菌.现要将这种2升液体中的有害细菌杀死,要用这种杀虫剂 ( )
A.1000滴 B.2000滴
C.3000滴 D.5000滴
B
【解析】此题考察同底数幂除法的综合运用
2*1012÷109
=2000
【例题3】
C
【跟踪训练】
B
D
(1) a9÷a3
(2) 212÷27
=a9-3=a6
=212-7=25=32
(3)(-x)4÷(-x)
=(-x)4-1=(-x)3=-x3
(4)(-3)11÷(-3)8
=(-3)11-8=(-3)3=-27
1.计算:
3.若10m=16,10n=20,求10m-n的值.
解:因为10m =16,10n=20,
所以10m-n =10m ÷10n =16÷20=0.8
4.已知am=2,an=4,ak=32(a≠0).
(1)求a3m+2n-k的值;
(2)求k-3m-n的值.
解:(1)因为a3m=23,a2n=42=24,ak=32=25,所以a3m+2n-k=a3m·a2n÷ak=23×24÷25=23+4-5=22=4. (2)因为ak-3m-n=25÷23÷22=20=1=a0,所以k-3m-n=0,即k-3m-n的值是0.
5.已知25a×52b=56,4b÷4c=4,求代数式a2+ab+3c值.
解:因为25a×52b=56,4b÷4c=4,所以52a+2b=56,4b-c=4,所以a+b=3,b-c=1.两式相减,可得a+c=2,所以a2+ab+3c=a(a+b)+3c=3a+3c=3(a+c)=3×2=6.
6.已知:xa=4,xb=9,
求(1)xa-b.(2)x3a-2b
这种思维叫作逆向思维!
解:(1)xa-b=xa÷xb=4÷9=
(2)x3a-2b=x3a÷x2b=(xa)3÷(xb)2
=43÷92=
从来没有人读书,只有人在书中读自己,发现自己或检查自己。
——罗曼 罗兰
同课章节目录
