湘教版(2024)数学八年级上册1.3.3 整数指数幂的运算法则 课件(共20张PPT)
文档属性
| 名称 | 湘教版(2024)数学八年级上册1.3.3 整数指数幂的运算法则 课件(共20张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 996.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-19 20:11:31 | ||
图片预览








文档简介
(共20张PPT)
1.3.3 整数指数幂的运算法则
(1) (m,n都是正整数)
(2) (m,n都是正整数)
(3) (n是正整数)
(a≠0,m,n都是正整数,m>n)
(5) (b≠0, n是正整数)
正整数指数幂有以下运算性质:
1.通过探索把正整数指数幂的运算法则推广到整数指数幂的运算法则.
2.会用整数指数幂的运算法则熟练进行计算.
一般地,am中指数m可以是负整数吗?如果可以,那么负整数指数幂am表示什么?
归纳:
am÷an=am-n这条性质对于m,n是任意整数的情形仍然适用.
(a≠0)
【例题1】
计算:
(1)(a-1b3)3;
(2)-a2b-2·(a3b-2)-2.
分析:根据整数指数幂的运算法则计算.
提醒:计算结果中不要含负整数指数幂和零次幂.
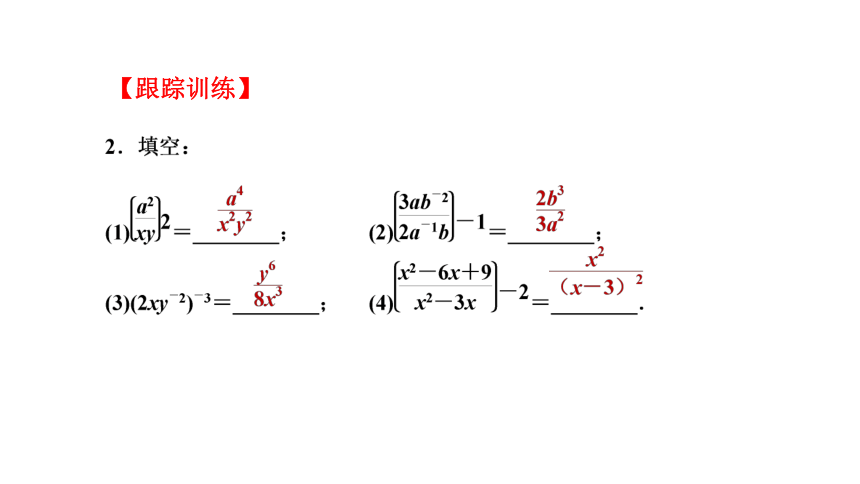
【跟踪训练】
D
【例题2】
分析:先将分式约分、再计算负整数指数幂.
提醒:分式乘方,若分子、分母可以因式分解,则先因式分解,然后约分化简,最后乘方.
【跟踪训练】
【跟踪训练】
27a12b6
a
x3
【例题3】
分析:先将分式约分、再将负整数指数幂转换为倒数形式.
1.计算下列各式,并把结果化为只含有正整数指数幂的形式:
(1)(a-3)2(ab2)-3.
(2)(2mn2)-2(m-2n-1)-3.
(3)(x-3yz-2)2.
【跟踪训练】
【跟踪训练】
.
.
.
.
D
2. 化简(x-1)2·x3的结果是( )
A.x5 B.x4 C.x D.
【解析】(x-1)2·x3=x-2·x3=x-2+3=x.
C
3.下列运算中,正确的个数是( )
①x2+x3=2x5,②(x2)3=x6,③30×2-1=5,④-|-5|+3=8,
A.1个 B.2个 C.3个 D.4个
【解析】因为①错误;③30×2-1=1×2-1=1,
④-|-5|+3=-5+3=-2,所以只有②正确.
A
4.计算:
(1)(ab-2)2·(-2a-1b)3;
(2)(2m2n-3)2·(m2n-1)-3÷(m-1n)2;
解:原式=-2+1-1+3=1.
(4)(4×10-6)2÷(2×10-7).
解:原式=(16×10-12)÷(2×10-7)=8×10-5.
知识是从刻苦劳动中得来的,任何成就都是刻苦劳动的结果。
——宋庆龄
1.3.3 整数指数幂的运算法则
(1) (m,n都是正整数)
(2) (m,n都是正整数)
(3) (n是正整数)
(a≠0,m,n都是正整数,m>n)
(5) (b≠0, n是正整数)
正整数指数幂有以下运算性质:
1.通过探索把正整数指数幂的运算法则推广到整数指数幂的运算法则.
2.会用整数指数幂的运算法则熟练进行计算.
一般地,am中指数m可以是负整数吗?如果可以,那么负整数指数幂am表示什么?
归纳:
am÷an=am-n这条性质对于m,n是任意整数的情形仍然适用.
(a≠0)
【例题1】
计算:
(1)(a-1b3)3;
(2)-a2b-2·(a3b-2)-2.
分析:根据整数指数幂的运算法则计算.
提醒:计算结果中不要含负整数指数幂和零次幂.
【跟踪训练】
D
【例题2】
分析:先将分式约分、再计算负整数指数幂.
提醒:分式乘方,若分子、分母可以因式分解,则先因式分解,然后约分化简,最后乘方.
【跟踪训练】
【跟踪训练】
27a12b6
a
x3
【例题3】
分析:先将分式约分、再将负整数指数幂转换为倒数形式.
1.计算下列各式,并把结果化为只含有正整数指数幂的形式:
(1)(a-3)2(ab2)-3.
(2)(2mn2)-2(m-2n-1)-3.
(3)(x-3yz-2)2.
【跟踪训练】
【跟踪训练】
.
.
.
.
D
2. 化简(x-1)2·x3的结果是( )
A.x5 B.x4 C.x D.
【解析】(x-1)2·x3=x-2·x3=x-2+3=x.
C
3.下列运算中,正确的个数是( )
①x2+x3=2x5,②(x2)3=x6,③30×2-1=5,④-|-5|+3=8,
A.1个 B.2个 C.3个 D.4个
【解析】因为①错误;③30×2-1=1×2-1=1,
④-|-5|+3=-5+3=-2,所以只有②正确.
A
4.计算:
(1)(ab-2)2·(-2a-1b)3;
(2)(2m2n-3)2·(m2n-1)-3÷(m-1n)2;
解:原式=-2+1-1+3=1.
(4)(4×10-6)2÷(2×10-7).
解:原式=(16×10-12)÷(2×10-7)=8×10-5.
知识是从刻苦劳动中得来的,任何成就都是刻苦劳动的结果。
——宋庆龄
同课章节目录
