2.1 三角形 第1课时 课件(共24张PPT)初中数学湘教版八年级上册
文档属性
| 名称 | 2.1 三角形 第1课时 课件(共24张PPT)初中数学湘教版八年级上册 |

|
|
| 格式 | ppt | ||
| 文件大小 | 1018.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-19 20:24:17 | ||
图片预览




文档简介
(共24张PPT)
第2章 三角形
2.1 三角形
第1课时
1.理解三角形的有关概念.
2.掌握三角形的三边关系,并会灵活运用.
A
B
C
不在同一直线上的三条线段首尾相接所构成的图形叫作三角形.
注意:1、不在同一条直线上; 2、首尾相接.
注意:表示三角形时,字母没有先后顺序.即:可以记作△ABC,也可记作△ACB.
2.三角形的表示:
三角形用符号“△”表示,如上图的三角形,记作“△ABC”,读作“三角形ABC”.
1.三角形的定义:
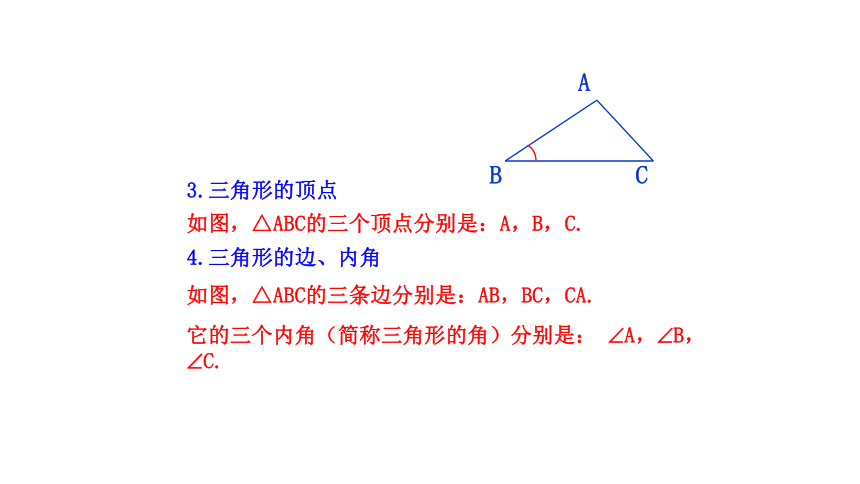
如图,△ABC的三个顶点分别是:A,B,C.
3.三角形的顶点
如图,△ABC的三条边分别是:AB,BC,CA.
它的三个内角(简称三角形的角)分别是: A, B, C.
A
B
C
4.三角形的边、内角
A
B
C
a
b
c
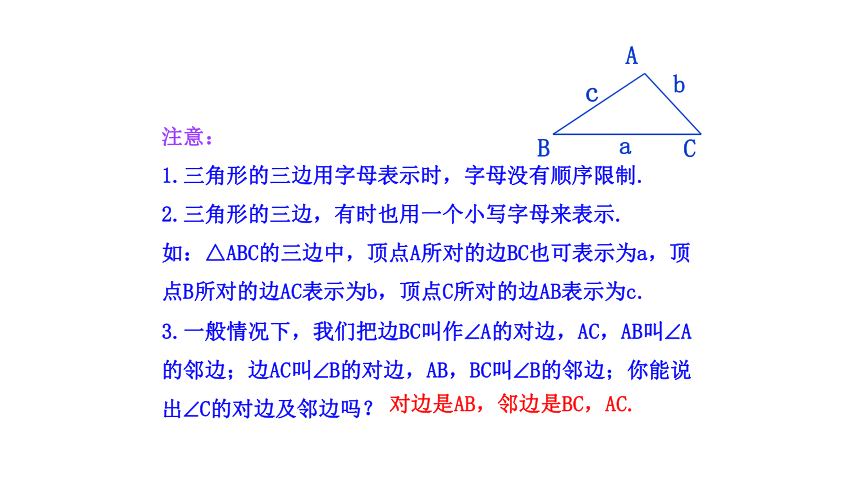
注意:
1.三角形的三边用字母表示时,字母没有顺序限制.
2.三角形的三边,有时也用一个小写字母来表示.
如:△ABC的三边中,顶点A所对的边BC也可表示为a,顶点B所对的边AC表示为b,顶点C所对的边AB表示为c.
3.一般情况下,我们把边BC叫作 A的对边,AC,AB叫 A的邻边;边AC叫 B的对边,AB,BC叫 B的邻边;你能说出 C的对边及邻边吗?
对边是AB,邻边是BC,AC.
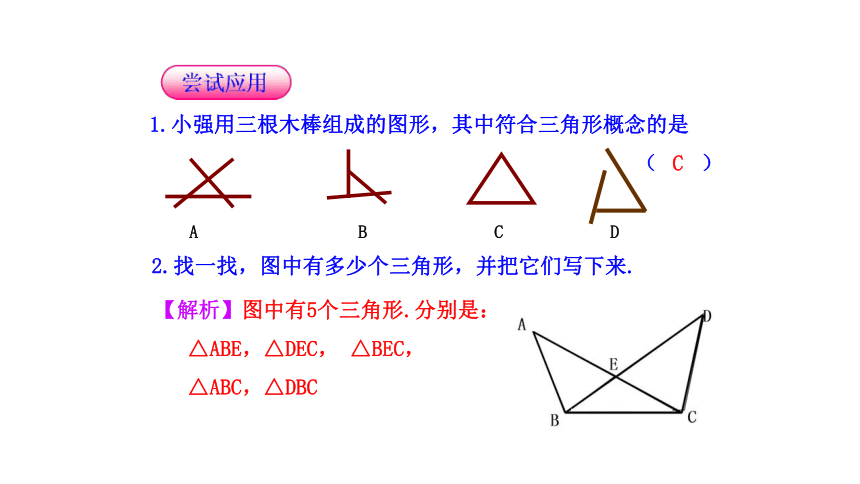
1.小强用三根木棒组成的图形,其中符合三角形概念的是
( )
B
A
C
C
2.找一找,图中有多少个三角形,并把它们写下来.
【解析】图中有5个三角形.分别是:
△ABE,△DEC, △BEC,
△ABC,△DBC
D
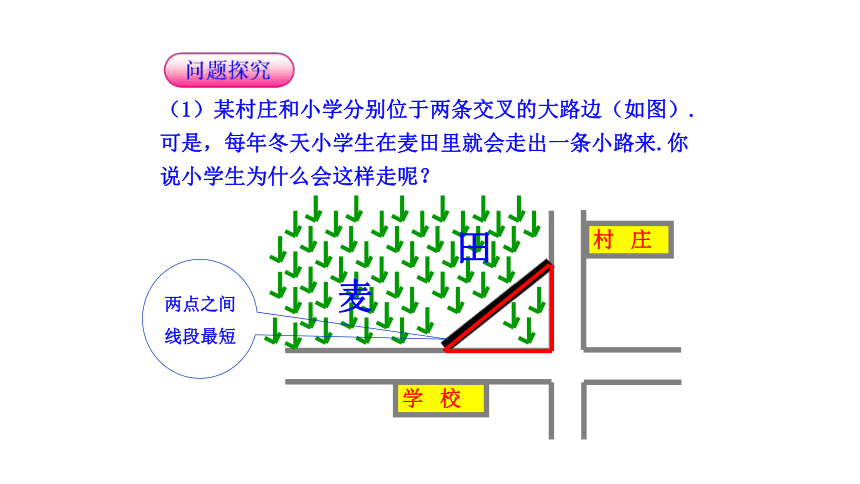
(1)某村庄和小学分别位于两条交叉的大路边(如图).可是,每年冬天小学生在麦田里就会走出一条小路来.你说小学生为什么会这样走呢?
村 庄
学 校
麦
田
两点之间线段最短
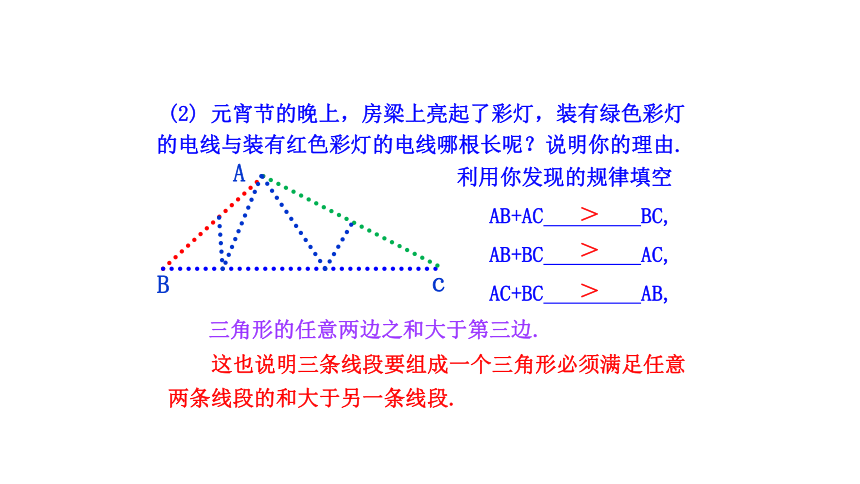
(2) 元宵节的晚上,房梁上亮起了彩灯,装有绿色彩灯的电线与装有红色彩灯的电线哪根长呢?说明你的理由.
利用你发现的规律填空
AB+AC BC,
AB+BC AC,
AC+BC AB,
A
B
c
>
>
>
三角形的任意两边之和大于第三边.
这也说明三条线段要组成一个三角形必须满足任意两条线段的和大于另一条线段.
下列长度的三条线段能否组成三角形?为什么?
(1) 3,4,8 ( )
(2) 2,5,6 ( )
(3) 5,6,10 ( )
(4) 3,5,8 ( )
不能
能
能
不能
判断三条线段能否组成三角形,是否一定要检验三条线段中任何两条的和都大于第三条?有没有更简便的判断方法?
小窍门:用较短的两条线段之和与最长的线段比较,若和大,能组成三角形,反之,则不能.
A
B
C
a
b
c
三角形的任意两边之差小于第三边.
如右图:在ABC中,
a-b<c,
b-c<a,
c-a<b.
在一个三角形中,任意两边之差与第三边有什么关系?
请同学们自己在本子上任意画一个三角形,量出三边的长,再用任意两边的差与第三边比较,得出什么样的结论?
注意:
1.一个三角形的三边关系可以归纳成如下一句话:三角形的任何两边之和大于第三边,任何两边之差小于第三边.
2.在做题时,不仅要考虑到两边之和大于第三边,还必须考虑到两边之差小于第三边.
【例题1】
C
【跟踪训练】
∠ABE
∠ACD
△ABE与△ACE
【例题2】
B
【跟踪训练】
D
【例题3】
C
【跟踪训练】
C
三角形的三边关系
1.【核心素养题】有四根长度分别为3,4,5,x(x为正整数)的木棒,从中任取三根,首尾顺次相接都能组成一个三角形,则组成的三角形的周长 ( )
A.最小值是11 B.最小值是12
C.最大值是14 D.最大值是15
2.一个三角形的两条边长分别是2厘米和9厘米,第三条边的长是一个奇数,则这个三角形的形状是 ( )
A.一般三角形 B.等腰三角形
C.等边三角形 D.无法确定
D
B
3.【江苏徐州中考】下列长度的三条线段,能组成三角形的是 ( )
A.2,2,4 B.5,6,12
C.5,7,2 D.6,8,10
4.下图中三角形的个数为 ( )
A.5 B.8
C.10 D.15
D
C
5.有3 cm,6 cm,8 cm,9 cm的四条线段,任选其中的三条线段组成一个三角形,则最多能组成的三角形的个数为 ( )
A.1 B.2
C.3 D.4
6.如图,用四条线段首尾相接连成一个框架,其中AB=12,BC=14,CD=18,DA=24,则A,B,C,D任意两点之间的最长距离为______.
C
32
7.已知a,b,c为△ABC的三边长,且b,c满足(b-5)2+|c-7|=0,a为方程|a-3|=2的解,判断三角形ABC的形状并求出△ABC的周长.
解:因为(b-5)2+|c-7|=0,所以b-5=0,c-7=0,所以b=5,c=7.又因为|a-3|=2,所以a=5或a=1.当a=1时,a+b=1+5=6<7,所以a=1不符合题意.所以a=5.此时a=b,故△ABC为等腰三角形,其周长为5+5+7=17.
8.已知△ABC的三边长a,b,c均为整数,且a和b满足|a-4|+(b-1)2=0,求△ABC的第三边的长c.
解:因为|a-4|+(b-1)2=0,所以a=4,b=1.又因为a,b,c均为三角形的三边长,所以4-1<c<4+1,所以3<c<5.因为c为整数,所以c=4.即△ABC的第三边的长c=4.
莫找借口失败,只找理由成功.
第2章 三角形
2.1 三角形
第1课时
1.理解三角形的有关概念.
2.掌握三角形的三边关系,并会灵活运用.
A
B
C
不在同一直线上的三条线段首尾相接所构成的图形叫作三角形.
注意:1、不在同一条直线上; 2、首尾相接.
注意:表示三角形时,字母没有先后顺序.即:可以记作△ABC,也可记作△ACB.
2.三角形的表示:
三角形用符号“△”表示,如上图的三角形,记作“△ABC”,读作“三角形ABC”.
1.三角形的定义:
如图,△ABC的三个顶点分别是:A,B,C.
3.三角形的顶点
如图,△ABC的三条边分别是:AB,BC,CA.
它的三个内角(简称三角形的角)分别是: A, B, C.
A
B
C
4.三角形的边、内角
A
B
C
a
b
c
注意:
1.三角形的三边用字母表示时,字母没有顺序限制.
2.三角形的三边,有时也用一个小写字母来表示.
如:△ABC的三边中,顶点A所对的边BC也可表示为a,顶点B所对的边AC表示为b,顶点C所对的边AB表示为c.
3.一般情况下,我们把边BC叫作 A的对边,AC,AB叫 A的邻边;边AC叫 B的对边,AB,BC叫 B的邻边;你能说出 C的对边及邻边吗?
对边是AB,邻边是BC,AC.
1.小强用三根木棒组成的图形,其中符合三角形概念的是
( )
B
A
C
C
2.找一找,图中有多少个三角形,并把它们写下来.
【解析】图中有5个三角形.分别是:
△ABE,△DEC, △BEC,
△ABC,△DBC
D
(1)某村庄和小学分别位于两条交叉的大路边(如图).可是,每年冬天小学生在麦田里就会走出一条小路来.你说小学生为什么会这样走呢?
村 庄
学 校
麦
田
两点之间线段最短
(2) 元宵节的晚上,房梁上亮起了彩灯,装有绿色彩灯的电线与装有红色彩灯的电线哪根长呢?说明你的理由.
利用你发现的规律填空
AB+AC BC,
AB+BC AC,
AC+BC AB,
A
B
c
>
>
>
三角形的任意两边之和大于第三边.
这也说明三条线段要组成一个三角形必须满足任意两条线段的和大于另一条线段.
下列长度的三条线段能否组成三角形?为什么?
(1) 3,4,8 ( )
(2) 2,5,6 ( )
(3) 5,6,10 ( )
(4) 3,5,8 ( )
不能
能
能
不能
判断三条线段能否组成三角形,是否一定要检验三条线段中任何两条的和都大于第三条?有没有更简便的判断方法?
小窍门:用较短的两条线段之和与最长的线段比较,若和大,能组成三角形,反之,则不能.
A
B
C
a
b
c
三角形的任意两边之差小于第三边.
如右图:在ABC中,
a-b<c,
b-c<a,
c-a<b.
在一个三角形中,任意两边之差与第三边有什么关系?
请同学们自己在本子上任意画一个三角形,量出三边的长,再用任意两边的差与第三边比较,得出什么样的结论?
注意:
1.一个三角形的三边关系可以归纳成如下一句话:三角形的任何两边之和大于第三边,任何两边之差小于第三边.
2.在做题时,不仅要考虑到两边之和大于第三边,还必须考虑到两边之差小于第三边.
【例题1】
C
【跟踪训练】
∠ABE
∠ACD
△ABE与△ACE
【例题2】
B
【跟踪训练】
D
【例题3】
C
【跟踪训练】
C
三角形的三边关系
1.【核心素养题】有四根长度分别为3,4,5,x(x为正整数)的木棒,从中任取三根,首尾顺次相接都能组成一个三角形,则组成的三角形的周长 ( )
A.最小值是11 B.最小值是12
C.最大值是14 D.最大值是15
2.一个三角形的两条边长分别是2厘米和9厘米,第三条边的长是一个奇数,则这个三角形的形状是 ( )
A.一般三角形 B.等腰三角形
C.等边三角形 D.无法确定
D
B
3.【江苏徐州中考】下列长度的三条线段,能组成三角形的是 ( )
A.2,2,4 B.5,6,12
C.5,7,2 D.6,8,10
4.下图中三角形的个数为 ( )
A.5 B.8
C.10 D.15
D
C
5.有3 cm,6 cm,8 cm,9 cm的四条线段,任选其中的三条线段组成一个三角形,则最多能组成的三角形的个数为 ( )
A.1 B.2
C.3 D.4
6.如图,用四条线段首尾相接连成一个框架,其中AB=12,BC=14,CD=18,DA=24,则A,B,C,D任意两点之间的最长距离为______.
C
32
7.已知a,b,c为△ABC的三边长,且b,c满足(b-5)2+|c-7|=0,a为方程|a-3|=2的解,判断三角形ABC的形状并求出△ABC的周长.
解:因为(b-5)2+|c-7|=0,所以b-5=0,c-7=0,所以b=5,c=7.又因为|a-3|=2,所以a=5或a=1.当a=1时,a+b=1+5=6<7,所以a=1不符合题意.所以a=5.此时a=b,故△ABC为等腰三角形,其周长为5+5+7=17.
8.已知△ABC的三边长a,b,c均为整数,且a和b满足|a-4|+(b-1)2=0,求△ABC的第三边的长c.
解:因为|a-4|+(b-1)2=0,所以a=4,b=1.又因为a,b,c均为三角形的三边长,所以4-1<c<4+1,所以3<c<5.因为c为整数,所以c=4.即△ABC的第三边的长c=4.
莫找借口失败,只找理由成功.
同课章节目录
