初中数学湘教版八年级上册 2.1 三角形 (第3课时)课件(34张PPT)
文档属性
| 名称 | 初中数学湘教版八年级上册 2.1 三角形 (第3课时)课件(34张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-19 00:00:00 | ||
图片预览









文档简介
(共34张PPT)
2.1 三角形
第3课时
在一个直角三角形里住着三个内角,平时,它们三兄弟非常团结.可是有一天,老二突然不高兴,发起脾气来,它指着老大说:“你凭什么度数最大,我也要和你一样大!”“不行啊!”老大说:“这是不可能的,否则,我们这个家就再也围不起来了……”“为什么?” 老二很纳闷.
同学们,你们知道其中的道理吗?
内角三兄弟之争
三角形的三个内角和是多少
把三个角拼在一起试试看
你有什么办法可以验证呢
从刚才拼角的过程你能想出证明的办法吗
1.了解三角形的内角和的验证及证明过程;
2.熟练利用三角形的内角和及直角三角形两锐角的
关系解决问题;
3.知道添加辅助线是帮助解决数学问题的常用方法.
C
B
A
三角形内角和定理:三角形的内角和等于180°
已知△ABC,求证:∠A+∠B+∠C=180°
证法1:过A作EF∥BC,
所以∠B=∠2,
(两直线平行,内错角相等)
∠C=∠1.
(两直线平行,内错角相等)
又因为∠2+∠1+∠BAC=180°,
所以∠B+∠C+∠BAC=180°.
F
2
1
E
C
B
A
证法2:延长BC到D,过C作CE∥BA,
所以 ∠A=∠1,(两直线平行,内错角相等)
∠B=∠2.(两直线平行,同位角相等)
又因为∠1+∠2+∠ACB=180°,
所以∠A+∠B+∠ACB=180°.
2
1
E
D
C
B
A
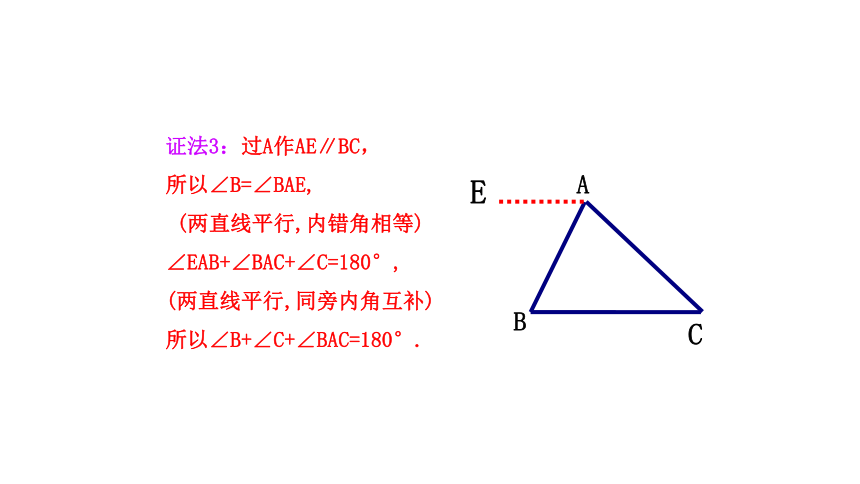
证法3:过A作AE∥BC,
所以∠B=∠BAE,
(两直线平行,内错角相等)
∠EAB+∠BAC+∠C=180°,
(两直线平行,同旁内角互补)
所以∠B+∠C+∠BAC=180°.
C
B
E
A
在这里,为了证明的需要,在原来的图形上添加的线叫作辅助线. 辅助线通常画成虚线.
为了证明三个角的和为180°,转化为一个平角或同旁内角互补,这种转化思想是数学中的常用方法.
【例1】在△ABC中, ∠A :∠B:∠C=2:2:4,求∠A,∠B, ∠C的度数.
解:设每一份角为x°,则∠A=2x°,∠B=2x°, ∠C=4x° ,由三角形内角和定理,可得:
2x+2x+4x=180,
解得 x=22.5,
2x=2×22.5=45, 4x=4×22.5=90.
答: ∠A 为45°,∠B为45°, ∠C为90°.
【例题】
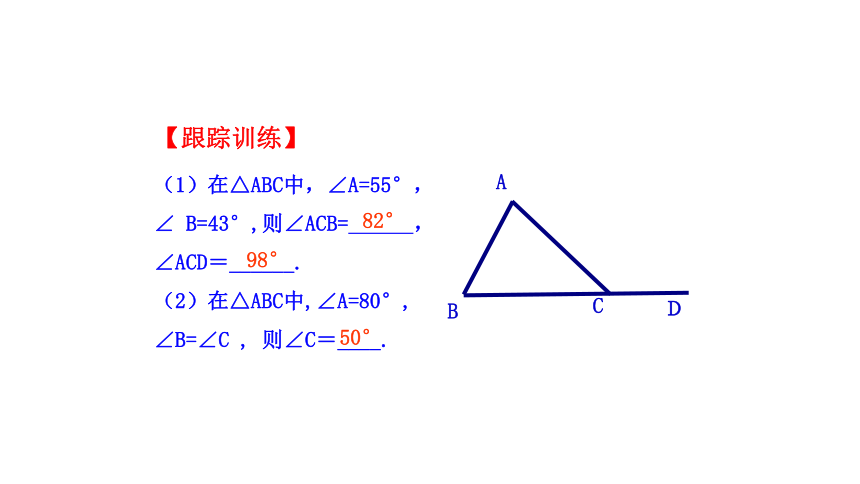
(1)在△ABC中,∠A=55°,
∠ B=43°,则∠ACB= ,
∠ACD=______.
(2)在△ABC中,∠A=80°,
∠B=∠C , 则∠C=____.
82°
C
B
A
D
98°
50°
【跟踪训练】
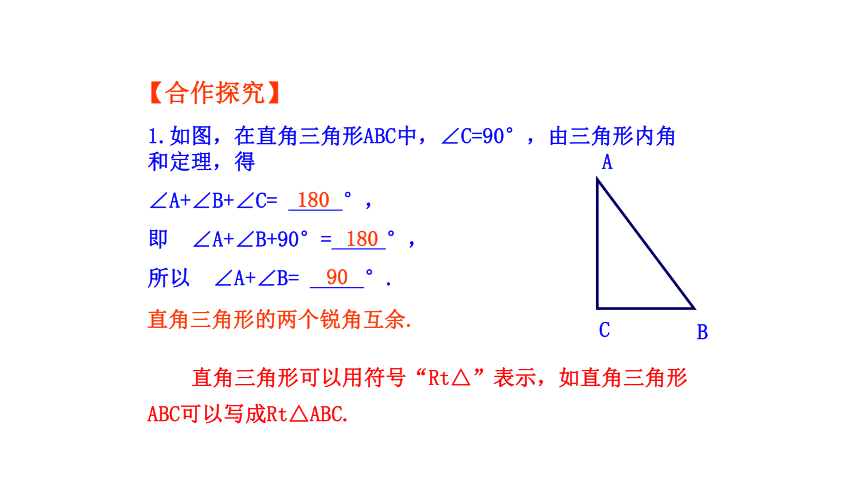
1.如图,在直角三角形ABC中,∠C=90°,由三角形内角和定理,得
∠A+∠B+∠C= °,
即 ∠A+∠B+90°= °,
所以 ∠A+∠B= °.
A
B
C
180
180
90
【合作探究】
直角三角形的两个锐角互余.
直角三角形可以用符号“Rt△”表示,如直角三角形ABC可以写成Rt△ABC.
2.如图,在△ABC中,∠A+∠B=90°,由三角形内角和定理,
得∠A+∠B+∠C= °,
即 ∠C +90°= °,
所以 ∠C = °,
所以△ABC是______三角形.
A
B
C
180
180
90
有两个角互余的三角形是直角三角形.
直角
A
B
C
D
三角形的一边与另一边的延长线所组成的角,叫作三角形的外角.
2.三角形的一个外角等于与它不相邻的两个内角的和.
1.三角形的一个外角与它相邻的内角互补.
三角形的外角与内角的关系
【例题1】
B
【跟踪训练】
B
【例题2】
A
【跟踪训练】
B
【例题3】
C
【跟踪训练】
【答案】B
三角形
按角分
锐角三角形
直角三角形
钝角三角形
按边分
三边都不相等的三角形
三角形的分类
等腰三角形
底边和腰不相等的等腰三角形
等边三角形
三边都不相等的三角形
等腰三角形
等边三角形
1.【广西百色中考】三角形的内角和等于 ( )
A.90° B.180°
C.270° D.360°
2.一个三角形的三个内角的度数之比为1∶2∶3,则这个三角形一定是 ( )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.等腰直角三角形
B
B
75°
4.如图,在△ABC中,BD,CD分别为∠ABC和∠ACB的平分线.若∠BDC=110°,则∠BAC的度数为________.
40°
5.将一副三角板如图叠放,则图中∠α的度数为________.
15°
6.如图,直线a∥b,则∠A的度数是________.
39°
7.如图所示,在△ABC中,∠ABC的平分线与∠ACB的外角的平分线相交于点D.试猜想∠D与∠A的大小关系,并说明理由.
8.如图,将△ABC沿DE,HG,EF翻折,三个顶点均落在点O处,若∠1=131°,则∠2的度数为 ( )
A.49°
B.50°
C.51°
D.52°
A
9.【核心素养题】如图,在△ABC中,∠A=64°,∠ABC与∠ACD的平分线交于点A1,得∠A1;∠A1BC与∠A1CD的平分线相交于点A2,得∠A2;…;∠An-1BC与∠An-1CD的平分线交于点An,要使∠An的度数为整数,则n的最大值为 ( )
A.4 B.5
C.6 D.7
C
10.【黑龙江哈尔滨中考】在△ABC中,∠A=50°,∠B=30°,点D在AB边上,连接CD,若△ACD为直角三角形,则∠BCD的度数为______________.
11.如图,将△ABC沿着DE对折,点A落到A′处,若∠BDA′+∠CEA′=70°,则∠A=________.
60°或10°
35°
伟人之所以伟大,是因为他与别人共处逆境时,别人失去了信心,他却下决心实现自己的目标。
2.1 三角形
第3课时
在一个直角三角形里住着三个内角,平时,它们三兄弟非常团结.可是有一天,老二突然不高兴,发起脾气来,它指着老大说:“你凭什么度数最大,我也要和你一样大!”“不行啊!”老大说:“这是不可能的,否则,我们这个家就再也围不起来了……”“为什么?” 老二很纳闷.
同学们,你们知道其中的道理吗?
内角三兄弟之争
三角形的三个内角和是多少
把三个角拼在一起试试看
你有什么办法可以验证呢
从刚才拼角的过程你能想出证明的办法吗
1.了解三角形的内角和的验证及证明过程;
2.熟练利用三角形的内角和及直角三角形两锐角的
关系解决问题;
3.知道添加辅助线是帮助解决数学问题的常用方法.
C
B
A
三角形内角和定理:三角形的内角和等于180°
已知△ABC,求证:∠A+∠B+∠C=180°
证法1:过A作EF∥BC,
所以∠B=∠2,
(两直线平行,内错角相等)
∠C=∠1.
(两直线平行,内错角相等)
又因为∠2+∠1+∠BAC=180°,
所以∠B+∠C+∠BAC=180°.
F
2
1
E
C
B
A
证法2:延长BC到D,过C作CE∥BA,
所以 ∠A=∠1,(两直线平行,内错角相等)
∠B=∠2.(两直线平行,同位角相等)
又因为∠1+∠2+∠ACB=180°,
所以∠A+∠B+∠ACB=180°.
2
1
E
D
C
B
A
证法3:过A作AE∥BC,
所以∠B=∠BAE,
(两直线平行,内错角相等)
∠EAB+∠BAC+∠C=180°,
(两直线平行,同旁内角互补)
所以∠B+∠C+∠BAC=180°.
C
B
E
A
在这里,为了证明的需要,在原来的图形上添加的线叫作辅助线. 辅助线通常画成虚线.
为了证明三个角的和为180°,转化为一个平角或同旁内角互补,这种转化思想是数学中的常用方法.
【例1】在△ABC中, ∠A :∠B:∠C=2:2:4,求∠A,∠B, ∠C的度数.
解:设每一份角为x°,则∠A=2x°,∠B=2x°, ∠C=4x° ,由三角形内角和定理,可得:
2x+2x+4x=180,
解得 x=22.5,
2x=2×22.5=45, 4x=4×22.5=90.
答: ∠A 为45°,∠B为45°, ∠C为90°.
【例题】
(1)在△ABC中,∠A=55°,
∠ B=43°,则∠ACB= ,
∠ACD=______.
(2)在△ABC中,∠A=80°,
∠B=∠C , 则∠C=____.
82°
C
B
A
D
98°
50°
【跟踪训练】
1.如图,在直角三角形ABC中,∠C=90°,由三角形内角和定理,得
∠A+∠B+∠C= °,
即 ∠A+∠B+90°= °,
所以 ∠A+∠B= °.
A
B
C
180
180
90
【合作探究】
直角三角形的两个锐角互余.
直角三角形可以用符号“Rt△”表示,如直角三角形ABC可以写成Rt△ABC.
2.如图,在△ABC中,∠A+∠B=90°,由三角形内角和定理,
得∠A+∠B+∠C= °,
即 ∠C +90°= °,
所以 ∠C = °,
所以△ABC是______三角形.
A
B
C
180
180
90
有两个角互余的三角形是直角三角形.
直角
A
B
C
D
三角形的一边与另一边的延长线所组成的角,叫作三角形的外角.
2.三角形的一个外角等于与它不相邻的两个内角的和.
1.三角形的一个外角与它相邻的内角互补.
三角形的外角与内角的关系
【例题1】
B
【跟踪训练】
B
【例题2】
A
【跟踪训练】
B
【例题3】
C
【跟踪训练】
【答案】B
三角形
按角分
锐角三角形
直角三角形
钝角三角形
按边分
三边都不相等的三角形
三角形的分类
等腰三角形
底边和腰不相等的等腰三角形
等边三角形
三边都不相等的三角形
等腰三角形
等边三角形
1.【广西百色中考】三角形的内角和等于 ( )
A.90° B.180°
C.270° D.360°
2.一个三角形的三个内角的度数之比为1∶2∶3,则这个三角形一定是 ( )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.等腰直角三角形
B
B
75°
4.如图,在△ABC中,BD,CD分别为∠ABC和∠ACB的平分线.若∠BDC=110°,则∠BAC的度数为________.
40°
5.将一副三角板如图叠放,则图中∠α的度数为________.
15°
6.如图,直线a∥b,则∠A的度数是________.
39°
7.如图所示,在△ABC中,∠ABC的平分线与∠ACB的外角的平分线相交于点D.试猜想∠D与∠A的大小关系,并说明理由.
8.如图,将△ABC沿DE,HG,EF翻折,三个顶点均落在点O处,若∠1=131°,则∠2的度数为 ( )
A.49°
B.50°
C.51°
D.52°
A
9.【核心素养题】如图,在△ABC中,∠A=64°,∠ABC与∠ACD的平分线交于点A1,得∠A1;∠A1BC与∠A1CD的平分线相交于点A2,得∠A2;…;∠An-1BC与∠An-1CD的平分线交于点An,要使∠An的度数为整数,则n的最大值为 ( )
A.4 B.5
C.6 D.7
C
10.【黑龙江哈尔滨中考】在△ABC中,∠A=50°,∠B=30°,点D在AB边上,连接CD,若△ACD为直角三角形,则∠BCD的度数为______________.
11.如图,将△ABC沿着DE对折,点A落到A′处,若∠BDA′+∠CEA′=70°,则∠A=________.
60°或10°
35°
伟人之所以伟大,是因为他与别人共处逆境时,别人失去了信心,他却下决心实现自己的目标。
同课章节目录
